不等式证明里的运算技巧*

●

(咸阳师范学院课程研究中心，陕西 咸阳 712000)

不等式是中学数学的重要内容，不等式的性质是不等式的核心知识，诸如同向不等式相加、相乘的性质等.笔者思考的问题是：异向不等式相加、相乘与同向不等式相减、相除，可以获得怎样的不等式呢？本文通过实际例子探究这个问题.

1 两个不等式相加

两个同向不等式可以叠加，产生第3个不等式.而两个异向不等式的两边是不可以进行相加推理的，但有时两个异向不等式的两边相加，选择一个不等号的方向，可能产生一个新颖的正确的不等式，这是一件十分有趣的事情，它可以帮助我们去探究、发现一些不等式的加强.

例1设a,b>0，求证：

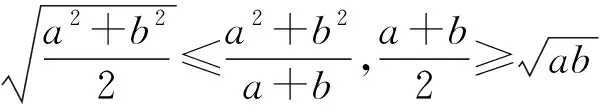
证明待证不等式

⟺

⟺

⟺

只要证明

⟺

⟺

⟺

得证.

说明十分有趣的是：两个异向的不等式的两边分别相加，选择一个不等号的方向，有时可以获得一个正确的不等式，有时获得的不等式是错误的，这就需要读者深入探究、举反例、修改和论证.

我们知道：若a,b,c>0，则有常见不等式

将这两个异向不等式相加，得到：若a,b,c>0，则：

这就说明，一些错误的做法里蕴含着正确的成分，需要人们去关注、去挖掘.又如：已知a,b,c是正实数，求证：

2 两个不等式相减

对于两个同向的不等式，将不等式的两边分别相减，获得的不等式是否正确需要论证.若是正确的，则获得了一个十分有用的局部不等式，这也为一些不等式的证明提供了一种有效的可能通道.

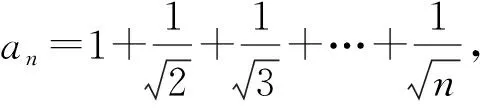
探究由待证不等式

得

将这两个同向不等式相减，得

(1)

下面证明不等式(1)成立，它是证明本题的一个有用的局部不等式.

事实上，

即不等式(1)成立.取k=1,2,3,…,n,得到n个不等式，叠加立知待证不等式成立.

说明从要证不等式得出一个不等式，并把两个同向的不等式相减，产生的不等式可能是错误的，也可能是正确的，这需要举反例或论证之.先猜后证是数学解题分析、解题思维的有效途径之一，从自己已有的知识经验出发，思考并获得一个有用的局部不等式，有时显得尤为重要.

(2)

即

用导数方法，容易证明此不等式成立，即式(2)成立.取k=1,2,…,n，得到n个不等式，叠加立知待证不等式成立.

当然，在具体的解题中，探究发现局部不等式的过程可以隐藏，不让其出现.

3 两个不等式相乘

对于两边均为正值的两个异向不等式，把它们的两边分别相乘，选择一个不等号方向，也许可以产生一个新颖有趣的正确不等式，它可能是一个常见经典不等式的加强.

例3设a,b,c>0,求证：

探究对a,b,c>0,熟知的不等式有

a3+b3+c3≥3abc，

ab+bc+ca≤a2+b2+c2.

将这两个异向不等式相乘，可得

(a3+b3+c3)(ab+bc+ca)≥3abc(a2b2+c2),

变形得

这是《数学教学》2012年第10期问题869，稍作加强，就有上述不等式.

证明待证不等式

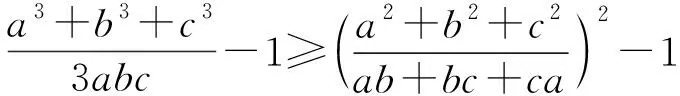
因为a2+b2+c2≥ab+bc+ca,所以只要证明

即 (a+b+c) (ab+bc+ca)2≥

3abc(a2+b2+c2+ab+bc+ca).

(3)

事实上，应用二元均值不等式，得

(ab+bc+ca)2=

(ab)2+(bc)2+(ca)2+2abc(a+b+c)≥

ab·bc+bc·ca+ca·ab+2abc(a+b+c)=

3abc(a+b+c),

从而(a+b+c)(ab+bc+ca)2≥3abc(a+b+c)2,

即不等式(3)获得证明，于是所要证明的不等式成立.

说明应用“异向不等式相乘”的方法，通过对接、调整、探究、修改和证明，有时可加强一些常见的经典不等式，获得某些新颖的不等式.

4 两个不等式相除

对于两边均是正值的两个同向不等式，把它们的两边分别相除，也许可以产生一个正确且有用的局部不等式，据此容易证明所给的不等式.

例4[2]已知n∈N+，求证：

探究由待证不等式

得

将这两个不等式相除，得

(4)

下面证明不等式(4)成立.事实上,

取k=1,2,…,n,得到n个同向不等式，叠乘即有

说明将两个同向不等式相除，获得的局部不等式可能是正确的，也可能是错误的，这就需要判断或论证，这样产生的局部不等式为证明目标不等式起到了关键作用.例4等价于1985年上海市数学高考试题第8题：对于一切大于1的自然数n，证明：

联想到2012年的一道IMO不等式赛题：设n≥3,正数a2,a3,…,an满足a2a3…an=1,求证：

(a2+1)2(a3+1)3…(an+1)n>nn.

可以试一试“同向不等式相除”研究该赛题.由待证不等式

(a2+1)2(a3+1)3…(ak+1)k>kk,

得(a2+1)2(a3+1)3…(ak-1+1)k-1>(k-1)k-1,

这两个同向不等式相除，得

(5)

这个显然是不对的，因为式(5)的左边有字母ak,而右边没有.事实上，

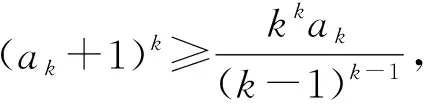
(6)

显然，不等式(6)是不等式(5)的修正.由式(6)即有

以上笔者通过具体的例子探究了不等式证明里的“加、减、乘、除”运算技巧，它可以帮助我们找到证明不等式的局部不等式或获得一个已知不等式的加强结果，更多的例子留给有兴趣的读者去探究、寻找和发现.

在“错误”的做法里寻找正确的因素有时可以发现新的不等式，找到对证明不等式有用的“局部不等式”，这也是笔者的一点经验积累，通过本文希望给读者提供一些思维的启示.