上下文敏感的复杂事件预测方法研究
2018-09-07耿少峰王永恒李仁发宋秉华郭晓曦
耿少峰,王永恒,李仁发,张 佳,宋秉华 ,郭晓曦
1(湖南大学 信息科学与工程学院,长沙 410082) 2(集美大学 计算机工程学院,福建 厦门 361021) 3(湖南大学 工商管理学院,长沙 410082) E-mail:sfgeng@163.com
1 引 言
近年来,随着信息物理融合系统(Cyber Physical System,CPS)的广泛应用,如何有效的实时处理CPS应用中所产生的大量且种类不同的数据是人们当前面对的主要问题.复杂事件处理(Complex Events Processing,CEP)[1-3]是大数据流实时处理中的一种重要技术.在CPS应用中,由各种各样的设备直接生成的数据称为原始事件.一般情况下原始事件中的语义信息非常有限,并不能直接交由高层系统来处理.CEP可以根据一些模型(如有限自动机模型、有向图模型、Petri网模型和匹配树模型等)实时的将这些数量巨大的简单原始事件进行解释和结合,从中得到有价值的高层次复杂事件.
基于复杂事件数据的预测分析(Predictive Analytics,PA)能够对获取的复杂事件建立预测模型,然后根据历史事件数据对被观测系统的某些属性进行预测,对CPS应用有着非常重要的意义.近年来贝叶斯网络[8-10]和神经网络(特别是深度神经网络)在预测模型中占据重要位置.其中贝叶斯网络及其变种能够很好的融合领域知识和数据,支持不完整数据的处理及因果分析.
目前复杂事件处理和预测分析的融合还面临着一些挑战.首先传统的分析预测方法大多是应用在数据库领域,这意味着所有的数据在任何时刻都是可用的.但在CEP中,系统只能处理单次传递的数据,无法控制随时间到达的样本的顺序.其次,一个固定的模型无法在不同的环境下都具备良好的预测性能[4].混合模型方法在一定程度上能够避免在环境变化时出现糟糕的预测结果.但模型组合方法无法确保在各种环境下能够得到最好的结果.另外随着CPS和移动计算技术的发展,多种环境的上下文信息都能够实时获取.但现有的预测方法往往只能根据有限的信息进行预测,并没有综合考虑各种实时的上下文信息.
针对上述问题,本文提出了一种以面向CPS不确定性事件流的复杂事件处理技术[13]为基础的上下文敏感预测方法(Context-aware Prediction Method for Complex Event,CPMCE).该方法将经过复杂事件处理后的数据通过上下文聚类进行划分,针对不同的数据学习对应的贝叶斯网络模型,可实现根据上下文来选择合适的模型或模型组合进行预测.
2 系统架构
2.1 总体结构
系统总体结构如图1所示.原始数据流经过概率复杂事件处理引擎的处理,从而得到有意义的高层复杂事件[13].其中PEPA(Probabilistic Event Processing Agent)为概率事件处理器[16],它负责处理由底层设备产生的原始数据流,然后生成概率复杂事件并把他们保存在历史数据库中.模型学习时首先对历史数据按时间片进行划分,然后以时间片为单位,根据事件上下文进行聚类,对每个获得的聚簇分别学习对应的贝叶斯网络结构和参数.在实时预测时,根据当前上下文适应性选取贝叶斯网络模型或模型组合进行预测.
2.2 复杂事件处理和事件上下文
CEP中的事件类型由一组具有相同语义和结构的事件规则构成.每个事件对象都是一个事件类型的实例.一个事件类型可以表示为原始事件或复杂事件.原始事件可以用三元组
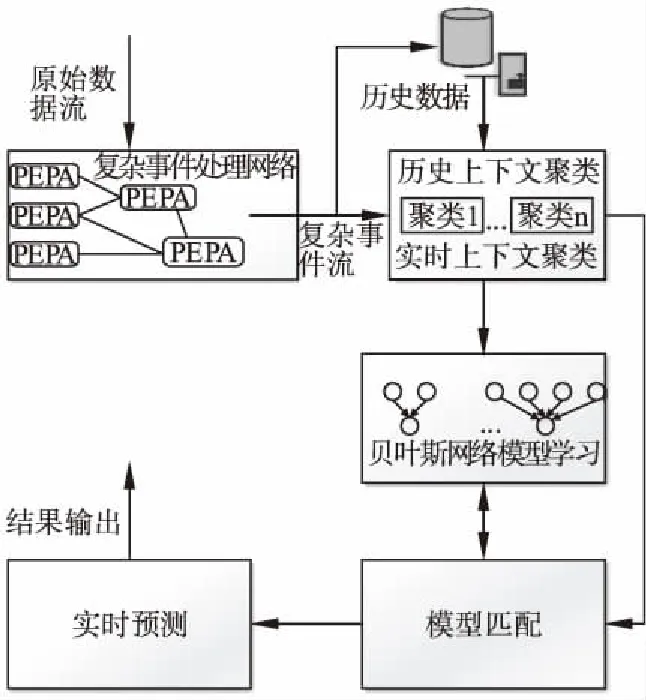
图1 系统架构Fig.1 System architecture
在事件处理领域,上下文可以定义为一些特殊的条件,根据这些条件对事件实例进行划分,并进行关联处理.事件上下文有多种类型,例如“车辆A周围1公里范围发生的事件”是一个距离上下文,“1号公路上车辆的行驶状态为缓慢”是一个状态上下文.上下文的获取一般有两种形式.一种是简单上下文,可以直接通过事件的属性来获取,另外一种是复杂上下文,需要通过定义复杂事件来获取.现实世界中上下文的表示往往是模糊的.例如“一辆行驶速度很快的蓝色的轿车”,其中“速度很快”、“蓝色”和“轿车”都是模糊的概念.本文采用模糊本体的方法对上下文建模[5].
3 状态预测
3.1 事件上下文聚类
对于同种类型的事件数据,当系统处于不同上下文状态时,数据可能符合不同的模型.上下文的聚类方法可以对事件进行划分,为不同的事件匹配合适的模型.传统的FCM算法要求事先确定聚类类别数,然而在某些应用环境中(例如道路交通领域),事先很难确定上下文聚类的种类个数,如果类别数目给定不准确,则算法会产生误导,也就破坏了算法的无监督性和自适应性.本文采用改进的FCM算法:首先由快速搜索查找密度峰值聚类算法(Clutering by fast search and find of density peaks,CSFDP)[6]确定聚类中心,然后结合FCM对历史数据进行上下文聚类.
待聚类的上下文数据集S={x1,x2,…,xn},对于S中的任何一个数据点xi,可以为其定义两个量:局部密度ρi和距离δi.
1)局部密度ρi:包括截断内核(Cut-off kernel)和高斯内核(Gaussian kernel)两种计算方式.
•截断内核:
(1)
其中,x(x)定义为:

(2)
dij表示数据点xi和xj之间的距离,dc为截断距离,需要事先指定.由公式(1)可知,ρi表示的是S中与xi间距离小于dc的数据点的个数.上下文表示的模糊本体是一个层次结构,数据点间的距离基于他们在层次结构中的距离进行定义:
(3)
其中αi和αj分别是两个上下文Ci和Cj的权值,Oij是两者之间在本体层次结构中的距离.一个事件可以对应多个上下文,为了对事件上下文集合进行距离比较,设事件x的上下文为Cx=(cx1,…,cxm),事件y的上下文为Cy=(cy1,…,cym),首先对每个cxi∈Cx,找到cyj满足minCyi(D(Cxi,Cyj)).然后Cx到Cy的距离可定义为:
(4)
其中r函数为距离的权值,同样Cy到Cx的距离为:
(5)
最后可以得到Cx到Cy的距离:
(6)
•高斯内核:
(7)
高斯内核是类似于谱聚类中的高斯核函数的形式,在谱聚类中,高斯核函数一般用来计算两个点之间的相似度.高斯内核的引入,很显然考虑到了1个数据点与所有数据点之间的关系来决定其密度.相对于截断内核,高斯内核产生冲突(即不同的数据点具有相同的局部密度值)的概率更小,这样提高了整个聚类的鲁棒性.
2) 最小距离δi:
设{q1,q2,…,qn}是表示{ρ1,ρ2,…,ρn}的一个降序排列下标序,则距离可定义为:
(8)
由公式(8)可知,当点xi具有最大局部密度时,δi表示S中和xi距离最大的数据点与xi间的距离;否则,δi表示在所有局部密度大于xi的数据点中,与xi距离最小的那个数据点与xi间的距离.其中那些密度和距离相对比较大的数据点被其它点围绕着.
对于S中的每一个数据点计算出其(ρi,δi)的值,然后按照ρ为横轴,δ为纵轴的方式将所有的数据点标识在一张二维决策图上.找出其中具有较大密度值和距离值的数据点作为S的初始聚类中心.由此确定的初始聚类中心采用的是定性分析,且具有主观因素,所以未必是最优结果.接下来根据初始聚类中心和历史数据,通过迭代过程修正聚类中心,寻找使以下目标函数取得最小值的结果:
(9)
其中V=[V1,…,Vc]为聚类中心,uij表示了第j个数据对第i类的隶属度,m是一个取值范围为[1,+)的模糊加权指数,用来控制隶属度矩阵U=[μij]c×n的模糊程度.表示第i个聚类中心与第j个数据点之间的距离.
用拉格朗日乘法求解公式(9),构造目标函数:
(10)
λj(j=1,2,…,n)是n个约束式的拉格朗日乘子,对输入参量求导,使公式(9)达到最小的必要条件为:
(11)
(12)
根据公式(11)和公式(12)对每一次迭代后的聚类中心以及隶属矩阵进行适当的调整,当相邻两次的聚类中心之间的变化小于预先设定的阈值ε时,则可判定该算法收敛,即得到了最佳的聚类中心和隶属矩阵.
3.2 基本预测方法
CPS应用中,不同传感器产生的事件可能适合不同的模型,甚至同类型的事件在上下文不同时也可能适用不同的模型.针对这个问题,在获得上下文聚类相关情况的基础上,CPMCE采用一种适应性贝叶斯网络模型(Appropriate Bayesian Network,ABN)来提高预测的准确度.
ABN模型实例如图2所示.其中包括一个状态平面和一系列位置平面.每个平面是一个包括时间和空间两维贝叶斯网络.在状态平面中,结点代表不同时间和空间的对象位置聚集或流量的状态(例如某个路口车辆的拥堵状态),边代表状态之间的条件概率.针对CPS应用中贝叶斯网络结构经常变化的情况,引入适应性贝叶斯网络,其中的“适应性”是指贝叶斯网络的实际结构可通过学习历史数据得到,并可在数据变化时进行调整.每个对象位置平面代表对象在不同时间的位置及位置转换的概率.在某个时间段内物体移动的位置链就构成了物体的移动路径.

图2 适应性贝叶斯网络模型Fig.2 Appropriate Bayesian network model
本文将交通网络视为贝叶斯网络来分析预测其各个节点的流状态(拥堵程度).图2中节点总数为N(NT+1).其中节点(i,t)的状态受t时刻之前多个父节点影响.设fi,t表示节点i在t时刻的流状态,pn(i,t)表示贝叶斯网络中节点(i,t)的父节点的集合,NP表示pn(i,t)中节点的数量,pn(i,t)的状态集为Fpn (i,t)={fj,s:(j,s)pn(i,t)}.根据贝叶斯网络理论,网络中所有节点的联合分布可以表示为:
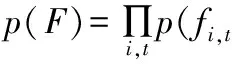
(13)
其中条件概率p(fi,t|Fpn(i,t))可以按照下面的公式计算:
p(fi,t∣Fpn(i,t))=p(fi,t∣Fpn(i,t))/p(Fpn(i,t))
(14)
将联合分布p(fi,t,Fpn(i,t))使用高斯混合模型来建模[12]:
(15)
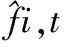
3.3 适应性贝叶斯网络学习方法
本文采用一种混合型的方法来学习及更新贝叶斯网络的结构.学习方法分两步,先用基于约束的方法,根据对数据依赖的分析构建候选集,然后用打分-搜索的方法最终确定网络结构.针对图2所示的模型特征,首先采取从位置平面数据构建状态平面结构的方法.其依据是位置平面记录了物体位置极其移动的详细信息,而这些信息决定了系统总体状态平面的结构.寻找一个节点对应的候选集的初步算法如下:
算法1.获取结点对应的候选集
输入:O为位置平面的对象集合,i为目标结点
输出:Ni为结点i对应的候选集
方法:
begin
Pi←{P|P∈O^i∈Dest(P)}
foreachp∈P
fork=1 to |p|
I[p(k)]+=α|p-k|/count(p(k))
end
end
Ni←{n|n∈N^I(n)>θ}
returnNi
end
算法描述中忽略了结点路径中的概率部分,其中Dest(P)获取平面P中所有路径的目标结点.I是一个影响因子数组,保存了每个其它结点到结点(i,t)的影响因子(通过条件概率表CPT计算).Count(n)函数获取通过结点n的的所有路径,α是一个衰减因子,θ是一个阈值.此算法在面对大量位置平面时可采用并行的方式处理数据.
接下来进行搜索-打分,其基本思路是使BIC(Bayesian Information Criterion)打分函数最大化:
(16)

3.4 多贝叶斯模型组合
由于本文之前对上下文的划分采用的是模糊聚类的方式,考虑到事件上下文的复杂性,所以允许将一个样本划分到多个聚簇中.在实时预测时,如果当前事件上下文和已有多个聚类比较接近,那么选择所有符合条件的聚簇模型,通过多贝叶斯模型组合的方法进行预测[2].这是提高预测准确度的一条有效途径.
假设有K个可能的预测模型,模型Mk有一个有mk个参数构成的参数向量Θk=(θ1k,θ2k,…,θmk),D为数据集合.根据贝叶斯公式有:
(17)
其中p(D|Mk)为模型证据,可以通过式(18)计算:
(18)
每个模型的后验概率如下计算:
(19)
其中p(Mk)代表模型Mk的先验分布,在对模型没有偏好的情况下,假设每个模型具有相同的先验概率.而p(D)与模型无关,所以不同模型的质量主要取决于p(D|Mk).公式(19)可转化为:
(20)
这是每个模型的权值.使用交叉检验分布,可以对公式(18)中的p(D|Mk)进行有效评估:
(21)
其中p(yi|Mk)为:
(22)
在模型比较复杂的情况下,可以采用马尔可夫链蒙特卡洛(Markov Chain Monte Carlo,MCMC)方法来近似计算.通过抽样从θk的分布p(θk|Mk)获得θk的一系列独立样本θk(t):t=1,…,T,则公式(22)可以用下式来近似:
(23)
MCMC方法的关键是找到独立的样本序列.采用马尔可夫链θ0,θ1,…,θn,序列的每个值只依赖于它前面的值.当满足一定的条件时,无论序列的初始值取什么,在迭代m次之后序列都将收敛于目标静态分布p().那么随后的迭代生成的样本θ(t):t=m+1,…,n就可以作为MCMC的独立样本.
4 实验结果与分析
本文实验选取了两种事件源:真实应用数据和交通模拟系统.真实应用数据来自洛杉矶101公路的PeMS交通监视网络,它可以采集各种不同时间间隔的实时交通流数据,主要包括交通流量(flow)、速度(speed)和占有率(Occupancy)等[15].这些真实应用数据中的交通网络和事件的上下文比较简单,因此本文还采用了开源的交通模拟系统SUMO[11].实验的框架如图3所示,用JADE(Java Agent Development Framework)框架对SUMO进行扩展来支持多Agent系统,同时使用SUMO的TraCI接口来获得车辆的实时位置信息,用它们来模拟GPS阅读器.地图中设置了15×15个路口和8万辆汽车.为了更接近真实情景,定义了一组规则:每辆车都设置了家的位置和办公室位置.车辆Vi在家庭和办公室之间运行的概率是pi.这些车辆还有一定概率去其他地点.实验使用了3台至强E3处理器和16GB内存的服务器当作数据处理服务器.

图3 系统实现框架Fig.3 System implementation framework
实验中FCM的参数m取2,阈值ε取0.001,GMM中模型数M取25至30之间效果比较理想.真实应用数据选取了PeMS中I-405道路上一个观测站在2016年3月7日至2016年3月13日的交通流数据作为模型训练样本.实验选取交通状态为事件上下文,流量、速度和占有率3个参数作为交通状态评判的输入变量.对于SUMO仿真数据,首先多次运行系统,尽量使系统出现各种类型的上下文,保存历史数据并离线训练模型.
在得到真实数据和模拟数据事件上下文后,本文将CPMCE与Pascal等人采用的贝叶斯网络(BN)[9]和Huang等人采用的深度置信网络(DBN)[14]进行了对比.真实数据以30分钟为间隔进行预测,结果如图4所示.从结果中可以看出在大部分时间内,CPMCE相比其他方法有更好的准确性,但是相差不大.原因在于车流量大约在6.5小时后相对稳定,事件的上下文并没有很大改变,这使得CPMCE的优势没有完全发挥.模拟数据以1分钟为间隔进行预测,结果如图5所示.相对于真实数据,模拟数据的车流量更大,而且变化更加剧烈,此处最重要的上下文变化是自由流、同步流和阻塞流间的变化.三种方法的准确度都有所下降.但是CPMCE方法相对于BN和DBN得到了更好的结果,这是因为CPMCE针对不同的事件上下文而采用了多贝叶斯网络模型组合的方法.

图4 PeMS数据预测结果Fig.4 Prediction result for PEMS data
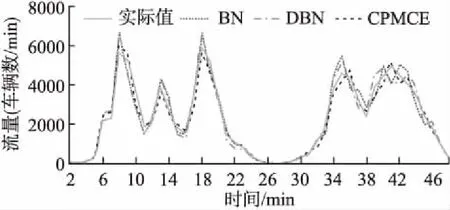
图5 SUMO数据预测结果Fig.5 Prediction result for SUMO data
5 结束语
本文提出了一种以复杂事件处理技术为基础的上下文敏感预测方法.该方法以复杂事件处理为基础,采用模糊本体对历史事件上下文进行建模,然后通过上下文聚类来实现数据的划分.针对不同的数据学习对应的贝叶斯网络模型,能够根据当前事件上下文选择合适的模型或模型组合进行预测分析.实验评估表明,本方法能有效的处理事件数据流,并具有良好的预测性能.本文还有一些不足之处,首先,上下文聚类中心的选择采用的是定性分析,缺乏一种有效的自动学习方式.其次,没有考虑并行与分布式预测处理.研究如何解决上述问题是今后工作的重点.
