改进K均值聚类算法
2018-01-11屈传慧
杨 娟,屈传慧
(西安电子科技大学,陕西 西安 710071)
改进K均值聚类算法
杨 娟,屈传慧
(西安电子科技大学,陕西 西安 710071)
K均值聚类算法因需给定聚类中心数,使得聚类结果受初始化中心数的影响很大。介绍了K均值聚类法的概念,并引入层次聚类的概念,采用先分解后合并的思想对K均值法进行了改进,对改进后算法进行了仿真验证。
K均值;聚类算法;分解合并
0 引 言
聚类,就是将样本分配到不同类的过程[1]。聚类的基础为样本之间的相异性,聚类即寻找样本之间的相似度对样本进行划分。
目前,常用的聚类方法包括:划分聚类、层次聚类、密度聚类等。划分聚类就是对给定的数据集,采用分裂法构造K个分组,每个分组就代表一个聚类,且每一个分组至少包含一个数据纪录,每个分组互不相交,即每一个数据纪录属于且仅属于一个分组,常见的算法如K 均值算法、CLARANS算法等[2]。层次聚类就是对给定的数据集进行层次分解或者合并,直到所有的记录组成1个分组或者某个条件满足为止,具体又可分为合并(自底向上)和分解(自顶向下)2种方案,常见的算法有BIRCH算法、CURE算法等[3-4]。密度聚类基于密度,它克服了基于距离的算法只能发现超球形聚类的缺点,该方法的基本思想就是只要一个区域中的点的密度大过某个阈值,就把它加到与之相近的聚类中去,其代表算法有 DBSCAN算法、OPTICS 算法等[5]。在众多的聚类方法中,K均值方法是一种最经典的也是应用最广泛的聚类方法[6-7],该方法对超球形和凸状数据有很好的聚类效果。但是,由于经典K均值算法必须在聚类前就设置聚类的个数K,最后所得到的聚类结果会受到初始选择的聚类个数的影响。若聚类个数选择得过小,可能导致同一类内的有些样本差别过大,若聚类个数选择得过多,可能导致不同类间的样本差别过小,都达不到有效聚类的目的。因此,如何选择合适的聚类个数一直是聚类问题中讨论的热点问题[8]。
本文基于K均值法,引入层次聚类的思想,对K均值法进行了改进,改善了K值的取值矛盾问题,使得改进后的算法受初始聚类个数的影响变小,有助于得到更好的聚类效果,且相比其它层次K均值聚类算法,本算法实现简单。
1 经典K-均值聚类
K均值算法能够使聚类域中的所有样品到聚类中心距离平方和最小。其原理为:先取K个初始聚类中心,计算每个样品到这K个中心的距离,找出最小距离,把样品归入最近的聚类中心,修改中心点的值为本类所有样品的均值,再计算各个样品到新的聚类中心的距离,重新归类,修改新的中心点,直到新的聚类中心和上一次聚类中心差距很小时结束。此算法结果受到聚类中心的个数和聚类中心初次选择影响,也受到样品的几个性质及排列次序的影响。如果样品的几何性质表明它们能形成几块孤立的区域,则算法一般可以收敛。
2 改进K均值聚类
K均值算法需设置聚类数,改进的K均值算法初始化K值时,设置比较大的K值,此处K值具体的设置需根据所聚类对象来设置,若无法判断,则只需将其设置很大即可,但此时的计算量也将增大。改进的K均值法采用先分后和的思想,即先将整个数据根据K均值法聚类成设置的K个集合,再利用各集合中心与其相对应的最大聚类半径确定的圆与其它圆的交叠的比例来确定是否合并,当交叠比例超过门限时,2个聚类结果合并,更新合并后的聚类结果,如此往复。直至所有的聚类结果不满足合并条件,此时的结果作为最终的聚类结果。
交叠比例的计算方法为:计算第i个聚类结果中的每个元素与第j个聚类中心的欧氏距离,欧氏距离的计算方法:
(1)
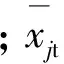
第j个聚类结果的聚类半径rj的计算方法为:
(2)
式中:i=1,2,…,K;p=1,2,…,n;j=1,2,…,K,i≠j。
当该距离小于第j个聚类半径,即dipj≥rj时,交叠值加一;否则,不加一。最终计算交叠值与第i个聚类结果数据数的比值,当比值大于门限时,合并第i个聚类结果和第j个聚类结果,作为新的聚类结果;当比值小于门限时,不合并,此文档中的门限值取为定值0.5,即当2个聚类结果有一半以上数据交叠时,将两者合并归为一类。
改进后的K均值算法流程如图1所示。
3 仿真分析
图2为聚类前的数据二维平面图,图3为K均值法的聚类结果图,图4为改进后的K均值法的聚类结果图。由仿真结果可得:改进后的算法对K均值聚类分离的7类结果进行了相似合并,最终聚类结果为3类,聚类效果较好。
4 结束语
本文对K均值聚类算法进行了改进,改进后的K均值算法对初始化时的聚类数依赖性小,且算法实现简单,并对改进后的算法进行了仿真验证,该聚类算法可用于各种无监督聚类应用中,也可以用于电子侦察中的信号分选模块。
[1] 贺玲,吴玲达,蔡益朝.数据挖掘中的聚类算法综述[J].计算机应用研究,2007,24(1):10-13.
[2] 谢崇宝,袁宏源.最优分类的模糊划分聚类改进方法[J].系统工程,1997,15(1):58-63.
[3] CILIBRASI R L,VITANYI P M B.A fast quartet tree heuristic for hierarchical clustering[J].Pattern Recognition,2011,44(3):662-677.
[4] 李凯,王兰.层次聚类的簇集成方法研究[J].计算机工程与应用,2010,46(27):120-123.
[5] 武佳薇,李雄飞,孙涛,等.邻域平衡密度聚类算法[J].计算机研究与发展,2010,47(6):1044-1052.
[6] KANUNGO T,MOUNT D M.A local search approximation algorithm for K-means clustering[J].Computational Geometry,2004,28(2/3):89-112.
[7] ELKAN C.Using the triangle inequality to accelerate K-means[C]//Proceedings of The 2nd International Conference on Machine Learning.Menlo Park:AAAI Press,2003:147-153.
[8] 胡伟.改进的层次K均值聚类算法[J].计算机应用研究,2013,49(2):157-159.
ImprovedK-meansClusteringAlgorithm
YANG Juan,QU Chuan-hui
(Xidian University,Xi'an 710071,China)
Because the K-means clustering algorithm need to give the clustering center number,the influence of initial center number on clustering result is great.This paper introduces the concept of K-means clustering algorithm and inducts hierarchical clustering concept,adopts the idea of decomposition before combination to improve the K-means algorithm,simulates and validates the improved algorithm.
K-means;clustering algorithm;decomposition and combination
2017-06-23
TN911.7
A
CN32-1413(2017)06-0091-03
10.16426/j.cnki.jcdzdk.2017.06.020
