基于八数码问题的搜索算法的研究

楚孟慧，吴姝瑶

（山东科技大学电气信息系，山东济南，250031）

0 引言

人工智能这个词已经成为现代科技前沿的的代表了。人工智能在最近几年逐渐成为互联网方向的主流，作为一种新兴的现代技术在互联网领域的多种服务上已经有所体现。其中搜索过程是人工智能技术实现的一个重要环节，是推理不可或缺的一部分。求解一个问题实质上就是对现有知识进行搜索，搜索也是求解问题的方法和过程。掌握搜索算法对人工智能的开发至关重要。

1 搜索的概括与八数码问题

搜索是如何利用知识找到问题的解并记录下求解路线或者求解过程的算法。搜索分为两种，一种是盲目搜索一种是启发式搜索。盲目搜索即在没有任何提示，或者知识的指导下，按照系统规定的规则对知识库进行搜索，无论什么问题都采用相同的搜索方式。这种搜索方式虽然适用于所有问题但当碰到复杂的问题时就需要耗费相当长的时间，效率较低，因此盲目搜索只适用于解决较为简单的搜索问题。启发式搜索是在盲目搜索的基础上不断的增加搜索信息改变搜索方向使问题得到更快的解决，提高搜索解决问题的效率的一种新的搜索方式。

八数码问题：在3＊3的棋盘上摆放着八个数码1、2、3、4、5、6、7、8有一个地方是空格，我们可以对空格进行上下左右的移动使得八数码盘从初始状态如图1转变为目标状态如图2所示。

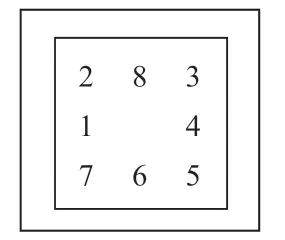
图1 初始状态

图2 目标状态

2 盲目搜索

■2.1 宽度优先搜索

宽度优先搜索策略的核心思想为从初始结点开始首先判断初始结点是否为目标结点如果为目标结点则搜索结束，若不为目标结点则遍历该结点的所有子结点并同时判断遍历的每一个子结点是否为目标结点。然后依次将每一个子结点作为初始结点完成上面的操作，直到找到目标结点。针对八数码问题给出宽度优先搜索的算法步骤如下：

a.把初始结点S0放入链表1中。

b.如果链表1是空表，则没有解，失败退出；否则继续。

c.把链表1中的第一个结点（记为结点n）移出，并放入 链表2中。

d.判断结点n是否为目标结点，如果是，则求解结束，并用回溯法找出解的路径，退出；否则继续执行e。

e.若结点n 不可扩展，转b；否则继续执行e。

f.对结点n进行扩展，将它的所有子结点放入链表1的末端，并为这些子结点设置指向父结点n的指针，然后转b。

以下是宽度优先搜索策略解决八数码问题的搜索树如图3所示。

图3中每个方块代表一个状态，每个状态左边的数字为此状态的编码，开始结点为S0首先对判断S0是否为目标结点，若S0为目标结点则该搜索过程结束，若不是则拓展S0，对于此问题来说S0并不是目标状态，于是我们拓展S0并且判断S0的子结点是否为目标结点以此作为循环直到每一层的结点扩展结束再进行下一层的判断，直到找到目标结点。目标结点为Sg经过27个结点最终到达目标结点可以看出其路径为：S0，3 , 8 , 16 , Sg。

图3 宽度优先搜索树

由图3可以看出宽度优先搜索解决八数码问题时会产生大量的无用结点。但宽度优先搜索总能找到最后的解。

■2.2 深度优先搜索

深度优先搜索的核心思想是从初始结点出发，扩展顺序总是先扩展最新产生的结点，这样搜索顺序就会顺着一条路径一直延伸下去，直到最后的结点不能产生新的结点或找到目标结点为止。当搜索到不能产生新的结点且还是无法找到目标结点时，就会沿着最终结点的反方向寻找能够产生新的结点的结点并且搜索新产生的结点，就这样执行以上步骤，直到找到目标结点或者再无可扩展结点为止。针对八数码问题给出深度优先搜索的算法步骤：

a.将初始结点S0放入链表1。

b.如果链表1为空，则问题无解并退出程序。

c.在链表1中将第一个结点（结点n）移出，放入已经扩展结点链表2中。

d.考察结点n是否为目标结点，如果是，即找到问题的解，并回溯法求解的路径然后退出。

e.若结点n不可再扩展，则转b。

f.扩展结点n，将其子结点放到链表1的前端，并为其设置指向结点n的指针，之后转b。由于过程详细此处不再展示搜索树。

深度优先搜索容易陷入某个错误的方向，在错误的分支上一去不返，造成大量的结点浪费，而且深度优先搜索并不能保证找到目标状态，容易陷入一个死循环。

3 启发式搜索

根据以上盲目搜索中它们进行的搜索路线是事先确定好的，没有根据被求解问题的任何有利信息。没有考虑现在正在搜索的路径是否更有利于接近目标结点。所以启发式搜索正是弥补了盲目搜索的这一劣势，启发式搜索在搜索过程中关键是如何确定哪一个是下一个要被判断的结点，在确定下一个需要被判断的结点时要利用有关结点能够做出判断的信息，计算出结点的重要性，并且要选择重要性高的结点来拓展。因此启发式优先搜索应定义一个估价函数f(x)，我们以八数码问题为例f(x)由两部分组成一部分是该结点所在层数计为m(x)，另一部分是该结点与目标结点中数字所处不同位置的个数计为n(x)。所以估价函数可写作：f(x)=m(x)+n(x)。例如当S0结点位于第0层时它的m(x)=0,与目标结点数字不相符的地方有3处所以n(x)=3那么f(x)=3。由f(x)的定义可知，f(x)越小说明距离目标结点越近，所以我们应首先考察和拓展f(x)值最小的点。针对八数码问题给出启发式搜索算法步骤：

a.将初始结点S0放入链表1，并计算f(S0)的值。

b.如果链表1为空链表，则问题无解并退出。

c.将链表1中第一个结点记为结点n移入链表2中。

d.考察结点n是否为目标结点，如果是，则求得问题的解并退出；否则转e。

e.若结点n可扩展，转f；否则转b。

f.对结点n进行扩展之后，并计算所有子结点的估价函数f(x)的值，并为每个子结点设置指向n的指针。

g.把这些子结点都送入链表1，然后对链表1中的全部结点按照估价值从小到大的顺序进行排序。

h.转b。

根据这些规则可以得到算法流程图如图4所示。

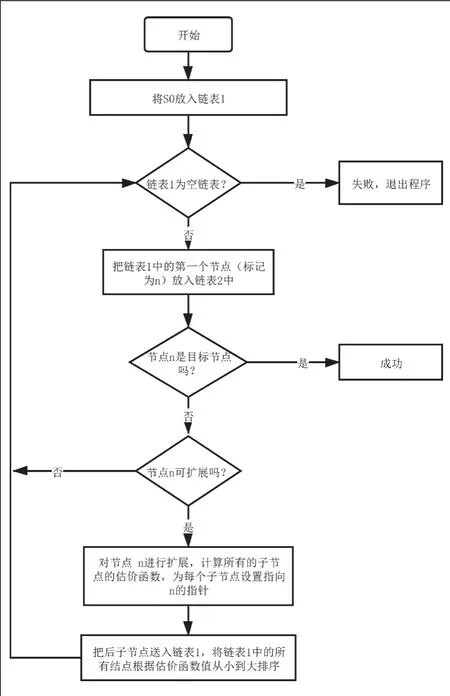
图4 启发式搜索算法流程图

根据此算法得出搜索树如图5所示。

图5中每一个方块代表一个状态，每个状态左边的数字代表估价函数的值。首先判断S0是否为目标结点，若S0为目标结点则搜索过程结束，若S0不为目标结点，则拓展S0并计算所有子结点的代价函数，取其中代价函数最小的结点进行判断，若不是目标结点则扩展此结点，并计算其子结点的代价函数，这时再次寻找没有判断过的代价函数最小的结点直到找到目标结点。由图5可知搜索的结点数目与盲目搜索相比减少了很多，经过搜索13个结点找到了目标结点并且面对更加复杂的问题时启发式搜索的效率会明显增加。

图5 启发式搜索

4 总结

现实中的问题都是通过一步一步求解得到答案的，所以人工智能也是仿造人类一步一步搜索出最终答案。盲目搜索在不加入任何特征信息时进行搜索，这种搜索类似于没有方法但知道答案的范围将答案带入问题去匹配，只有少数问题能够比较幸运的快速算出，大多数较为复杂的问题在进行搜索时就会耗费大量内存。启发式搜索就像得到了解决问题的方案，每走一步都是距离目标更近的一步，对于复杂的问题往往能快速找到解决方案。因此掌握启发式搜索技术对于研究人工智能领域有着重要意义。