一种卷积神经网络的稀疏性Dropout正则化方法
2018-09-07周安众
周安众,罗 可
(长沙理工大学 计算机与通信工程学院,长沙 410114) E-mail:sprite4@163.com
1 引 言
卷积神经网络模型拥有大量的可训练参数,使其具有强大的特征提取能力,在机器学习领域表现优异[1].并且通过增加网络层数和卷积核数量可以进一步提升其性能[2].然而随着层数和卷积核数的增加,模型变得更加复杂,大量参数的学习受限于训练数据的规模,当训练数据不足时,常常出现过拟合现象,导致模型泛化能力变差.怎样减小过拟合问题的影响就成为了近年来在卷积神经网络中急需解决的一个问题.
在实际应用中,组合多个模型几乎总可以获得比单一模型更好的结果.但是对于越来越复杂的卷积神经网络,训练多个模型变得越来越困难.为了降低模型的复杂度,又不影响特征表达能力,常用的方法是对参数施加额外限制,间接减少自由变量的参数数量,称为正则化方法[3].L2正则化[4]是其中一种简单且有效的方法,在权值优化过程中使模型倾向于选择较小的参数,避免过大参数的影响.Hinton等[5]提出的Dropout是另外一种正则化方法,在网络对不同的样本进行训练时以一定概率随机将部分节点的输出值置0,相当于将此节点从网络中删除,每个样本只训练原网络的一部分,测试时再组合所有部分形成完整的网络.该方法在机器学习的许多问题中都取得了不错的效果.DropConnect[6]采用类似的方法,通过随机删除部分连接权值可以从原网络中得到更多的局部结构,最后通过组合所有部分取得了更好的结果.
Dropout用固定的概率随机从原网络中删除部分节点,由于每个节点被删除的概率相等,保留下的网络结构对所有样本服从统一分布,没有对不同样本进行区分,都具有同等的特征提取能力.基于这种想法,本文希望局部结构对样本的特征是敏感的,根据文献[7],神经网络对不同的刺激是有选择性激活的,如颜色、材质、边缘等,只提取自己感兴趣的部分,相当于从原始的稠密数据中分离出关键特征数据.这个特点使神经网络表现出稀疏性,对特征感兴趣的节点有较大的激活值,不感兴趣的节点激活值为0或者接近于0.因此,需要保留对特征感兴趣的节点以提高模型的判别性.
基于以上讨论,本文提出一种稀疏性Dropout(Sparse Dropout,S-Dropout)正则化方法,其基本思想是更改局部结构对样本的统一分布,寻找对特征感兴趣的节点.为此,在Dropout的基础上增加稀疏性限制,训练时以更大的概率删除激活值较低的节点.通过该方法训练的卷积神经网络不仅组合了多个局部结构,同时利用稀疏性提高了每个局部结构的特征提取能力,使模型的泛化能力得到提升.
2 相关基础
2.1 Dropout正则化方法
2012年文献[5]提出了Dropout正则化方法,在神经网络中得到了广泛应用,能有效防止模型过拟合问题.该方法在神经网络的训练阶段,前向传播时以概率P=0.5随机删除掉部分节点,这样网络在传播时只会通过保留下的节点,如图1所示,相当于从原网络中随机选出一个局部结构.
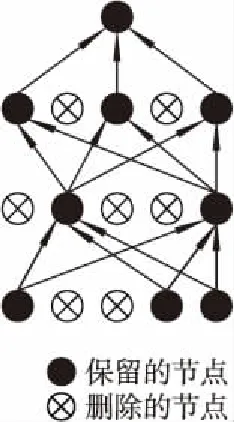
图1 使用Dropout正则化训练时的网络结构Fig.1 Use dropout to regularize the structure of the network during training
训练过程中删除节点的方法是强制将此节点的激活值置0,此时节点在网络中没有任何贡献,误差也不会经过输出值为0的节点反向传播.节点激活值的计算如公式(1)所示:
r=m·f(wx+b)
mj~Bernoulli(p)
(1)
公式(1)中x是输入,f是激活函数,m是一个二值掩膜矩阵,m中的元素mj以伯努利概率P随机取值0或1.每个节点激活后乘以m中对应元素得到最后的输出值r,mj为1的对应节点输出值保留下来,mj为0的对应节点输出值为0.
在测试阶段,将删除的节点恢复以组合所有的局部网络,此时网络结构的改变使总的输出值发生改变,如图2所示,为了保证输出值不变,测试阶段的节点激活值需要乘以一个比例系数,即节点被删除的概率P,相当于对所有局部网络取平均值.

图2 训练阶段与测试阶段节点的输出值Fig.2 Output value of the training phase and the test phase node
此方法的优点是随机产生的局部网络拥有比原网络更少的参数,不容易过拟合,而且每次产生的局部网络的参数共享自原网络的一部分,虽然总的网络个数增加了,但是参数没有增加,在没有提升训练难度的情况下可以得到多个网络的训练结果,测试时再组合这些局部网络,使泛化性得到提升.另一方面,神经网络的节点之间有相互合作能力,这种合作能力很容易拟合到一些噪声,随机的选择节点打破了合作表达的联系,能有效防止模型的过拟合问题.
2.2 神经网络的稀疏性
自从Olshausen等[8]发现自然图像具有稀疏结构,大量研究关注于稀疏编码和稀疏特征表示[9,10],用于解决机器学习中的各项任务.当前深度学习中一个明确的目标是从数据中提取出关键特征.大量的训练样本富含稠密的信息,其中可能包含着大小不同的关键特征,假如神经网络具有稀疏性,可以将稠密特征转换为稀疏特征,就具有更强的鲁棒性.Bouthillier等[11]通过分析Dropout正则化方法,指出局部空间特征有更好的区分性,将数据映射为特征后,特征之间的重叠度越低越好,而降低重叠度的主要方法就是使特征产生稀疏性,稀疏特征有更大可能线性可分,或者对非线性映射机制有更小的依赖.Wan等[6]将神经网络激活值二值化后也能得到不错的效果,不仅说明了稀疏性的正确性,同时表明激活值不是最重要的,重要的是节点是否被激活,当一个节点被激活时,表示该特征存在于一个子空间中,模型重点关注子空间中的特征.线性修正单元激活函数(Rectified Linear Units,ReLU)[12]正是利用了稀疏性的特点,将小于0的激活值置0,在深度神经网络中被大量采用.
3 稀疏性Dropout正则化方法
为了利用Dropout组合多个模型的能力,同时使模型对局部关键特征有更好的表达能力,本文受稀疏自编码器的启发,对节点激活值增加稀疏性限制,提出S-Dropout正则化方法.根据激活值的大小选择节点,使更多激活值较低的节点输出值为0,相当于将这部分节点从网络中删除,而不再采用Dropout中所有节点都以相等的概率被删除的方式.对模型中的某一层施加稀疏性限制时,取这一层所有节点激活值的中值,大于中值的定义为高激活值节点,小于中值的定义为低激活值节点.高激活值的节点代表网络对样本感兴趣的部分,对分类结果起到关键作用,是主要保留的节点.然而对于激活值小的那部分节点并不是完全没有作用.Ngiam等[13]的研究发现,在样本空间不足的情况下,需要通过全局训练样本的共同作用才足以表达出测试样本.Sun等[14]依据节点之间的相关性对网络进行裁剪,指出相关性接近0的弱相关节点对相关性高的节点有补充作用,可以提高分类结果.基于此,为了进一步提升模型的表达能力,增加一个随机因素,保留一部分低激活值节点.首先考虑S-Dropout在全连接层上的应用,如图3所示,模型随机保留大部分高激活值的节点,同时随机选择小部分低激活值节点保留,稀疏化的模型使得分类能力提高,而随机性的加入使模型有更强的鲁棒性[15].
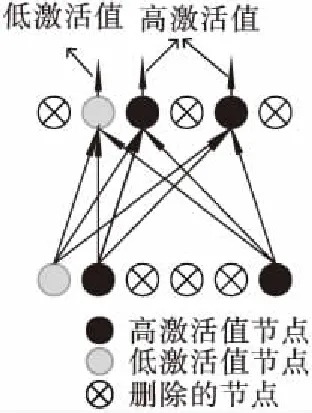
图3 使用稀疏性Dropout训练时的网络结构Fig.3 Use sparse dropout to regularize the structure of the network during training
根据上述讨论,S-Dropout正则化方法定义了两个参数需要优化,稀疏度S和随机因素λ,S(0 S|r|=(1-λ)S|rm+|+λS|rm-| (2) |r|代表一层中节点的数量,|rm+|和|rm-|分别代表高激活值节点和低激活值节点数量.本文中S取0.5,λ取0.7,实验部分分析取值原因.于是在训练阶段全连接层将删除50%的节点,其中的70%为低激活值节点,30%为高激活值节点.节点的激活值计算公式同公式(1),不同的是掩膜矩阵的表示,如公式(3)所示. r=m·f(wx+b) (3) 由于每个节点被删除的概率不再相等,测试阶段组合所有局部网络时,不能简单地采用2.1节Dropout的方法乘以概率P.此时,为了达到类似Dropout平均局部网络的目的,测试阶段激活值需要乘以一个比例系数α,使得测试阶段激活值总和与训练阶段激活值的期望相等,计算方法如公式(4)、公式(5)所示. (4) (5) 公式(4)中E[r]是训练时S-Dropout层激活值的期望,由高激活值节点和低激活值节点的期望相加得到,然后根据公式(5)计算期望与激活值总和的比值α,最后测试阶段的节点激活值乘以α得到输出值. 将稀疏性限制应用在卷积层时与全连接层遵循一样的流程,不同的是计算各项参数时不再是针对整个层的节点,而是根据每一个卷积层的各个特征图分别计算.对于一个特征图,首先找到特征图中所有节点激活值的中值,然后根据中值找出特征图中的高激活值节点和低激活值节点,最后,同样根据公式(4)、公式(5)计算训练阶段和测试阶段的激活值.图4给出了整个算法的流程. 图4 稀疏性Dropout正则化的计算流程 通过对Dropout增加稀疏性限制,卷积神经网络每次迭代训练时的结构都不相同,而每次结构的改变都使部分节点有选择地激活,相当于产生了不同的激活路径,路径上的节点只对特定样本敏感,去除了不相关因素的干扰,使得卷积神经网络成为一个大小可变的容器,处理不同的样本变得更加灵活.另一方面,对于难以求得的全局最优解,从多个容易求得的局部解去逼近,这也是正则化思想的体现,可以更好地从有效的数据维度上,学习到相对稀疏的特征,起到自动提取关键特征的效果. 为了对比本文方法在卷积神经网络上的效果,使用L2、Dropout、S-Dropout正则化方法分别在MNIST[16],CIFAR-10/100[17]数据集上进行比较.根据不同的数据集,实验使用的卷积神经网络略有不同,以下几点是共同使用的相同策略: 1)训练采用随机梯度下降算法,每个样本都进行了预处理,减去所有样本的均值. 2)所有卷积层和全连接层都使用ReLU激活函数,且卷积层后都有池化层进行降采样. 3)训练使用标准数据集中的数据,没有进行数据扩充. 4)权值参数采用均值为0,方差为1的高斯分布随机初始化,由于Dropout和S-Dropout方法具有随机性,对这两种方法,实验都训练了5个模型,结果取其平均值. 5)实验对比了Dropout与S-Dropout分别应用在全连接层和卷积层的效果,参数P和S在全连接层设为0.5,卷积层为0.2,λ在所有层的取值都为0.7. MNIST由大小为28×28 的手写数字图片组成,数据集中包含60000 张训练图片和10000 张测试图片.LeNet[16]模型在数字分类任务中取得了非常好的效果,本文采用的模型基于LeNet改进,将原来的激活函数sigmoid替换为ReLU,并增加了卷积核的数量,第1个卷积层20个卷积核,第2个卷积层50个卷积核,第3个卷积层500个卷积核,初始学习率0.05,实验共迭代50次.采用不同的正则化方法时,结果如表1所示. 实验对比了Dropout和S-Dropout方法分别在不同层上的效果.训练过程中,L2正则化已经完全拟合了训练数据,预测误差却相对较大,已产生过拟合现象.Dropout和S-Dropout方法有效缓解了过拟合,这与模型组合了多个局部结构的特性相关.S-Dropout因为稀疏性限制的引入,进一步降低了预测误差.当所有层都应用S-Dropout正则化时,结果达到最好,可见S-Dropout正则化无论在全连接层还是卷积层都有不错的效果.由于MNIST数据集本身不是很大,在卷积神经网络强大的特征提取能力下,结果几乎已经接近最优,正则化方法的提升幅度都不是很大,但S-Dropout仍然取得了最好的效果. CIFAR-10包含6万张32×32的RGB图片,共分为10个类别.训练数据50000张图片( 每类5000张),测试数据10000张图片.为了测试S-Dropout正则化方法在不同规模的网络中的表现,设计了两种卷积神经网络模型.网络A基于文献[5]提出的Dropout模型的改进,是一种简化的模型,主要为了达到快速训练的目的.该网络包含3 个卷积层,前两个卷积层由64 个5×5 的卷积核构成,第三个卷积层采用128个3×3的卷积核,池化层选择大小为3的池化区域,以步长2 实施池化操作,第一个池化层为最大池化,后两个池化层为平均池化.倒数第二层是128个节点的全连接层,最后的softmax层输出整个网络的分类预测结果.网络B采用文献[18]介绍的NiN(Network in Network)网络,共有三个模块,每个模块包含一个卷积层和一个由1×1卷积核组成的多层感知器(MultiLayer Perceptron,MLP),卷积层有192个卷积核,后面接一个MLP,迭代次数为100次.MLP能有效的提高模型的表达能力,同时由于大量1×1卷积核的加入,参数数量和训练时间也会增加.实验分别在MLP和所有层上应用Dropout和S-Dropout方法,表2所示为在两种模型下的结果. 由表2可以看出,网络A在第一层应用S-Dropout可以使效果得到进一步提升,而在所有层应用S-Dropout反而使结果下降.这是因为网络A是简化的模型,本身参数不多,而卷积层需要对样本进行特征提取,特征的信息含量尤为重要,又由于参数共享使卷积层本身参数较少,删除过多节点造成信息损失,所以在多个卷积层上删除部分节点会使误差增大.另一方面,只在第一层卷积层上使用具有较小稀疏度值的S-Dropout相当于对样本加入部分输入噪声,类似于降噪自编码器[19]的效果,可以使网络学习到一定的降噪能力,可以更好的防止过拟合现象.而Dropout方法只在网络A中的全连接层有效.可见本文方法在简单的模型上适用的层数更多.网络B由于拥有大量参数,使预测误差大大降低,而且无论是Dropout还是S-Dropout方法,都能应用在网络B的所有层上. CIFAR-100数据集与CIFAR-10类似,不同之处在于它增加了图片类别数到100类,包含50000 张训练数据( 每类500张)及10000 张测试数据.相较于CIFAR-10,CIFAR-100的训练数据相当有限,需要更复杂的模型拟合训练数据,网络A不足以达到可观的精度,所以只使用网络B进行实验,且各层参数保持不变.结果如表3所示,在CIFAR-100有限的训练数据下传统的正则化方法并没有很好的泛化能力,而S-Dropout避免过度拟合训练数据的同时降低了预测误差,整体趋势与CIFAR-10相一致,可见在训练数据不足的情况下,本文方法效果提升明显. 表3 不同正则化方法在CIFAR-100数据集上的结果Table 3 Results of different regularization methods on the CIFAR-100 dataset 正则化方法使具有大量参数的模型在面对小样本训练集时不容易产生过拟合,为了测试本文方法在小样本上的效果,随机的从MNIST数据集中选择大小为100、500、1000、5000、10000和50000的样本来比较L2、Dropout和S-Dropout正则化的效果,使用4.1节中介绍的改进LeNet模型和参数设置,不同的是迭代次数根据样本集的大小会有所改变,样本数量较小时模型收敛速度变慢,相应的迭代次数就需要增加,训练时如果连续10次迭代误差不再减小时就停止.训练完成后,在测试集上的预测误差如图5所示. 图5 样本数量对预测误差的影响Fig.5 Effect of the number of samples on predictive errors 对于样本数量小于1000的极端情况,Dropout和S-Dropout都没有改进预测误差,原因是此时的训练样本太小,模型有足够的参数拟合训练集,甚至是删除部分节点所产生的噪声数据也进行了拟合.而随着训练样本数量的增加,S-Dropout的效果开始提升,总的预测误差也不断减小,图5中所示,在样本数量达到5000时S-Dropout的误差已经低于L2,可见在样本数量达到一个比较小的阈值时,本文方法就体现出较好的效果,且样本越多误差越低. S-Dropout具有两个可调节的参数S和λ,其中参数S称为稀疏度,代表模型中删除的节点所占的比率,取值为0到1之间,值越大删除的节点数越多,稀疏度越高.本节通过调节参数S验证不同的稀疏度带来的效果变化情况.选择4.1节中改进的LeNet模型,分别在全连接层和卷积层上进行验证,使S的取值从0到0.9变化,每间隔0.1训练一个模型,并将Dropout方法中节点被删除的概率P取同样的值进行对比. 如图6所示是S在全连接层上的变化对预测误差的影响.S在0.4到0.7之间取值时,曲线趋于平滑且预测误差达到最低,当S为0时,没有节点被删除,相当于使用原网络进行训练,S过大时被删除的节点过多,模型的表达能力会降低.可见在全连接层上选择适中的稀疏度使模型达到最优,而同样的取值下本文方法比Dropout更优,比较理想的取值为0.5. 图6 全连接层上稀疏度的变化对预测误差的影响Fig.6 Effect of the change of sparsity on the prediction error of the full connection layer 如图7所示是参数S在卷积层上的变化对预测误差的影响,在取值0.2和0.3附近时预测误差达到最小.当卷积层上的S取值过大时,预测误差上升很明显,这是因为卷积层用于特征提取,删除过多的节点造成信息损失,符合4.2节中在CIFAR-10上的实验结果及推论,所以本文在卷积层上的稀疏度选择较小的值0.2,保留了足够的特征量,同时又达到了稀疏化的效果.且参数S在同样的取值下,本文方法的结果优于Dropout. 图7 卷积层上稀疏度的变化对预测误差的影响Fig.7 Effect of the change of sparsity on the prediction error of the convolutional layer S-Dropout中的参数λ称为随机因素,用来确定高激活节点与低激活节点分别被删除的比率.根据激活值大小选择节点使模型具有更强的特征提取能力,同时通过一定的随机性增强模型的鲁棒性,参数λ正是确定这种随机性的因素.为了找到随机因素的最优取值,在S取不同值的情况下,使λ从0.5到1变化,间隔为0.05,利用LeNet模型,在MNIST数据集上进行对比验证. 如图8所示,当λ取值为1的时候,删除的节点全部从低激活值中选择,此时模型保留所有高激活值部分,相当于失去了随机性,节点是否被删除完全依赖于激活值大小,但泛化性能并不理想,可见保留部分低激活值的节点是能够提升最终结果的.当λ取0.5时,随机性达到最大,节点是否被删除完全随机决定,在理想情况下与Dropout具有相等的效果,但也没有得到最低的预测误差.而根据图8中的曲线,在所有S的不同取值下,λ在0.7附近的变化都达到了较理想的结果,这也是本文选择的取值.可见模型的某一层在选择了理想的稀疏度后,通过调节λ到合适的值,可以进一步降低预测误差. 图8 稀疏度取不同值时随机因素对预测误差的影响Fig.8 Effect of random factors on prediction error with different values of sparsity 从以上已经看到,具有稀疏结构的卷积神经网络在防止模型过拟合方面具有更好的效果,从稠密的样本空间中提取的稀疏特征向量具有更好的可区分性.为了验证模型是否提取了稀疏的特征向量,将5000个测试样本通过改进的LeNet模型提取特征向量,特征向量是从模型的全连接层获得的输出值,每个向量500维.图9所示是特征向量输出值的统计直方图,左边是每张测试样本激活的节点数量,右边是被激活的节点对应的图片数量,即有多少张样本可以激活此节点,根据图9的结果可知,使用S-Dropout正则化后,无论是被激活的节点数还是激活节点的图片数都取得了更小的值(直方图往左移动),模型确实提取到了更稀疏的特征向量,在图像分类任务中可以达到更优的泛化性能. 图9 特征向量输出值的统计直方图Fig.9 Statistical histogram of eigenvector output values 本文提出一种稀疏性Dropout正则化方法,并将其应用于卷积神经网络,不仅具有组合多个模型结果的优点,防止过拟合现象的产生,而且对激活值增加稀疏性限制后,能针对不同的样本产生特定的对样本敏感的局部结构,有效提升了模型的泛化能力.删除部分节点减少了模型参数,稀疏性限制保留高激活值节点,增强了模型的特征提取能力,随机因素的加入又一定程度上提高了模型的鲁棒性.然而,通过节点激活值大小进行稀疏性限制略显简单,后续可以通过节点间相关性的大小增加限制,从而得到更理想的效果.
mj~Bernoulli[(1-λ)S],r=rm+
mj~Bernoulli(λS),r=rm-
Fig.4 Calculation process of sparse dropout regularization4 实验结果与分析
4.1 MNIST数据集上的实验结果
4.2 CIFAR-10数据集上的实验结果
4.3 CIFAR-100数据集上的实验结果

4.4 样本数量的影响

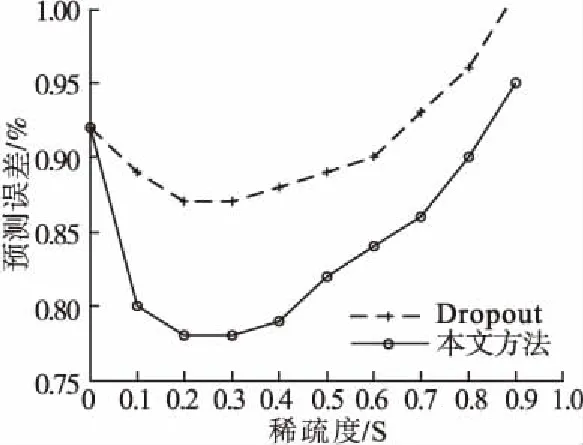
4.5 稀疏度的选择

4.6 随机因素的选择

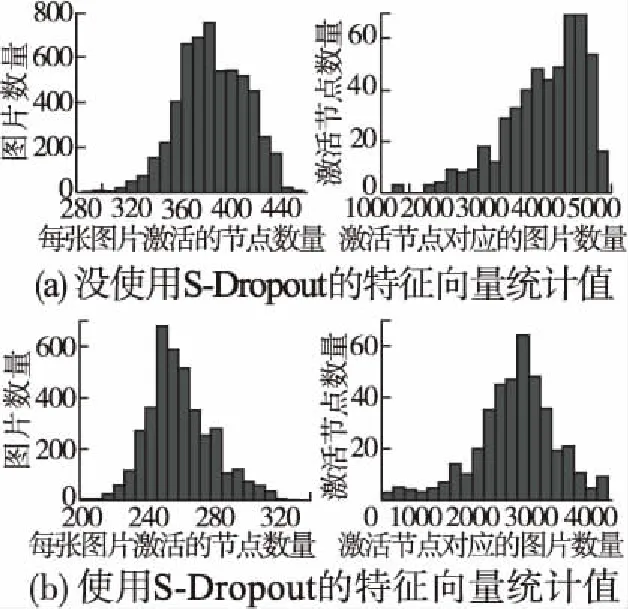
4.7 特征的稀疏性
5 结束语
