数种基于SPSS统计工具的聚类算法效率对比
2018-11-19吕正萍纪汉霖
吕正萍,纪汉霖
(上海理工大学 管理学院,上海 200093)
0 引言
随着大数据技术的发展,数据挖掘技术备受关注,作为其重要组成部分的聚类分析技术已广泛用于数据分析、图像处理、市场研究等多种领域[1-3]。聚类分析根据数据特征将其进行分类,尽可能突显类与类之间的差距,使类的数据差距尽可能相近,即拥有相似特征的数据被聚为一类。聚类分析同时也是一种无监督的学习过程,很难选择最佳聚类分析方法并达到有效聚类个数。
目前对聚类算法的研究及应用集中在两个方面:
(1)聚类算法改进。众多专家和学者对数据聚类方法算法进行了改进和创新,包括K-means聚类、系统聚类、两步聚类,以提高算法精确性与稳定性,改善聚类性能。改进方法主要分为3种:①通过对聚类初始中心的选择,改善聚类有效性。程艳云、周鹏[4]提出动态分配聚类中心的改进K均值聚类算法,该算法改进了K均值初始聚类中心的选取方法,直接有效地选择出最佳初始聚类中心并进行K均值聚类计算;周鹿扬等[5]提出一种基于聚类中心的快速聚类算法,该方法选择一组高密度分布的聚类中心,将聚类中心周围的对象划分到离其最近的聚类中心形成子簇,再根据子簇之间的连通性完成子簇合并;②对聚类过程中最佳聚类个数的研究。刘飞等[6]采用SSE对簇个数进行度量,提出一种能够自动确定聚类个数的聚类方法。费贤举等[7]通过改写软子空间聚类算法的目标函数,并结合数据簇大小对各个数据簇的影响,使聚类结果与初始聚类个数和初始聚类中心无关,达到有效的聚类分析结果;③通过对聚类算法的改进与优化,改善聚类有效性。朱林等[8]提出基于数据流的软子空间聚类算法,利用模糊的可扩展聚类算法策略,将软子空间聚类方法应用于流数据聚类分析,以有效应用于高维数据流或者大规模数据的聚类研究中心。杨扬等[9]提出基于属性值变化程度定权的聚类算法,该算法考虑了聚类对象各属性值对聚类划分的影响程度,并通过ratio值对其进行量化,从而提高聚类运算精确度。
(2)聚类分析方法的应用。统计分析软件SPSS中三大聚类方法(K-means聚类、系统聚类、两步聚类)被广泛应用于交通管制、图像处理、环境监测、商业市场分析等领域,根据聚类结果给出相关建设性建议或提出有效算法[10]。例如,杨越等[11]在简化航路网中,采用欧氏距离相似性度量,对不同航路点的时间序列进行系统聚类,划设应急航路,减累地面空管单位的管制压力。夏晨木等[12]通过运用K-means聚类方法,将裂缝表面的三角网格进行分类,实现与普通孔隙表面三角网格分离和区分的结果,以此提出一种新的岩石三维图像裂缝提取算法。孙亚男等[13]应用聚类分析方法研究长三角地区大气污染的城市联动及动态交互影响,以提升大气污染联防联控成效。还有研究将聚类方法应用于投资者P2P网贷平台的选择[14]、商品精确营销[15]、图像分割处理[16]等。以上研究关注于聚类方法的应用及聚类与其它方法的结合,并没有对不同聚类方法的有效性进行比较。
本文以SPSS为聚类工具,使用EXCEL中VBA计算分析数据点之间的距离,对比分析各种聚类算法之间的优劣,并给出相应结论。
1 聚类原理
聚类分析是一种建立分类的多元统计分析方法,能将一批样本(或变量)数据根据其诸多特征,在没有先验知识的情况下,按照性质的亲疏程度进行自动分类,产生多个分类结果,其结果是同一个类之内的个体特征具有相似性,不同类的个体特征差异性较大。
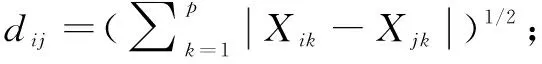
一般采用不同距离公式会得到不同分类结果,本文采用欧式距离进行分类。
2 SPSS聚类模型概述
SPSS是一款成熟的统计软件,其聚类模型在业内具有典型的代表意义,SPSS目前采用K-means、系统聚类、两步聚类3种聚类方法。
2.1 K-means聚类
K-means聚类方法也称快速聚类,是一种应用广泛的经典聚类算法,将数据看成K维空间上的点,以欧式距离作为测度个体“亲疏程度”的指标,模型收敛速度快,算法简单,并能有效处理大数据集,不过该方法只能处理连续的样本数据。形式最简单的算法包括以下3个步骤:
(1)将所有变量分成K个初始聚类。
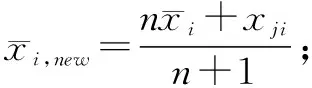
(3)重复步骤(2),直到所有类的核心不再改变为止。
K-means聚类只能产生指定类数的聚类结果,在应用K-means聚类分析方法时,对于变量之间存在较大差异时,通常先采用标准化处理,再进行下一步聚类分析。因此,K-means聚类又分为K-means未标准化聚类和K-means标准化聚类。
2.2 系统聚类
系统聚类(Hierarchical Clustering)分析法又称层次聚类分析法,是根据观察值或变量之间的亲疏程度,将最相似的对象结合在一起,以逐次聚类的方式将观察值分类,直到最后所有样本都聚成一类。该方法既可以处理连续变量,也可用于名义变量的处理。
系统聚类过程[17]为:
(1)假设总共有n个变量,将每个变量独自聚为一类,共有n类。
(2)根据变量距离公式,把距离较近的两个变量聚合为一类,其它变量仍各自聚为一类,共聚成n~1类。
(3)将“距离”最近的两个类进一步聚成一类,共聚成n~2类。
以上步骤持续进行,直到聚合的数目达到预定为止。进行系统聚类之前,需要定义类间距离,根据类间距离定义的不同,形成不同的聚类方法,常用的类间距离定义有类平均法、可变类平均法、可变法、最短距离法、最长距离法、中间距离法和离差平方和法。本文运用离差平方和法,该方法又称Ward法,其原理是同类变量的离差平方和应当较小,类与类的离差平方和较大,按常规将数值标准化到Z分数,以增强常用方法的可比较性。
2.3 两步聚类
两步聚类法(Two Step Clustering, TSC)又称两阶聚类法,当数据样本中有名义变量时,可选择该聚类方法,与SPSS中K-means和系统聚类法不同的是该方法采用数的极大似然估计值度量变量之间的距离,并能根据施瓦兹贝叶斯准则(BIC)或Akaike信息准则(AIC)等指标自动确定最佳聚类个数[18]。
该方法分为两阶段:①预聚类阶段:采用BIRCH算法中CF树生长的思想,逐个读取数据集中数据点,在生成CF树的同时,预先聚类密集区数据点,形成诸多小的类:②聚类阶段:逐个合成子类,直至达到期望的类数量。
3 实验
3.1 有效性指标
聚类有效性评价指标分为外部评价指标和内部评价指标两大类,常用的外部评价指标包括F_measure指数、Rand指数和Jaccard系数,常用的内部评价指标包括Cophenetic相关系数和Huberts 统计指标[19]。Davies等[20]提出聚类有效性指标DB(-),该有效性指标以类内样本点到其聚类中心的距离估计类内紧致性,用聚类中心之间的距离表示类间分离性。本文参考该指标,以类内样本各个点到其聚类各中心的距离平均值作为比较类内的紧致性指标(指标1),以聚类各个中心之间的距离平均值作为比较类间的分离性指标(指标2)。计算公式为:
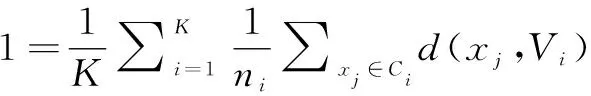
(1)
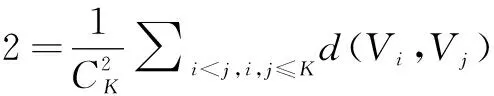
(2)
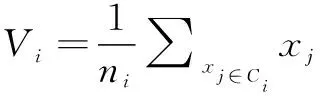
3.2 实验描述
为比较统计分析软件SPSS中3种聚类方法对数据的处理效率和效果,本文随机选取了99组数据,将数据分为3组,其中32组数据用于K-means聚类、系统聚类之间的比较,29组数据用于K-means标准化聚类与系统聚类的比较,38组数据用于两步聚类与系统聚类的比较,并使用SPSS软件和VBA编程语言对比分析K-means聚类、K-means标准化聚类、两步聚类、系统聚类的算法效率。
分析和计算步骤如下:
步骤1:用SPSS软件把样本聚类处理为3个类、4个类、5个类,每一行数据都有其分类号,将分类后的结果(.sav文件)存为excel文件;
步骤2:在保存数据的excel文件中,用VBA(Excel内嵌的编程语言)计算各个类中心点之间的距离平均值(类之间离得足够远——见3.1节中的指标2 )、各个类的点到中心点距离的平均值(类里的距离足够小——见3.1节中的指标1)。
步骤3:根据指标1和指标2,对比分析在不同数据特征下,何种SPSS聚类算法效率更高。
3.3 实验结果
通过对比分析观察聚类算法效率,得到对比结果。
3.3.1 K均值未标准化聚类与系统聚类方法比较
由表1可以看出,通过对32组数据进行K-means未标准化聚类和系统聚类方法处理,分别得到为3个类的聚类、4个类的聚类、5个类的聚类,分类增强实验结果的可比性,3种分类中K均值未标准化的指标1明显小于系统聚类的指标1,而且K均值未标准化指标2明显大于系统聚类的指标2,因此K-means未标准化聚类方法明显优于系统聚类。此外系统聚类方法的指标1随着聚类个数增加,由467 426.131 9逐步降到417 052.567 1,指标2由381 995.229 4逐步增加到489 344.832 1,因此得出,系统聚类有效性随着系统聚类个数的增加越来越好。
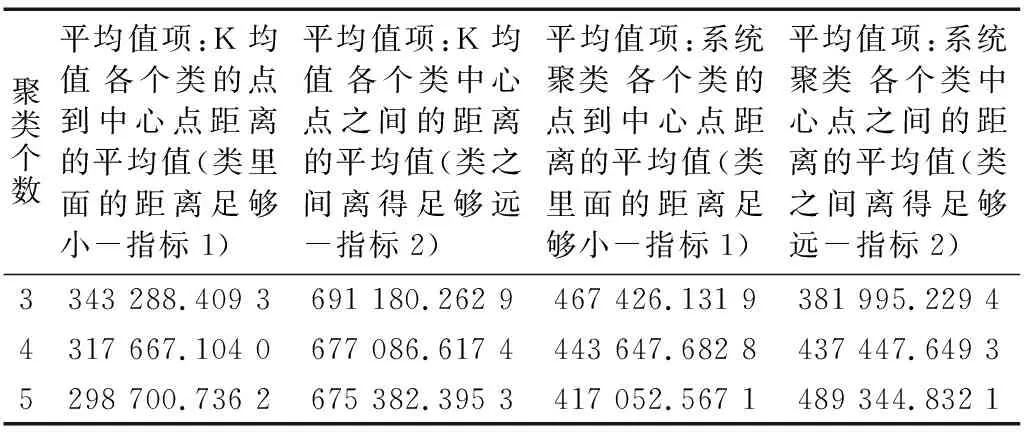
表1 32组K均值未标准化与系统聚类比较
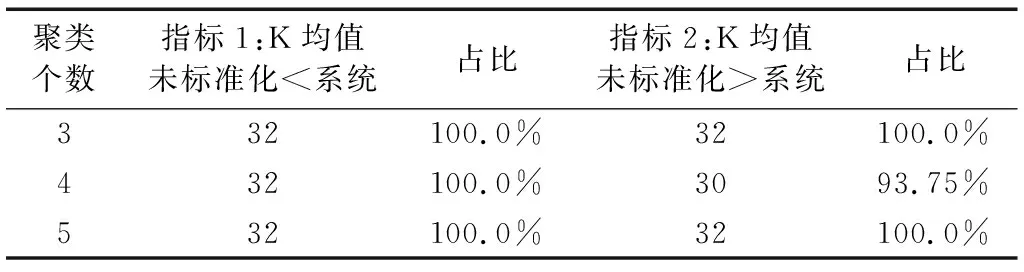
表2 32组K均值未标准化与系统聚类对比
此外,由表2占比统计可以看出,K均值未标准化绝对优于系统聚类方法,不论数据本身大小如何,在K均值未标准化聚类方法与系统聚类之间选择时,首选K均值未标准化聚类方法。
根据32组数据的统计特征进行划分,如表3所示将数据分为数据1和数据2,数据1的样本数据规模小于数据2。本文类似表格还有表6、表9。

表3 32组K均值未标准化与系统聚类数据统计特征
由表3可以看出,在考虑数据规模时,只有数据取值范围很小且数据变动也很小时,可以任意选择K均值未标准化或系统聚类方法,即两者在数据处理上无差别;而在数据规模较大时,则应选择K均值未标准化聚类方法。因此也验证了表2的结论:不论数据规模如何,都应选择K均值未标准化聚类方法。
3.3.2 K均值标准化聚类与系统聚类方法比较
由表4可以看出,通过对29组数据进行K-means标准化聚类和系统聚类处理,分别得到3个类的聚类、4个类的聚类、5个类的聚类,通过分类增强实验结果可比性,3种分类中K-means标准化聚类方法指标1要比系统聚类指标1小,且K-means标准化聚类方法指标2也要比系统聚类指标2大。从表中可以看出,系统聚类方法的指标1随着聚类个数增加,由289 158.442 8逐步降到267 296.610 8,指标2由278 197.103 3逐步增加到302 074.593 5,因此系统聚类有效性随系统聚类个数的增加越来越好,但K-means标准化聚类方法一直优于系统聚类。
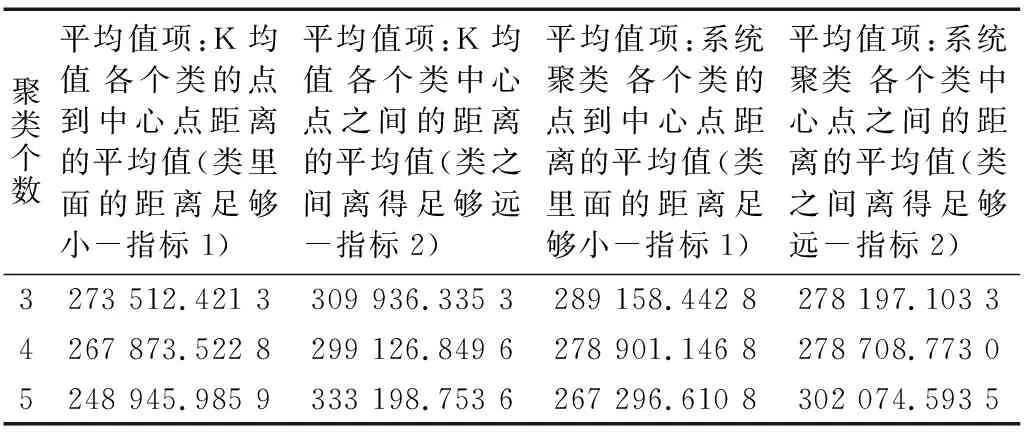
表4 29组K均值标准化聚类与系统聚类比较
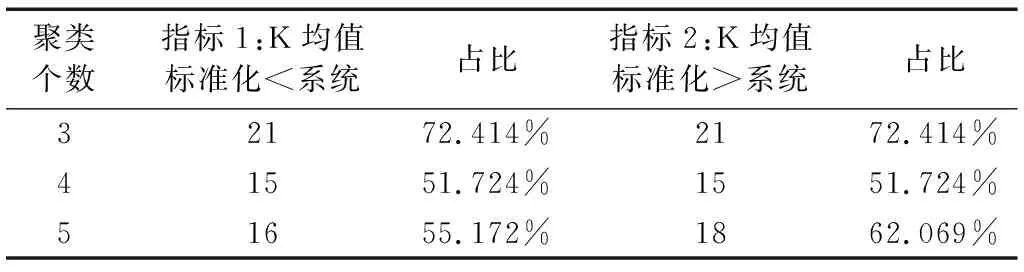
表5 29组K均值标准化与系统聚类对比
由表4还可以看出,K均值标准化聚类方法比系统聚类方法有效,且随着聚类个数的增加,系统聚类与K均值标准化聚类方法的差距将缩小。从两类指标的占比可以看出,K均值标准化聚类的有效性高于系统聚类方法,但随着聚类个数的增加,差距有缩小的趋势,指标1由原来的72.414%降到51.724%和55.172%,指标2由原来的72.414%降到51.724%和62.069%。由此可以得出,K均值标准化聚类的有效性会一直优于系统聚类方法。
根据以上结果,本实验对这29组数据进行数据特征比较,结果如表6所示。
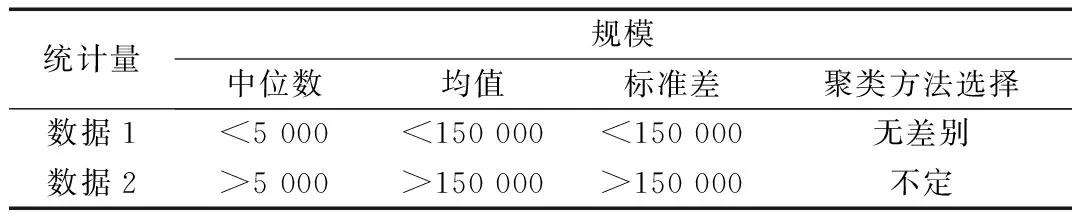
表6 29组K均值标准化聚类与系统聚类的数据统计特征
因此,在选择均值标准化和系统聚类时,如果数据规模比较小,可以选择任意一种方式;而在数据规模比较大时,则应选择K均值标准化聚类方法。
3.3.3 两步聚类与系统聚类方法比较
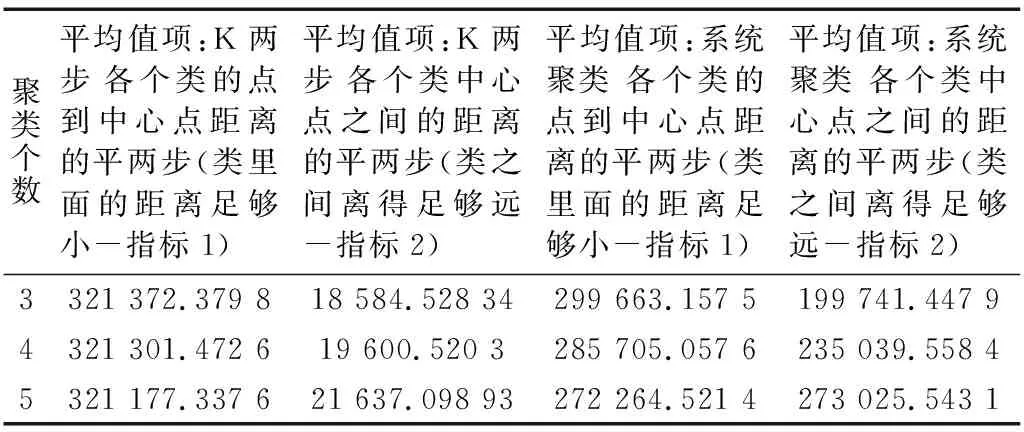
表7 38组两步聚类与系统聚类比较
由表3可以看出,通过对38组数据进行两步聚类和系统聚类处理,分别得到为3个类的聚类、4个类的聚类、5个类的聚类,通过如此分类增强实验结果可比性,而这三种分类的系统聚类方法指标1都小于两步聚类的指标1,系统聚类方法的指标2大于两步聚类的指标2,由此可以得出,系统聚类方法明显比两步聚类有效。
同时,由表8可以看出,系统聚类方法的总体有效性要优于两步聚类方法,并且随着聚类个数的增加,指标1由3个类的78.95%增加到5个类的92.11%,指标2由3个类的84.21%增加到5个类的94.74%。由此可见,系统聚类的有效性随着聚类个数的增加将越来越优于两步聚类方法。
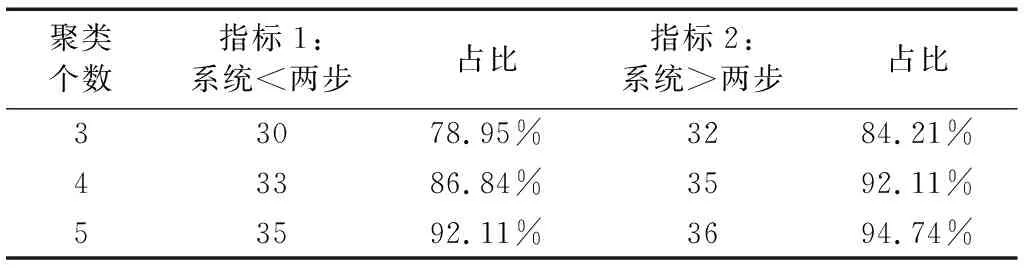
表8 38组两步聚类与系统聚类对比
根据以上结果,本实验对这38组数据进行数据特征比较,结果如表9所示。
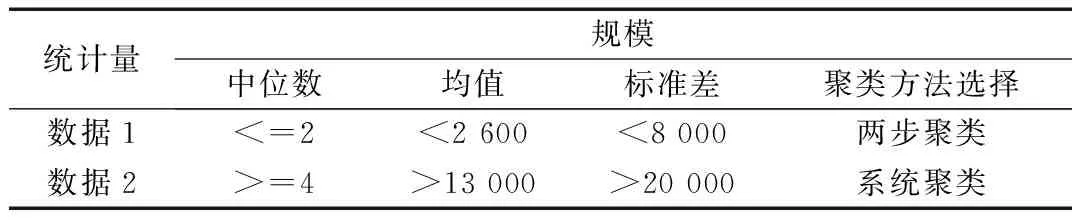
表9 38组两步聚类与系统聚类数据统计特征
由表9可知,在选择两步聚类和系统聚类时,如果数据规模比较小,则可以选择两步聚类;而在数据规模比较大时,则应该选择系统聚类方法。
3.4 实验分析及建议
本文通过对数据进行两两聚类分析比较,分为3个类、4个类、5个类,一方面说明数据可比性,另一方面也验证数据可靠性。此外,本文通过两项指标(类间距、类内距)综合说明实验结果的优良性。
综上分析可知:①在判断数据类型、确认使用的聚类分析方法后,发现K-means聚类(K均值未标准化、K均值标准化)效果明显优于系统聚类效果,系统聚类也明显优于两步聚类;②只有系统聚类分析方法随着聚类个数的增加而越来越有效,K-means聚类和两步聚类无该趋势。
由此,本文给出以下建议:①在进行聚类分析时,根据变量的连续特征,在K-means聚类与系统聚类之间选择时,首选K-means聚类方法。根据数据规模大小,规模较小时则可以任意选择,而规模较大时选择K-means聚类方法;②当数据中含有不连续变量、在两部聚类和系统聚类之间选择时,若数据规模较小,可选择两步聚类;若数据规模较大,则应选择系统聚类方法;③进行系统聚类分析时,尽可能选择较多的聚类个数,能有效提高聚类精确度。
4 结语
本文通过对99组数据进行聚类分析比较,最后得出优先选择何种聚类方法的条件和规则,为如何选择更合适的SPSS方法给出了有价值的参考。在判断聚类分析方法效率时选用两个指标,很好地说明了变量之间的亲疏,对其它数据挖掘工具的使用也有一定启发。限于SPSS软件本身的缺点,如导入数据规模有限,不能对数据规模进行详细划分,亦不能处理海量数据,因此,如何对海量数据进行聚类分析,并达到有效的聚类效果将是下一步研究方向。
