级联光束分离器的纠缠特性及其应用∗

贾芳 张魁正 胡银泉 张浩亮 胡利云3)† 范洪义

1)(江西师范大学,江西省光电子与通信重点实验室,南昌 330022)2)(中国科技大学材料科学与工程系,合肥 230026)3)(江西师范大学,量子科学与技术中心,南昌 330022)(2018年2月28日收到;2018年4月11日收到修改稿)

1 引 言

量子纠缠是量子物理中的一个奇异现象.为了验证量子态的非经典特性(包括量子纠缠),实现不同的量子任务,人们需要制备不同的量子态并期望对其实现操控.作为一种线性光学器件,光束分离器是常用于量子态的制备及量子理论等领域的思想实验和现实实验的手段,也是大多数干涉仪的关键部分.此外,光束分离器也是量子力学中纠缠态表象制备的有效方法.例如,利用对称光束分离器可以制备质心坐标Q1+Q2及相对动量P1−P2的共同本征态|η⟩,它构成了一个完备的量子力学表象[1];该表象可用于构建复分数傅里叶变换[2]、纠缠分数傅里叶变换[3,4],通过经典尺度变换⟩可构建双模压缩算符[5]也可以用于描述系统与环境之间的纠缠.基于该表象可以方便有效地求解密度算符主方程,得到密度算符的Kraus算符和表示,并可将特征函数归结为态矢量与热纠缠态表象的内积,从而为分布函数(Wigner函数、特征函数)的时间演化提供了简便的计算方法[6].此外,该表象在求解两体动力学问题、量子隐形传态、量子密集编码、算符恒等式推导等方面有着广泛应用[5,7−11].当两个单模压缩真空态输入光束分离器,可获得双模压缩真空态.该态在量子密钥分发等方面有广泛应用[12,13].

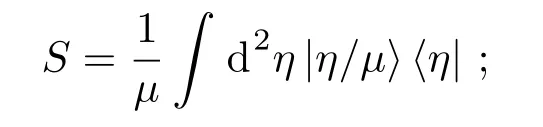
另一方面,光束分离器也被广泛应用于量子信息与量子计算中.为了研究的方便,人们常常用光束分离器来模拟量子耗散,如光束分离器一输入端为真空用于模拟振幅衰减通道,输入热态模拟有限温度通道,压缩热态输入模拟相位敏感的耗散通道[14].这些模拟与相应密度算符主方程的等价性已被证明.当光束分离器一端输入真空,在一输出端进行条件光子数探测,该过程可以用于实现光子扣除,从而制备若干非经典态、改善量子纠缠与量子隐形传输保真度等[15−18].此外,多个光束分离器的组合系统也具有广泛应用.马赫-曾德尔干涉仪由两个光束分离器构成,被广泛用于量子精密测量[19−21];两个共享一端(前光束分离器一个输出作为后一光束分离器的一个输入)的光束分离器组合被用于实现有限维的量子态工程,如可实现连续量子态的截断、离散比特量子叠加态的隐形传输、量子纠缠度改善与压缩度增强等[22−24];两个级联的马赫-曾德尔干涉也被用于制备真空态与单光子态的超叠加,该方案比其他相关方案具有更高的测量概率且具有更高抵抗环境的能力[23];三个不对称光束分离器组成的三个输入与三个输出的系统可用于实现受控非门[25,26].由n个光束分离器组合系统,如算符形式为

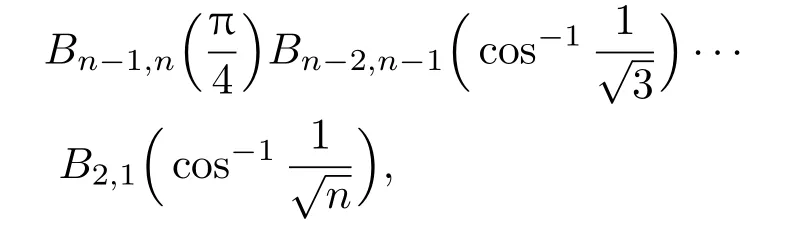
被用于获得多模Einstein-Podolsky-Rosen纠缠态、相干纠缠态表象等[27,28].最近,利用光束分离器算符在表象中的表示,研究表明该算符可分解成多个单模压缩算符、双模压缩算符的乘积[29].

在以上的研究中,一方面,利用Heisenberg绘景中光束分离器算符的变换关系获得量子力学纠缠态表象及其Schmidt分解、光束分离器算符的正规乘积表示等不够直接有效;另一方面,当多个光束分离器组成复杂系统时,计算输出量子态时(在Schrödinger绘景中)通常要逐步将光束分离器算符作用于量子态上,计算过程较为复杂.基于此,注意到在Heisenberg绘景中可直接给出总体算符的变换矩阵以及借鉴压缩算符在坐标表象中自然表示的思想,本文结合有序算符内的积分技术直接导出多个光束分离器级联总算符的正规乘积、紧指数表示、坐标态表象中的表示.同时,基于多级联器件制备新纠缠态表象,直接导出它们的Schmidt分解.该研究方法可推广至线性器件甚至非线性器件组成的任意系统中.

本文第二部分通过简要回顾单个光束分离器的变换关系,建立了Heisenberg绘景中湮没算符的变换矩阵与Schrödinger绘景中产生算符的变换矩阵的对应关系——二者可以通过简单的转置操作联系.这为绘景间的转换提供了直接途径.同时,结合有序算符内积分技术和量子力学表象理论,推导了单个光束分离器算符的正规乘积和紧指数表示.第三部分基于以上方法,进一步考虑了两级联光束分离器总算符的表象表示及其正规乘积,并推广至多个级联光束分离器算符情况.第四部分以两级联光束分离器为例,考察了它们在量子力学表象构建、基于条件测量产生非经典量子态方面的应用.其中,总算符的表象表示与正规乘积形式为计算提供了很大便利.最后是结论部分.

2 单个光束分离器的变换关系及变换算符

2.1 单个光束分离器的变换关系

首先,回顾一下单个光束分离器特点.如图1所示,单个光束分离器由两个输入端、两个输出端构成.用算符a1和a2表示输入场模,b1和b2表示输出场模.由于该过程是一个线性过程,故而输入输出关系可表示为

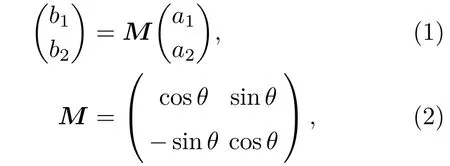
其中矩阵M为单个光束分离器对应的散射矩阵——幺正变换矩阵.为方便,(2)式中忽略了相位因子项.对于无损失光束分离器,输入输出端的总光子数必守恒,即要求

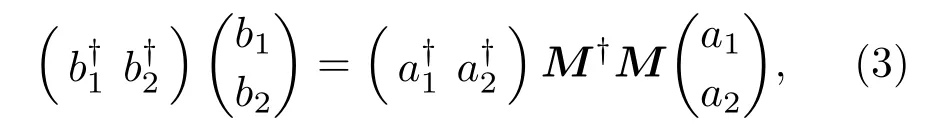
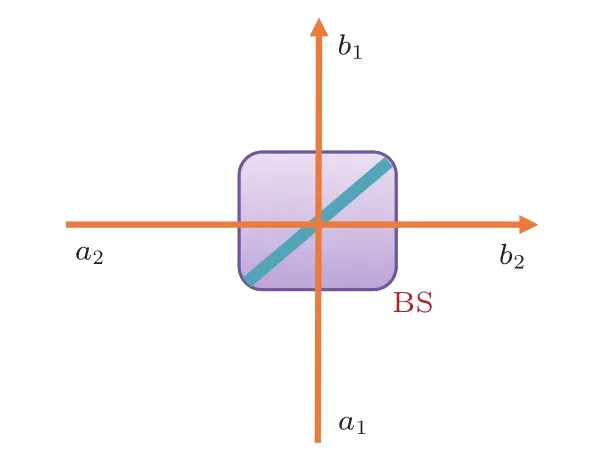
图1 单个光束分离器的输入输出示意图Fig.1.Simple diagram for input-output relation of single beam splitter(BS).

由于算符平均值不依赖于具体的绘景,即在Heisenberg绘景中平均值与(4)式相等,则要求Heisenberg绘景中算符OH演化满足

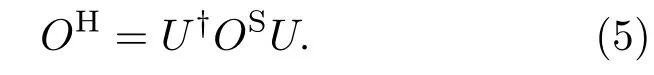
故由(1)和(5)式可知,与光束分离器算符U所对应的输入输出关系为

Mij是(2)式的矩阵元.至此,我们并不知道算符U.为了得到算符U的具体形式或者输出态的具体形式,就需要将问题的讨论转到Schrödinger绘景中去. 不失一般性,设输入态为|00⟩为双模真空态,则输出态为

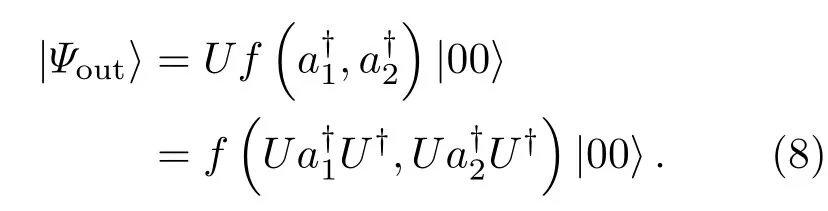
(8)式最后一步中利用了光束分离器算符的线性特征U|00⟩=|00⟩,以及U†U=I. 比较(6)和(8)式易见,在Heisenberg绘景和Schrödinger绘景中需要计算的分别是变换那么,这两个变换之间是如何通过变换矩阵M相联系的呢?注意到,变换UOU†实际上是一个逆变换过程,即将原输出算符看成输入算符,原输入算符看成输出算符——交换了输入输出关系.或者说,以上这个变换实现了算符的变换.故而逆变换的输入输出关系可写为

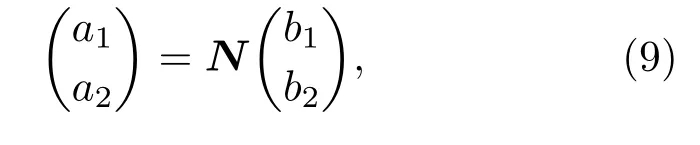
其中散射矩阵N为变换UOU†所对应.联立(1)和

(9)式可得

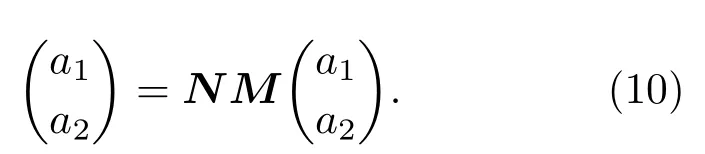
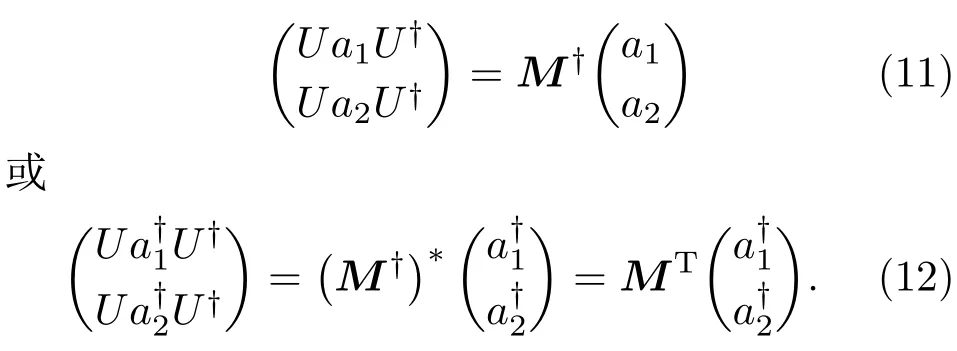
2.2 幺正变换算符U的表象表示及其正规乘积

那么,与变换关系式(1)对应的幺正变换算符U是什么呢? 下面,利用量子力学表象理论方法以及有序算符内积分技术来推导U的具体形式. 设光束分离器两输入端为坐标算符和的本征态⟩和⟩,且⟩和则输出量子态为

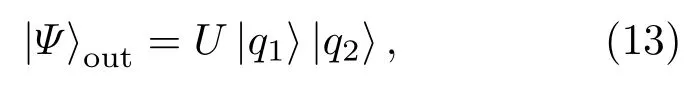
其中坐标态为

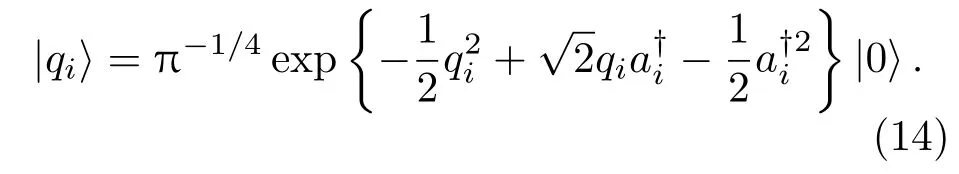
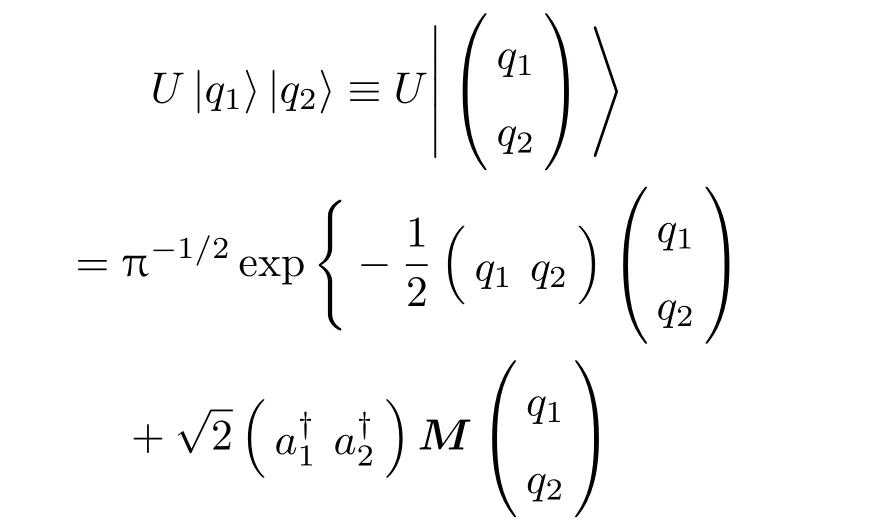
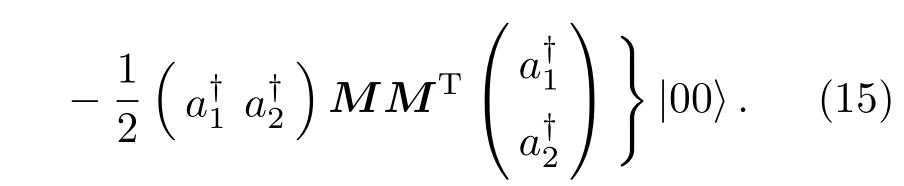
注意到,对于(2)式给出的散射矩阵为实矩阵,则有MMT=MTM=I以及|M|=1,故(15)式可改为

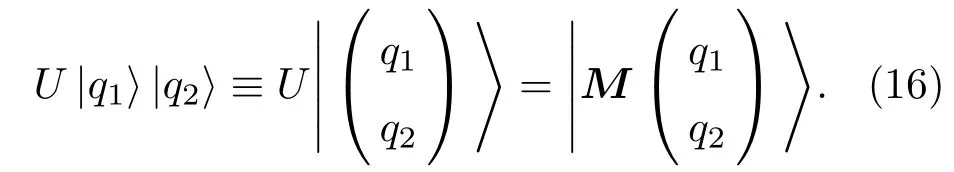
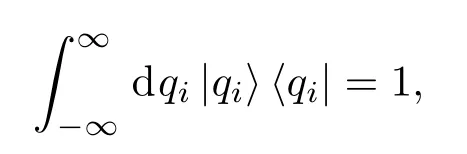
则幺正算符U在坐标表象中可表示为

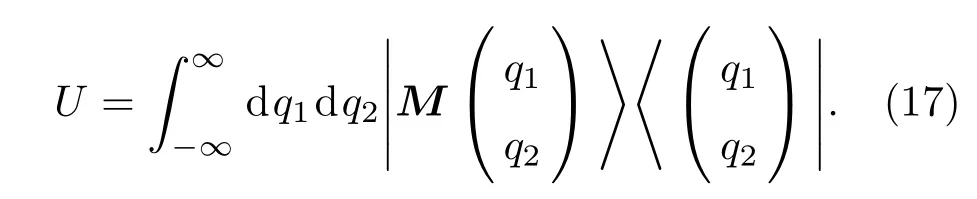
进一步利用有序算符内积分技术可得U的正规乘积形式为[29]

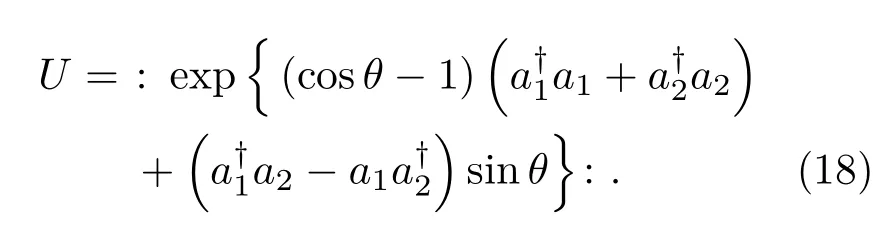
此即光束分离器算符的正规乘积表示.通过(18)式U对θ微商不难获得

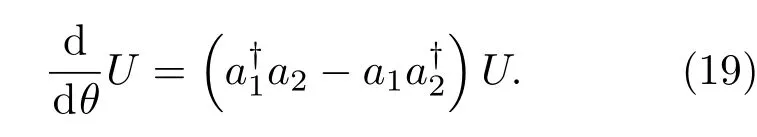
故U的紧指数表示为

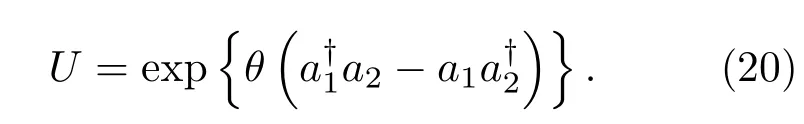
3 级联光束分离器算符的表象表示及正规乘积

3.1 两级联光束分离器算符的表象表示

首先,考虑两个级联光束分离器算符的整体变换关系及其坐标表象中的表示,并由此推导级联光束分离器算符的正规乘积.两级联光束分离器如图2所示.两个光束分离器的变换关系分别为

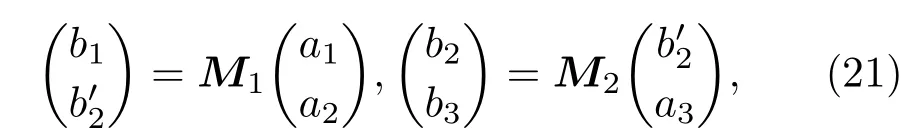
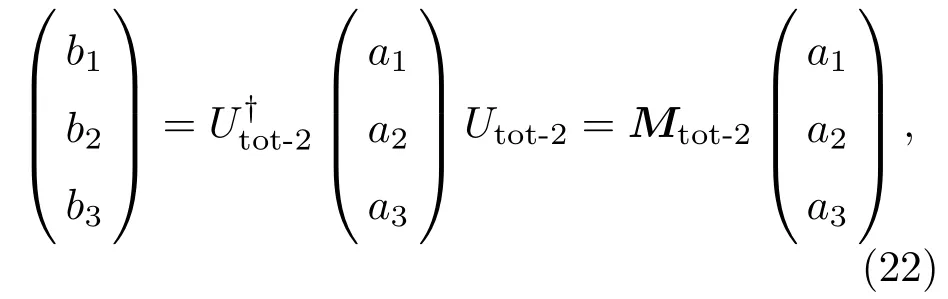
其中总散射矩阵Mtot-2为

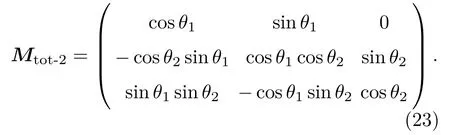
按照推导(17)式的方法直接可得两级联光束分离器算符在坐标表象中的表示为

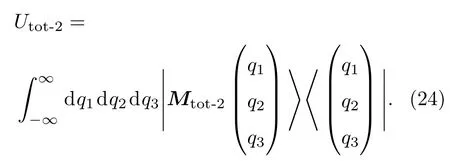
实际上,按照单个光束分离器算符的坐标表示式(17)亦可得Utot-2的坐标表象中的表示式(24).

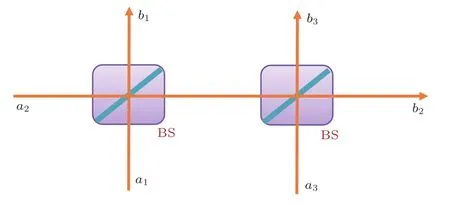
图2 两个级联光束分离器示意图Fig.2.Simple diagram for two-cascaded beam splitters.

3.2 两级联光束分离器算符的正规乘积与紧指数表示

利用有序算符内积分技术和坐标态(14)式、积分式(24)并注意到可得两级联光束分离器算符的正规乘积为

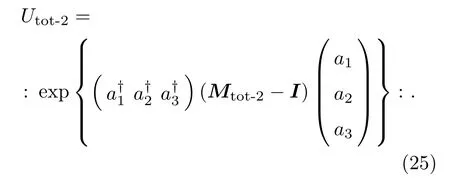
(24)和(25)式在纠缠态表象的制备及在给定输入量子态时计算输出态时有方便有效的应用.利用算符恒等式:可得

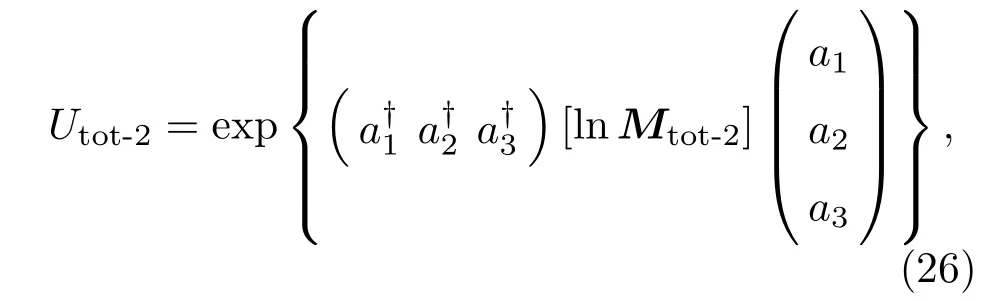
此即级联光束分离器算符的紧指数表示.通过对变换矩阵Mtot-2进行对角化,可进一步获得(26)式不包含对数的具体形式.

3.3 多光束分离器级联

以上讨论可方便地推广至多光束分离器级联的情况.考虑如图3所示的n个光束分离器的级联.对于此类级联,可知n个光束分离器对应的变换矩阵为

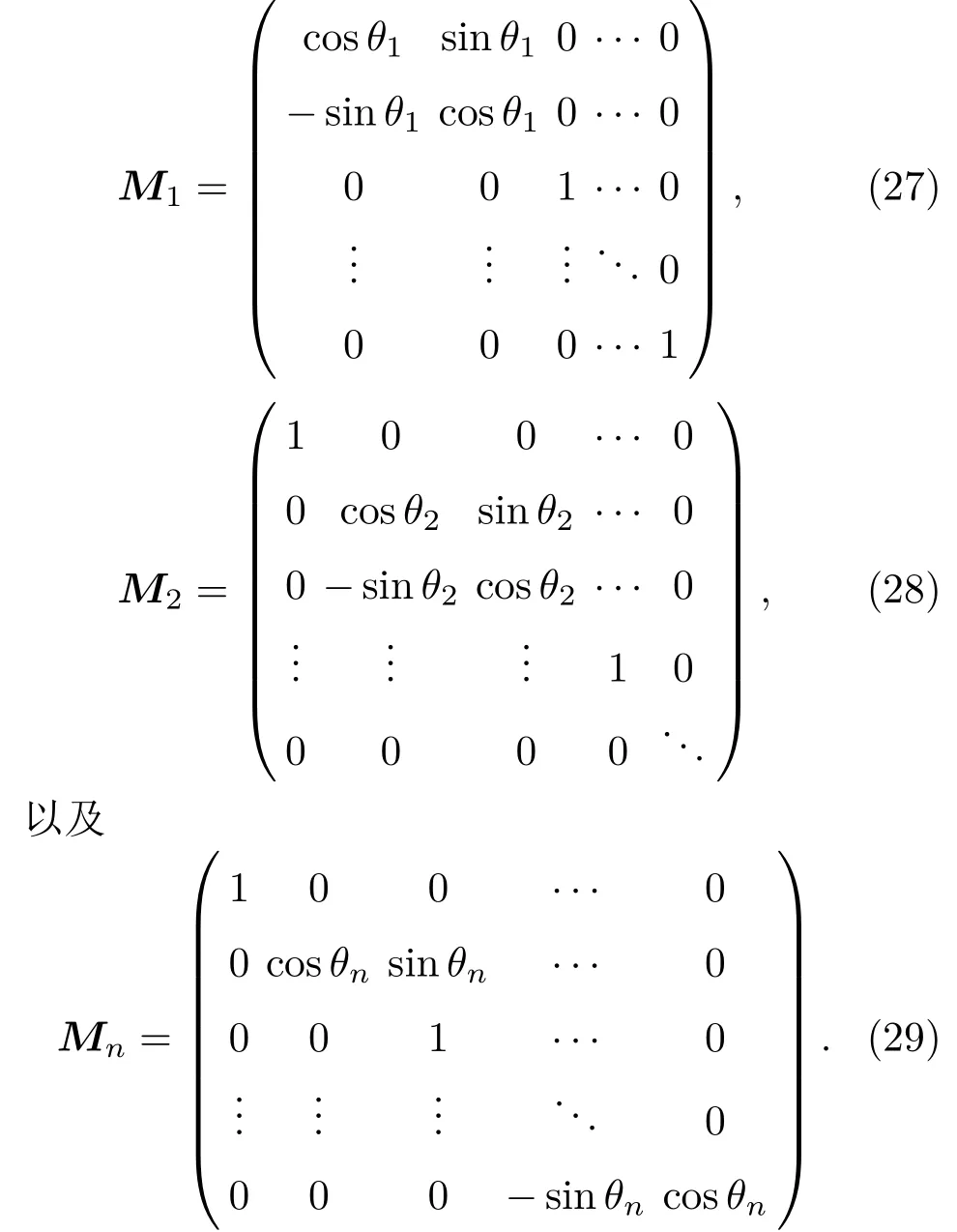
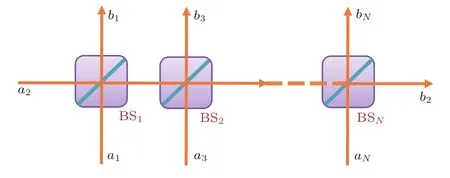
图3 多个级联光束分离器示意图(这里只列出了一种常见形式)Fig.3.Simple diagram for multi-cascaded beam splitters.Here we show an example.

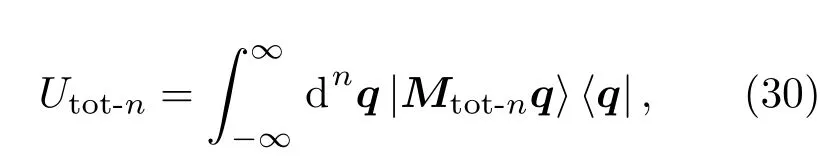
其中

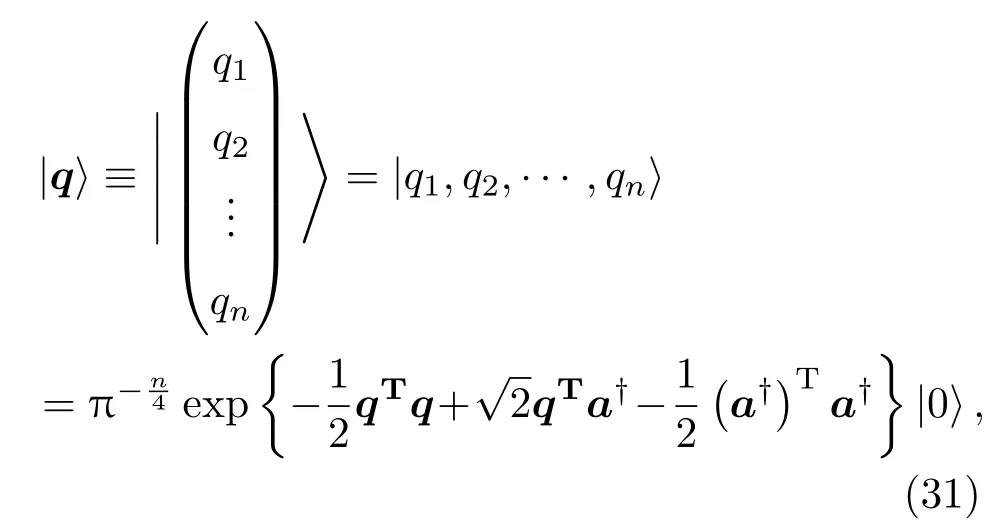
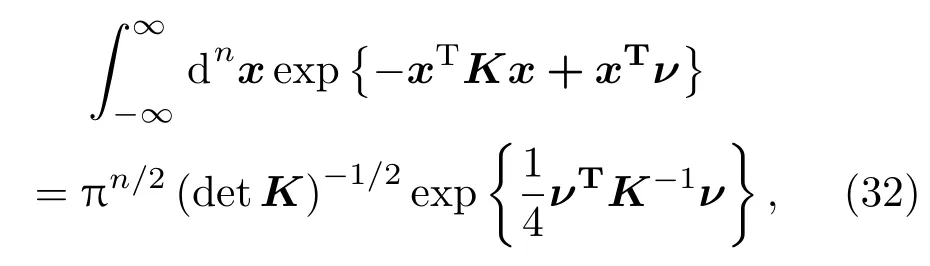
其中K是实对称且正定的n×n方阵,可得Utot-n的正规乘积为

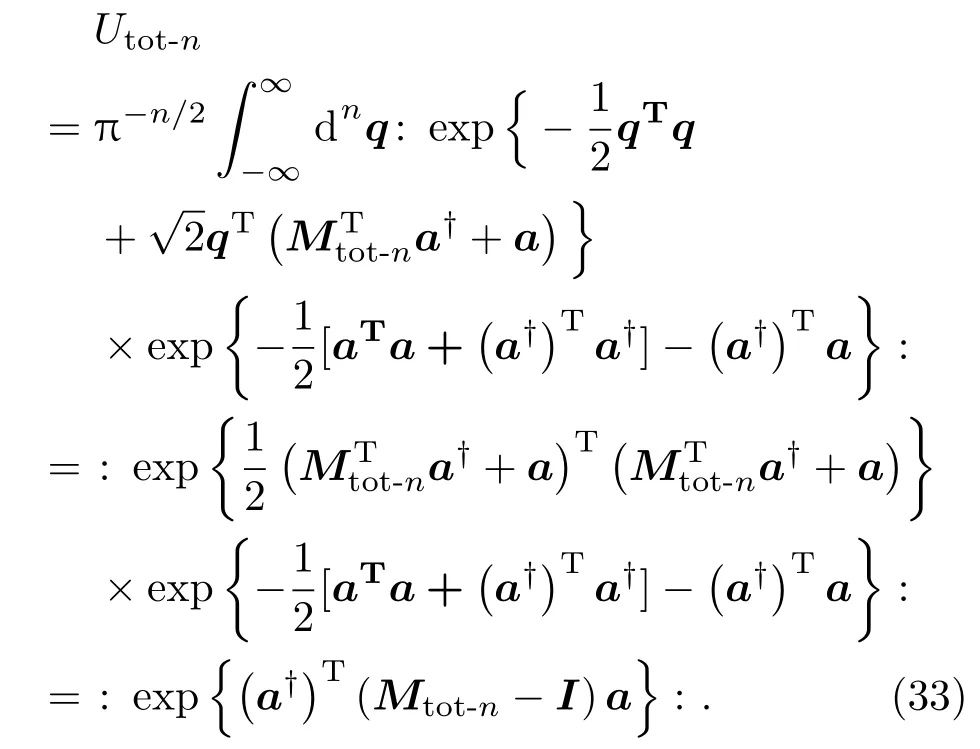
相应的级联光束分离器总算符的紧指数表示则为

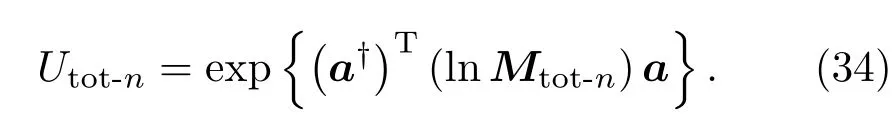
4 级联光束分离器算符的应用

下面,考虑两级联光束分离器算符的表象表示及正规乘积在量子力学纠缠态表象的构造、输出量子态计算方面的应用.实际上,光束分离器的各种组合在量子态的制备中十分易见.以下的讨论方法可直接推广至多光束分离器级联的情况,这里仅以两级联光束分离器为例.

4.1 量子力学表象的制备

首先,利用级联光束分离器算符的表象表示来构造纠缠表象.注意到若3个输入端均为坐标态时,并不能得到纠缠表象,而是3个坐标态的直积态.此外,由(17)式可知,当 a1,a2模分别输入坐标态时输出量子态仍然为坐标直积态,而非纠缠态.因此,考虑 a1,a2,a3模分别输入坐标态动量态和坐标态即输入态为利用(24)式与坐标态、动量态内积关系可得输出态为

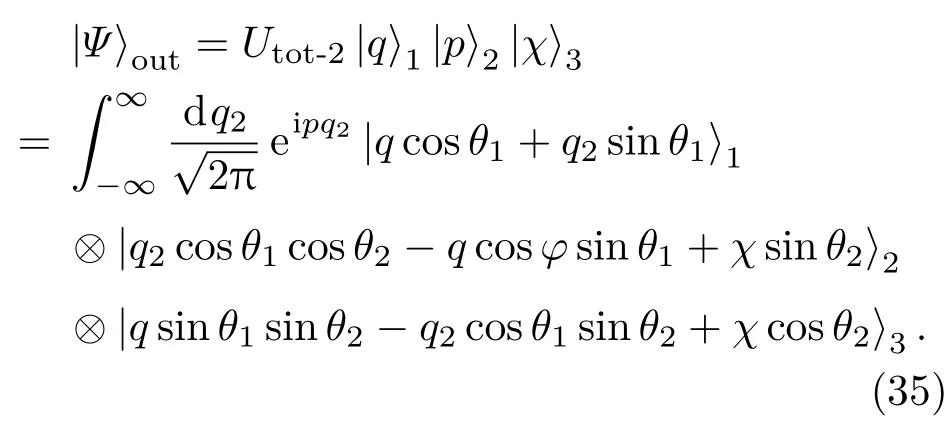
(35)式即为输出态|Ψ⟩out在坐标表象中的Schmidt分解.可见,当两个坐标态和一个动量态输入时,可得到一类新的纠缠态表象,(35)式即是该纠缠态在坐标表象中的表示.那么,该态具体形式是什么?是什么算符的共同本征态呢?利用坐标态的表达式(14),直接积分(35)式可得

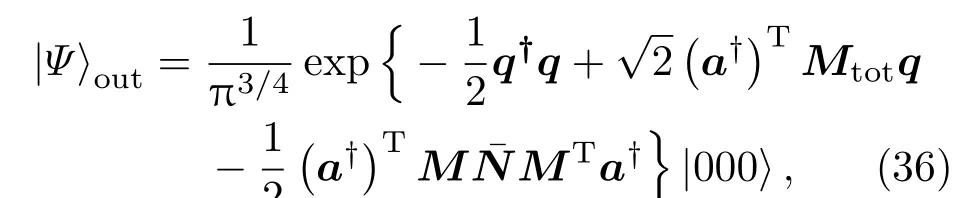
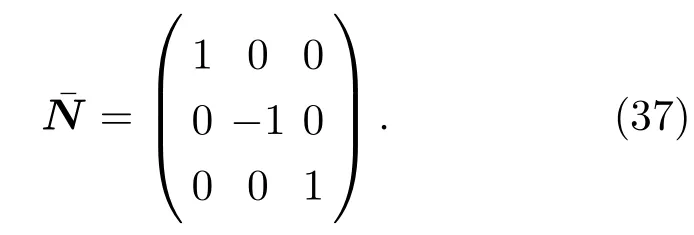
此外,由(22)式可知

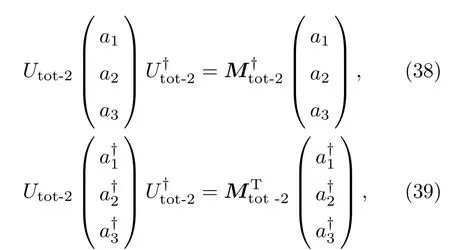
式可得

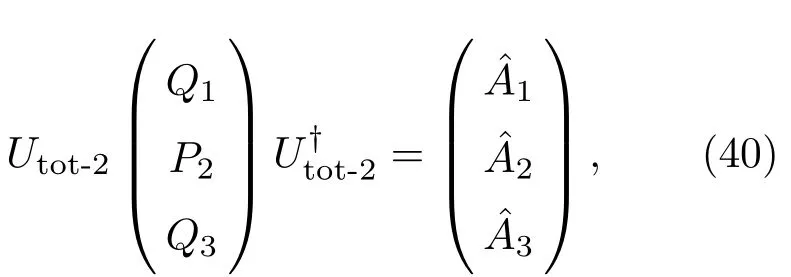
其中

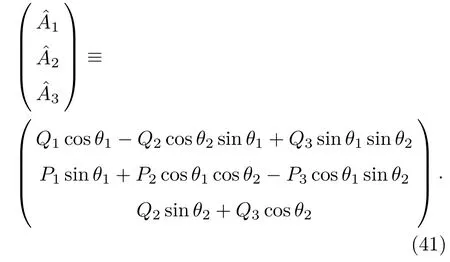
不难看出,(40)式中右边算符是可对易的.由(40)式直接可得本征方程

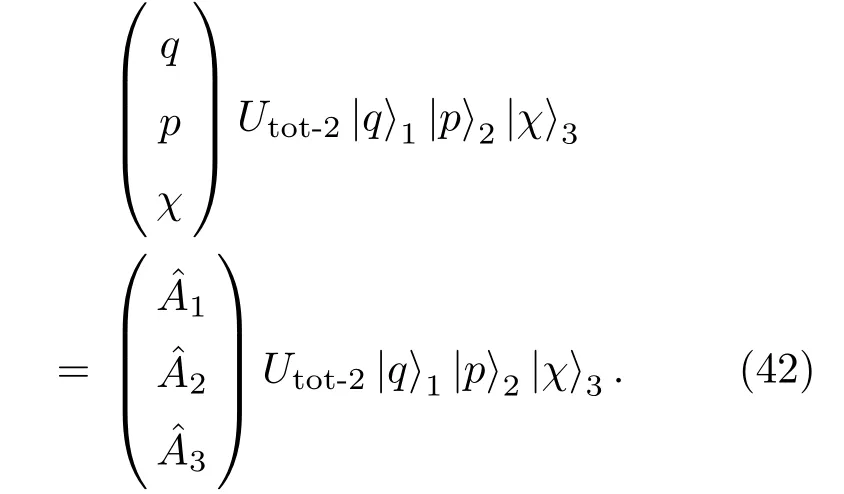
至此,我们构建了一类新形式的三模纠缠态表象,它是正交完备的.这一点可直接由表达式以及坐标态、动量态的完备性关系得到;也可利用有序算符内积分技术将正交性和完备性分别写成

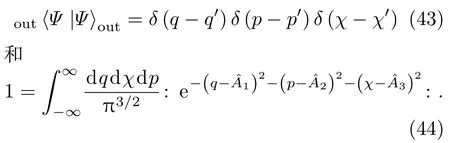
即在正规乘积下,量子态的完备性关系写成了一个高斯型积分.这也为构造量子力学表象提供了一个新的途径.纠缠态表象在其他方面,如构造压缩算符、纠缠分数傅里叶变换以及纠缠分数压缩变换等也有相关应用[2−4].这些将在进一步工作中予以讨论.

4.2 条件测量下输出量子态的计算

实际上,级联光束分离器在量子信息处理、量子态工程中是一种常用的线性器件.结合光子数探测、零差探测等可实现量子CNOT门、非高斯量子态(如压缩类-Bell态)、qubit量子态的隐形传输及量子测量精度的改善等.在图2中,进一步考虑在输出端b2与b3进行光子数探测,a1(a2)与a3分别输入数态|Ψ⟩12与相干态|α⟩3, 那么测量后b1输出端对应于什么量子态呢?实际上,此过程可看成是量子剪切[32].

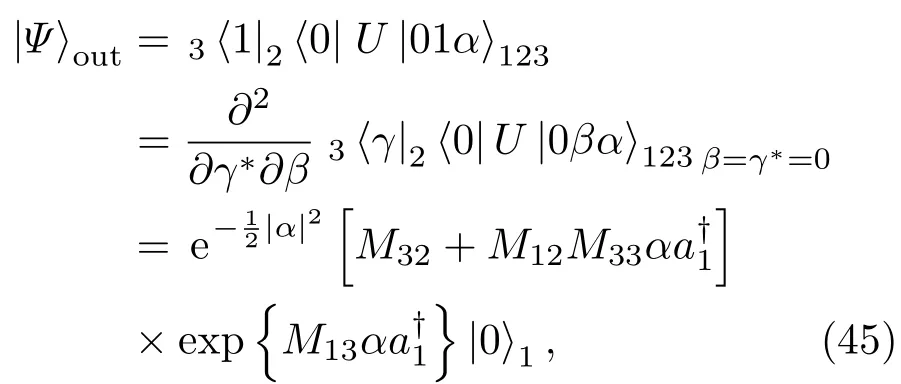
其中Mij为矩阵(23)式的矩阵元.将具体值代入(45)式并令可得归一化输出态为

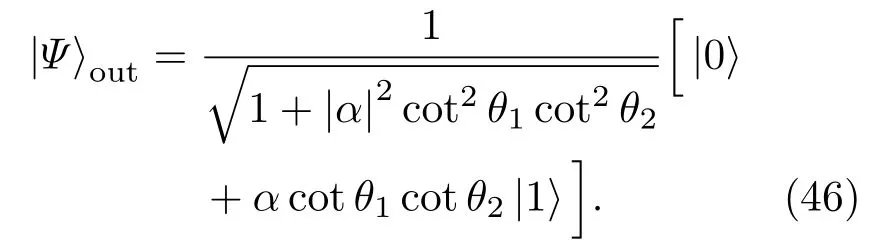
可见,输出量子态中只包含了真空态与单光子态的组合,即相比于输入的相干态而言以上方式实现了相干态的剪切.特别地,当cotθ1cotθ2=1时,输出态为|0⟩+α|1⟩,即留下了与输入相干态的前两项完全相同的项.有趣的是,当第三模a3的输入态为|0⟩+µ|1⟩,不难看出,通过调整两光束分离器的透射与反射率可以获得与|0⟩+µ|1⟩相同的输出态.故该方案也被用于量子隐形传输[22].

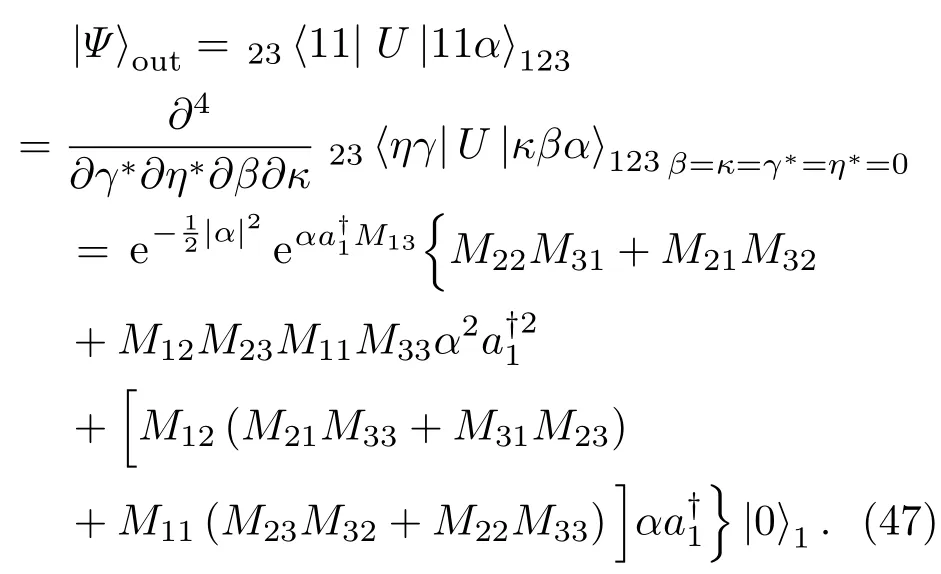
将矩阵元Mij代入后可得归一化的输出态

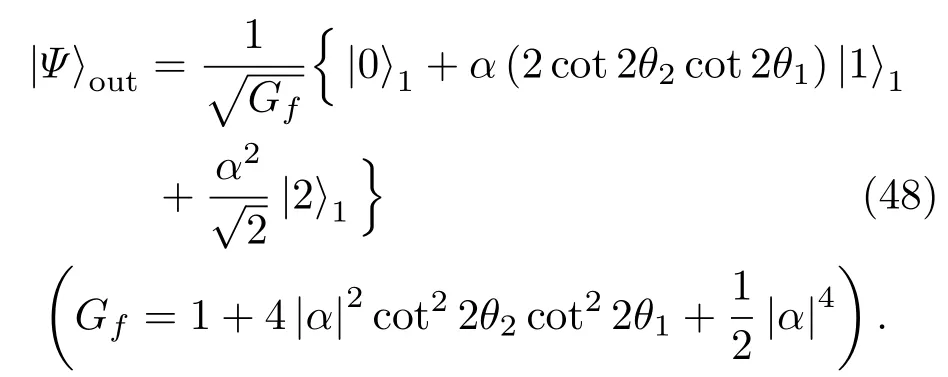
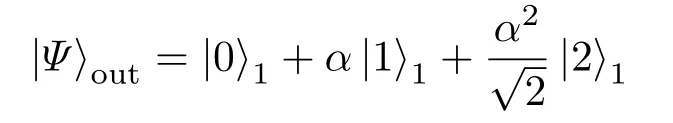
恰好就是相干态的前三项.此外,当cot2θ2=0或cot2θ1=0,有

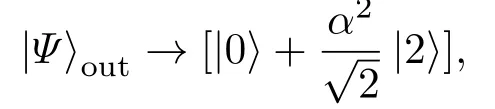
即只要其中一个光束分离器是对称的,则输出态将只包含有|0⟩,|2⟩两个组分.因此,在该方案下,非对称光束分离器是产生以上三组分叠加态的必要条件,且当 2cot2θ2cot2θ1=1满足时,输出态就是输入相干态的前三项.这一结果要求不对称的光束分离器.有趣的是,当第三模输入态为的任意叠加态时,利用上述方案,通过调整光束分离器的透射率,实现完全相同的叠加态的输出是可能的.

5 结 论

光束分离器是一种应用十分广泛的线性器件,其算符的输入输出关系可在Heisenberg绘景中方便地得到,特别是对于由多个线性器件组成的系统,算符输入输出关系可利用单个变换矩阵的乘积直接获得.然而,在诸多情况下,如计算输出端检测到光子数的概率以及获得线性器件对应的幺正算符表示及其表象表示等,则需要转到Schrödinger绘景中来计算输出量子态.基于在Schrödinger绘景和 Heisenberg绘景计算平均值的等价性,建立了Heisenberg绘景中的变换矩阵与 Schrödinger绘景中变换矩阵的关系.具体而言,Heisenberg绘景中湮没算符的变换矩阵转置后就得到Schrödinger绘景中的产生算符的变换矩阵.这一简洁的关系为Heisenberg绘景和Schrödinger绘景变换关系的转换架起了直接的桥梁,即可在Heisenberg绘景中直接给出算符的变换关系,通过转置后直接应用于Schrödinger绘景,而避免了Schrödinger绘景中一步一步的算符变换运算.

基于以上两绘景中变换矩阵的联系并结合有序算符内的积分技术,本文首先给出了单个光束分离器算符在坐标表象中的表示及其正规乘积形式与紧指数表示.此后,进一步考察了两个级联光束分离器算符的表象表示及正规乘积形式与紧指数表示.并推广至多光束分离器的组合情况.相关研究内容为多模纠缠态、多模qubit态的制备提供了一种有效的途径,且为由光束分离器组成的线性器件系统总作用的算符正规乘积及其紧指数表示提供了一般方法.此外,考察了两个级联光束分离器在量子力学表象制备以及条件测量下制备叠加量子态中的应用.利用级联光束分离器的表象表示,不但可以有效地给出纠缠态表象的Schmidt分解,而且可知输入若为非经典的坐标态(压缩无限大的理想态)并不能得到纠缠态.这就意味着,向光束分离器输入非经典态时并不总能获得纠缠态.利用级联光束分离器算符的正规乘积并结合条件测量,可以方便地计算输出量子态,如数态|0⟩,|1⟩,|2⟩的叠加态.本文的处理方法可推广至其他线性器件组成的复杂系统中.今后,将进一步讨论新纠缠态表象在光学变换,如小波变换、分数傅里叶变换中的应用.