用于心脏电活动成像的空间滤波器输出噪声抑制方法∗

周大方 张树林 蒋式勤†

1)(同济大学电子与信息工程学院,上海 201804)2)(中国科学院上海微系统与信息技术研究所,信息功能材料国家重点实验室,上海 200050)(2018年2月6日收到;2018年4月8日收到修改稿)

1 引 言

波束成形方法是一种空间滤波技术.它可以通过构造一个空间滤波器,提取该位置上感兴趣的源强度信息,同时抑制来自其他位置上源的影响[1,2].这种方法采用分布源模型估计分布电流源偶极矩的强度及其空间位置信息,即分布源的空间谱.相比采用单电流偶极子源模型,波束成形方法解决了估计多源的计算问题,可以细致地描述生物电活动,但是,面临如何准确重建多源的问题.近年来,最小方差波束成形(minimum variance beamforming,MVB)[1−7]被用于重建分布等效电流偶极子(equivalent current dipole,ECD)源的研究,例如,识别预激综合征(wolf f-parkinson-white)病人心脏房室的旁路传导[8,9],以及定位房颤(atrial fibrillation,AF)病人的AF病灶[10]和利用磁场图(magnetocardiogram,MCG)仿真数据的心脏轮廓成像[7].在重建磁场分布电流源时,MVB通过自适应的空间滤波技术,最小化空间滤波器输出总功率及归一化噪声空间谱强度,降低了测量噪声对电流源空间谱估计的影响.可以发现,如果在MVB方法的基础上,再针对性地约束空间滤波器输出的噪声功率增益,可以进一步提高分布电流源空间谱估计的源分辨能力,从而增强心脏电活动磁成像的分辨率.

本文提出了一种可抑制空间滤波器输出噪声功率增益(suppressing spatial f i lter output noisepower gain,SONG)的波束成形方法.用一个对空间滤波器输出功率有影响的低迹的半正定矩阵构造一种新的滤波器权矩阵,可以约束空间滤波器的输出噪声功率的增益.该低迹的半正定矩阵满足特征值不大于1,且矩阵的迹小于其阶数.这样,可以提高分布电流源空间谱估计的分辨率.文中通过理论分析和仿真实验比较了SONG和MVB方法.给出了用两个健康人的36通道MCG数据得到的心脏电活动成像.结果表明,SONG方法分辨电流源的能力较强,能够观察到Rpeak时刻健康人的心室内有较强电活动等明显的电生理特征.

2 波束成形方法

2.1 问题的提出

假设第j个单位电流偶极子源的位置和方向分别是rj=(xj,yj,zj)(j=1,2,···,n)和[1,0,0]T,[0,1,0]T或[0,0,1]T.它产生的理想磁场列向量为lX,j,lY,j或 lZ,j,相应的导联场矩阵表示rj处电流源的测量灵敏度.已知心脏磁场的测量数据b(t)[11,12],求电流源偶极矩q(t,rj)的逆问题[13,14],可用线性方程表示[15,16]:

其中,b(t)=[b1(t),b2(t),···,bc(t)]T表示t时刻c个测量通道的磁场向量;v(t)是t时刻的测量噪声向量;等效电流源的偶极矩q(t,rj)=q(t,rj)η(t,rj),j=1,2,···,n, 其中n是电流源的数目.源偶极矩的强度是标量

表示单位向量.rj=(xj,yj,zj)是第j个电流源位置的坐标.下文中,q(t,rj),η(t,rj),q(t,rj),v(t)和b(t)将简写为qj,ηj,qj,v和b.

空间滤波是一种常用的分布源重建方法.将心脏磁场测量数据b(t)作为空间滤波器的输入,估计的分布源的偶极矩作为输出.空间滤波可用加权的线性运算表示:

其中,W(t,rj)是空间滤波的权矩阵.(2)式可简写为

MVB方法的基本原理是先用空间滤波技术重建心脏的分布电流偶极子源.然后,根据可描述电流源偶极矩平均强度的分布电流源空间谱估计,对心脏电流源成像.电流源偶极矩是源电流密度在邻域的体积分,它与该位置上的源电流密度大小,也就是电流源强度有关[13,14].

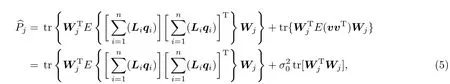
式中,前一项为空间滤波器输出的所有电流源偶极矩qi的功率和;后一项为空间滤波器输出的噪声功率,其中为噪声功率的增益.对开方,可得估计的电流源偶极矩平均强度空间谱:

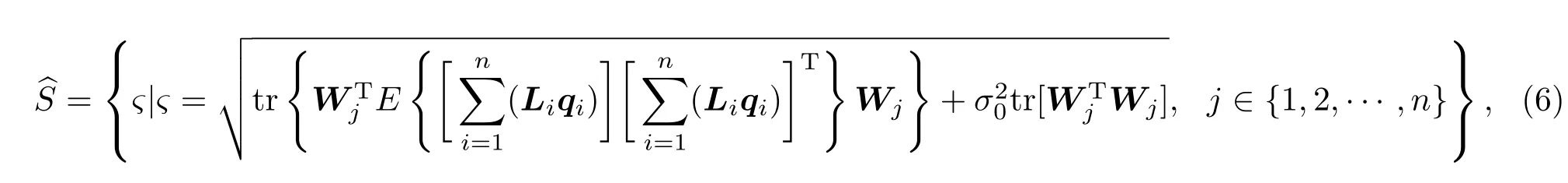
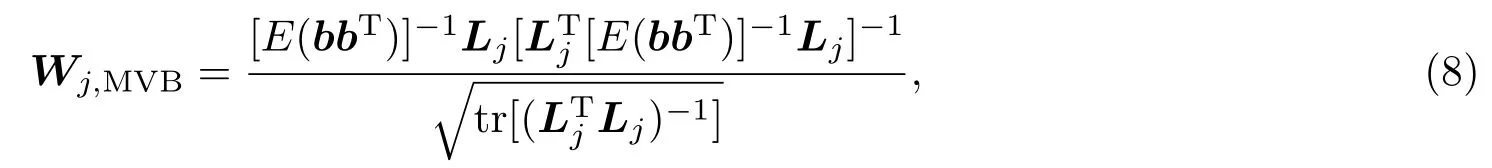
2.2 SONG波束成形方法

本文提出了一种SONG波束成形方法.令空间滤波权矩阵

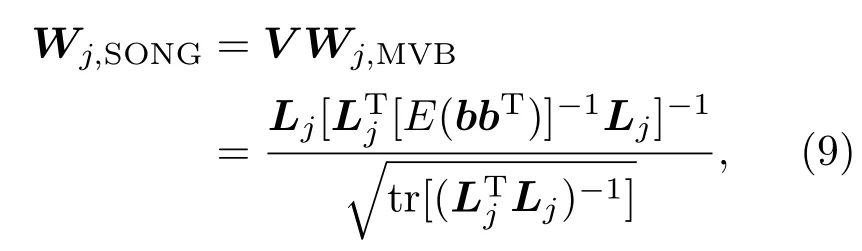
可以证明,其中的c阶实对称矩阵V=E(bbT)是一个对空间滤波器输出功率有影响的半正定矩阵,满足“矩阵的迹低于其阶数,且其特征值不大于1”,(以下简称V是低迹半正定阵).因此,SONG方法中输出噪声功率增益可表示为

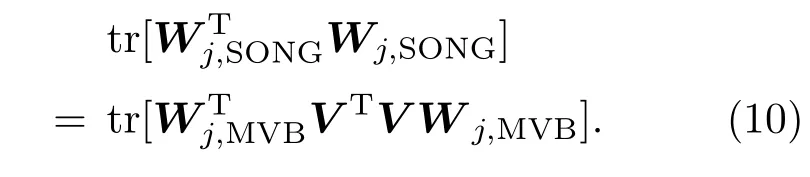
令任意矩阵Γ =Wj,MVB,也可以证明,存在不等式

当V=E(bbT)时,由(10)和(11)式可知

也就是说,SONG方法可以或更好地降低空间滤波器的输出噪声功率增益.将E(bbT)=I代入(8)和(9)式可知,SONG的噪声空间谱强度与MVB相同,均等于1.综上,SONG方法不仅可以约束噪声空间谱对分布源空间谱估计的影响,还可约束空间滤波器输出噪声功率的增益.相比MVB,SONG方法可以提高估计空间谱的分辨率.

2.3 SONG方法的分析与比较

采用波束成形方法,电流源的空间谱估计决定了电活动成像的分辨能力.由于多电流源重建问题比较复杂,本文比较了SONG和MVB单电流源重建的源分辨率.

由(2)式可知,当单电流源偶极矩方向已知时,空间滤波器的源偶极矩估计可以退化为源偶极矩的强度估计是退化后空间滤波器的权向量.由(7)式可知,单源在任意位置上产生的估计空间谱强度为假设单源S位置rs上的估计空间谱强度为b ςs.为了分析估计空间谱的单源分辨率,定义任意位置rj(j=1,2,···,n)上的点扩散函数(point spread function)为(rj)[4],可用归一化后的估计空间谱强度简单表示为

由(9)式可知,单源重建时,SONG方法的权向量为

式中,

其中,lj是电流源产生的磁场列向量.

由(7)和(13)式可得SONG方法估计的空间谱

其中

将(15)和(17)式代入(14)式,可得SONG方法在任意位置rj(j=1,2,···,n)的估计空间谱强度

归一化后的点扩散函数为

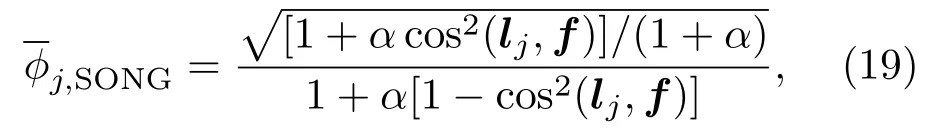
同理可得,MVB单源重建的估计空间谱强度和归一化后的点扩散函数

比较(19)和(20)式,有

通常,所有测量通道上的理想磁场信号平均功率大于噪声平均功率[11,12].所以,可令α=根据施瓦兹不等式性质,可知由此,从(20)和(21)式可以得到

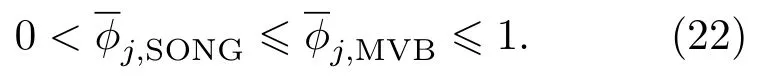
可见,当rj=rs时,单源位置上点扩散函数和相等,为最大值1. 当rj̸=rs时,其他空间位置上,SONG方法的点扩散函数比MVB的小.点扩散函数ϕj可以反映单源对空间其他位置的估计空间谱强度影响大小(rj̸=rs)的取值小,说明单源对邻域的影响扩散小.因此,相比MVB,SONG方法对单源的空间分辨率较高.

3 仿真与实验

3.1 仿真数据和结果

相关电流源(correlated sources)是比较难分辨的,所以,文中利用仿真的磁场数据,比较了SONG与MVB方法估计相关电流源的能力.

假定躯干G0={(x,y,z)|x∈[−12.5,12.5],y∈[−12.5,12.5],z∈[3,20]}(cm).随机给定两个相关源的位置坐标为(6.5,−2.5,11)和(−2.5,6.5,11)(cm),它们的相关系数为0.9824.G0被划分为间距1 cm的10625个体素(voxel).并用ECD源模型产生两组仿真的36通道Z轴测量磁场数据,采样频率为1 kHz[7,12],如图1(a)和图1(b)所示.假设其中测量噪声分别为根均方(root-mean-square,rms)信噪比(signal-to-noise ratio,SNR)20 dBrms和10 dBrms的高斯白噪声[7,12].产生仿真的磁场数据和进行电流源空间谱估计,都要用到等效电流源的导联场矩阵.文中采用水平分层导体作为躯干模型,并通过解磁场的正问题求导联场矩阵[7,13,14].

图1(c)和图1(d)是SONG和MVB在XY平面(z=11 cm)上归一化后的空间谱估计强度的等高线图,等高线的步长为1%.结果表明,SNR对相关电流源的空间谱估计有影响.与MVB相比,用SONG方法估计的相关源强度比邻域的估计源强度有明显的增强.MVB方法中,表示滤波器的输出噪声功率增益,本文在此基础上给出了SONG与MVB方法的输出噪声功率增益比

如图1(e)和图1(f)所示.其中,横坐标是分布源位置的索引,纵坐标是增益比β.将(12)式代入β可知β>0.当β>0时,说明SONG方法抑制噪声的效果比MVB好.图1表明,测量信噪比SNR分别为20和10 dB时,用SONG重建相关源时,滤波器输出噪声增益比β分别为584—622和592—623.在SNR=10 dB时抑制噪声增益的效果较SNR=20 dB时更明显.因此,图1(c)和图1(d)表明,SONG方法有较强的相关源分辨能力,并且在SNR较低时,其源分辨能力更加明显.

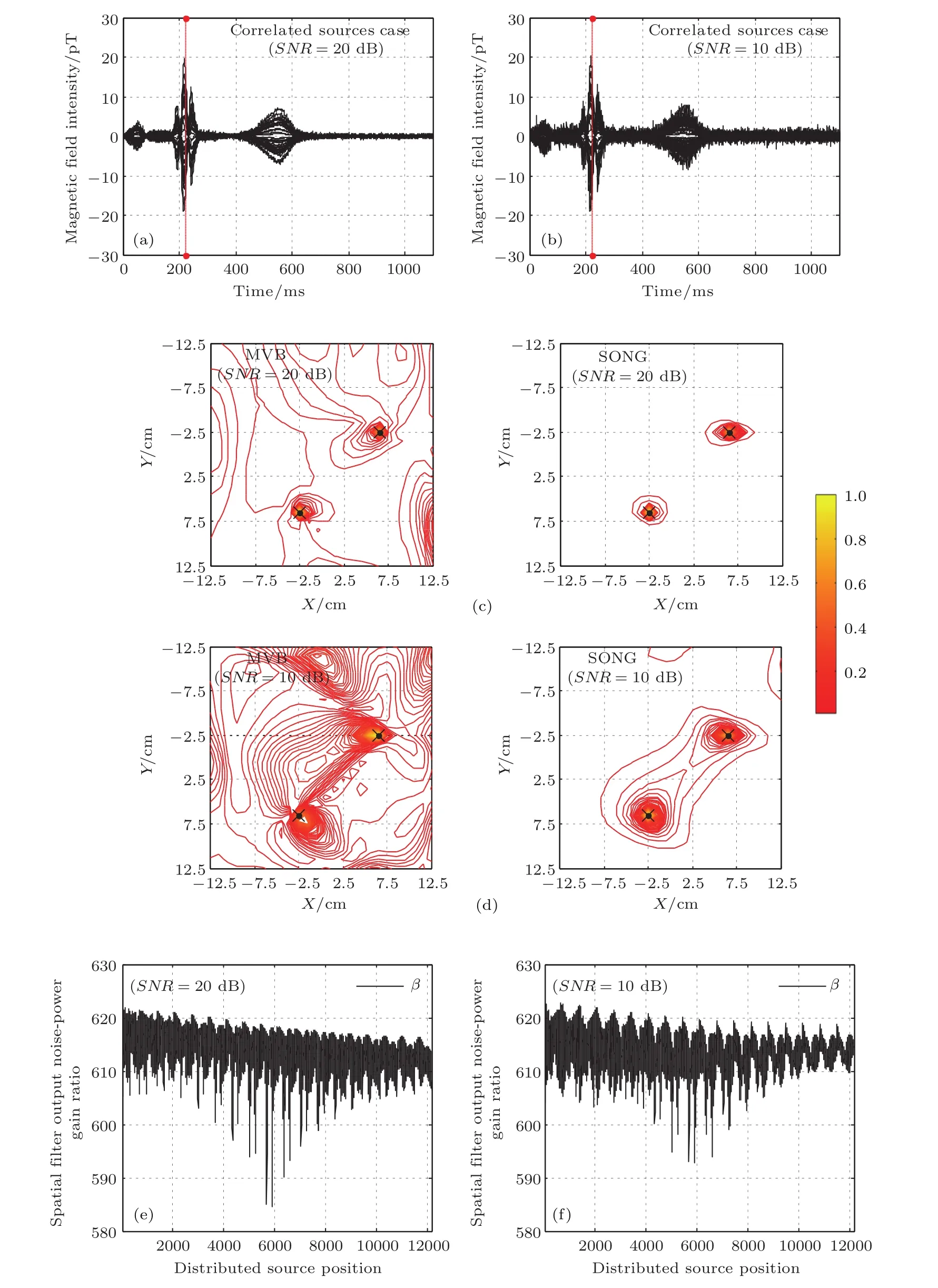
图1 (a),(b)两种SNR情况下,两个相关电流源产生的仿真磁场数据(红色虚线表示重建相关源的时刻);(c),(d)SONG和MVB在XY平面(z=11 cm)上估计空间谱强度的等高线图(×号表示相关源的给定位置);(e),(f)用SONG方法的空间滤波器输出噪声功率增益比βFig.1.(a),(b)Simulated magnetic data generated by two correlated current sources with noise,respectively.The red dashed line denotes the time of source reconstruction.(c),(d)Estimated spatial spectrum intensity contour on XY plane(z=11 cm)using SONG and MVB.The black cross signs×denote the given locations of two correlated sources.(e),(f)Ratio β of noise-power gain of spatial f i lter output using SONG method.

3.2 心脏电活动成像

分布电流偶极子源的偶极矩强度可以反映分布电流的强度,因此,可利用分布源空间谱估计的强度对心脏电活动成像.文中还用两个健康人的心脏磁场数据比较了SONG和MVB成像的效果.在求导联场矩阵时,采用水平分层导体作为躯干模型[7,13,14].用这种模型时,导体边界上的单位法向量均平行于心脏测量磁场的单位向量,所以,求解导联场矩阵时,躯干体电导的影响可以忽略[7,13,14].

图2是沿Z轴测量的两个健康人的36通道单周期心脏磁场曲线.测量平面为25 cm×25 cm.36通道的SNR约为10—20 dB,带宽0.01—100 Hz,采样频率1 kHz[12].

图2中心脏磁场信号的Rpeak时刻对应心室的除极期.这时健康人心室电活动较强,心房的相对较弱[17],比较容易识别[11,12].因此,文中比较了SONG和MVB两种方法的成像结果.将测量平面与健康人核磁共振影像(magnetic resonance imaging,MRI)的心脏冠状位(coronal view)、水平位(transverse view)和矢状位(sagittal view)图的坐标配准,然后,用MRI中心脏的位置作为房室位置的参考.图3(a)和图3(b)给出了归一化后的分布源空间谱估计强度的等高线图.其中,冠状位视角的XY面(z=10 cm)、水平位视角的XZ面(y=2.5 cm)和矢状位视角的Y Z面(x=0.5 cm)的交点(0.5,2.5,10)cm位于心室内,用蓝色的小方框表示,谱强度等高线的步长为1%.图3(a)和图3(b)表明,SONG方法的成像结果能够反映健康人Rpeak时刻电活动的特征.因为Rpeak时刻,健康人的心房除极已结束,心室正处于除极期.根据图中色标,可以观察到心室内黄色表示的电活动强度明显比心房内红色表示的电活动强度高,以及心室邻域的电活动相对较强[7,11,12,17,18].由于SONG增加了心脏内外分布源空间谱估计强度的差异,心脏分布电流源的分辨率提高了.用MVB的成像结果相对模糊,特征不明显.

图3(c)和图3(d)的结果表明,Rpeak时刻用SONG方法,两个健康人的滤波器输出噪声增益比β分别为206—228和215—232.也就是说,当实测心磁数据SNR为10—20 dB时,相比MVB,SONG能够更好地抑制空间滤波器输出噪声.如图3(a)和图3(b)所示,SONG方法的源分辨能力以及成像效果相对较好.

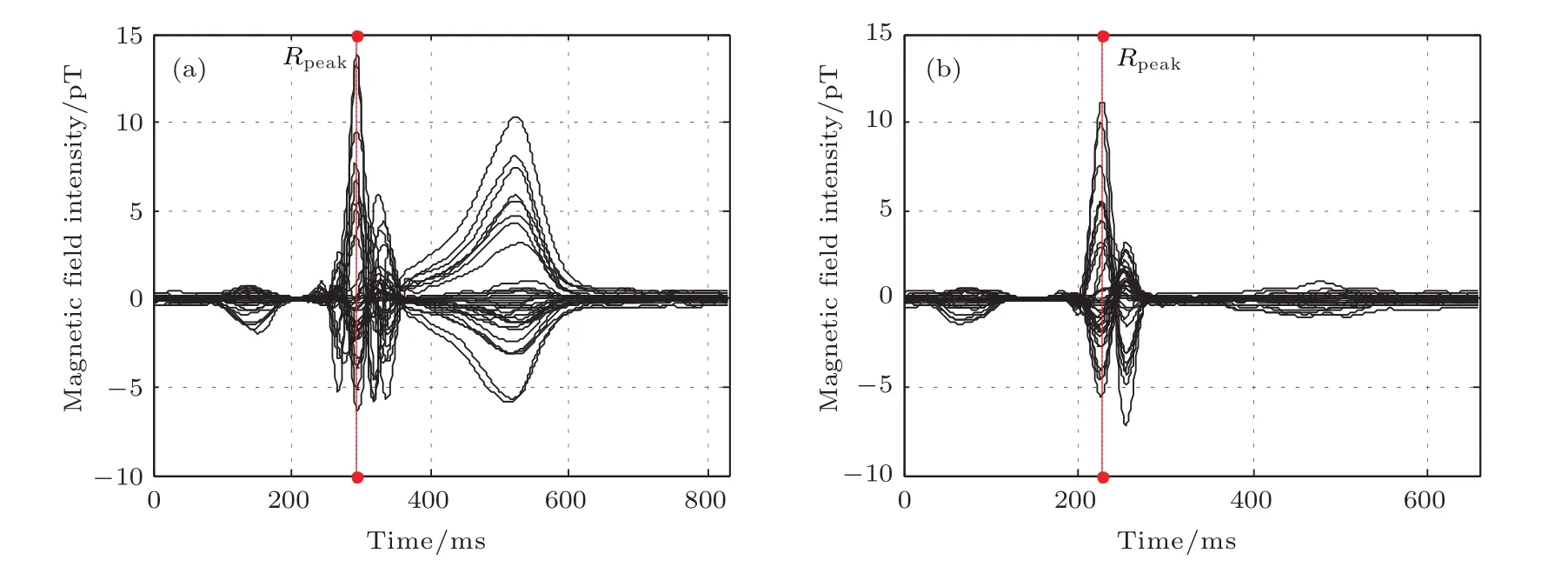
图2 (a),(b)两个健康人的36通道单周期心脏磁场数据及对应的Rpeak时刻Fig.2.(a),(b)The 36-channel MCG data of single-cycle from two healthy subjects,as well as the time-points of Rpeakfor MCG imaging.

4 讨 论

由(12)式可见,SONG波束成形方法可以约束空间滤波器输出噪声的功率增益.用构造滤波权矩阵Wj,SONG类似的方法,还可以构造其他的滤波权矩阵.虽然理论上其他空间滤波权矩阵对应的噪声空间谱强度也恒等于1,并可以约束空间滤波输出噪声功率增益,但是,仿真结果表明,其他滤波权矩阵会使两个相关电流源定位到它们的中间位置.因此,必须利用测量信号的二阶特征矩阵E(bbT)构造空间滤波权矩阵[2,7].因为测量信号矩阵E(bbT)可以反映电流源的相关性.图1中用SONG方法,两个给定的相关源可以准确定位.

我们还利用MCG仿真数据,研究了重建分布源的最小范数空间滤波(minimum norm spatial f i ltering,MN)方法[19,20],这种非自适应的空间滤波方法,采用了Tikhonov正则化技术.仿真结果表明,有可利用的心脏三维轮廓时,MN的分布电流源成像结果较好[19].参考文献[19]的图3和图4给出了重建的16个等效电流源,与本文图3中SONG方法的成像结果类似.

图3 (a),(b)两个健康人的分布源空间谱估计强度的等高线图;(c),(d)两个健康人的空间滤波器输出噪声功率增益比βFig.3.(a),(b)Contour of the estimated intensity of distributed source spatial spectrum of two healthy subjects;(c),(d)spatial f i lter output noise-power gain ratio β of two healthy subjects.

5 结 论

本文在研究MVB方法的基础上,提出了一种用于心脏电活动成像的可抑制空间滤波器输出噪声功率增益的波束成形方法.该方法利用一种低迹半正定矩阵构造了一个滤波器权矩阵,可以降低空间滤波器输出的噪声功率增益,提高重建分布电流源偶极矩强度分辨率即分布电流源空间谱估计的源分辨能力,从而增强心脏电活动磁成像的分辨率.仿真实验和分析比较的结果表明,SONG方法优于MVB方法.当心磁信号的SNR不低于10 dB时,采用该方法可以提高心脏电活动成像的效果,将有助于相关的医学研究和应用.

感谢中国科学院上海微系统与信息技术研究所的张懿教授、谢晓明教授和孔祥燕教授及其团队为本研究提供可用的心脏磁场数据与核磁共振影像数据,以及有关的技术交流.