基于模糊神经网络的简支板结构振动控制研究

缑新科 刘 彬

（1.兰州理工大学电气工程与信息工程学院 兰州 730050）

（2.甘肃省工业过程先进控制重点实验室 兰州 730050）

关键字 PLZT作动器；模糊神经网络控制器；振动控制

1 引言

新型光电材料锆钛酸铅镧改性陶瓷（PLZT）是在PZT陶瓷基础上掺杂一定量镧元素然后按照一定比率有机结合而成的透明铁电材料，它同时具备了传统压电材料、热释电材料和铁电材料的所有特性［1］。但不同与传统铁电材料的是，PLZT陶瓷可以在其反常光生伏特效应和逆压电效应的共同作用下产生光致伸缩应变，即当外部有特定波长的高能光束均匀照射在由铁电陶瓷PLZT制成的光致伸缩作动器表面时，PLZT作动器会沿着其极化方向上产生光致应变，有效避免了传统铁电材料受复杂电磁场和高电压设备的影响，可以作为一种理想的非接触式作动器，在层合柔性结构的主动振动控制领域中具有良好的应用前景。近年来，国内外许多学者对PLZT陶瓷的组成成分、性能和应用进行了一系列研究：Tzou等首次提出将二维分布式光致伸缩作动器应用于平面板的模型［2］，并研究分析了作动器基本参数对板结构的影响；Shih等将分布式PLZT作动器层合在二维平面板结构上［3］，分析了作动器在不同分布条件下对结构低阶模态的控制效果；Shih和Tzou等也对PLZT作动器在复杂柔性结构的半球壳和抛物壳振动控制中的空间布局优化提出了建设性意见［4］。而在国内，研究学者对于光致伸缩作动器的研究工作起步相对较晚：陈德金利用遗传算法对层合简支板的作动器布局进行优化［5］，同时设计了基于遗传算法优化权值矩阵的LQR最优无线主动控制算法；岳洪浩提出了一种新的多自由度PLZT作动器模型［6］，为其层合应用于结构振动控制领域提供了更多的构型设计；贺容波设计了模糊滑模变结构控制器［7］，对作动器最优光照切换面方向进行讨论，实现了光电层合板的振动控制。

但目前，关于光电层合柔性结构的振动控制研究大部分是以最优控制、速度比例反馈控制和遗传控制等经典控制算法为主的［8］，智能控制算法较少得以研究应用。模糊控制和神经网络控制是当前智能控制领域中应用较为广泛的控制方法，两者都不需要控制系统有精确的模型，是用一种不确定的方法来处理控制系统的信息。因此，本文将以层合简支板为例，提出利用模糊神经网络控制算法研究光电层合简支板的系统结构振动控制问题。首先，建立了光电层合简支板的动力学模型，推导出层合简支板的振动方程和模态控制方程；然后将模糊控制设计思想与神经网络控制方法相结合设计了基于RBF神经网络模型的模糊神经网络控制器及其相关参数学习调整方法；最后运用Matlab对层合简支板结构进行振动控制仿真，从而验证模糊神经网络控制算法对层合简支板振动控制的有效性。

2 简支板结构的振型方程

将两对光致伸缩作动器分别对称粘贴在柔性简支板结构的上下表面，如图1所示。设层合简支方向的光致伸缩作动器1的位置由坐标x1，x2，y1，y2确定，以沿 y轴正方向为极化方向的作动器2的位置由坐标x3，x4，y3，y4确定。当外部高能冷光源均匀地照射在作动器表面时，光致伸缩作动器会在其极化方向上产生应变和弯矩作用。根据材料力学知识可得到作动器1在层合简支板结构上产生的弯矩控制力表达式为

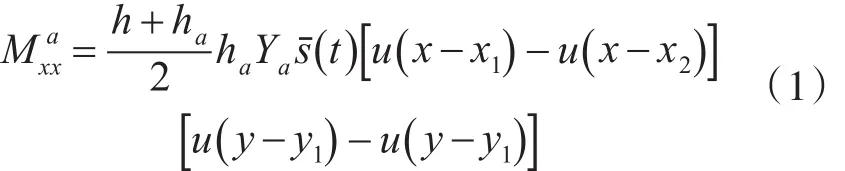
同样，以y轴正方向为极化方向的作动器2产生的弯矩控制力为

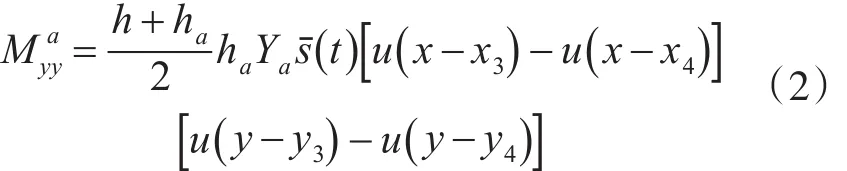
其中Ya为简支板杨氏模量，ha，h分别为简支板和作动器片的厚度，u()为单位阶跃函数。

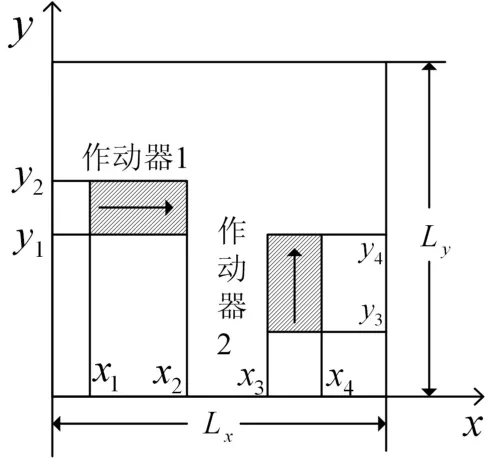
图1 光电层合简支板

在实际的控制应用中，弹性板结构的振动主要是以弯矩作用产生的横向振动为主的［9］，所以在研究分析层合结构振动控制过程中，忽略光致伸缩作动器的平面薄膜力和弯曲效应对层合简支板的影响，故层合简支板的振动方程可表示为

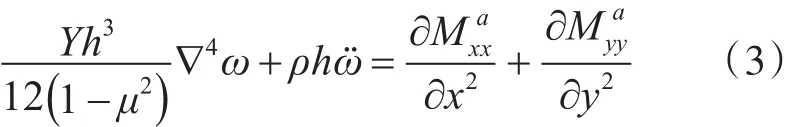
根据机械振动理论，将简支板固有振动形式展开成双重级数形式为

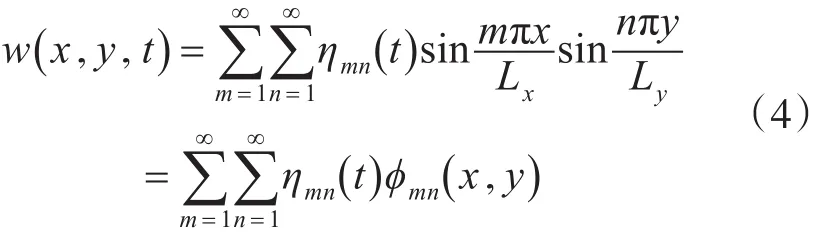
其中ϕmn(x 。y)为正则振型函数。将简支板的固有振动形式式（4）代入到简支板的振动方程式（3）中，并运用模态正交性推导得到简支板的模态控制方程为

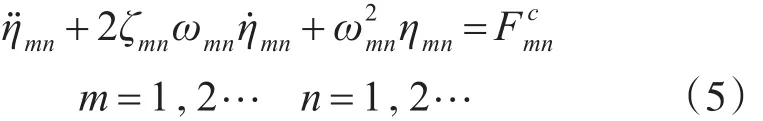
式中ηmn为mn阶模态的幅值，ωmn为mn阶模态的固有频率，Fcmn为模态控制力，可表示为

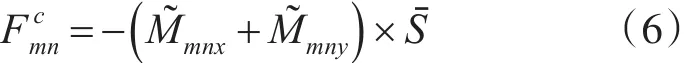
式中M~mnx，M~mny分别表示为x轴方向和 y轴方向的弯矩控制因子，可表示为

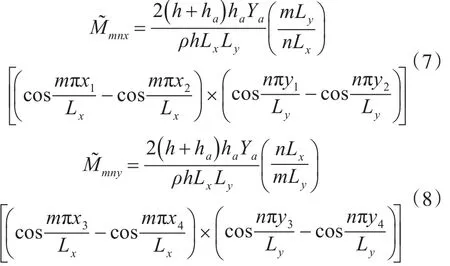
简支板的固有频率为

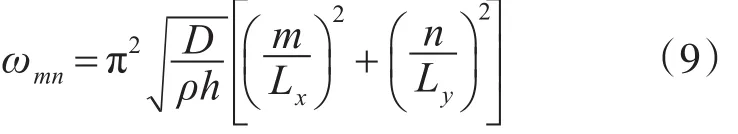
Sˉ表示为PLZT光致伸缩作动器产生的光致应变，其表达式为

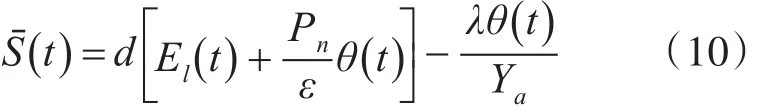
其中El(t)为光生电场，θ(t)为光生温度，Pn为热释电常数，ε为介电常数。

3 模糊神经网络控制系统

图2为光电层合简支板模糊神经网络控制系统结构框图。模糊神经网络控制器的设计原则是将模糊控制设计思想引入到多层前向RBF神经网络控制系统中去，二者相结合，将模糊控制输入变量的模糊化处理、模糊推理、精确化计算用分布式的神经元节点来表示。以模态位移ηmn和模态速度η˙mn作为模糊神经网络控制器的输入，以控制信号u作为控制器的输出来控制光强的大小和方向。模糊神经网络融合了模糊控制和神经网络控制两者的优点，不仅具有处理模糊信息的能力，又具有神经元网络的自学习，自调整的能力。

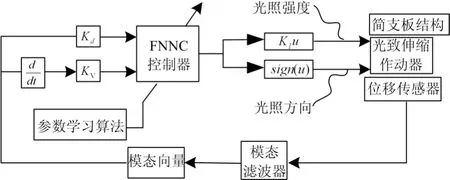
图2 光电层合简支板系统控制结构框图

3.1 模糊神经网络设计

在模糊神经网络控制结构中，以模态位移ηmn和模态速度η˙mn为变量作为模糊神经网络控制器的输入，以控制信号u作为控制器的输出。根据常规二维模糊控制器的设计原则［10］，首先将输入变量模态位移ηmn和模态速度η˙mn分别乘以各自的量化因子转换到相对应的论域范围内，设两个模糊输入变量的基本论域为［-3，3］，对应的模糊语言可标示为“负大”、“负中”、“负小”、“零”、“正小”、“正中”、“正大”7个模糊子集，即｛NB，NM，NS，ZO，PS，PM，PB｝，如图3所示模糊神经网络的模糊层共有14个神经元节点。基于模糊控制器的设计，输入变量模糊子集的隶属函数均采用高斯函数形式，则模糊层第i个神经元节点的输入输出可表示为

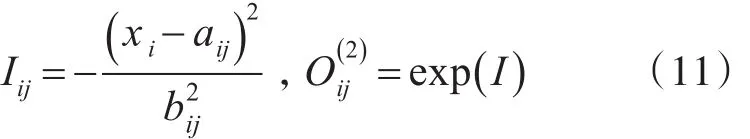
式中aij和bij分别表示为第i个输入变量的第j个模糊语言值隶属函数的中心和宽度，且i=1。2，j=1。2…7。

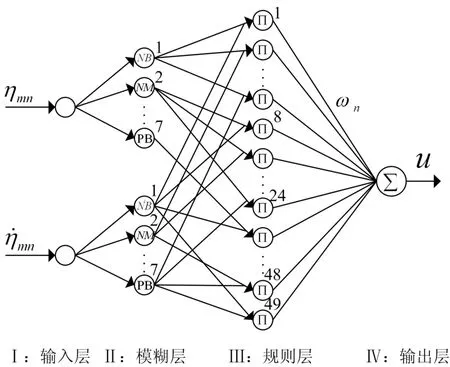
图3 基于RBF网络模型的模糊神经网络控制结构图

模糊层每一个神经元节点的输出作为规则层的输入，然后通过乘积运算后输出作为控制结构输出层的输入，由于两个输入变量都有7个模糊语言集合，则FNNC控制器相应的模糊推理规则有7*7条。在图3所示规则层中，若每一个神经元节点代表一条模糊推理规则，则规则层一共有49个神经元节点。因此规则层第m个神经元节点的输入输出可表示为

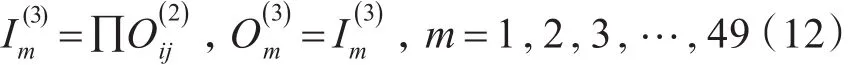
而输出层的输出是控制结构图中规则层的所有神经元节点相互作用后的结果作为输出。将规则层每个神经元节点的输出通过一定线性组合然后作用求和，其结果作为输出层的输入，同时采用精度较高的面积重心法去模糊化，则输出层的输入输出可表示为

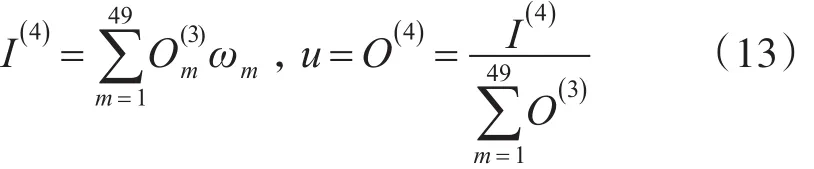
3.2 FNNC参数学习算法

在控制设计过程中，控制系统需要更新修改的参数是模糊神经网络控制结构的模糊子集高斯隶属函数的中心aij、宽度bij和控制结构中输出层连接权值系数ωn。从图3所示控制器结构图来看，模糊神经网络控制结构是可以视为一种类似于多层前向BP神经网络的感知器结构，因此控制器输出层连接权值系数ωn的调整可以利用BP神经网络的误差反向传播的权值调整思想。当神经网络系统输出与期望输出存在一定误差时，误差E表达式为

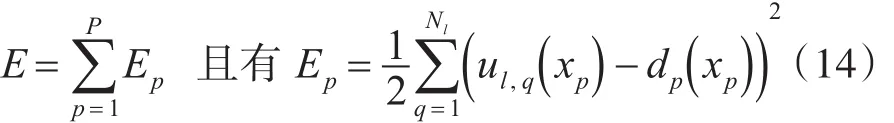
对于一个三层神经网络结构，将偏差定义推导到隐含层：

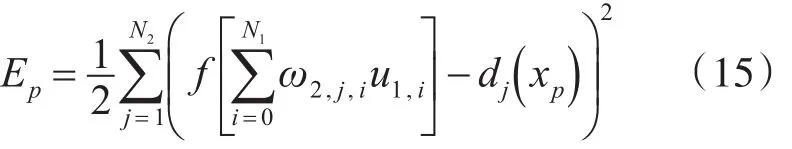
再进一步将隐含层表达式（15）展开至输入层：

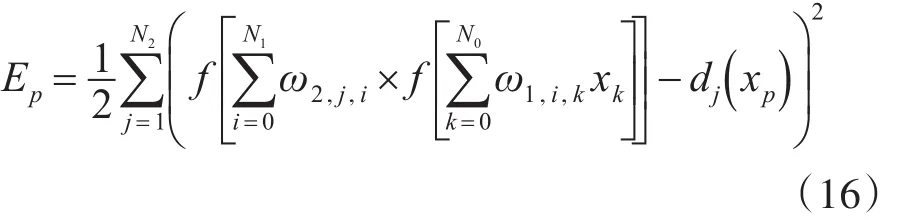
从式（16）可以看出：系统输出偏差与神经网络各层间连接权值系数有关，通过调整权值系数的大小可以改变系统输出偏差。为了满足系统输出偏差尽可能小的要求，需要对权值系数不断地进行调整，使其调整量与偏差的梯度下降成正比，则权值系数的调整方法为

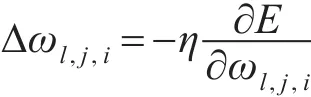
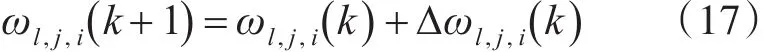
其中ωl。j。i为神经网络各层间连接权值，η为学习率。

一般情况下，神经网络学习率的取值直接影响着神经网络系统的收敛速度和稳定性［11］。为了使神经网络系统有稳定的收敛速度，需要对式（17）增加一个惯性项，以此保证神经网络系统每次调整的方向都与上一次调整方向相一致，同时也降低了偏差函数陡变造成的误差，则权值更新公式为

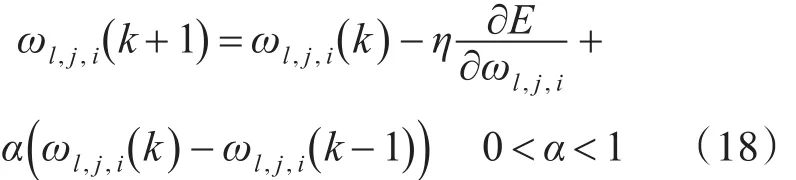
即调整后的连接权值表达式为

同样可以得到高斯隶属函数的中心和宽度的更新表达式为

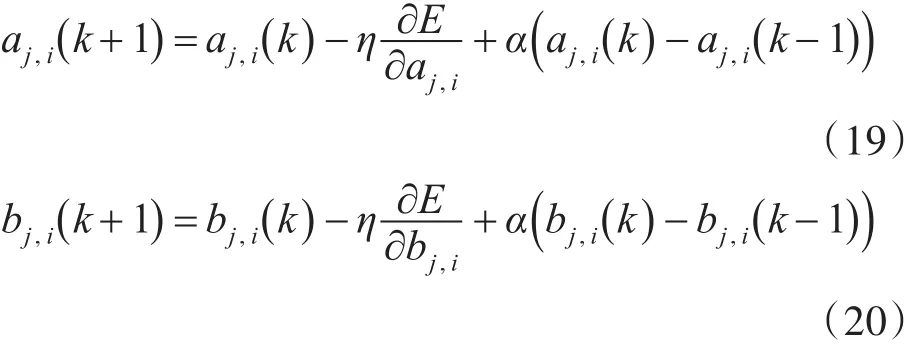
4 数值仿真

以光电层合简支板为研究对象，验证上述控制策略的有效性。受控简支板的尺寸参数为：长Lx=0.6m，宽 Ly=0.4m，高h=0.003m；材料属性为：杨氏模量 Ya=6.3×1010N/m2，密度 ρ=7.8×103kg/m3；在板的上下表面同位对称粘贴PLZT光致伸缩作动器，如图1所示，作动器尺寸参数为0.24m×0.06m×0.0004m，根据文献［5］作动器在板结构的优化位置分布：x1=0.05m。x2=0.29m。y1=0.24m。y2=0.3m 和 x3=0.34m。x4=0.4m。y3=0.06m。y4=0.3m。假设初始时刻t=0s，初始位移为4mm，且不考虑层合结构阻尼，模糊量化因子分别取为 Kd=4×103，Kv=200，FNNC控制器参数学习因子均取为η=0.3，动量因子α=0.001。在Mat⁃lab仿真环境下，对光电层合简支板进行振动控制的数值仿真［12］。图4和图5分别描述了未控制时和模糊神经网络控制时层合简支板的前两阶位移响应曲线。从仿真图可以得到：相比较未控制时，采用模糊神经网络控制能够有效地抑制简支板的振动，减振效果比较明显并且达到稳定所需的时间也有较大幅度的缩短。

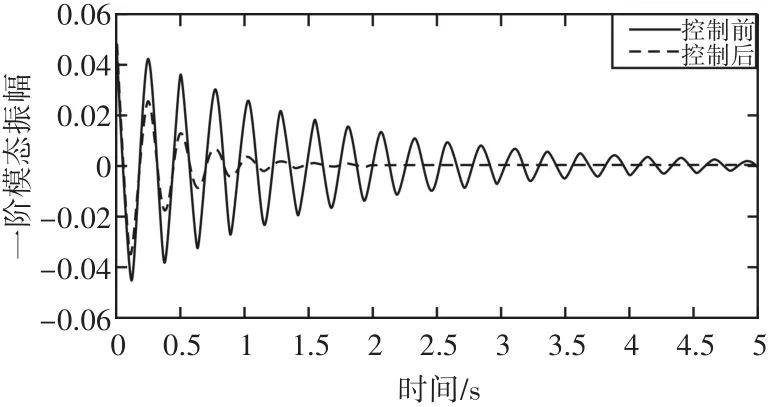
图4 层合简支板一阶模态位移响应

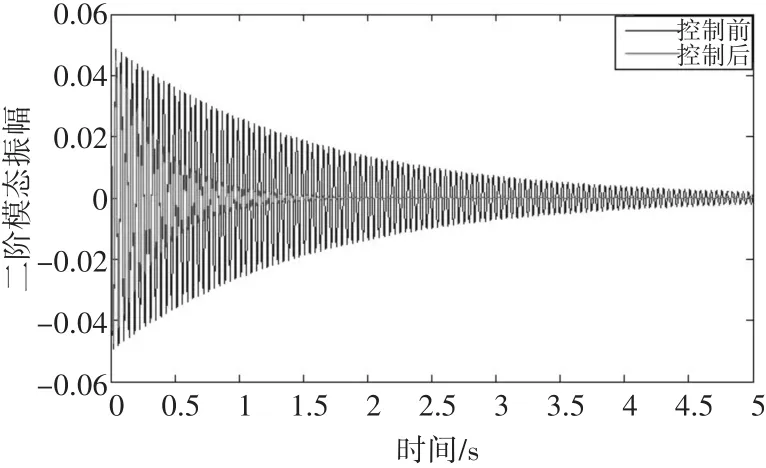
图5 层合简支板二阶模态位移响应

5 结语

针对光电层合结构的系统模型不确定和光致伸缩作动器的非线性特性等问题，本文提出并设计了模糊神经网络控制方法对层合简支板的振动控制进行研究。数值仿真结果表明：模糊神经网络控制算法是有效可行的，能够实现对层合简支板的振动控制，控制效果明显，是一种优于模糊控制单独使用的控制技术，同时也为更多智能控制方法应用于光电层合柔性结构的振动控制领域中提供了一个新的思路。