滑动销与基板过盈配合的微小型火药作动器

解赛鹏，张继豪，陈润亭，吴青云，代 俊

(1.北京理工大学机电工程与控制国家级重点实验室，北京 100081；2.北京理工大学机电学院，北京 100081；3.北京市海淀实验中学，北京 100037)

0 引言

随着引信技术和MEMS技术的发展，武器系统对作动器性能指标提出了更高的要求。微小型作动器是一种重要的执行机构，主要功能是实现力(包括扭力)或位移(包括线性位移和角位移)的输出，是微型机电系统的重要组成部分[1]。微小型作动器是微机电系统内重要的激励响应、能量转换、运动与力传递装置[2]。微作动器与微型传感器、信号处理和控制电路等共同构成微型器件、微型机械或微型系统。传统作动器在结构上大多采用圆筒式结构[3-5]，作动器可动部件在液压、气压、电磁、弹簧等驱动力的作用下与筒体发生相对运动，实现作动器动作。根据工作原理的不同，可将微小型作动器分为静电型作动器、电磁型作动器、压电型作动器、电热型作动器、火药型作动器等[6-7]。火药型作动器是一种通过电能引燃火药，并利用火药燃气压力做功的驱动器，具有尺寸小、能量密度高、作用迅速、驱动位移大等优点。传统圆筒式火药作动器可以将火药中的化学能瞬时转变为机械能，然而，传统的火药作动器需要设计可动元件的定位结构，不利于作动器的工程化实现。

针对上述问题，本文提出了一种通过过盈配合的装配方式实现作动器可动元件动作前后定位的火药作动器，以简化传统火药作动器结构。设计的火药作动器依靠过盈配合的装配方式实现作动器可动部件动作前后的定位。过盈配合联结具有结构简单、定心性好、承载能力高，承受变载荷和冲击的性能好等优点[8]。

1 传统作动器可动元件定位形式

图1(a)所示为一种传统形式火药作动器，火药作动器工作过程可以分为点火过程(点火器装置工作点燃主装药)、挤进过程(气体压力达到一定程度将剪切销剪断)和运动过程(活塞在燃气压力作用下运动)[5]。火药作动器的电起爆器通电发火，燃烧后产生的高温高压气体通过壳体传火孔进入组合件密封壳体腔内，气体压力作用在活塞上，使剪切销被剪切断，活塞沿轴线方向回缩，完成释放功能。图1(b)所示为一种常见的作动器闭锁机构形式，通过卡座弹性梁发生弹性变形，卡入卡头内侧，实现对作

图1 传统作动器可动元件闭锁形式Fig.1 The locking form of the movable element of the traditional actuator

动器可动元件的锁定[9]。传统火药作动器通过剪切销、弹性闭锁机构等实现作动器可动元件的定位，结构较为复杂。本文提出的微小型火药作动器依靠过盈配合的装配方式实现作动器可动部件动作前后的定位，简化了火药作动器结构。

2 滑动销与基板过盈配合的微小型火药作动器

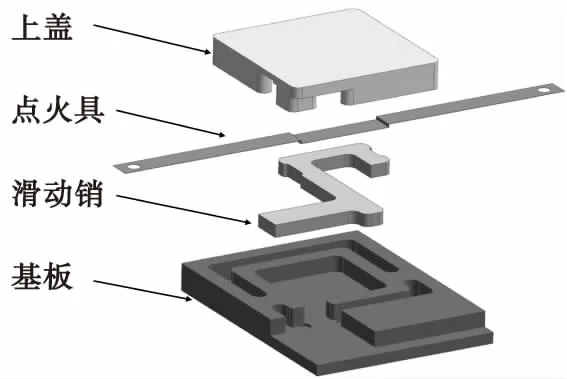
图2 微小型火药作动器Fig.2 Miniaturized propellant actuator

本文采用斯蒂芬酸铅(LTNR)作为作动器的含能材料。如图3所示为作动器相关尺寸参数，l1为基板槽宽度，l2为滑动销宽度，双边过盈量δ=l2-l1，h0为滑动销高度。当作动器火药反应室容积固定后不同装药量对应着火药产生不同火药推力，不同作动器装配过盈量对应着滑动销运动到位(1 ms运动时间)所需最小推力。因此，可以通过寻找过盈量与滑动销运动到位所需最小推力之间的关系以及装药量与火药推力之间的关系实现对过盈量与装药量之间关系的确定。下面本文将分别对过盈量与滑动销运动到位所需最小推力之间关系以及装药量与火药推力之间的关系进行理论分析。

图3 作动器基本尺寸参数Fig.3 Basic parameter of actuator

3 过盈量与装药量对应关系分析

过盈量与装药量直接影响作动器安全性与动作可靠性，定量分析两者之间的对应关系对指导作动器设计具有十分重要的意义。本章节依次对装药量与推力之间关系和过盈量与推力之间关系进行了分析。

3.1 装药量与推力分析

作动器发火药量与相应过盈量是作动器设计的重要参数，决定着微小型火药作动器的安全性与工作可靠性。在过盈量一定的情况下，若装药量过大则会导致作动器爆炸，若装药量过小则不能有效推动滑动销运动到位。因此，需要求出作动器过盈量与装药量之间的关系，在保证作动器可靠工作的条件下减少火药用量，增强作动器的可靠性、稳定性和安全性。要获得过盈量一定时的最小装药量，需建立火药质量与滑动销推力之间的关系。

本文假设燃气服从气体状态方程、火药燃烧遵循几何燃烧定律、燃烧产物成分始终不变、点火药瞬时燃尽、滑动销在燃烧压力推动下的启动是瞬时完成的、忽略原空腔内气体对燃烧反应的影响、忽略热损失、忽略装置形变和不计气体损失以简化计算过程。由气体质量状态方程组式(1)可得作动器装药量与火药推力之间的关系[10]。

(1)

式(1)中，P为火药反应区气体压力，V为火药气体所占容积，m为装药量，f为火药力(作动器使用的斯蒂芬酸铅火药力f=1 230 J/g)，F为作动器滑动销运动所需克服的裕度阻力(滑动销1 ms运动到位，火药所需提供的最小推力)，S0为火药气体为滑动销提供驱动力的有效接触面积。由式(1)可知，火药的质量和滑动销运动所需克服的裕度阻力有明确的对应关系，因此，可以将过盈量与装药量的对应关系问题转化为过盈量和最小推力的对应关系问题。

3.2 过盈配合力学简化模型

首先，本文对过盈量与滑动销运动到位所需推力之间的关系进行理论分析。为了描述滑动销的运动状态，需对滑动销运动过程中所受阻力进行计算。为了计算的方便，我们这里只考虑滑动销两侧壁所受摩擦力。由于滑动销尺寸较小、材料刚度较大，配合时变形较小，因此可以将滑动销与基板接触面受力近似为均匀的平面接触力[11]。设p为过盈配合接触面的接触压力，δ为双边过盈量，S为接触面积，μ为摩擦系数，则过盈配合时摩擦力Ff为[12]：

Ff=p×S×μ

(2)

假设基板为刚体，将滑动销模型简化为左右两端面均匀受力的长方形单元体，则单元体的应力状态如图4所示。

摄影照片分为单独照片、组照及专题摄影等多种类型，新闻摄影人员经常会用到的发稿方式为单幅照片。为切实提升拍摄作品质量，有效体现出拍摄中摄影技巧及艺术手法，需在选择摄影照片时注重拍摄画面的和谐性，拍摄人物的动作及表情是否自然等要素，确保新闻摄影能够更好地反映出新闻事件的真实情况。

图4 单元体应力状态Fig.4 Element stress state

以水平轴为x轴，铅垂轴为y轴，建立坐标系，则该单元体应力状态为：

(3)

根据广义胡克定律可知：

(4)

式(4)中，E为弹性模量、v为泊松比。故单元在x、z方向上的变形为：

(5)

由式(4)和式(5)可得：

(6)

由上述关系式可知单元体的变形很小，即在过盈配合状态下滑动销与基板槽壁的接触面积增量可忽略不计。因此，可将式(6)直接代入式(2)中，则可得出摩擦力与过盈量之间的关系为：

(7)

由式(7)可知接触面积越大摩擦力越大，摩擦力与过盈量呈线性关系。由于滑动销运动过程中接触面积逐渐增大，因此，滑动销运动过程中摩擦力逐渐增大。假设滑动销运动到位所需最小推力为Fmin，滑动销运动位移为L，则由相关物理学和高等数学知识可得滑动销的运动学方程为：

(8)

对式(8)求解，可得微分方程通解为：

(9)

化简式(9)可得最小推力Fmin与过盈量δ的关系为：

(10)

由于作动器动作时间t非常短(毫秒级)，因此式(10)可进一步简化为：

(11)

式(11)中，c1为与作动器结构相关的常系数。

作动器工作时的实际力学环境要比简化模型复杂的多，对简化模型结果影响最大的是滑动销在x方向上的变形量Δlx。在简化模型中基板被视为刚体，无形变，因此，滑动销在x方向变形量Δlx即为双边过盈量δ。然而，在真实的工作过程中，基板为变形体，过盈配合作用下滑动销和基板会同时发生变形。因此，滑动销在x方向实际变形量Δlx小于双边过盈量δ。但是，滑动销x方向实际变形量Δlx与双边过盈量δ有关。若将滑动销x方向变形量Δlx表示为变量δ的函数[13]，则可对简化模型的分析结果进行修正。修正后最小推力Fmin为：

(12)

另一方面，过盈配合接触面的接触应力并非均布载荷，基板槽壁根部应力较大，接触面的接触应力沿z方向递减。利用传统的计算方法很难准确计算出滑动销运动位所需最小推力，因此，借助有限元仿真软件Ansys Workbench对作动器滑动销运动到位所需最小推力进行计算，以验证过盈配合力学简化模型的正确性。

3.3 作动器的有限元数值模拟

过盈问题是接触问题的一种，属于边界条件高度非线性的复杂问题[14]。由于作动器真实受力环境较为复杂，直接得到过盈量与最小推力之间的关系非常困难。因此，借助有限元仿真软件Ansys Workbench的瞬态分析模块对不同过盈量对应最小推力进行计算，并根据仿真结果建立过盈量与最小推力函数关系，以验证上述简化模型的合理性。

3.3.1有限元仿真模型的建立

通过有限元仿真软件Ansys Workbench的瞬态分析模块对作动器的受力情况进行求解，以得到作动器过盈量和最小推动力之间关系。首先，在Ansys Workbench瞬态分析模块中建立如图5所示的作动器有限元仿真模型。其次，为作动器赋予材料属性，作动器材料设置为结构钢。然后，定义作动器接触，如图6所示通过设置滑动销与基板侧壁接触面偏移量来模拟过盈配合。最后，定义作动器相关约束，如图7所示在滑动销上施加集中作用力。如图8所示为作动器的网格划分结果。

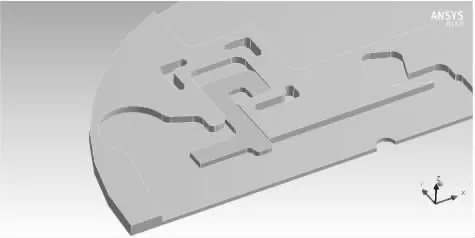
图5 作动器仿真模型Fig.5 Actuator simulation model

图6 作动器接触设置Fig.6 Actuator contact setting

图7 载荷施加位置Fig.7 Load position

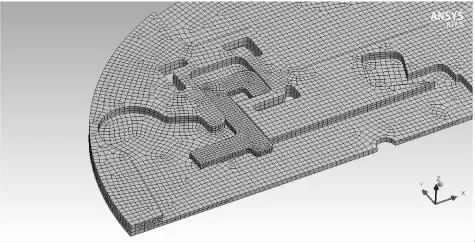
图8 作动器网格划分结果Fig.8 Grid division result of actuator

仿真过程中固定某一过盈量的值，通过改变推力大小求解相应最小推力。本文对不同过盈量的作动器所需最小推力进行了计算，即求解不同过盈量条件下使滑动销在1 ms内运动到位的最小作用力，以准确分析出过盈量与最小推力之间的函数关系。仿真求解时，集中力的大小取值间隔为10 N。

3.3.2仿真结果分析

图9为作动器过盈量δ=0.005 mm、推力F=250 N时不同时刻瞬态分析结果。由仿真结果可知250 N集中力可以使过盈量为0.005 mm的作动器滑动销在1 ms内运动到位。

图9 不同时刻作动器的应力分布云图Fig.9 Stress cloud map of actuator at different time

图10(a)所示为在推力F的作用下滑动销位移随时间的变化曲线，根据仿真结果可知起始阶段滑动销与基板接触面积较小，过盈配合面间的摩擦力较小，在推力F的作用下，滑动销的加速度值较大，滑动销处于加速阶段。随着滑动销与基板接触面积增大，过盈配合面间的摩擦力也增大，滑动销的加速度减小为零，滑动销处于匀速运动阶段。滑动销碰撞到基板时发生微弱反弹，最后静止且与基板接触。图10(b)为作动器在推力F的作用下作动器最大应力随时间变化曲线，根据仿真结果可知作动器滑动销启动瞬间应力较大，在滑动销运动过程中最大应力在一定范围内波动。

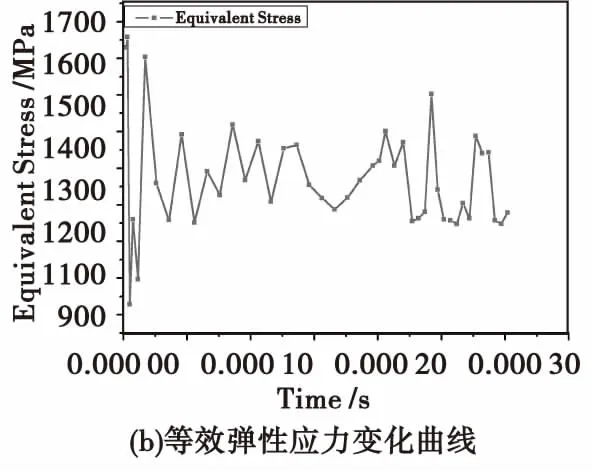
图10 滑动销位移及应力曲线Fig.10 Sliding pin displacement and equivalent stress curve

本文利用Ansys Workbench对不同过盈量下的最小推力进行了求解，如表1所示为仿真所得过盈量与最小推力之间的数值对应关系。根据仿真结果绘制了如图11所示折线图。

表1 不同过盈量对应最小推力数值的仿真结果Tab.1 Simulation results of minimum thrust values for different interference amounts

图11 过盈量与最小推力的关系曲线Fig.11 The curve of the relation between the interference and the minimum thrust

由于仿真时推力F取值间隔为10 N，所以求解的最小推力不一定是作动器在相应过盈量δ下最准确的最小推力，仿真结果存在10 N的误差。由上述仿真结果可得过盈量δ与最小推力F之间的关系式为：

F=kn·δ+Km=5 000δ-10

(13)

式(13)中，Km为修正系数。在过盈量δ与最小推力F之间的关系式中，修系数Km的数值远小于比例系数kn，因此可Km忽略不计。对比式(13)和式(12)可知Y(δ)为关于δ的一次函数[16]。设Y(δ)=n%×δ，则可将式(13)进一步修正为：

(14)

式(14)中，n%×δ为滑动销在x方向上的变形量。引入修正系数Km，则可得作动器过盈量δ与最小推力Fmin关系式为：

(15)

由构建的过盈配合力学简化模型和有限元仿真结果可知，过盈量δ与最小推力F之间呈明显的线性关系。仿真结果与简化模型的分析结果一致，即验证了简化模型的合理性。结合式(15)和式(1)可得过盈量与装药量之间关系为：

(16)

虽然，有限元仿真方法能够较准确的模拟作动器的力学状态，但是，滑动销与基板之间的过盈配合状态受过盈配合接触面粗糙度、配合长度、摩擦系数、外部载荷等参数的影响[15-17]。因此，火药作动器的应用需要大量实验验证。

4 结论

本文提出了滑动销与基板过盈配合的微小型火药作动器。该作动器采用过盈配合的方式将可动部件滑动销与作动器基板装配一起，简化了传统火药作动器结构，促进了微小型火药作动器的小型化。数值仿真结果表明过盈量δ与最小推力F之间呈明显的线性关系，数值仿真结果与简化模型理论分析结论一致。然而，滑动销与基板之间的过盈配合状态会随着多种环境条件的变化而变化，因此，还需大量实验验证，以促进火药作动器的工程化应用。本文上述理论结果为作动器设计提供了理论支撑。