强度及裂缝双控条件下钢筋混凝土板截面优化设计探讨
2018-08-20周维祥
周维祥
(上海市政工程设计研究总院(集团)有限公司 200092)
引言
在混凝土结构截面设计时,混凝土板配筋除需要承载力验算外,还要满足正常使用状态条件下裂缝控制要求,但现有国内外钢筋混凝土构件截面优化研究都集中在强度控制条件下采用解析法[1-3]、遗传算法[4]计算单筋最优板厚或最优配筋率上,忽略了裂缝限值条件,而在给水排水混凝土结构截面设计过程中,必须要进行裂缝验算,并且往往也对配筋起控制作用,所以承载力控制条件下的“最优板厚”并不是真正的最优板厚。另外,混凝土板中往往有两层及以上受力钢筋承受面外弯矩,因此十分有必要进行承载力及裂缝双控条件下多层钢筋受力的最优板厚及最优配筋率研究。本文通过引入钢筋混凝土构件受弯承载力计算及裂缝验算公式,在满足结构安全和裂缝限值的条件下,对单位面积钢筋混凝土板造价目标函数求导得到理论最小值,进而得到特定弯矩值所需要的最优板厚及对应配筋率。
1 造价目标函数
假设单位面积钢筋混凝土板造价为C。板厚度为h=h0+as,双层双向配筋,各钢筋层配筋率分别为钢筋综合单价为Cs(元/m3),混凝土综合单价为Cc(元/t),钢筋容重为ρs(t/m3),则:
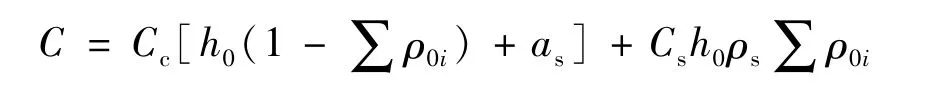
考虑到Cs、Cc、ρs都为常数,在保护层厚度C一定的情况下,as变化幅度很小。令mc=最终定义造价目标函数为:

2 约束条件
规范[5,6]及手册[7]规定,结构设计要满足强度、刚度、裂缝以及构造等要求。而设计过程中强度计算、裂缝验算是最基本的、最主要的,通常对截面设计及结构造价起控制作用。
2.1 强度条件
单筋纯弯构件截面达到极限破坏时,极限弯矩为:

联立式(2)和式(3)得到:

2.2 裂缝条件
根据GB 50069-2002规范[6]附录A,裂缝验算公式为:
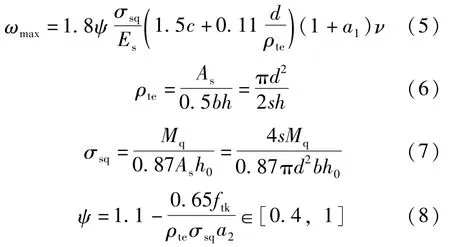
其中,纯弯构件时,取a1=0,a2=1。令:

将式(7)、式(8)代入式(5),可简化得到钢筋直径d的一元三次方程:
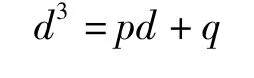
根据卡尔丹求根公式:
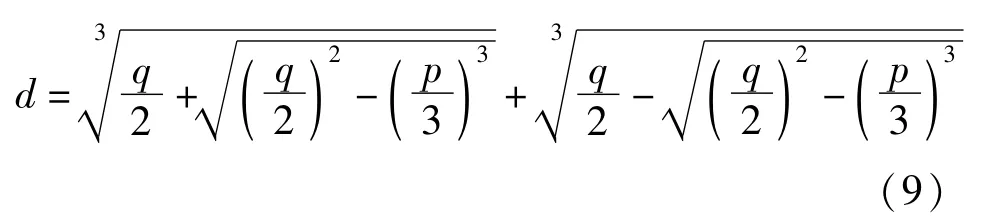
对应满足裂缝限值的配筋率:

3 截面设计优化
3.1 强度条件下单筋截面设计优化
单层受力钢筋在强度控制条件下的最优板厚可通过解析方法得到。其中非受力的三层钢筋按有效截面的最小配筋率配置。
将式(4)代入式(1),并对强度控制条件下的造价目标函数求导:
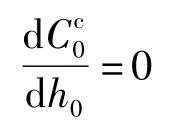
则最优有效截面高度:

最优配筋率:
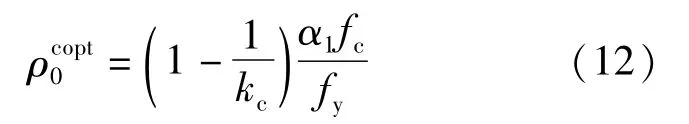
3.2 双控条件下多层受力钢筋的截面设计优化思路
当考虑多层受力钢筋时,强度控制条件的最优板厚很难通过解析法得出,而考虑到裂缝控制函数的不连续性,双控条件下多层受力钢筋的最优板厚采用数值解法是个不错的选择。
数值解法通过设定壁厚有效高度的搜索区间和特定步长,在一定设计参数条件下,通过极值算法得到造价函数的最小值,对应板厚即为最优板厚。
本节以常用设计参数(表1)为例对造价目标函数进行优化。其中采用细而密的配筋可以更好地满足裂缝要求,但间距s不宜小于100mm[6],故假设钢筋中心间距s=100mm。
3.3 截面有效高度范围
在确定的受力钢筋对应弯矩值组合作用下,考虑最大配筋率和最小配筋率限制,对应强度控制条件及裂缝控制条件都有最小壁厚和最大壁厚,并且都由弯矩组合中的最大弯矩值控制。有效高度范围的确定方法见图1。
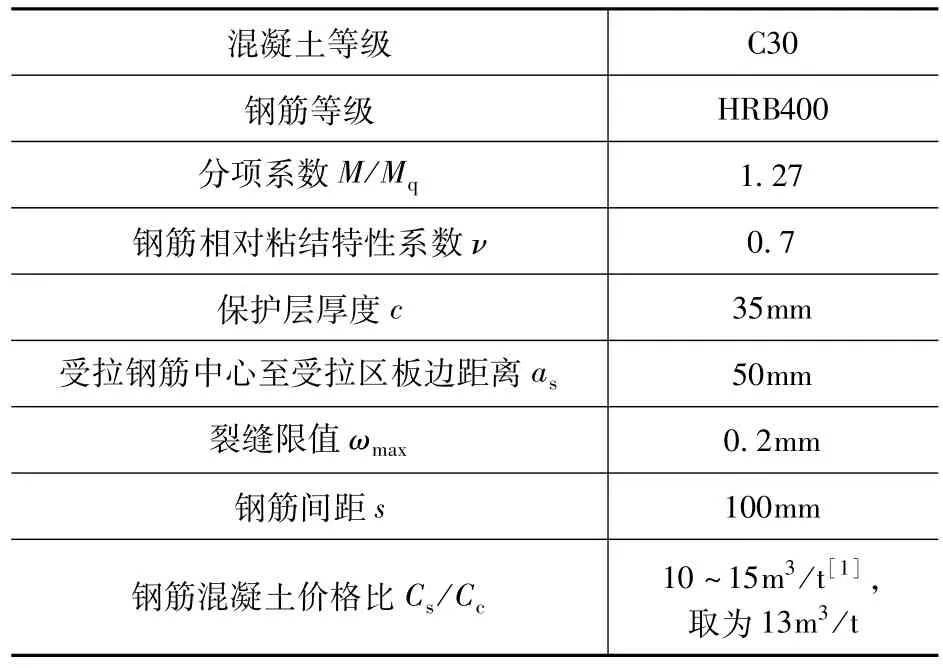
表1 设计参数Tab.1 Design parameter

图1 有效高度范围示意Fig.1 Effective height range
最小配筋率验算时,取全截面配筋率:
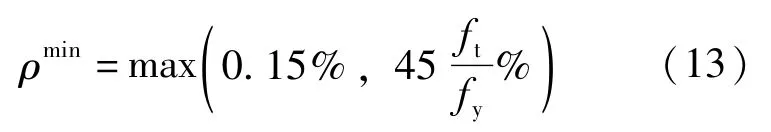
当达到最大受压区高度时,

对应强度控制条件下:

对应裂缝条件时,解析方法得到最大、最小有效高度比较困难,但可以通过数值方法得出,分别记而最终最优有效高度范围如下:
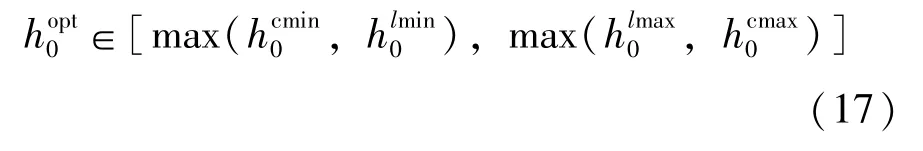
3.4 造价目标函数形态
将式(4)和式(10)分别代入式(1)后可得到强度控制造价目标函数(不考虑受压区钢筋)、裂缝控制造价目标函数与有效截面高度的关系。不同的弯矩值组合的造价目标函数呈现出不同的形式。为方便研究,本节假定控制弯矩相等,并取25kN·m、100kN·m、500kN·m三档,按控制弯矩的数量不同分别研究。
图2中只有一个方向控制弯矩,其余三层钢筋都按最小配筋率考虑。强度控制造价目标函数随着板厚的增加先少后多,而裂缝控制造价目标函数随着板厚的增加逐渐增加。图中黑色点划线对应横坐标为最优板厚的有效截面高度(下同)。当弯矩较小时,双控条件的造价最低值即强度条件的最低值;而弯矩增大时,最优板厚由两个函数的交点确定;而当弯矩大于一定数值时,最优板厚为最小壁厚,对应配筋率为最大配筋率。
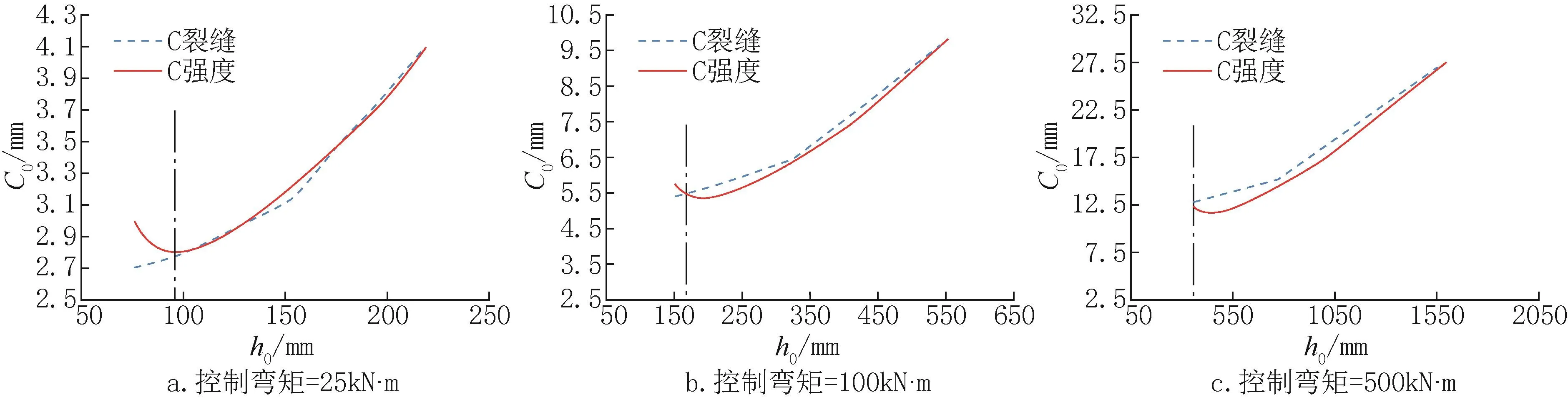
图2 Mq1控制时C0-h0曲线Fig.2 C0-h0curve for Mq1control only
图3 ~图5中分别有2~4个相等的控制弯矩,其余钢筋层按最小配筋率考虑。两个造价目标函数都随着板厚的增加先减小后增大。特别的,裂缝控制函数的拐点对应式(8)ψ=0.4,此时:
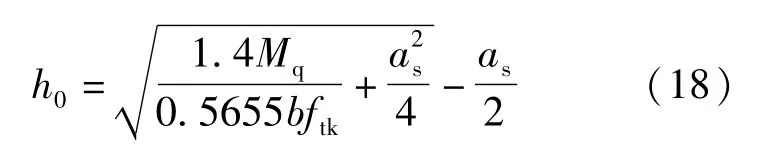
当弯矩较小时,最优板厚由两个函数的交点确定,随着控制弯矩数量增加,最优板厚随之增大;而弯矩较大时,裂缝条件控制配筋,最优板厚对应裂缝控制造价函数拐点,式(18)所列表达式即为最优有效高度。

图3 Mq1=Mq2控制时C0-h0曲线Fig.3 C0-h0curve for Mq1=Mq2control only

图4 Mq1=Mq2=Mq3控制时C0-h0曲线Fig.4 C0-h0curve for Mq1=Mq2=Mq3control only

图5 Mq1=Mq2=Mq3=Mq4控制时C0-h0曲线Fig.5 C0-h0curve for Mq1=Mq2=Mq3=Mq4control
3.5 最优板厚有效高度和配筋率
通过最小值搜索,可以根据图2~图5方便地得到最优板厚h0,进而通过式(4)和式(10)得到最优配筋率
图6中双向、三向、四向相同弯矩控制条件下最优板厚曲线除小弯矩情况外完全重合,且约等于单向控制弯矩条件下最优板厚的2倍。在允许一定误差并考虑实际壁厚模数(50mm)的条件下,可以近似以式(16)作为单向配筋的最优板厚,以式(18)作为双向以上配筋的最优板厚。显然近似与成正比。

图6 -Mq曲线Fig.6 -Mqcurve
图7中双向、三向、四向相同弯矩控制条件下经济配筋率除小弯矩情况外完全重合,都分布在0.35%~0.45%之间,且随着控制弯矩的增大逐渐增大。而单向控制弯矩条件下经济配筋率分布在1.1%~2.05%之间,其中当弯矩大于400kN·m时,经济配筋率即最大配筋率。
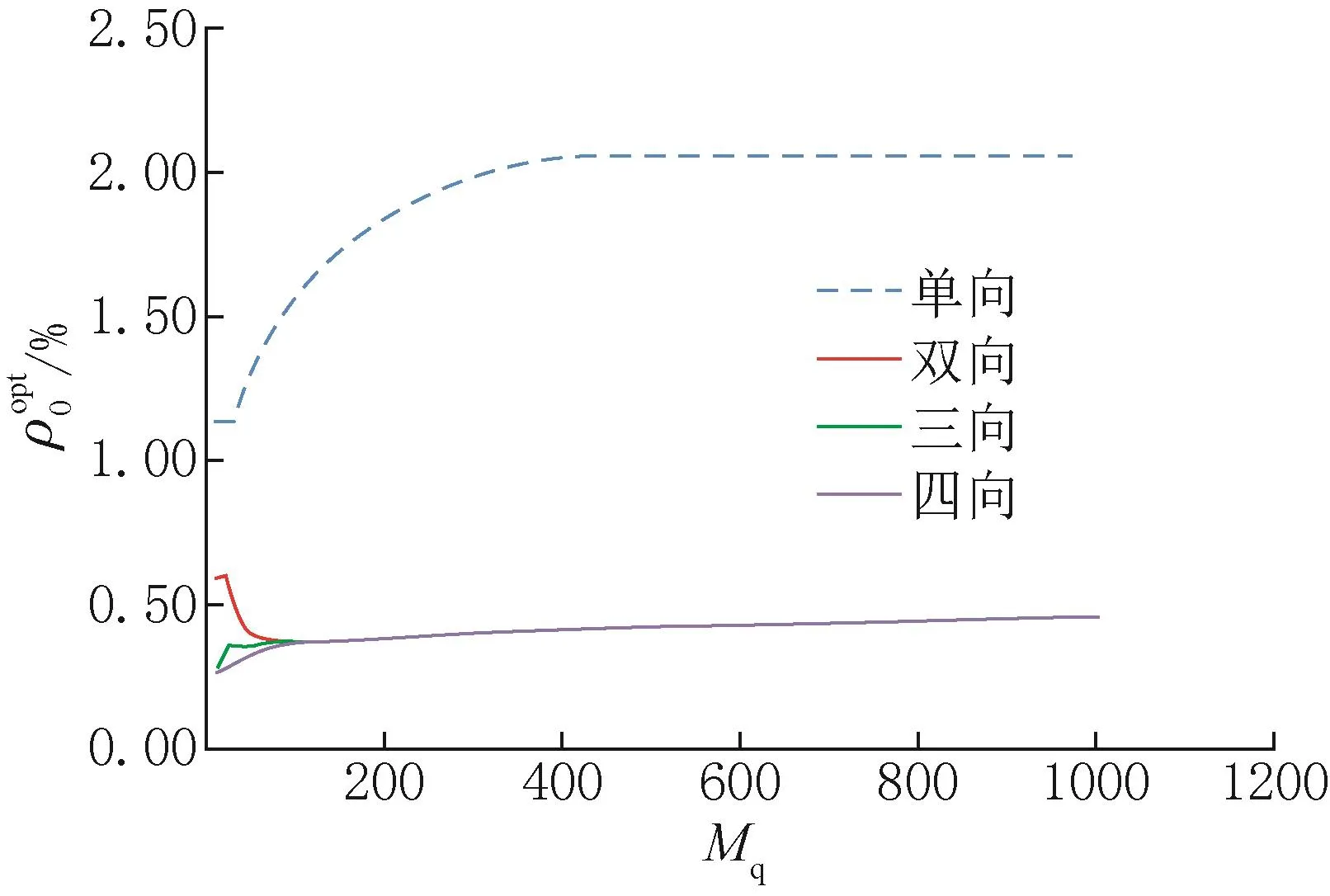
图7 -Mq曲线Fig.7 -Mqcurve
图8 为单向弯矩控制条件下不同Cs/Cc时的曲线。结果表明,在有限的钢筋混凝土价格比变动下,最优板厚并不明显变化。因此,在截面设计时可不考虑价格的因素。

图8 不同Cs/Cc条件下-Mq曲线Fig.8 -Mqcurve for different Cs/Cc
4 算例
4.1 算例一
悬臂单向板,内水工况,水深5.2m。钢筋、混凝土综合单价同文献[4]中算例。计算见表2,造价随着有效高度的增加而增加,最优板厚有效高度为最小有效高度239mm,此时可按50mm模数取板厚h=h0+as=250+50=300mm,配筋率为1.76%。
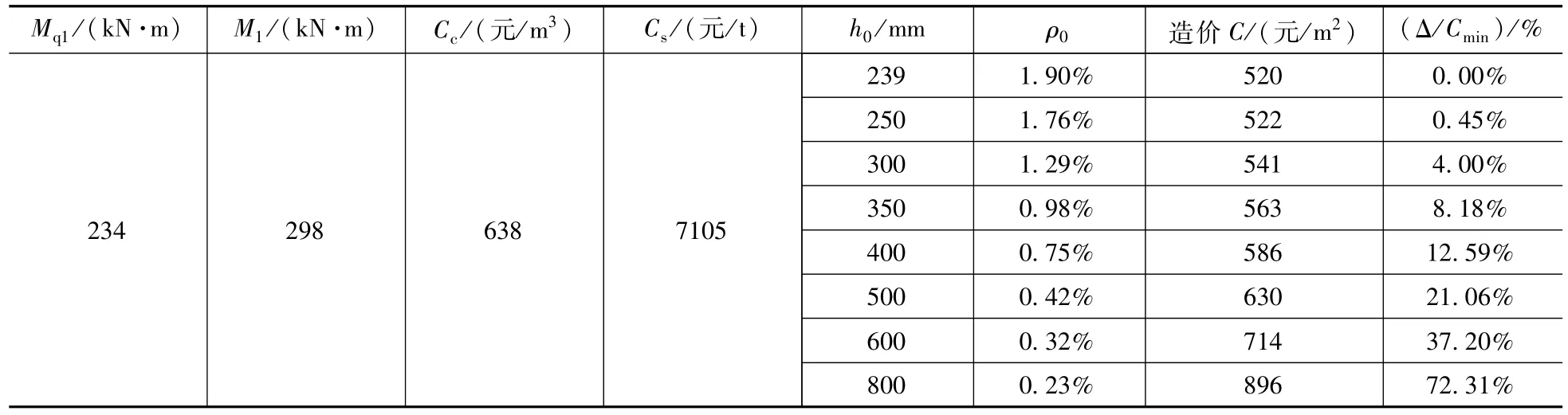
表2 算例一Tab.2 Calculate example 1
4.2 算例二
悬臂单向板,内水+外水土工况,两侧弯矩相同,其余同算例一。计算见表3,造价随着有效高度的增加先降低、后增加,最优板厚有效高度为512mm,此时可取板厚为500+50=550mm,配筋率为0.42%。
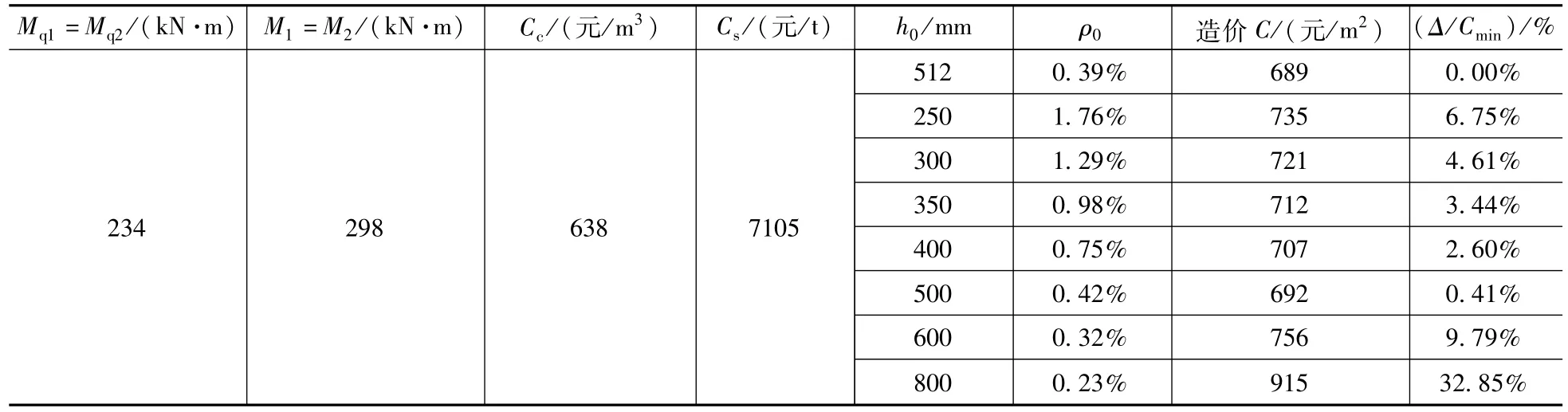
表3 算例二Tab.3 Calculate example 2
5 结语
本文通过构造造价目标函数,引入强度控制条件及裂缝控制条件,经过理论推导和图表分析,得到了不同弯矩组合作用下纯弯板的最优板厚高度及对应配筋率,并得出以下通用性的认识:
1.本文通过理论推导,得到了裂缝控制配筋关于板厚和弯矩的显式表达,即As=f(h,Mq)。可以摒弃以往的试算方法,而直接通过公式求得裂缝配筋。
3.单向控制弯矩条件下经济配筋率分布在1.1%~2.05%之间,其中当弯矩大于400kN·m时,经济配筋率即最大配筋率。
4.双向及以上相同弯矩控制条件下经济配筋率除小弯矩情况外完全重合,都分布在0.35%~0.45%之间。
5.在有限的钢筋混凝土价格比变动下,最优板厚变化不明显。
6.实际工程中,经常碰到变截面、分离式配筋等情况,还需要考虑轴力、抗剪、挠度等要求。因此本文仅对纯弯板的优化设计进行理论探讨,实际板厚还需要综合施工质量、抗渗等因素来确定。
