节点半刚性对K6单层木网壳稳定性能的影响

2018-08-20何敏娟胡超舒展

特种结构 2018年4期

何敏娟胡超舒展

（同济大学建筑工程系上海200092）

引言

近年来国内外空间结构迅速发展，其建筑外观新颖且形式种类繁多［1］。木空间结构建造技术在我国也逐渐兴起，而单层木网壳结构作为木结构和空间结构相结合的产物而逐渐受到关注。有关单层木网壳的研究成果，多聚焦于木网壳节点受力性能研究以及木网壳稳定性能研究等方面。孙小鸾等［2］对木网壳结构半刚性装配式植筋节点受力性能进行试验研究，并引入相关性能系数对幂函数拟合模型进行改进，最终获得节点的半刚性抗弯刚度模型。罗伟等［3］为研究节点半刚性对木网壳整体稳定性能的影响，设计半刚性节点并将其用于单层球面木网壳缩尺模型中，并对该模型进行加载试验，试验结果表明半刚性节点木网壳具有稳定承载能力。周金将等［4］对单层木网壳半刚性节点进行刚度试验研究，发现节点刚度对网壳整体稳定性影响较为显著，可通过设计优化使半刚性节点满足单层网壳稳定性设计要求。何敏娟等［5］对木空间结构的研究现状及关键问题进行详细综述，表明木空间结构具有非常广阔的研究前景。

网壳结构的稳定性是网壳结构分析设计中的一个关键问题［6］。网壳结构多发生失稳破坏，而非超越承载能力极限状态发生破坏［7-9］。我国《空间结构网格技术规程》中第3.1.8条指出：“单层网壳应采用刚接节点”。但多数装配化节点的转动刚度介于刚接节点与铰接节点之间，无法满足规程所建议的刚接节点设计要求。为此有关学者［10-13］通过研究节点半刚性对网壳稳定性能的影响，得出半刚性节点网壳结构也可能具有良好的承载能力及稳定性能等结论。上述结论为半刚性节点在木空间结构中的推广应用提供了诸多可能。

节点半刚性概念主要是基于节点刚度而提出的，但如何界定某种节点是否为半刚性节点还没有统一定论。曾有学者通过节点弯矩-转角曲线来定义螺栓连接等节点的抗弯性能，如Swanson等［14］根据钢结构螺栓节点在受到弯矩作用时获得的性能曲线，将节点从承载力、延性及刚度三个指标进行分类评价。就承载力而言，依据节点是否可完全传递框架梁端的塑性弯矩，分为全强度（记为FS）和部分强度（记为PS）；就延性而言，依据节点可达到并维持一定塑性转角需求能力的不同，分为脆性和延性；就刚度而言，依据节点抗弯刚度的不同，分为刚接特性（记为FR）、部分刚接特性（记为PR）以及铰接特性（记为Pinned），如图1所示。其中部分刚接特性即为节点抗弯时所表现出的半刚性特征。

图1 钢结构螺栓节点弯矩-转角曲线［14］Fig.1 Typical moment-rotation curve of bolted steel connection［14］

本文拟设计一种新型填板式木网壳节点，来探究节点与木杆件在装配时所形成的轴线间夹角值对木网壳节点抗弯性能的影响。节点抗弯性能试验采用弯矩与轴向压力联合作用形式。通过试验获得不同类型木网壳节点的弯矩-转角关系曲线，再结合数值模拟方法分析节点的抗弯工作机理，并提出设计中可供借鉴的四折线抗弯刚度模型。随后利用ANSYS有限元软件建立考虑节点转动刚度影响的精细化木网壳整体数值模型，采用COMBIN39非线性弹簧单元考虑节点半刚性影响。最后对该数值模型进行参数分析，来评估节点半刚性对K6单层木网壳稳定性能的影响。

1 填板式木网壳节点受力性能研究

1.1 木网壳节点概念设计

对节点转动刚度的研究是分析和设计半刚性节点网壳结构的首要一步［15］。木网壳节点概念设计需要综合考虑结构、杆件以及节点等多个层面。例如结构层面上需要综合考虑网壳结构设计原则，从而确定网壳形式及网壳选型；杆件层面上则需要综合考虑网壳跨度、矢跨比以及网格形式等因素的影响；节点设计则需要考虑综合结构及杆件等层面进行合理设计。选择跨度偏中小型、网格形式为扇形三向网格型、杆件截面尺寸为150mm×200mm、节点类型为填板式节点的木网壳结构作为研究对象。

1.2 木网壳节点试件设计

在已有节点抗弯试验中，节点两侧所连杆件轴线与节点中心轴线往往呈直角关系，节点整体呈水平状态承受竖向荷载作用。对比国内外不同木网壳工程实例，可以看出当网壳跨度较大且构件尺寸偏大的情况下，杆件轴线多呈现曲线形态。该设计理念旨在消除杆件与节点在装配过程中不可避免的“轴线间夹角值”影响，以保证构件轴线形态能够最佳地适应网壳曲面形态。但该设计对杆件轴线形态在加工精度上要求较高，否则会出现装配不良等情况。

相比于跨度较大的网壳结构来说，中小型跨度网壳具有网壳规格不大且杆件尺寸适中等特点。木杆件亦无需加工成曲线型轴线形态，可按照直线型轴线形态进行预制加工。不过这一设计理念所引发的思考却是轴线间夹角值在节点与杆件装配上所带来的影响。

为研究轴线间夹角值对节点抗弯性能的影响，在设计节点试件时通常需要对轴线间夹角值进行相应调整。通过对不同跨度、不同矢跨比条件下的木网壳几何模型进行轴线间夹角值统计，其规律如下：当网壳跨度不变时，轴线间夹角值呈离散性分布，而其统计值（如平均值）与网壳矢跨比数值表现出正相关关系。根据压弯联合作用下节点抗弯性能试验的设计思路，综合考虑木网壳结构形式以及轴线间夹角值等设计因素的影响，选择跨度为30m、矢跨比为1/3的网壳几何模型进行统计。最终将“轴线间夹角值”范围控制在4°～8°之间，并选择两端的边界值作为节点试验的设计变量。有关轴线间夹角值的几何示意如图2所示。

图2 轴线间夹角值Fig.2 Angle value between two axes

木网壳节点采用高度适合装配化的填板式节点形式，其概念设计如图3所示。该节点主要是由中心钢连接器（含外伸钢填板）以及周围胶合木杆件通过螺栓连接而成。外伸钢填板嵌入预先开好槽的木杆件内，再通过螺栓群将节点和杆件连接起来。

图3 木网壳节点概念设计Fig.3 Conceptual design of timber shell joint

如图4所示为木网壳节点试验各组件间装配关系示意，中心钢连接器根据力学等效原理进行相应简化；边界约束装置保证木杆件端部在平面内转动的同时还可承受结构超静定作用带来的轴向压力；再将边界约束装置与试验机支座可靠连接。在构件材料选择上，木杆件采用SPF2级胶合木材，钢构件采用Q235号钢材。

图4 木网壳节点试验各组件Fig.4 Components of timber shell joint test

1.3 木网壳节点抗弯性能试验研究

如图5所示为节点试验设计简图及现场加载图。节点试验加载装置采用邦威JAW-500F型多功能结构试验系统进行单调加载试验，并采用位移计和采集箱获取木网壳节点在抗弯过程中所需测量部位的位移值。加载速率主要参考ASTMD1761-88［16］试验标准取（3 ～5）mm/min，节点抗弯试验中取4mm/min。

依据轴线间夹角值的不同，木网壳节点总共设计为两大类，试件编号分别为J4型、J8型。字母部分J代表节点，数字部分代表轴线间夹角值4°或8°。每类木网壳节点设计三组试件，共计六组。J4型与J8型木网壳节点在加载过程中杆件裂缝发展及螺栓变形情况如图6所示。

图6 木网壳节点杆件裂缝发展及螺栓变形情况Fig.6 Crack development and bolt deformation of joints

试验现象表明，两类节点在压弯联合作用下具有类似破坏特征：一是从木螺栓孔壁出发，沿木纹方向出现的脆性断裂；二是木螺栓孔孔壁与螺杆在接触过程中出现的孔壁承压破坏；三是螺杆在传递内力过程中出现所谓的一点屈服破坏，导致试验加载后部分螺杆出现轻微弯曲。

有关J4型与J8型节点在压弯联合作用条件下的弯矩-转角试验曲线如图7所示。其中纵轴表示节点域所受弯矩值，横轴表示节点域转动的角度。试验结果表明：轴线间夹角值不同的木网壳节点，对应的弯矩-转角关系试验曲线形态也有所不同。从这一点可以初步揭示木网壳节点的抗弯性能在一定程度上会受到轴线间夹角值的影响。

两类节点对应抗弯性能试验曲线具有以下特点：首先，两类节点维持初始抗弯刚度的历程有所不同；其次，木杆件在发生脆性断裂之前，两类节点的抗弯性能有所不同：J4型节点在维持一定初始刚度后，表现为转角不断增大而抗弯承载力水平保持不变的低水平刚度状态，后期随着节点各部件建立稳定接触关系，抗弯刚度值稳定变化，直至节点破坏；而J8型节点初始刚度维持历程较长，后期抗弯刚度虽有所下降，但很快进入稳步增长状态，节点低水平刚度段没有J4型节点显著，之后抗弯刚度逐渐增加，直至节点发生破坏。总体来讲，前期初始抗弯刚度及低水平刚度段上表现有所差异，其他阶段抗弯性能较为相似。

图7 木网壳节点弯矩-转角关系M-θ试验曲线Fig.7 Experimental M-θ curves of timber shell joints

1.4 木网壳节点抗弯性能数值模拟研究

数值模拟方法能够很好地弥补试验条件所带来的局限。合理运用数值模拟方法可以获取在现有试验条件下较难获取到的数值计算结果，继而可进一步探究木网壳节点在轴弯联合作用下的抗弯工作机理。

如图8所示为两类木网壳节点在数值模拟条件下的未受荷状态和受荷状态。当位移荷载逐步施加后，节点整体产生向下位移，伴随着中心钢连接器两侧的节点域产生转动趋势。

有关木网壳节点的弯矩-转角关系（M-θ）试验曲线与数值模拟曲线如图9所示。建模时将木材简化为正交各向异性弹塑性材料，各部件间接触参数与螺栓荷载值参考文献［17］中相关建议数值，最终获得数值模拟条件下木网壳节点的弯矩-转角曲线。

利用ABAQUS有限元软件对木网壳节点进行精细化建模，可得到节点在数值模拟条件下的弯矩-转角关系曲线，再通过软件后处理模块分析节点抗弯过程，发现木网壳节点在压弯联合作用条件下大致可分为四个工作阶段：

图8 数值模拟条件下木网壳节点装配状态与受弯状态Fig.8 Assembly and load-bearing states of timber shell joints by numerical simulation

图9 木网壳节点弯矩转角关系M-θ试验与数值模拟曲线Fig.9 Experimental and numerical M-θ curves

第一，螺栓嵌固阶段，具体特征为外伸填板未与螺栓杆建立接触，此时外伸填板端面与木槽底部相互挤压，外伸填板表面与木槽表面发生挤压摩擦等作用来产生抗弯刚度；

第二，螺栓滑移阶段，具体特征为外伸填板进一步发生向下位移，导致填板螺栓孔壁与施加预紧力的螺栓杆表面发生接触，继而推动螺栓产生微小位移，并逐步使螺栓杆表面与木材螺栓孔壁建立接触；

第三，孔壁承压阶段，具体特征为螺栓杆表面与木材螺栓孔壁建立紧密接触，抗弯承载力主要通过接触力绕转动中心所形成的内力矩来提供。此阶段接触区域应力较为集中，脆性裂纹由此萌生；

第四，节点失效阶段，具体特征为胶合木杆件发生沿轴线方向且穿过螺栓孔壁的脆性断裂。节点抗弯承载力虽然出现较大幅度下降，虽然残余强度仍然存在，但此时应视为节点已退出工作。

根据上述不同阶段的性能表现，拟采用四折线刚度模型来近似表征节点在轴弯联合作用下的抗弯刚度变化，具体见图10。其中，Kf为螺栓嵌固阶段的抗弯刚度、Mf为螺栓滑移段分界弯矩值、θf为螺栓滑移段分界转角值；Ks为螺栓滑移阶段的抗弯刚度、Ms为孔壁承压段分界弯矩值、θs为孔壁承压段分界转角值；Ku为孔壁承压阶段的抗弯刚度、Mu为极限弯矩值；θu为极限转角值。

图10 四折线刚度模型Fig.10 Four-linear rigidity model

该节点刚度模型主要由性能点和性能段构成，性能段可大致上将节点抗弯全过程简化为四阶段线性抗弯性能段，而性能段间的分界点则作为节点抗弯刚度模型的性能点。本文主要结合数值模拟结果探求刚度模型性能段分布，并结合节点试验数据获得刚度模型性能点。最终采用四折线刚度模型来近似评价J4型节点和J8型节点的抗弯性能。有关不同类型节点对应的四折线刚度模型及性能点参数如图11及表1所示。

图11 木网壳节点四折线刚度模型Fig.11 Four-line rigidity model according to test data

表1 木网壳节点抗弯刚度模型性能点参数Tab.1 The performance points of joint rigidity models from test data

1.5 木网壳节点抗弯性能研究结论

通过试验研究以及数值模拟方法对新型填板式木网壳节点受力性能进行分析，发现节点抗弯刚度介于铰接节点和刚接节点之间，具有典型的半刚性特征。

2 单层木网壳数值模型介绍

木网壳整体数值模型采用ANSYS通用有限元软件建立而成。如图12所示为木网壳杆件及半刚性节点单元类型。考虑到所设计填板式木网壳节点在节点连接区域的材性属性从钢材过渡至木材，因而在建模时将杆件进行分段处理，连接方式为“钢连接器段-半刚性节点-胶合木杆件段”。

具体连接方式如下：

以A、B节点作为填板式木网壳节点中心所在位置，钢连接器沿主节点连线方向延伸至1、4位置，延伸长度近似取为主节点到节点域转动中心间的距离L1，而胶合木杆件单元则通过连接节点2及节点3来建立，长度为L0。考虑到非线性弹簧单元在建模时可忽略其单元长度，因此将1、2与3、4设置为重合节点，并通过COMBIN39非线性弹簧单元连接重合节点来引入半刚性节点。

图12 木网壳杆件及节点单元类型Fig.12 Element type of timber member and semi-rigid joint

关于木网壳整体有限元模型的加载方式，主要按照静力等效原理，将节点附近区域内的荷载集中作用于主节点上。先依据主节点及杆件位置建立多边形网格面，并将其定义为SURF154表面效应单元，对所有主节点施加约束，并在多边形网格面上施加均布面荷载，通过ANSYS求解到所有主节点处的支承反力。将支承反力的反向荷载作为等效节点荷载并记录于宏文件中。在未创建表面效应单元的原始模型上，调用等效节点荷载宏文件，便可完成等效节点荷载的施加。

考虑到节点抗弯试验选取的轴线间夹角值有限，节点轴线间夹角值呈离散状态分布，因此通过定义非线性弹簧单元实常数将四折线刚度模型性能点数值引入到有限元模型时需对不同位置处节点的轴线间夹角值进行分类。

为了探究节点半刚性对K6单层木网壳稳定性能的影响，基于该网壳数值模型进行参数分析。利用ADPL参数化建模方法建立大量网壳数值模型，计算半刚性节点木网壳在双非线性影响下其整体稳定承载力变化，并与刚接节点网壳进行对比。模型中钢构件部分均采用Q235号钢材的材料性能参数；胶合木本质上属于各向异性材料，鉴于没有成熟的理论可以精确定义其材料属性，因此在数值模拟中将其假定为均值连续且纹理平整的正交各向异性弹塑性材料。利用材性试验获得相关力学性能指标，再结合力学理论计算公式获得节点试验所用胶合木材的弹性及塑性参数，再将其赋予到网壳数值模型中。

具体参数分析方案如下：

（1）跨度及矢跨比。其中网壳跨度（L）有30m、40m等两类情况，网壳矢跨比（f/L）有1/3、1/4、1/5、1/6及1/7等五类情况。根据上述参数组合，并综合考虑分频数对杆件长度的影响，将分频数统一设置为6；

（2）节点抗弯刚度模型。为深入研究节点刚度模型对木网壳稳定承载力的影响，考虑包括基于木网壳节点四折线刚度模型的初始弹性刚度模型（OAEF曲线，简记为T-E）、初始非线性刚度模型（OAECD曲线，简记T-NE）、割线弹性刚度模型（OCG曲线，简记为S-E）、割线非线性刚度模型（OCD曲线，简记为S-NE）、四折线刚度模型（OABCD曲线）以及刚接模型，共6种情况。有关不同刚度模型的弯矩-转角曲线形态如图13所示；

图13 各刚度模型弯矩-转角曲线Fig.13 Moment-rotation curves of joint rigidity model

（3）几何初始缺陷。根据“一致缺陷模态法”，用最低阶屈曲模态来模拟木网壳结构的初始缺陷分布，最大幅值分别取0、L/3000、L/1500、L/1000、L/500以及L/300；

（4）荷载分布模式。主要考虑两种荷载分布形式，即满跨均布恒荷载g以及半跨均布活荷载p。活荷载p与恒荷载g比值分别取0、1/4、1/2及1；

（5）周边支承条件。网壳结构只在最外环节点上设置边界约束，主要分为两种支承方式：三向铰接和三向固接。

根据上述参数分析方案，共建立上百组木网壳有限元模型。如图14所示为跨度为40m、矢跨比为1/5、径向分频数为6且三向刚接的木网壳数值模型。

图14 木网壳结构整体数值模型Fig.14 FE model of timber shell structure

3 参数分析结果

为探究半刚性节点木网壳结构在不同设计参数影响下整体稳定承载力变化情况，利用数值模拟计算时均以对应刚接节点木网壳稳定承载力作对比，以定量评价节点半刚性影响。

3.1 跨度及矢跨比影响

有关跨度L与矢跨比f/L对半刚性节点木网壳整体稳定承载力的具体影响如图15及表2所示。图中纵坐标表示网壳整体稳定承载力，横坐标表示网壳矢跨比。表2中Pr表示刚接节点木网壳整体稳定承载力，Psr表示半刚性节点木网壳整体稳定承载力。由图15及表2可以看出，随着矢跨比数值逐渐增大，Pr与Psr总体呈现上升趋势（以下涉及到Pr与Psr的部分所代表的物理意义同上）。同样跨度下，Psr始终小于Pr，表明传统刚接节点建模计算出的网壳稳定承载力偏高，并且节点半刚性对稳定承载力的削弱作用大致上与矢跨比数值呈负相关关系。

图15 跨度及矢跨比影响Fig.15 The impact of span and height-to-span ratio

表2 跨度及矢跨比影响下木网壳整体稳定承载力（单位：kN/m2）Tab.2 Global buckling capacity of K6 reticulated timber shell influenced by span and height-to-span ratio（unit：kN/m2）

3.2 节点转动刚度模型影响

本文主要利用该弹簧单元引入6种不同形式的节点刚度模型，分别为初始弹性刚度、初始非线性刚度、割线弹性刚度、割线非线性刚度、四折线刚度以及刚接节点模型（图13）。为探究节点刚度模型对木网壳稳定性能的具体影响，本文仅以跨度30m及40m、矢跨比为1/5条件下的木网壳为研究对象进行讨论。表3给出了引入不同节点刚度模型后木网壳稳定承载力的变化情况。

从表3中可以看出，木网壳稳定承载力受节点转动刚度模型的影响较大。值得注意的是，当节点刚度模型对应的初始刚度值相近时，采用弹性刚度模型与非线性刚度模型进行计算所获得的网壳稳定承载力数值相差不大。通过横向对比可以看出不同的节点刚度模型，计算出的网壳稳定承载力也有所不同，并且呈现出一定规律。选用不同类型刚度模型计算出的木网壳稳定承载力从大到小排列，依次是：刚接模型＞初始刚度模型＞割线刚度模型；选用同种类型刚度模型计算出的木网壳稳定承载力从大到小排列，依次是：初始弹性刚度模型＞初始非线性刚度模型、割线弹性模型＞割线非线性刚度模型。

由此可见，选择不同的节点刚度模型会直接影响到半刚性节点初始刚度值的大小，或者说直接影响到节点在达到失效阶段前的抗弯刚度发展历程，导致引入不同节点刚度模型性能点参数后计算出的稳定承载力值也会有所不同。

表3 节点刚度模型影响下木网壳整体稳定承载力（单位：kN/m2）Tab.3 Global buckling capacity of K6 reticulated timber shell influenced by joint rigidity model（unit：kN/m2）

3.3 几何初始缺陷影响

有关几何初始缺陷值对半刚性节点木网壳稳定性的具体影响如图16及表4所示。本文仅以跨度30m及40m、矢跨比为1/5条件下的木网壳结构为研究对象进行讨论。

由图16及表4结果可以看出，按照一致缺陷模态法将特征值屈曲分析中得到的一阶屈曲模态引入到有限元模型中，致使半刚性节点网壳与刚接节点网壳稳定承载力均有所下降。随着初始缺陷值发生变化，节点半刚性对木网壳稳定承载力的削弱作用会在一定程度上受到几何初始缺陷的影响。整体上看，随着初始缺陷幅值的增大，节点半刚性对木网壳整体稳定承载力的削弱作用变得更加显著。究其原因，主要是因为初始缺陷值的不同会导致网壳初始几何形态发生不同程度的改变。当初始缺陷值增大到一定程度时，网壳的几何形态也会逐渐偏离原有的球面形态，因此在某些幅值下节点半刚性产生的削弱作用会稍稍偏离整体规律。

表4 几何初始缺陷影响下木网壳整体稳定承载力（单位：kN/m2）Tab.4 Global buckling capacity of K6 reticulated timber shell influenced by initial geometric imperfection （unit：kN/m2）

图16 几何初始缺陷影响Fig.16 The impact of initial geometric imperfection

此外，通过进一步分析不同刚度条件下几何初始缺陷对木网壳稳定承载力的影响，可以发现如下规律：以缺陷幅值为0时对应的稳定承载力为基数，随着初始几何缺陷水平不断提高，网壳稳定承载力折减程度随之增加。上述规律表明采用半刚性节点的木网壳比采用刚接节点的木网壳对初始几何缺陷的变化更为敏感。换言之，几何初始缺陷的存在对半刚性木网壳稳定性能的影响更为不利。

3.4 荷载分布模式影响

有关不同恒活荷载分布模式对半刚性节点稳定性能的具体影响如图17、图18及表5所示。可以看出，随着活荷载与恒荷载比值逐渐增大，节点半刚性木网壳与刚接节点木网壳的稳定承载力均呈现下降趋势。活荷载比例从初值0过渡至终值1的过程中，稳定承载力的变化规律虽较为复杂，但总体上是随着矢跨比数值的减小而逐渐降低，并且Psr与Pr之间的差异也普遍增大。同种荷载分布模式下，相同规格网壳中节点半刚性对木网壳整体稳定承载力的削弱作用普遍存在，并且对应节点半刚性影响系数介于0.58～0.98之间。

图17 荷载分布模式影响Fig.17 The impact of load distribution on buckling capacity

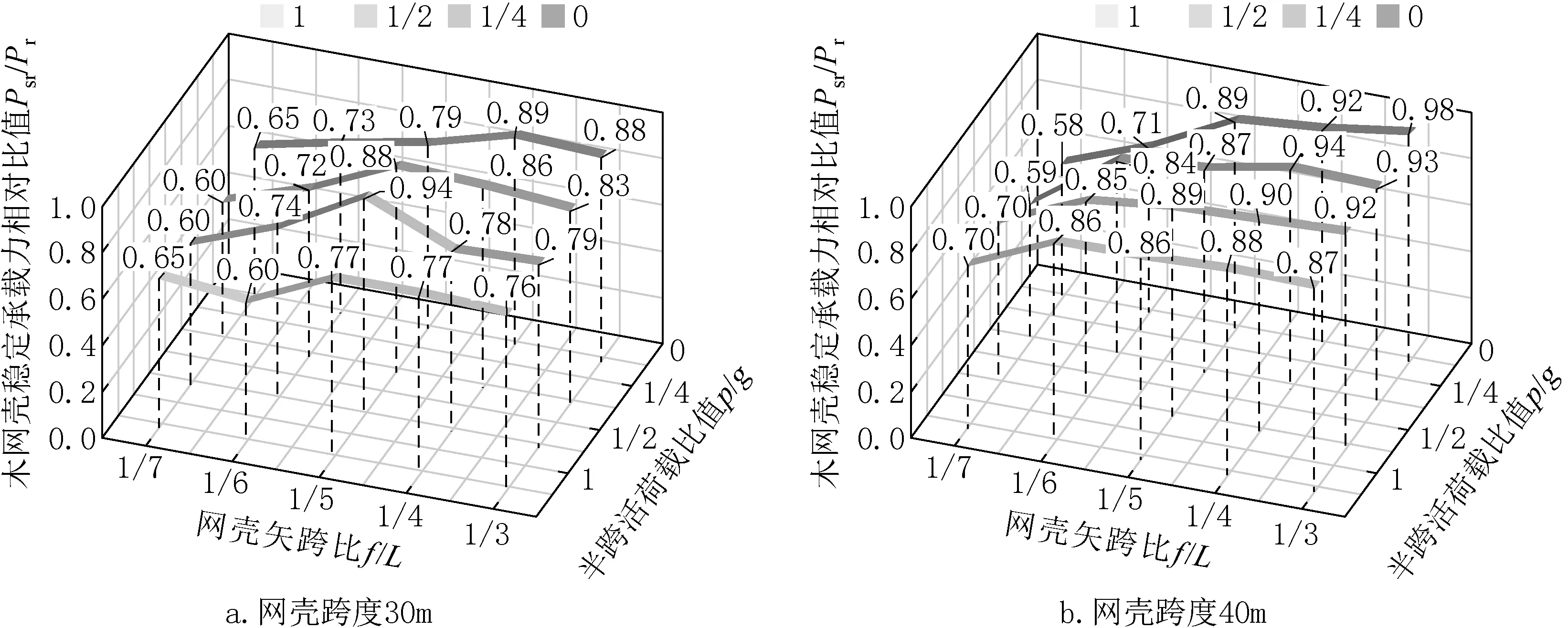
图18 不同荷载分布模式下节点半刚性影响系数Fig.18 Impact factors which joint rigidity causes under the influence of variant load distribution

表5 荷载分布模式影响下木网壳整体稳定承载力（单位：kN/m2）Tab.5 Global buckling capacity of K6 reticulated timber shell influenced by load distribution（unit：kN/m2）

3.5 周边支承条件影响

有关周边支承条件对半刚性节点木网壳稳定性能的具体影响如图19及表6所示。可以看出，当矢跨比数值较小时，半刚性节点木网壳稳定承载力普遍低于刚接节点木网壳稳定承载力；但当矢跨比数值逐渐增大，上述规律不再出现。究其原因，可能是因为周边支承条件变化，会导致木网壳结构的最低阶屈曲模态从局部点失稳状态向整体环状失稳状态过渡，继而影响初始刚度矩阵中各刚度系数分布。通过特征值屈曲分析方法获得网壳最外环节点在三向铰接条件下的最低阶屈曲模态，大致上分为局部点失稳模态、过渡型失稳模型及整体环状失稳模态三类情况。直观上讲，当铰接条件下网壳屈曲模态为局部点失稳模态A时，节点半刚性会对网壳稳定性能产生削弱作用；而对于整体环状失稳模态B来说，节点半刚性对网壳稳定性的影响会表现出时而增强时而削弱的状态。总体上来说周边支承条件变化对木网壳整体稳定承载力影响差异不大。有关木网壳最低阶屈曲模态变化情况如图20所示。

图19 周边支承条件影响Fig.19 The impact of peripheral boundary conditions on buckling capacity

表6 周边支承条件影响下木网壳整体稳定承载力（单位：kN/m2）Tab.6 Global buckling capacity of K6 reticulated timber shell influenced by peripheral boundary conditions（unit：kN/m2）