配筋率对UHPC梁抗弯承载力影响的试验研究

钟宏伟， 郑小红， 宋 琢

（1.华南理工大学土木与交通学院，广州 510640； 2.广州市市政工程机械施工有限公司，广州 510060）

Larrard 和Sedran［1］在1994 年提出了“超高性能混凝土（Ultra High Performance Concrete，UHPC）”概念.UHPC 是一种由各种掺合料和钢纤维组成的新型水泥基复合材料，具有超高强度、超强韧性和极好的耐久性等优势，被称为21 世纪最具有创新性的工程材料，在土木工程尤其是桥梁工程中具有广阔的应用前景［2-4］. 活性粉末混凝土（Reactive Powder Concrete，简称RPC）是其中一种最具代表性的超高性能混凝土材料［5］.

抗弯性能是UHPC梁在工程应用中首先要解决的问题，近几年国内外不少学者展开了相关研究［6-11］，结果表明受拉钢筋配筋率是影响UHPC梁抗弯力学性能最主要的因素. Turker等［6］对12根UHPC梁进行抗弯试验研究，试验表明当钢纤维掺量为1.5%时，配筋率为0.9%、1.9%、2.8%、4.3%的试验梁均发生适筋受弯破坏. 曹霞等［7］通过6根RPC梁的三点加载试验，分析了纵筋配筋率对RPC梁受弯性能的影响，配筋率为4.9%和6.8%的UHPC梁承载力比配筋率3.0%的梁分别提高了26.7%和45.3%. 郑文忠等［8］对6根UHPC梁进行了受弯承载力试验，以配筋率为变量得到了三种不同的受弯破坏形态. 孙明德等［9］对20根RPC梁进行了抗弯性能试验，结果表明：配筋率0.87%以下的试验梁发生少筋破坏，配筋率1.6%～5.66%的梁发生适筋破坏，配筋率9.09%～16.35%的梁发生超筋破坏. 苏家战等［10］进行了12根UHPC梁的抗弯试验研究，试验中配筋率为0.8%、1.8%、3.8%的试件均呈现适筋破坏特征. 梁兴文等［11］对16根UHPC梁进行了抗弯承载力试验研究，试验梁在配筋率3.21%时发生适筋破坏，在配筋率6.74%时发生超筋破坏. 由上述研究可知配筋率是影响UHPC梁破坏模式的直接因素，但目前关于配筋率界限（最小配筋率ρmin、最大配筋率ρmax）的研究十分缺乏.

目前国内尚未有UHPC标准设计规范，相关规程有《活性粉末混凝土结构技术规程》（DBJ 43/T 325—2017）［12］（以下简称《活规》）和《纤维混凝土结构技术规程》（CECS38：2004）［13］（以下简称《纤规》）. 其中《活规》对配筋UHPC 梁的抗弯承载力计算基本假定是不考虑UHPC 的抗拉能力，而实际上作为不同于普通混凝土的新材料，UHPC掺合料中的钢纤维对抗弯承载力有一定的贡献，是否可以忽略需进一步探讨.《纤规》主要针对的是普通钢纤维混凝土梁的抗弯承载力计算，计算参数均是根据普通混凝土的力学性能进行取值确定，因此对于公式中具体参数的取值需要重新确定. 徐海宾［14］基于UHPC的本构关系计算得到等效应力矩形系数α与β 值分别为0.9与0.7，并考虑了钢纤维的抗拉贡献建立了极限承载力平衡方程. 潘琦等［15］将UHPC的弯曲极限压应变和轴心受压峰值压应变比值设为v后根据力的平衡条件推导了UHPC梁的抗弯承载力计算公式. 马熙伦等［16］从钢纤维的抗拉性能出发，将UHPC受压区等效为三角形、受拉区等效为不规则四边形进行应力图形积分计算，推导了不同钢纤维掺量下的UHPC梁抗弯承载力的计算方法. 由于目前还尚未有统一的计算方法，受拉区UHPC抗拉能力如何合理计算，还需要更多研究.

因此，本文考虑了6种不同配筋率的UHPC梁，以及2根用来做对比的RC梁，通过四点弯曲试验，对不同配筋率的UHPC 梁破坏模式以及抗弯承载力进行研究，以建立配筋率的界限值和抗弯承载力计算公式，为UHPC梁的应用和设计提供参考和依据.

1 试验概况

1.1 材料

UHPC 原材料有水泥、硅灰、石英砂、减水剂、钢纤维和水. 水灰比为0.18，其中石英砂粒径为0.25～0.45 mm，钢纤维体积掺量为2%，直径为0.2 mm、长度为13 mm、抗拉强度约为2800 MPa. 参考《活性粉末混凝土》（GBT 31387—2015）［17］和《超高性能混凝土基本性能与试验方法》（T/CBMF 37—2018）［18］，UHPC材料在标准条件养护下，测得28 d的立方体抗压强度fcu平均值为105.2 MPa，抗拉强度ft平均值为7.6 MPa. 受拉纵筋采用HRB400级钢筋，直径为12、18、20、22 mm，试验测得钢筋屈服强度、极限强度和弹性模量分别为445、615 MPa和200 GPa. 架立筋和箍筋采用HPB300级钢筋，直径为8 mm.

1.2 试件分组

按照纵筋配筋率不同，设计了6组共18条UHPC梁，并设置了1组（MA）普通钢筋混凝土梁（C40）作为对比试件. 所有试验梁尺寸相同，长度为1850 mm，高度为200 mm，宽度为100 mm. MB 组为无筋UHPC 梁，MC组共有5种不同的纵筋配筋率，分别为1.32%、3.03%、6.83%、8.54%、10.56%，除了无筋的MB组，其他组还配有2根直径8 mm（2φ8）的架立筋和直径8 mm、间距100 mm（φ8@100）的箍筋，混凝土保护层厚度为15 mm.梁具体钢筋配置和几何尺寸见图1所示. 试件编号及配筋率变化如表1所示.

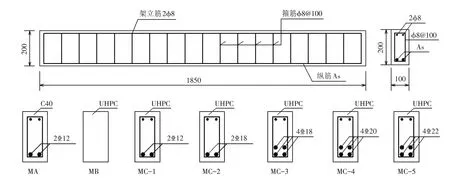
图1 试验梁配筋图Fig.1 Reinforcement details of specimens

表1 试件分组Tab.1 Specimen grouping

UHPC梁的制作步骤为：干料加入一半水，搅拌2 min；加入剩下的一半水，搅拌6 min；加入减水剂和钢纤维，搅拌2 min，搅拌完成后从模板的一侧开始浇筑成型，用塑料薄膜和麻袋进行保温保湿，2 d拆模后每日浇水养护至28 d.

1.3 加载及测试方案

本次试验采用四点弯曲加载、位移控制方式，加载速率为0.05 mm/s. 加载设备为电液伺服结构试验系统，型号JAW-500A，最大压力值为500 kN. 梁跨中截面、支座截面、加载点位置共布置了5个位移计，梁跨中截面沿着梁高间隔40 mm在混凝土表面粘贴了电阻应变片，数据采集设备为DH3816静态应变仪采集系统，自动记录应变、荷载和位移值. 加载及测试方案如图2所示.

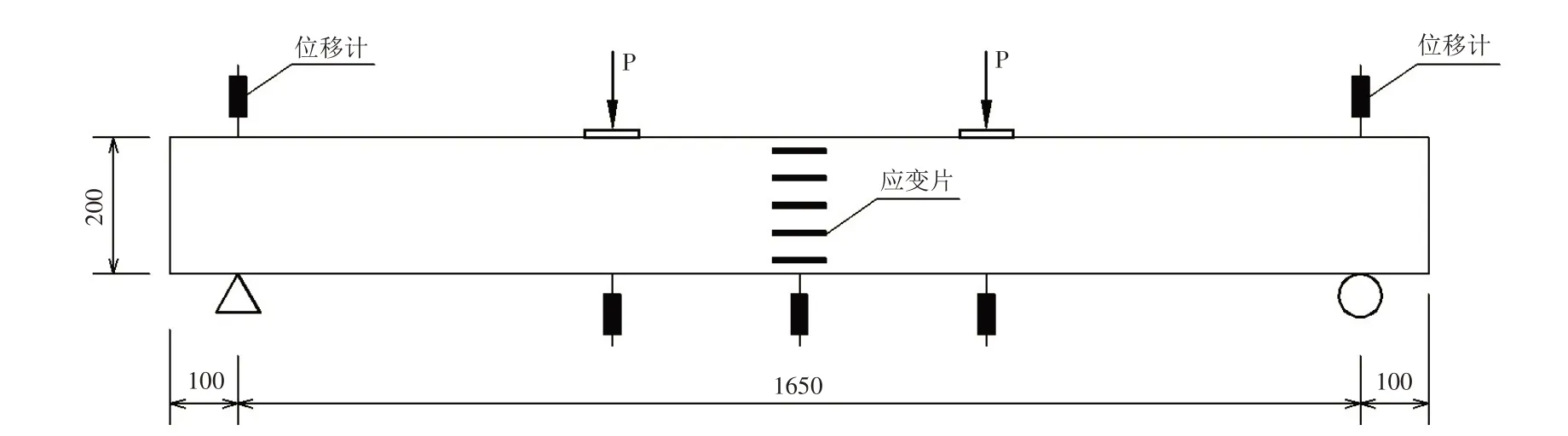
图2 试验梁加载及测试方案示意图（单位：mm）Fig.2 Schematic diagram of loading and test scheme of specimens

2 试验结果

2.1 破坏模式

对比试件MA组（1.32%）的2根RC梁出现了典型的适筋受弯破坏特征，如图3a所示，在纯弯段出现少量的竖向裂缝，随着荷载继续增加，受拉钢筋屈服后受压区混凝土压碎，RC梁破坏.

UHPC试验梁随着配筋率不同，出现了少筋、适筋和超筋破坏三种破坏形态，裂缝的分布如图3b～d所示.

MB组（0%，无筋）为素UHPC梁，表现为明显的少筋脆性破坏模式特征. 加载前期，在弹性阶段无明显裂缝出现，当加载至30 kN左右时，在跨中位置出现几条微裂缝，右侧加载点处开始出现一条主裂缝；继续加载至35～40 kN时，主裂缝贯通整个梁截面，试验梁破坏，最终跨中挠度只有2 mm左右.

MC-1（1.32%）和MC-2（3.03%）组表现为适筋梁破坏特征如图3c所示. 适筋UHPC梁的纯弯段首先开裂，随着荷载的增大，受拉区开始出现多条竖向裂缝，竖向裂缝不断发展，随着受拉钢筋屈服，中性轴不断上移，受压区UHPC应变持续增加并在受压区开始出现水平裂缝. 但是由于钢纤维的“桥联”作用，受压区UHPC裂而不散、坏而不碎，始终保持整体，具有很好的延性.

MC-3（6.83%）、MC-4（8.54%）、MC-5（10.56%）三组试验中出现了超筋破坏模式如图3d所示. 试验梁开裂后纯弯段竖向裂缝不断发展延伸且加载挠度较大时弯剪段也开始出现了紧密的斜裂缝，UHPC梁底部开裂、钢纤维不断被拔出后受压区混凝土逐渐被压碎，此时受拉钢筋仍未屈服，随着试验梁挠度持续增大，混凝土突然剥落，而后受压区混凝土被完全压碎，试验梁破坏，超筋梁的裂缝更多更细.

图3 试验梁典型破坏模式Fig.3 Typical failure modes of specimens

2.2 荷载-位移曲线

各组试验梁的荷载-跨中位移曲线如图4所示，表2是各组的特征荷载和位移平均值，参考文献［19］中梁延性的分析方法，用位移延性系数μ△表示梁的延性大小，μ△=△u/△y，其中△u是梁达到极限承载力时对应的位移，△y是屈服位移.

表2 特征荷载及其位移Tab.2 Characteristic loads and their displacements

从表2和图4的荷载-位移曲线可知：

1）尽管没有配筋，但UHPC梁（MB-1组）的开裂荷载还是比普通RC梁（MA-1组）提高了将近1倍. MC组配筋UHPC梁的开裂荷载比对比RC梁提高了29%～53%. 主要是因为UHPC梁内的钢纤维能大大提高梁的抗裂性能.

2）对于适筋破坏的UHPC梁MC-1组（1.32%）、MC-2组（3.03%），随着配筋率的提高，其屈服荷载分别比RC梁（MA-1）提高了41.5%和158.5%.

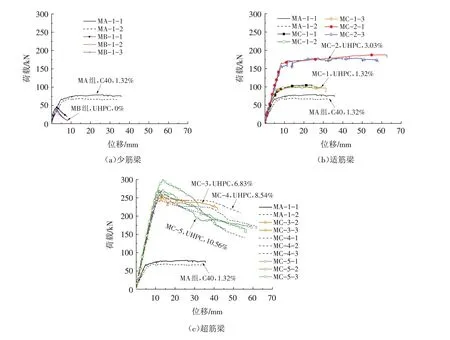
图4 荷载-跨中位移曲线Fig.4 Loading-displacement curves at mid-span

3）无筋UHPC 梁（MB-1）的极限承载力大约是RC 梁极限承载力的53%，是适筋梁MC-1 组承载力的39.4%. 可见，对于UHPC梁来说，受拉区混凝土的抗拉能力对于极限承载力的贡献不能忽略.

4）随着配筋率的增加，UHPC 梁的极限承载力逐渐增加. 对于适筋破坏的MC-1、MC-2 组，配筋率从1.32%增加至3.03%，极限承载力分别比RC 梁（MA-1）提高了35.1%、134.5%. 对于超筋破坏的，MC-3、MC-4、MC-5 组（配筋率分别为6.83%、8.54%、10.56%），极限承载力分别比RC 梁（MA-1）提高了243.2%、256.1%、276.2%.

5）无筋的MB组、超筋的MC-3～MC-5组发生了脆性破坏；MA组、MC-1组、MC-2组发生适筋破坏. 根据以上延性系数的定义，UHPC梁的延性系数略高于普通混凝土梁，这是由于梁体开裂时，钢纤维拔出做功吸收了断裂能使其延性得到了提升. 随着UHPC梁配筋率从1.32%增加至3.03%，UHPC梁的延性系数提高了52.1%. 可以看出，对于适筋范围的UHPC梁，增加纵筋配筋率可以大幅提高UHPC梁的延性.

6）MC-3～MC-5组为超筋UHPC梁，其极限荷载均在250～300 kN之间. 对于超筋UHPC梁，随着配筋率的增加，极限承载力提升幅度很小，试验梁表现为明显的脆性破坏.

2.3 跨中截面应变分布

图5是UHPC梁在典型破坏模式下跨中截面沿高度方向的应变分布，可见，加载过程中试验梁的跨中截面应变沿高度方向分布近似为直线，满足变形协调条件，截面应变符合平截面假定.

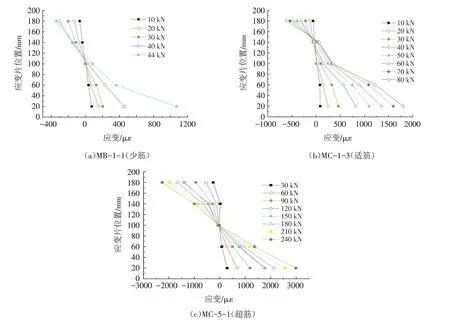
图5 部分试验梁跨中截面应变分布图Fig.5 Strain profiles at mid-span sections of some specimens

3 配筋UHPC梁抗弯承载力计算

3.1 《活规》公式计算界限配筋率

就目前而言，国内UHPC梁的抗弯承载力计算相关标准仅有湖南省的《活性粉末混凝土结构技术规程》（DBJ 43/T 325—2017），第6.3条规定UHPC受弯构件最小配筋率为

其中：ft是UHPC的抗拉强度，本试验中为7.6 MPa；fy是钢筋的屈服强度，取值为445 MPa. 代入上式中，得到本次试验中UHPC梁的最小配筋率为0.77%.

关于最大配筋率ρmax，《活规》中规定对于配筋UHPC受弯构件，其界限相对受压区高度ξb为

其中：α1是等效矩形应力图形系数；fc是UHPC轴心抗压强度. 根据（3）式计算得ρmax=7.51%，而在本文试验中，配筋率为6.83%的MC-3组破坏模式为超筋破坏，因此《活规》中的界限配筋率规定与本文的试验结果有一定偏差.

3.2 《活规》公式计算抗弯承载力

《活规》第4.1 节对UHPC 梁抗弯承载力作出规定，基本假定为极限状态时，不考虑构件截面受拉区活性粉末混凝土的抗拉作用，抗弯承载力计算公式与普通RC 梁类似. 表3 是本次试验的15 根UHPC 梁采用《活规》中的承载力计算公式得到的抗弯承载力理论计算值Mu与抗弯承载力试验值Mexp对比.

可见，由于《活规》的抗弯承载力计算公式中未考虑钢纤维受拉作用的影响，规范公式计算值比试验值偏小30%～40%. 根据文献［20］，钢纤维对适筋UHPC 梁抗弯承载力贡献约为极限值的15%～40%，如果忽略不计，在计算最大配筋率和极限承载力时有一定误差，因此对于适筋UHPC 梁，为了能更准确地计算梁实际的抗弯承载力，应考虑钢纤维的受拉作用.

3.3 UHPC梁抗弯承载力修正计算公式

参考《纤规》中的受弯构件承载力计算模式，建立UHPC梁的计算简图如图6所示，本文提出配筋UHPC梁抗弯承载力计算公式

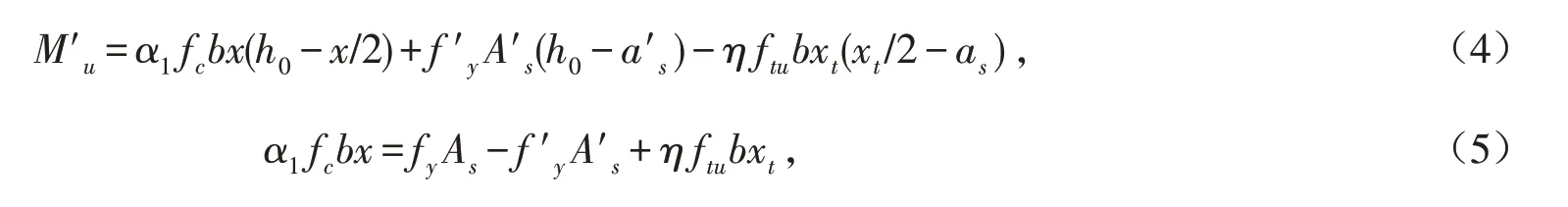
表3 配筋UHPC梁抗弯承载力对比Tab.3 Comparison of flexural capacities of reinforced UHPC beams

式中：η 为考虑受拉区UHPC 抗拉性能对抗弯承载力贡献的修正系数，偏于安全考虑，提出修正系数η 为0.53；α1为受压区等效矩形应力图形系数，按《活规》中表4.1.2-1的规定进行取值；β1为等效矩形应力图块的受压区高度折减系数；fc为UHPC轴心抗压强度；x为受压区等效矩形应力图形的高度；xt为受拉区等效矩形应力图形高度；ftu为受拉区UHPC等效矩形应力图形的抗拉强度，计算公式同《纤规》；fy、f′y为受拉、受压钢筋强度；As、A′s为受拉、受压钢筋截面面积；as、a′s为纵向受压、受拉钢筋合力点距截面边缘的距离；b、h 为截面宽度和高度；h0为截面有效高度. 则最大配筋率计算公式为

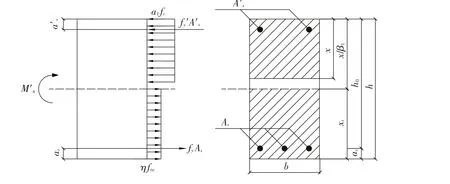
图6 配筋UHPC梁计算简图Fig.6 Calculation diagram of reinforced UHPC beam

根据式（6）可得本次试验条件下的最大配筋率ρmax=6.43%，即试验中MC-3～MC-5组均为超筋梁，与试验结果吻合.

采用本文提出的抗弯承载力计算公式，对MC-1、MC-2组进行适筋梁抗弯承载力计算并与试验值进行对比，如表4所示，表中M′u为公式（4）和（5）计算的抗弯承载力计算值.

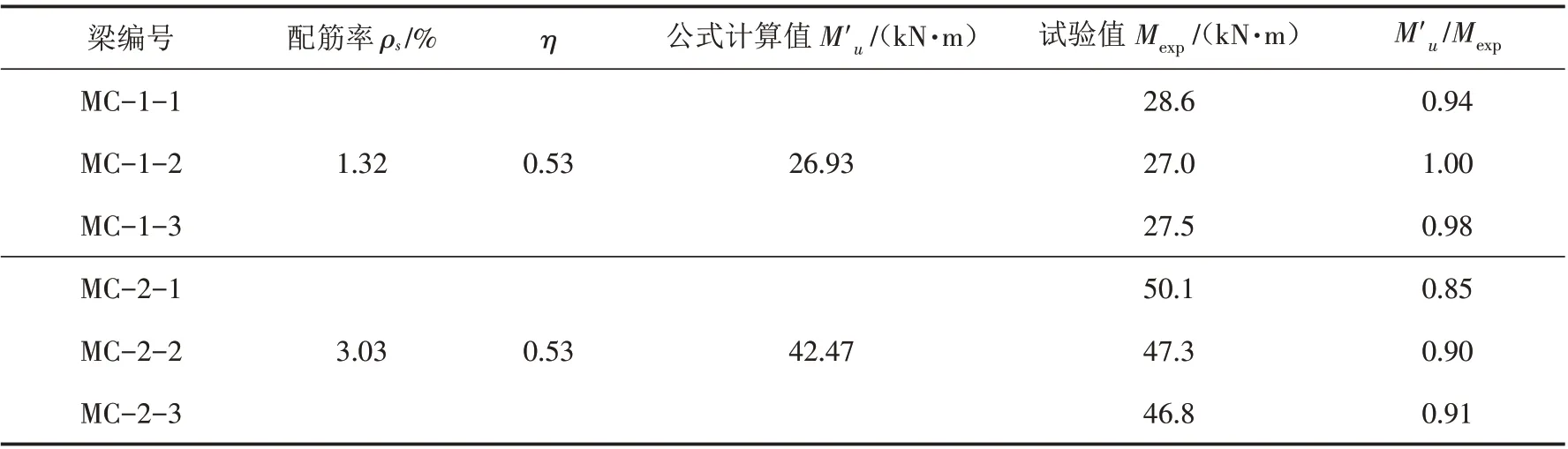
表4 采用修正后公式计算结果Tab.4 The calculation results used by modified formula

由表4可知，采用修正公式计算的M′u/Mexp均值为0.93，标准差为0.05，变异系数为5.46%，抗弯承载力的计算值和试验值吻合较好，采用本文提出的计算公式对于适筋UHPC梁的最大配筋率和抗弯承载力的计算具有良好的适用性.

4 结论

为探讨配筋率对UHPC梁抗弯承载力的影响，设置6种配筋率，进行了18根UHPC梁和2根RC梁的四点弯曲试验，分析了破坏模式、承载力和应变等数据，得到如下结论：

1）和同配筋率的RC梁相比，UHPC梁开裂荷载、屈服荷载和极限荷载分别提高了29%、41.5%和35.1%.

2）无筋UHPC梁（MB组）发生典型的少筋梁脆性破坏，极限承载力约为适筋梁MC-1组承载力的39.4%，受拉区混凝土的抗拉能力对于极限承载力的贡献不能忽略；配筋率为1.32%、3.03%的MC-1，MC-2组发生适筋破坏特征；配筋率分别为6.83%、8.54%、10.56%的MC-3～MC-5的试件发生超筋破坏，裂缝细而密.

3）随着纵筋配筋率的提高，UHPC 梁的极限承载力不断增加. 相较于MC-1 组（ρ=1.32%）的UHPC 梁，MC-2～MC-5 组（ρ=3.03%～10.56%）的UHPC 梁的极限承载力（各组的平均值）分别提高了73.5%、153.9%、163.5%、178.4%. 当UHPC梁发生超筋破坏后，随着配筋率的增加，承载力提高幅度较小.

4）现行相关技术规程由于未考虑钢纤维抗拉能力，关于UHPC梁的抗弯承载力理论计算值比试验值偏低30%～40%，最大配筋率ρmax计算值比试验结果偏大. 本文参考《纤规》中的计算模式，考虑受拉区钢纤维对抗弯承载力的贡献，提出承载力修正系数η，得到修正后的最大配筋率界限值以及抗弯承载力计算值与试验值更吻合.