塑性铰区纵向配筋率变化对重力式桥墩抗震性能的影响

2020-10-15鲁锦华陈兴冲丁明波张熙胤马华军

铁道科学与工程学报 2020年9期

鲁锦华，陈兴冲，丁明波，张熙胤，马华军

鲁锦华，陈兴冲，丁明波，张熙胤，马华军

(兰州交通大学土木工程学院，甘肃兰州 730070)

针对弯曲破坏型桥墩在地震中仅在墩底塑性铰区内发生严重破坏的情况，提出一种纵向钢筋的布置方法，即仅在墩身底部(2倍塑性铰长度)增加纵向钢筋的数量，其余墩身部位钢筋数量保持不变。设计了5个桥墩，运用ANSYS 软件分析了墩身底部配筋率的变化对桥墩抗震性能的影响。研究结果表明：仅提高墩身底部配筋率，可以提高桥墩的承载能力，增强桥墩的耗能能力，增大桥墩的位移延性；与传统相同配筋率的桥墩相比，滞回曲线“捏缩”较为严重；提高低配筋率桥墩底部配筋率，桥墩的抗震性能基本可以达到全截面高配筋率桥墩的抗震性能。

重力式桥墩；配筋率；塑性铰区；抗震性能

墩柱是桥梁结构中非常重要的部件，主要作用是传递竖向力和承受水平荷载[1−2]。在已发生的地震灾害调查中，桥墩是在地震荷载作用下容易受损的构件，而且一旦桥墩受损严重，将导致整个桥梁无法使用[3−4]。因此保证桥墩的抗震性能对桥梁的安全尤为重要。自从20世纪60年代起，美国、新西兰和日本等国开始对桥墩的抗震性能进行试验研究[5−7]。根据试验结果分析得到了影响桥墩抗震性能的主要因素：轴压比、剪跨比、配箍率，混凝土强度和配筋率等。而对于少筋混凝土铁路重力式桥墩而言，桥墩仅配置有护面钢筋，配筋率较低，因此配筋率成为了影响桥墩抗震性能的主要因素。国内学者对其进行了深入的研究，蒋丽忠等[8]对配筋率为0.15%、0.45%和0.75%的高速铁路桥墩进行了拟静力试验研究，发现随着配筋率的增加，桥墩的滞回曲线越来越饱满，耗能能力增强，刚度增大，承载能力增大。鞠彦忠等[9−10]对配筋率为0.1%和0.2%的圆端形截面铁路桥墩进行了往复循环荷载试验，分析了配筋率的变化对桥墩的滞回曲线、耗能及延性等性能的影响。陈兴冲等[11−12]研究了配筋率对矩形截面桥墩抗震性能的影响，得到了罕遇地震下铁路桥墩在不同烈度下的最小配筋率。在以上研究中，模型桥墩纵向钢筋均贯穿整个墩身。在汶川地震[13]、玉树地震[14]及九寨沟地震[15]等大震中发现，发生弯曲型破坏的桥墩，严重破坏部位主要集中在桥墩底部塑性铰区内，塑性铰区以上部位未见混凝土剥落等严重破坏的情况。桥墩塑性铰区以上部位的纵向钢筋受力偏小，富余量较多，造成了一定的浪费。针对这个问题，本研究对配筋率较低的铁路弯曲破坏型桥墩提出了一种新的纵向钢筋布置方法，即只在塑性铰区范围内增加纵向钢筋的数量，塑性铰区以上截面纵向钢筋数量保持不变。以配筋率为0.3%的桥墩为基准设计了3个塑性铰区配筋率变化的桥墩，同时设计了相应的对照组，验证仅提高塑性铰区配筋率桥墩的抗震性能是否能到达对应的全截面高配筋率(增加后)桥墩的抗震性能。

1 桥墩参数设计

为研究塑性铰区配筋率变化对桥墩抗震性能的影响，设计了5个桥墩，在配筋率为0.3%桥墩的基础上仅提高塑性铰区高度范围内的配筋率，分别为0.4%和0.5%，塑性铰区高度以上截面配筋率保持0.3%不变，另外分别设计一个全截面配筋率为0.4%和0.5%的对比桥墩，用以对比分析仅塑性铰区配筋率变化对桥墩抗震性能的影响。5个桥墩的纵向钢筋直径为8 mm，箍筋直径为6 mm，间距为100 mm，混凝土强度等级为C30，钢筋选用HRB335。塑性铰长度按《公路桥梁抗震细则》中塑性铰长度计算公式取值，取加载方向截面宽度的2/3倍，考虑到因局部纵筋加密会致使破坏面转移的情况，墩身底部加密纵筋的高度取塑性铰长度的2倍。加密区钢筋的下部构造与通长钢筋保持一致，上部端头处做弯钩处理(见图1)，以确保钢筋与混凝土共同作用。桥墩具体参数见表1，桥墩尺寸见图1及截面配筋见图2。

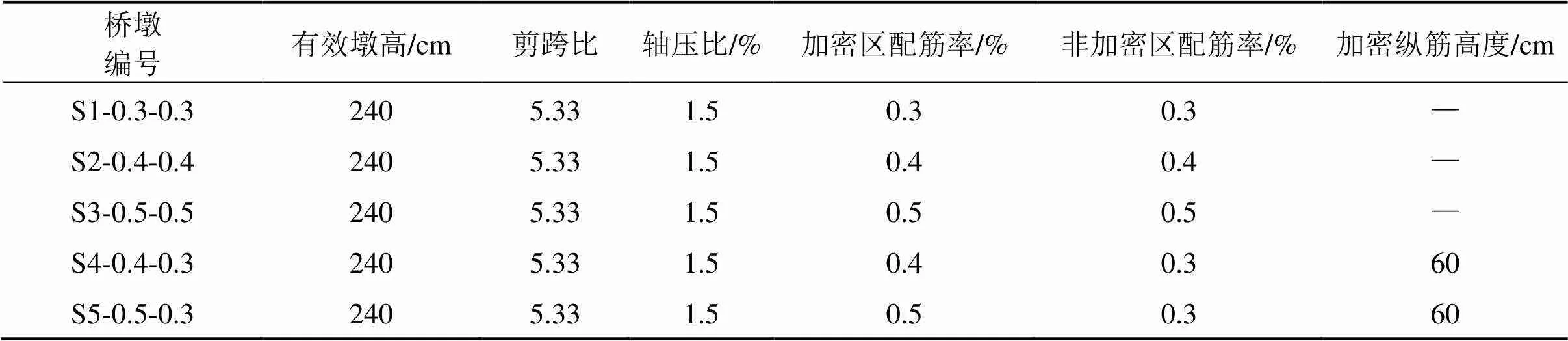
表1 桥墩设计参数

注：S-加密区配筋率−非加密区配筋率。

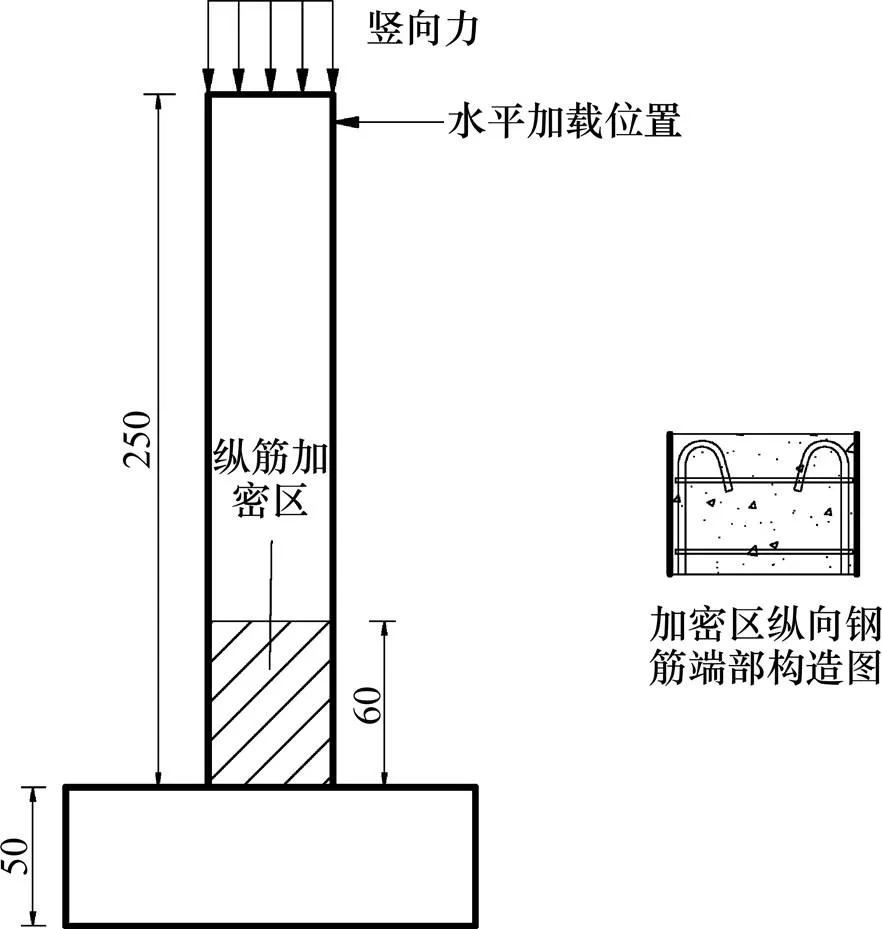
单位：cm

2 材料本构关系

2.1 混凝土本构模型

约束混凝土的本构影响着模型计算时混凝土受压强度的大小，同时也决定着混凝土受压破坏的全过程。选用Mander本构模型[16]。模型中，混凝土强度等级为C30，抗压强度标准值为20.1 MPa，应力−应变曲线根据Mander模型进行计算。

2.2 钢筋的本构关系

钢筋的本构关系对桥墩滞回曲线的形状有着重要的影响。国内外学者[17−19]研究发现钢筋的包辛格效应可以更好的反应滞回曲线的“捏缩”效应，并提出了更能够反应钢筋包辛格效应的本构关系。选用ANSYS中提供的可以反应钢筋包辛格效应的多线性随动强化模型(KINH)。模型中，钢筋采用HBR335级，屈服强度和极限强度分别为335 MPa和490 MPa，弹性模量为2.1×105MPa。

2.3 钢筋与混凝土之间的黏结−滑移关系

在循环荷载作用下，随着桥墩墩顶位移的增加，钢筋和混凝土之间会产生一定的滑移。钢筋和混凝土之间的滑移关系对桥墩的承载力和滞回曲线的形状都有一定的影响，从国内外学者的研究中可以发现，考虑钢筋与混凝土之间的黏结−滑移关系后，桥墩的承载力会降低，滞回曲线的“捏缩”效应更加显著[20−21]。选用弹塑性黏结−滑移本构模型[22]。

3 桥墩抗震性能分析

3.1 滞回曲线

选用上述材料本构，利用ANSYS软件对5个桥墩进行计算，混凝土选用SOLID65单元进行模拟，钢筋选用LINK180单元进行模拟和黏结滑移选用COMNBIN39单元进行模拟，其中COMNBIN39单元相关参数取值分别为：KEYOPT (1)取1，KEYOPT(2)取0，KEYOPT(3)取2，KEYOPT (4)取0。为了考虑箍筋对混凝土的约束效应，采用文献[19]中给出的扩大的破坏面进行模拟，即定义混凝土破坏准则时，其抗压强度提高1.2~ 2倍。模型桥墩的网格尺寸大小取50 mm×50 mm×50 mm，既能保证计算精度，也可确保其收敛[23−24]。墩顶上部荷载按面荷载施加，水平加载采用位移控制。模拟得到桥墩的滞回曲线，如图3所示。

(a) S1-0.3-0.3和S4-0.4-0.3滞回曲线对比；(b) S1-0.3-0.3和S5-0.5-0.3滞回曲线对比；(c) S2-0.4-0.4和S4-0.4-0.3滞回曲线对比；(d) S3-0.5-0.5和S5-0.5-0.3滞回曲线对比

从图3(a)和3(b)滞回曲线对比中可以看出：仅提高墩身底部配筋率可以提高桥墩的承载力和极限位移。从图3(c)和3(d)中可以看出，S4-0.4-0.3桥墩的滞回曲线基本与S2-0.4-0.4桥墩的重合，S5- 0.5-0.3桥墩的滞回曲线基本与S3-0.5-0.5桥墩的重合，说明提高低配筋率桥墩墩身底部的配筋率，桥墩的抗震性能基本可以达到全截面高配筋率(增加后)桥墩的抗震性能。但是加载后期，由于墩身非加密区截面钢筋数量的较少，钢筋与混凝土之间发生黏结滑移时桥墩总的黏结应力较小，以至于墩身底部纵筋加密桥墩的滞回曲线与全截面高配筋率桥墩相比有明显的“捏缩”效应，从图3(c)和3(d)中可以明显的观察到。

3.2 骨架曲线

骨架曲线是桥墩在循环荷载作用下得到的滞回曲线的外包络线，即墩顶力−位移曲线，可以很好地反映桥墩的承载能力和变形等变化规律。根据滞回曲线得到桥墩的骨架曲线如图4所示。

由图4(a)骨架曲线对比图中可以看出，S4-0.4- 0.3桥墩的峰值荷载大于S1-0.3-0.3桥墩的峰值荷载，S5-0.5-0.3桥墩的峰值荷载大于S4-0.4-0.3桥墩的峰值荷载，说明仅提高墩身底部配筋率可以很好地提高桥墩的承载能力。同时还发现随着墩身底部配筋率的提高，桥墩的极限位移不断增大。图4(b)和4(c)中可以看出，加载初期，2条曲线基本完全重合，主要因为加载初期墩顶位移较小，钢筋处于弹性阶段且非加密区纵向钢筋基本没有发挥作用；随着加载位移的增大，二者的差值逐渐增大，由于钢筋屈服，且非加密区钢筋数量较少，对水平承载力的贡献减小，以至于S4-0.4-0.3桥墩的水平承载力略小于S2-0.4-0.4桥墩的水平承载力，S5-0.5-0.3桥墩的水平承载力略小于S3-0.5-0.5桥墩的水平承载力，但是二者的最大偏差仅有7%。说明提高墩身底部配筋率，桥墩基本可以达到全截面高配筋率(增加后)桥墩的承载能力。

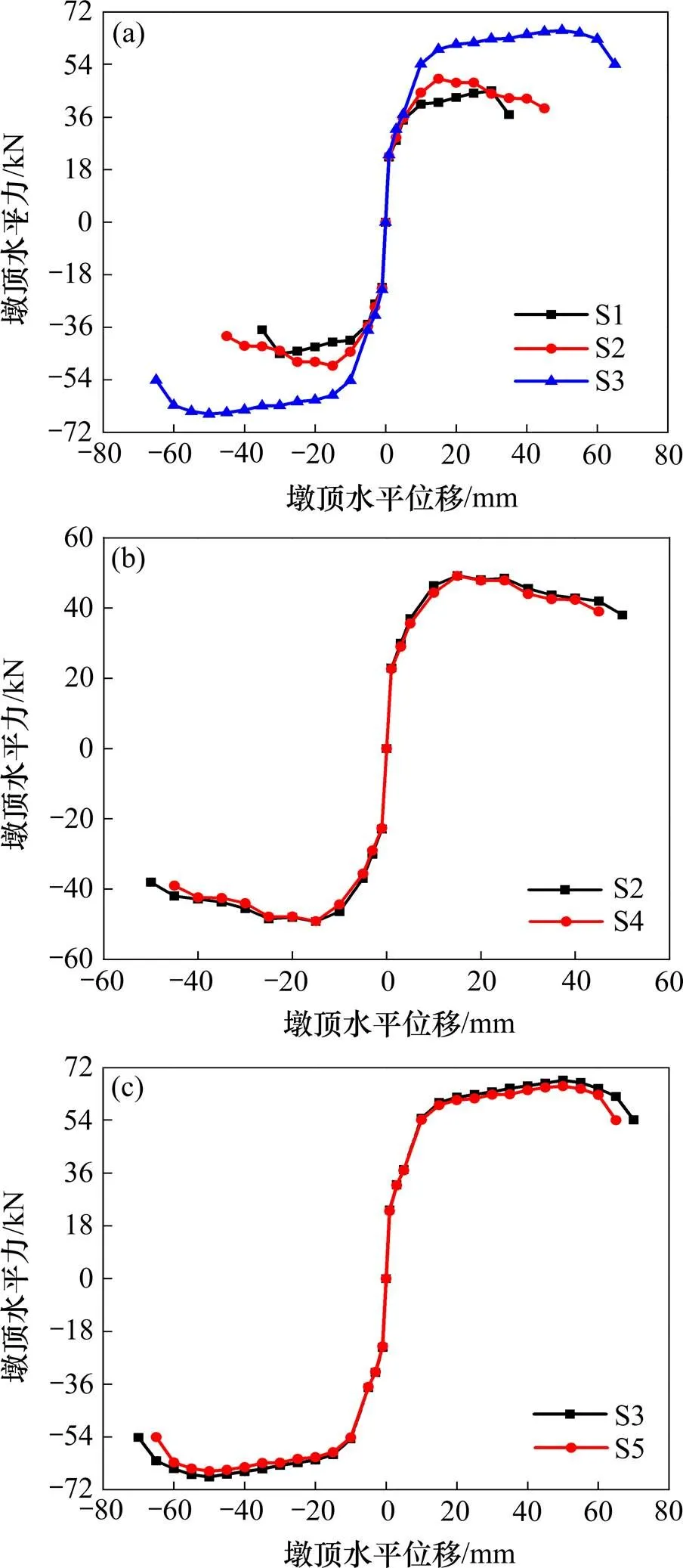
(a) S1-0.3-0.3，S4-0.4-0.3和S5-0.5-0.3对比图；(b) S2-0.4-0.4和S4-0.4-0.3对比图；(c) S3-0.5-0.5和S5-0.5-0.3对比图

3.3 位移延性

位移延性系数是评价桥墩抗震性能的重要指标，桥墩的极限位移与屈服位移的比值即是位移延性系数。桥墩的屈服位移采用Park法[25]进行计算，极限位移取桥墩承载力下降到峰值的85%时对应的位移，计算得到桥墩的屈服位移和极限位移，见表2所示。

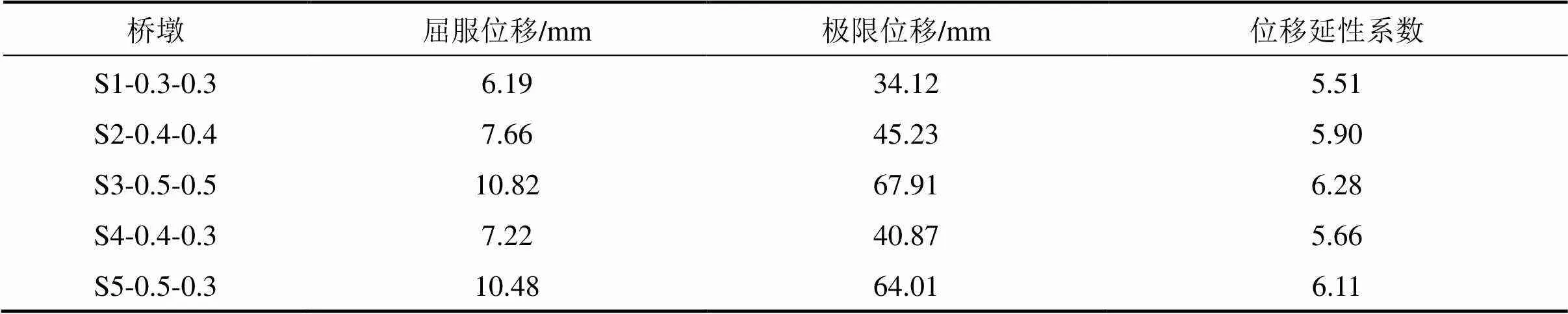
表2 位移延性系数

从表2中可以看出，随着墩身底部配筋率的增加，桥墩的屈服位移和极限位移不断增大，位移延性系数也随着增大；对比S4-0.4-0.3和S2-0.4-0.4及S5-0.5-0.3和S3-0.5-0.5两组数据可以发现，由于非加密区钢筋数量较少，仅提高墩身底部配筋率桥墩的屈服位移和极限位移相比于全截面高配筋率(增加后)桥墩的屈服位移和极限位移均略有减小，位移延性系数也略有减小，但是减小幅度不明显。

3.4 耗能性能

桥墩的耗能能力是指桥墩在荷载作用下发生塑性变形而吸收能量的能力，也是评价桥墩抗震性能的重要指标。累计耗能是根据力−位移曲线所包围的面积来计算的[26]，具体计算见图5所示。依据图5所示计算得到各桥墩的累积耗能随位移的变化曲线，如图6所示。

图5 累计耗能计算图示

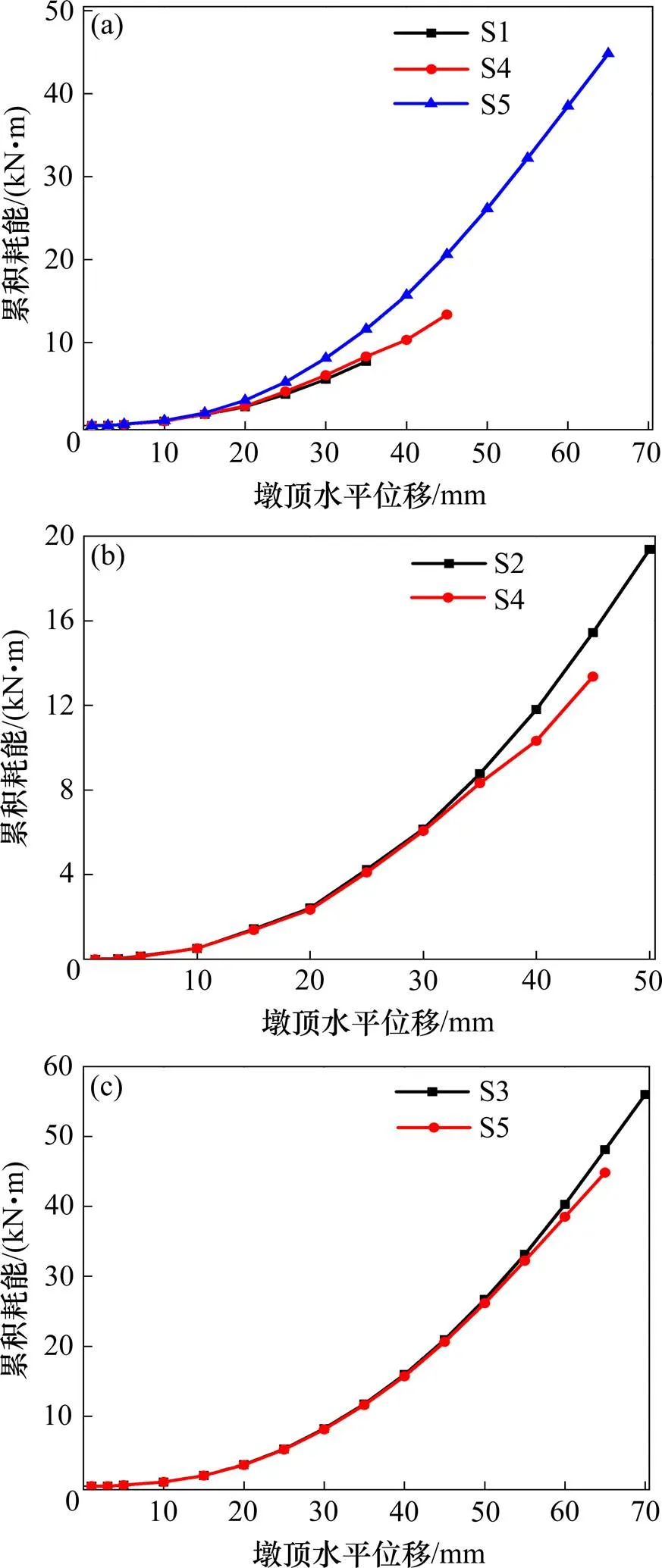
(a) S1-0.3-0.3，S4-0.4-0.3和S5-0.5-0.3对比图；(b) S2-0.4-0.4和S4-0.4-0.3对比图；(c) S3-0.5-0.5和S5-0.5-0.3对比图

从图6(a)可以看出，S4-0.4-0.3桥墩的累积耗能大于S1-0.3-0.3桥墩的累积耗能，S5-0.5-0.3桥墩的累积耗能大于S4-0.4-0.3桥墩的累积耗能，说明仅提高墩身底部配筋率可以很好地提高桥墩的耗能能力。且相同加载位移下墩身底部配筋率越高，桥墩的累积耗能越多。图6(b)可以看出墩顶加载位移小于35 mm时，S4-0.4-0.3 和S2-0.4-0.4桥墩的累积耗能基本相同；当加载位移大于35 mm时，S4- 0.4-0.3桥墩的累积耗能小于S2-0.4-0.4桥墩的累积耗能。图6(c)可以看出墩顶加载位移小于55 mm时，S5-0.5-0.3 和S3-0.5-0.5桥墩的累积耗能基本相同；当加载位移大于55 mm时，S5-0.5-0.3桥墩的累积耗能小于S3-0.5-0.5桥墩的累积耗能。主要原因是桥墩进入塑性阶段之后，S4-0.4-0.3桥墩非加密区纵向钢筋数量较少，桥墩的黏结滑移较大，以至于桥墩的滞回曲线“捏缩”严重，导致耗能减小。

(a) S1-0.3-0.3，S4-0.4-0.3和S5-0.5-0.3对比图；(b) S2-0.4-0.4和S4-0.4-0.3对比图；(c) S3-0.5-0.5和S5-0.5-0.3对比图

3.5 刚度退化

由图7(a)可以看出，桥墩的初始刚度随着塑性铰区配筋率的增加而增加，且相同加载位移下，塑性铰区配筋率越高，桥墩的刚度越大。图7(b)和7(c)中可以看出，S2-0.4-0.4桥墩和S4-0.4-0.3桥墩刚度基本相同，S3-0.5-0.5桥墩和S5-0.5-0.3桥墩刚度基本相同。桥墩的破坏主要集中在塑性铰区，非塑性铰区基本不发生破损，这两组桥墩虽然在非加密区纵向配筋率不同，但是在塑性铰区桥墩的纵向配筋率相同，所以桥墩的刚度基本相同。所以仅提高墩身底部配筋率的桥墩与全截面高配筋率桥墩相比，桥墩的刚度基本保持不变。

4 结论

1) 桥墩的承载能力、屈服位移和极限位移随着2倍塑性铰区配筋率的增加而增加；仅墩身底部配筋率提高的桥墩与全截面高配筋率桥墩相比，滞回曲线“捏缩”效应较为严重，且屈服位移和极限位移偏小。

2) 桥墩的累积耗能、刚度和位移延性系数随着墩身底部纵向配筋率的增加而增大。

3) 提高低配筋率桥墩2倍塑性铰区的配筋率，桥墩的抗震性能基本可以达到全截面高配筋率(增加后)桥墩的抗震性能。

[1] 陈惠发, 段炼. 桥梁工程抗震设计[M]. 北京: 机械工业出版社, 2008. CHEN Huifa, DUAN Lian. Bridge engineering seismic design[M]. Beijing: China Machine Press, 2008

[2] NI S, WANG W, LI L. The April 14th, 2010 Yushu earthquake, a devastating earthquake with foreshocks[J]. Sci China Earth Sci, 2010, 53(6): 791−793.

[3] Jennings P C. Engineering features of the San Fernando earthquake of February 9,1971[R]. Report No. EERL-71- 02 Pasadena: Earthquake Engineering Research Technology Laboratory, California Institute of Technology.

[4] Moehle J P. Northridge earthquake of January 17, 1994: reconnaissance report, volume 1-highway bridges and traffic management[J]. Earthquake Spectra, 1994, 11(3): 287−372.

[5] Jaradat O A, McLean D I, Marsh M L. Performance of existing bridge columns under cyclic loading-part 1: Experimental results and observed behavior[J]. ACI Structural Journal, 1998, 95(6): 695−704.

[6] Jaradat O A, McLean D I, Marsh M L. Performance of existing bridge columns under cyclic loading- part 2: analysis and comparison with theory[J]. ACI Structural Journal, 1999, 96(1): 57−67.

[7] Aditya Singh Rajput, Umesh Kumar Sharma. Seismic behavior of under confined square reinforced concrete columns[J]. Structures, 2018(13): 26−35.

[8] 蒋丽忠, 邵光强, 姜静静,等. 高速铁路圆端形实体桥墩抗震性能试验研究[J]. 土木工程学报, 2013(3): 86− 95. JIANG Lizhong, SHAO Guangqiang, JIANG Jingjing, et al. Experimental study on seismic performance of solid piers with round ended cross-section in high-speed railway[J]. China Civil Engineering Journal, 2013(3): 86−95.

[9] 鞠彦忠, 阎贵平, 刘林. 低配筋大比例尺圆端型桥墩抗震性能的试验研究[J]. 土木工程学报, 2003, 36(11): 65−69. JU Yanzhong, YAN Guiping, LIU Lin. Experimental study on seismic behaviors of large-scale RC round- ended piers with low reinforcement ratio[J]. China Civil Engineering Journal, 2003, 36(11): 65−69.

[10] 鞠彦忠, 阎贵平, 李永哲. 低配筋铁路桥墩抗震性能的试验研究[J]. 铁道学报, 2004, 26(5): 91−95. JU Yanzhong, YAN Guiping, LI Yongzhe. Experimental study on seismic behaviors of railway bridge piers with low reinforcement ratio[J]. Journal of the China Railway Society, 2004, 26(5): 91−95.

[11] 陈兴冲, 张永亮, 丁明波,等. 少筋混凝土重力式桥墩抗震设计方法研究[J]. 铁道工程学报, 2016(3): 76−80. CHEN Xingchong, ZHANG Yongliang, DING Mingbo, et al. Research on seismic design method for concrete gravity piers with low longitudinal reinforcement ratio[J]. Journal of Railway Engineering Society, 2016(3): 76−80.

[12] 陈兴冲, 张永亮, 丁明波,等. 罕遇地震下少筋混凝土桥墩最低配筋率研究[J]. 桥梁建设, 2016, 46(5): 24− 28. CHEN Xingchong, ZHANG Yongliang, DING Mingbo, et al. Study of minimum reinforcement ratios for concrete piers arranged with small amount of reinforcement under rare earthquake[J]. Bridge Construction, 2016, 45(5): 24− 28.

[13] JIA Junfeng, SONG Nianhua, XU Zigang, et al. Structural damage distribution induced by Wenchuan Earthquake on 12th May, 2008[J]. Earthquakes and Structures, 2015, 9(1): 93−109.

[14] NI S D, WANG W T, LI L. The April 14th, 2010 Yushu earthquake, a devastating earthquake with foreshocks[J]. Science in China Series D: Earth Sciences, 2010, 53(6): 791−793.

[15] WANG Wencai, LI Zuotang, DANG Hong, et al. Strong motion records and its characteristics in Jiuzhaigou Ms7.0Earthquake on August 8,2017[J]. China Earthquake Engineering Journal, 2017, 39(4): 652−656.

[16] Mander J B, Priestley M J N, Park R. The theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988, 114(8): 1804−1826.

[17] Dodd L L, Restrepo-Posada J I. Model of predicting cyclic behavior of reinforcing steel[J]. Journal of Structural Engineering, ASCE, 1995, 121(3): 433−445.

[18] Faria R, Pouca N V, Delgado R. Simulation of the cyclic behavior of R/C rectangular hollow section bridge piers via a detailed numerical model[J]. Journal of Earthquake Engineering, 2004, 8(5): 725−748.

[19] 司炳君, 孙治国, 艾庆华, 等. 钢筋混凝土桥墩滞回性能的有限元参数敏感性分析及模型改进[J]. 工程力学, 2009, 26(1): 174−180, 186. SI Bingjun, SUN Zhiguo, AI Qinghua, et al. Sensitive analysis and model modification for finite element analysis of R/C bridge piers under cyclic loading[J]. Engineering Mechanics, 2009, 26(1): 174−180, 186.

[20] Youssef M, Ghobarah A. Strength deterioration due to bond slip and concrete crushing in modeling of reinforced concrete members[J]. ACI Structural Journal, 1999, 96(6): 56−66

[21] Casanova A, Jason L, Davenne L. Bond slip model for the simulation of reinforced concrete structures[J]. Engineering Structures, 2012(39): 66−78.

[22] Han T S, Peter H F, Billington S L. Simulation of highly ductile fiber-reinforced cement-based composite components under cyclic loading[J]. ACI Structural Journal, 2003, 100(6): 749−757.

[23] 司炳君, 孙治国, 艾庆华. Solid65 单元在混凝土结构有限元分析中的应用[J]. 工业建筑, 2007, 37(1): 87−92. SI Bingjun, SUN Zhiguo, AI Qinghua. Application of Solid65 element in the finite element analysis of concrete structures[J]. Industrial Construction, 2007, 37(1): 87−92.

[24] 司炳君, 孙治国, 王东升,等. 利用ANSYS模拟桥墩滞回性能的建模方法研究[J]. 武汉理工大学学报, 2007, 29(6): 76−79. SI Bingjun, SUN Zhiguo, WANG Dongsheng, et al. Modeling methods on simulation of hysteretic behavior of bridge[J]. Journal of Wuhan University of Technology, 2007, 29(6): 76−79.

[25] Park, R. Evaluation of ductility of structures and structural assemblages from laboratory testing[J]. Bulletin of the New Zealand National Society for Earthquake Engineering, 1989, 22(3): 155−166.

[26] JGJ/T 101—2015, 建筑抗震试验规程[S]. JGJ/T 101—2015, Specification for seismic test of building[S].

Influence of longitudinal reinforcement ratio change in plastic hinge area on seismic performance of gravity bridge piers

LU Jinhua, CHEN Xingchong, DING Mingbo, ZHANG Xiyin, MA Huajun

(College of Civil Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China)

In view of the fact that the bending failure pier is only seriously damaged in the plastic hinge area at the bottom of the pier in earthquake, a method for the arrangement of longitudinal steel bars was proposed in this paper. That is, the number of longitudinal steel bars is increased only at the bottom of the pier (2 times the length of plastic hinge), while the number of steel bars in the rest of the pier remains unchanged. Five piers are designed, and the influence of reinforcement ratio change at the bottom of the pier on the seismic performance of piers is analyzed by ANSYS software. The results show that only increasing the longitudinal reinforcement ratio at the bottom of the pier can improve the bearing capacity of the pier, enhance the energy dissipation capacity of the pier and increase the displacement ductility of the pier. Compared with the traditional pier with the same reinforcement ratio in the whole section, the hysteretic curves of two piers have a serious “pinch” effect. By improving the longitudinal reinforcement ratio at the bottom of the pier with low reinforcement ratio, the pier can basically achieve the seismic performance of the pier with high reinforcement ratio in all sections.

gravity bridge pier; longitudinal reinforcement ratio; plastic hinge zone; seismic performance

U24

1672 − 7029(2020)09 − 2288 − 08