异质队列的分布式鲁棒解耦控制

高 锋 王晓彤

重庆大学汽车工程学院，重庆，400044

0 引言

日益增加的用车需求给交通带来了沉重的负担，导致交通堵塞等问题［1］。队列行驶能够提高交通效率和行驶安全性［2-3］。最早关于队列控制的研究可追溯到20世纪80年代末美国PATH项目［4］。此后，科研人员进一步对队列控制涉及的跟车策略［4-6］、通信拓扑的影响［7-9］、通信延迟［10-11］、均质和异质队列［12］等问题开展了广泛研究。为实现更小的跟车间距和队列稳定性等性能，先进的控制方法也得到了广泛应用，并实现了示范运行，如荷兰GCDC项目［13］、欧洲SARTRE项目［14］和日本Energy-ITS项目［15］等。

总结现有成果，队列控制主要有两种设计方法。一种是把所有车辆作为整体考虑。基于该方法，GUO等［16］考虑参数不确定性、通信延迟和跟踪性能设计了队列控制器，其缺点是控制器仅适用于固定长度和通信拓扑的队列。另一种采用分布式控制结构，将队列分解成多个子系统进行设计。STANKOVIC等［17］基于该方法设计了状态反馈次优控制器；HERMAN等［18］提出一种无需引导车信息，保证队列稳定的双向不对称控制器；ZHENG等［10］给出了不同拓扑条件下，状态反馈控制的渐进稳定条件。上述研究成果仅适用于均质队列，即所有节点动态特性一致，且未考虑模型误差的影响，而实际队列一般由不同车辆构成，且动力传动系统特性等难以精确建模，并随环境和工作状态变化。

此外，与一般的控制系统不同，为保证外部扰动引起的控制误差沿队列方向不被放大，队列稳定性也是需要考虑的重要性能。对于采用车载传感器或简单通信拓扑的队列，如跟随引导车［4-7］，其节点间耦合简单，队列稳定性已得到深入研究［19-20］。近年，DSRC（dedicated short range communication）、VANET（vehicular ad-hoc networks）等技术的发展，使得无线通信用于队列控制成为可能。但是无线通信会产生延迟和数据丢失，增大不确定性，同时车辆节点间的信息耦合也更加复杂［21］，已有队列稳定性理论不再适用，因此，基于解耦策略设计队列控制系统时，需综合考虑异质性和模型误差对稳定性、跟踪性能和队列稳定性的影响。

本文针对异质队列，提出了一种分布式鲁棒性能控制器的解耦设计方法。该方法采用乘性不确定性模型描述车辆及下位控制器构成的车辆节点的动态特性。在对通信矩阵对角化分解基础上，通过线性变换实现系统解耦，将其分解成范数有界的不确定部分和一个确定的对角系统。应用H∞理论对系统的鲁棒性能进行分析，并给出了队列稳定的充分条件。最后通过台架试验对比验证了所提方法的有效性。

1 问题描述

研究的队列如图1所示，由N+1辆车构成，可包含多种通信拓扑，如跟随型、引导车跟随型、双向型等［10］。

图1 异质队列Fig.1 Heterogeneous vehicular platoon

文中引入如下缩写和符号：RN×N为N×N阶实数矩阵；s为拉普拉斯算子；1N是元素全为1的向量，1N∈ RN；diag(A1,A2,…,AN)为由元素Ai构成的对角阵；I为单位阵；0为零矩阵；‖·‖2和‖·‖∞为信号的L2范数和导出范数（H∞范数）；σ(·)为奇异值(·)和-σ(·)表示最大和最小奇异值。

1.1 节点动力学和拓扑模型

队列采用分层结构，节点i由车辆纵向动力学和下层控制器构成下位系统的动态特性，采用乘性不确定性模型描述［22］：

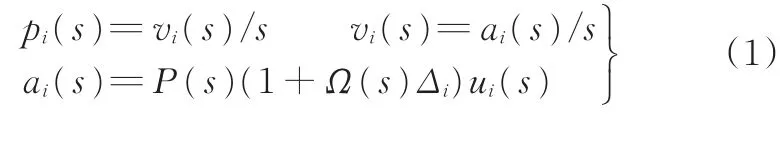
式中，pi为位移；vi为速度；ai为加速度；ui为期望加速度（控制输入；P(s)为标称模型；Ω(s)为权函数；Δi为归一化后的不确定性，满足‖Δi‖∞＜1，包含节点异质性和建模误差。

通信拓扑G采用图论法描述［8］：

其中，L是Laplacian矩阵，L=[lij]∈RN×N。若节点i与节点j通信，则lij=-1，否则lij=0。L的对角元素满足P是Pining矩阵，P=diag(g1,g2,…,gN)，用来描述引导车和跟随车之间的关系。若引导车和节点i通信，则gi=1，否则gi=0。与节点i通信的车辆构成的集合为

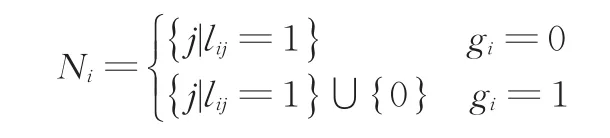
1.2 分布式控制器

队列采用恒定车距策略［3］，控制目标为

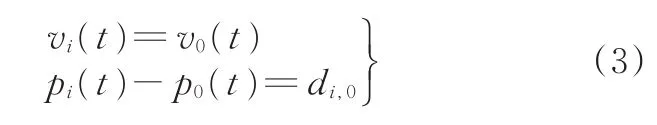
式中，di,0为期望车间距；p0(t)和v0(t)分别为引导车的位置和速度。

采用如下基于状态反馈的分布式控制器进行队列控制［18］：

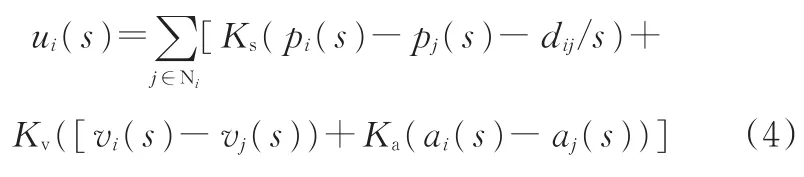
式中，Ks、Kv和 Ka为反馈系数。

为应用H∞理论，将式（1）转化为线性分式形式：

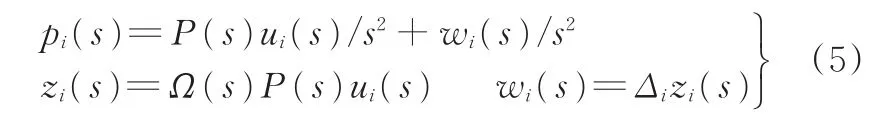
进一步考虑式（3），定义误差ei(s)=pi(s)-p0(s)-di,0/s和 K(s)=Ks+Kvs+Kas2，式（4）转化为

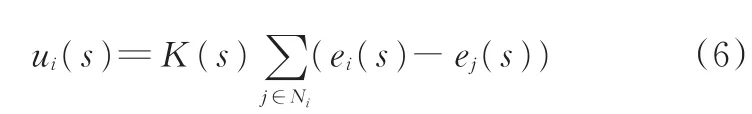
由式（2）、式（5）和式（6）得到队列控制系统模型：

Δ=diag(Δ1,Δ2,…,ΔN)满 足 ‖Δ‖∞＜ 1［23］。 式（7）将队列控制系统分解成确定和不确定部分，便于应用H∞理论设计分布式控制器。

2 控制系统解耦

原控制系统中，G使节点间产生耦合，增加了系统综合的复杂度。本节介绍如何通过线性变换实现系统解耦，原理如图2所示。

图2 队列控制系统解耦Fig.2 Decoupling of vehicular platoon

对于无定向通信拓扑具有如下特征值分解［10］：

式中，λi为G的特征值；X由特征向量构成，X∈RN。

式中，β为模型误差的上界。

将式（8）代入式（7）得到

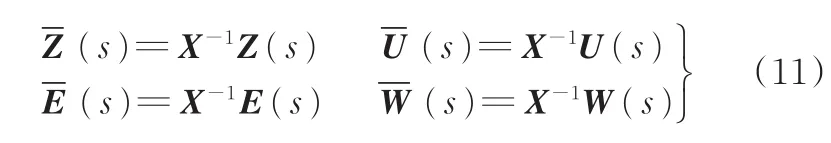
3 分布式H∞队列控制系统分析

根据式（3）的队列控制目标，设计控制器时需

要满足：①具有良好的鲁棒稳定性；②具有良好的抗扰动能力性能；③具有队列稳定性。

3.1 鲁棒稳定性

为方便控制器设计，由式（9）和式（11）得到新的队列系统方程如下：

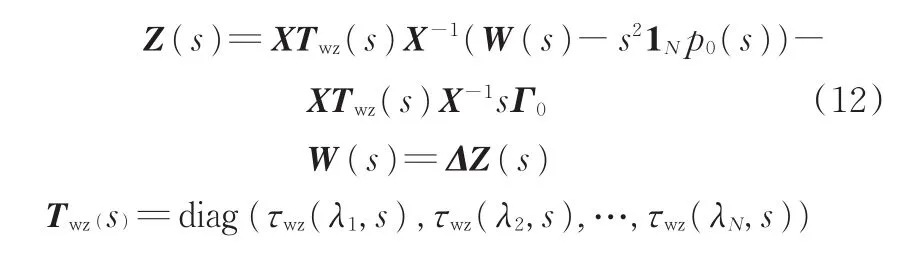
Twz(s)的元素为

根据小增益定理知，式（7）鲁棒稳定当且仅当下式成立：

由于‖Δ‖∞≤β，式（14）成立等价于

进一步，由1Na0(s)=[a0(s)a0(s)…a0(s)]T（a0(s)为引导车加速度）和sΓ0=s[d10d20… dN0]T可得

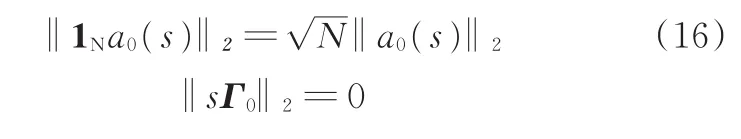
将式（14）～式（16）代入式（12）得

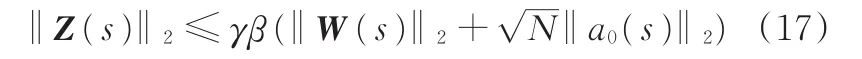
由‖W(s)‖2≤ ‖Z(s)‖2和式（17）可知，由模型误差引起的扰动满足：综合上述分析可知，当分布式控制器使得各子系统满足式（15）时，队列鲁棒稳定。

3.2 鲁棒性能分析

为分析队列跟踪性能，由式（9）和式（11）得到

类似于鲁棒稳定性的分析，由式（19）可得

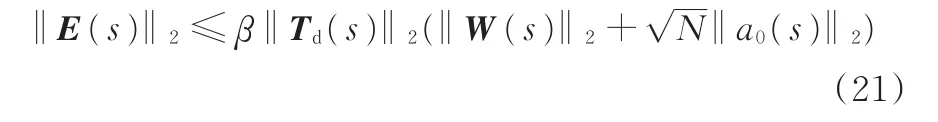
若分布式控制器K(s)使得各子系统同时满足式（18）和下式

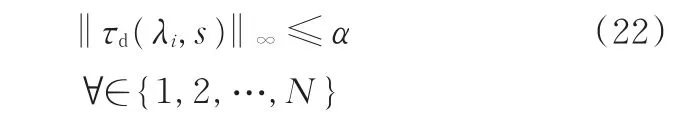
则此时跟踪误差满足如下鲁棒性能要求：

3.3 队列稳定性

采用分布式状态反馈控制策略时，引导车信息是保证队列稳定性的必要条件［9］。因此，在跟随车均能与引导车通信的条件下（P=I）对队列稳定性进行分析。由式（2）可以得到

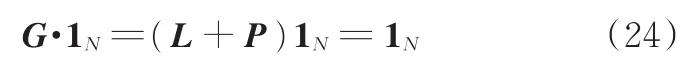
可知1是G的特征值，对应特征向量为1N。为分析解耦特性，定义如下特征值分解：

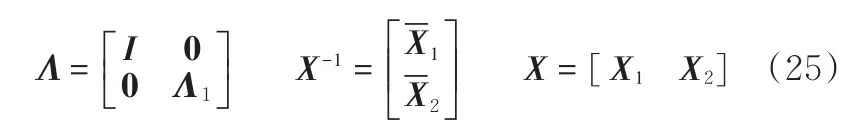
式中，Λ1为由λi构成的对角阵，λi≠ 1。

由X-1X=XX-1=I得到

进一步，由式（24）和式（25）可得

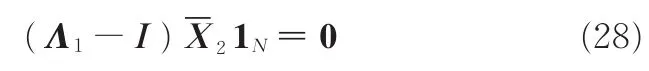
因 Λ1由 λi构成，当且仅当·1N=0时，式（28）成立。

根据上述分解，由式（25）和式（26）将式（7）分解为

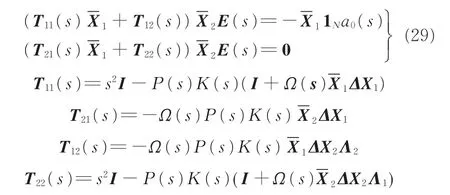
式（29）中第二个等式成立当且仅当

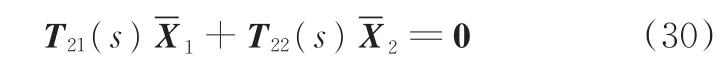
进一步，由式（26）和式（30）可得

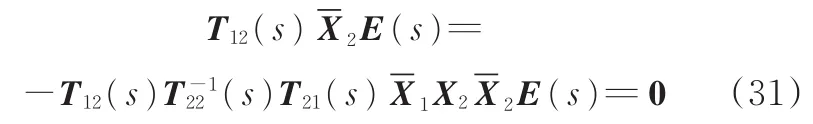
将式（31）代入式（29）第一个等式，结合式（26），有

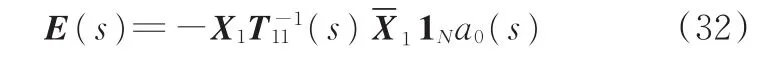
两边同乘X1和考虑得到

将式（34）代入式（32）得到队列等效解耦形式

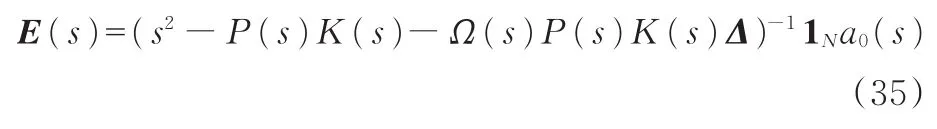
可以看出，引导车信息能够使各子系统实现解耦：

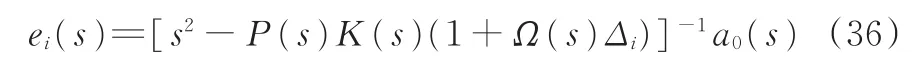
根据文献［24］，当K(s)可镇定P(s)[1+ Ω (s)Δi]时，队列稳定，且控制误差满足‖ei(s)‖2≤

4 台架试验验证和分析

本节通过图3所示的台架试验验证提出的解耦鲁棒控制方法的有效性。车辆模型运行在NI的PXI实时仿真平台上，控制算法运行在i.MX6开发板上，节点间的无线通信通过该开发板的wifi通信模拟，实时仿真平台和开发板之间通过CAN总线传输信号。

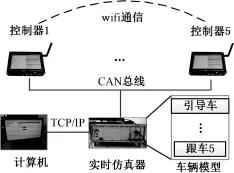
图3 台架测试平台Fig.3 Test bench

实验时，队列每个节点模型由车辆逆模型和纵向动力学模型组成，采用分层控制结构，将队列控制器产生的期望加速度输入到下位控制器，计算得到节气门/制动指令［22-24］。队列的期望跟车距离为20 m。引导车初始速度为20 m/s，10 s处加速，其加速度曲线如图4所示。

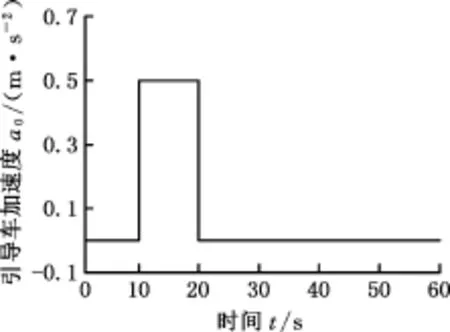
图4 引导车加速度Fig.4 Acceleration profile of leader

4.1 鲁棒性能

测试队列包括6辆车（含引导车），采用双向通信拓扑［10］，此时 G 的特征值分别为 0.08、0.69、1.72、2.83和3.68。将测试结果与非鲁棒控制器K(s)=-s2-4s-0.4进行对比，无模型误差时的距离误差如图5所示。引导车停止加速后约20 s时，距离误差收敛至零且无明显振荡。

图5 无模型误差的距离误差Fig.5 Distance tracking error when no model errors

无模型误差时系统虽然稳定，但由式（13）可知，当 Δi≠0 时，max(||τwz(λi,s)||∞)=1.1＞ 1，队列可能不稳定。考虑车辆质量对车辆特性影响较大，将其作为不确定因素。当车辆质量随机产生（1.No.1，2.No.2，3.No.3，4.No.4，5.No.5，图6a所示）时，非鲁棒控制器产生振荡剧烈（图6b），此时设计的鲁棒控制器K(s)=-0.6s2-2.7s-0.5，max(||τwz(λi,s)||∞)=0.86＜ 1。距离误差如图6c所示，距离误差最大值约13 m。引导车停止加速后，约50 s收敛至零且无明显振荡。与非鲁棒控制器相比，队列的鲁棒稳定性能得到显著改善。但由于提高鲁棒稳定性需要牺牲其他性能［24］，所以收敛时间和最大误差有所增加。

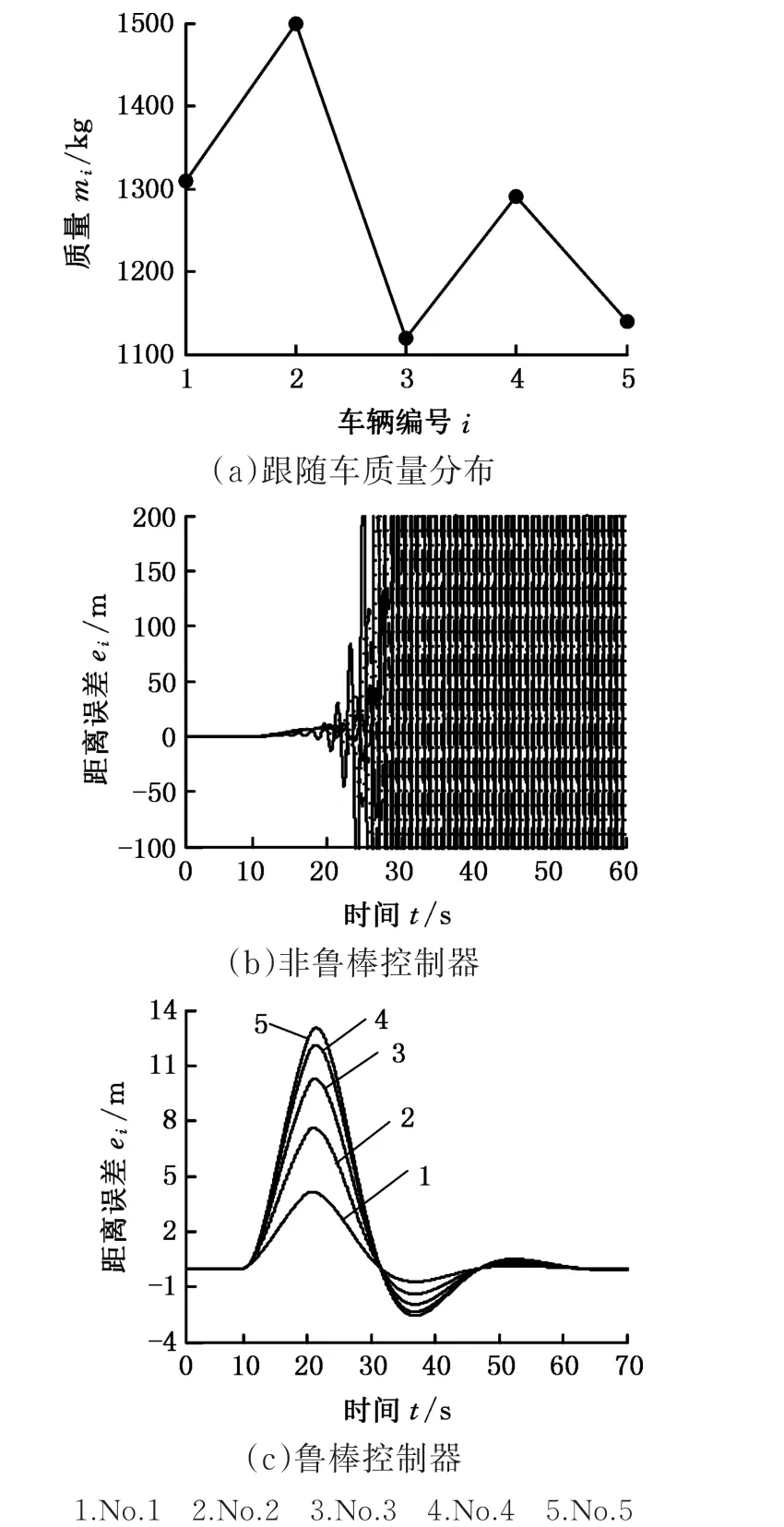
图6 节点模型存在误差的测试结果Fig.6 Test results with model errors

4.2 异质队列稳定性

本节对比双向通信（BD）和双向引导车通信（BDL）两种通信拓扑［10］。跟踪性能由最大距离误差衡量，结果如图7所示。虽然双向通信拓扑下系统稳定，但最大误差随队列长度线性增大，队列不稳定。而采用双向引导车通信拓扑，距离误差不随队列长度增大而增大，此时队列稳定，与前文的理论分析一致。

图7 最大距离跟踪误差与队列长度的关系Fig.7 Maximum distance tracking error vs.platoon length

5 结论

（1）对于分布式队列控制系统，节点动力学异质性和建模误差可能引起系统性能衰减，进行控制器设计时，需要考虑鲁棒稳定性和跟踪性能。

（2）本文提出的分布式鲁棒解耦控制器设计方法能够保证队列的鲁棒稳定性，跟踪性能和队列稳定性。

（3）与跟随车信息相比，引导车信息对提高控制性能更加重要，且能够实现通信连接引起的动力学特性耦合的解耦。