融合车、路、人信息的电动汽车续驶里程估算
2018-08-17高建平高小杰郗建国
高建平 高小杰 郗建国
1.河南科技大学车辆与交通工程学院,洛阳,471003
2.河南科技大学机械装备先进制造河南省协同创新中心,洛阳,471003
0 引言
续驶里程是人们购买电动汽车时重点考虑的问题之一。续驶里程短及目前充电桩等基础设施的不完善,严重影响了人们对电动汽车的购买动力。针对这一问题,除了发展动力电池技术之外,还需要更加准确实时地预测续驶里程等参数[1-2],以提升用户感受,加快电动汽车的推广应用。目前针对实际不同行驶工况下电动汽车剩余续驶里程及实时估计的研究较少,特别是关于驾驶风格的不同对续驶里程估算的影响,以及对估算结果的进一步优化的研究文献更是鲜见。尹安东等[3]通过工况识别,实现了对当前车辆能耗的预测,完成车辆续驶里程估算,但其研究中未考虑驾驶员信息;刘光明等[4]在建立电池荷电状态的实时估算模型及电池温度预测模型的基础上,进一步建立了电池剩余可用能量预测模型,实现了对车辆续驶里程的预测,但其研究也未考虑驾驶员因素;ZHANG等[5]在里程估计算法中直接应用剩余能量预测值,其方法基于Telematics System提供道路信息和汽车状态信息,但未包含驾驶员信息;OLIVA[6]等应用粒子滤波方法对SOC和续驶里程值进行估计,未专门考虑行驶工况及驾驶员因素对续驶里程估算的影响;SIY等[7]和PANDIT等[8]通过计算当前时间段的能耗来预测下一时间段能耗,再根据电池剩余能量来预测剩余续驶里程,此方法估算结果比较保守,未在能耗预测过程中考虑驾驶员因素,并且在工况急剧变化情况下存在估算不稳定的问题。
笔者通过采集大量的郑州市纯电动公交车实际行驶工况数据,选出典型郑州市行驶工况运动学片段作为学习矢量量化(learning vector quantization,LVQ)神经网络学习的典型样本,在此基础上建立主成分分析(principal component analysis,PCA)与LVQ神经网络相结合的行驶工况识别模型,并在工况识别基础上建立驾驶风格识别模型,实现对车辆能耗的准确预测,进而实现对车辆剩余续驶里程的估算。针对由于工况及电池可用能量变化时估算结果频繁波动变化的情况,通过卡尔曼滤波(Kalman filter,KF)对输出剩余续驶里程进行了优化,并通过实际工况进行续驶里程仿真分析及半实物测试验证。
1 典型工况训练片段选取
1.1 汽车行驶工况数据采集
将车载终端设备(图1)安装于试验公交车辆,行驶数据由车载终端设备实时采集,采样频率为1 Hz[9]。通过通用分组无线服务技术网络,将采集到的车辆运行过程中的相关信息传送到车辆远程管理服务平台,从中国汽车工况信息化系统查询并下载数据。

图1 车载终端设备Fig.1 Vehicle terminal equipment
1.2 运动学片段特征参数提取
行驶工况可以看作是众多运动学片段[6]的组成。参考文献[10-13],选取可以全面表征运动学片段的速度、加速度、时间、距离以及加减速等特征的12个特征参数对其进行描述,12个特征参数分别为:平均运行距离s,m;平均速度vavg,m/s;最大速度vmax,m/s;运行时长tall,s;怠速时间till,s;加速时间tacc,s;减速时间tdec,s;匀速时间tcon,s;最大加速度 amax,m/s2;最小加速度 amin,m/s2;减速段平均加速度aavg-,m/s2;加速段平均加速度aavg+,m/s2。
将实际采集的300多万组行驶工况数据通过MATLAB软件编程进行处理,得到20 182个有效运动学片段,进而编程处理得到一个样本数量(行)×特征值(列)矩阵,如表1所示。
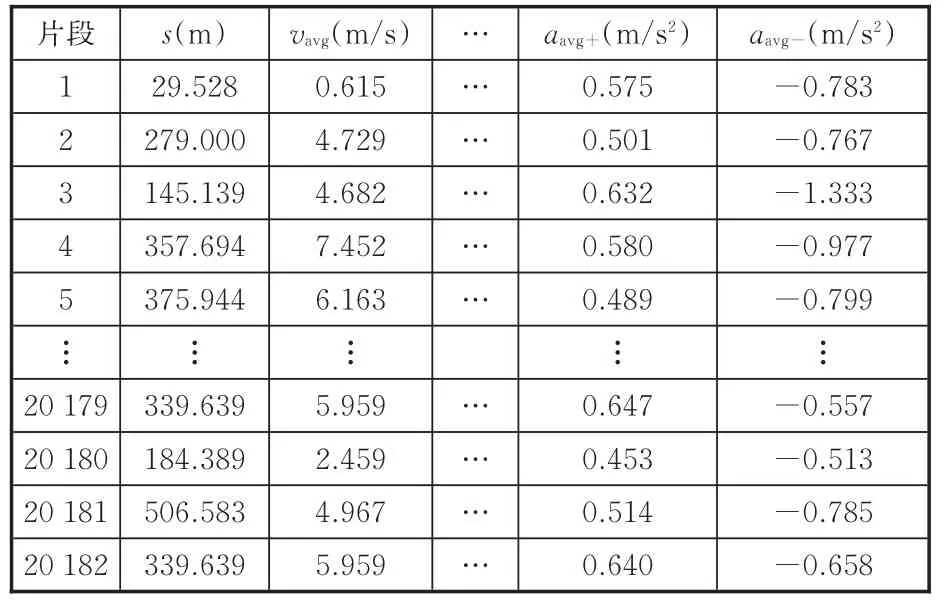
表1 运动学片段特征参数Tab.1 Characteristic parameters of kinematic segments
1.3 主成分分析
主成分分析[10]可以通过消除变量之间的相关性,最终得到几个综合变量来反映所研究问题的大部分信息,该分析方法不仅可以反映事物的本质,而且可以简化后续的计算。
针对上述矩阵进行主成分分析。得到的12个主成分的特征值、贡献率和累积贡献率见表2,各成分使用Mi(i=1,2,…,12)表示,前4个主成分的累计贡献率已经达到83.767%,所包含的特征参数信息能够用于表征整个运动学片段,故前4个主成分用于聚类分析。
1.4 模糊C均值聚类
1.4.1 最佳聚类数的选取
利用模糊C均值聚类分析对20 182个运动学片段分别进行2~20类聚类。通过描述类间离差矩阵分离度、类内离差矩阵紧密度的CH(Calinski-Harabasz)指标(CH值)对划分为2~20类工况进行评价,从而确定最佳聚类。CH值表达式如下:

表2 各个成分特征值、贡献率、累积贡献率Tab.2 Eigen values,contribution rates and cumulativecontribution rates of each component

式中,n为行驶工况聚类数目;k为当前所处工况类型;trW(k)为相同类工况所有片段离差矩阵W(k)的迹;trB(k)为不同类行驶工况之间离差矩阵B(k)的迹。

图2 不同聚类数CH指标Fig.2 CH index of different cluster number
CH值越大表示聚类所得的相同类的行驶工况之间的距离和越小,不同类行驶工况之间的距离和越大,聚类数选取越佳,由图2可知,将郑州市行驶工况分成3类为最佳分类数。
1.4.2 模糊C均值聚类分析
表3所示为通过模糊C均值聚类(3类)后各类工况综合特征值及全部数据综合工况特征值,其中,Pi为怠速比例,Pa为加速比例,Pd为减速比例,Pc为匀速比例。第1类怠速比例高达53.201%,平均每个片段运行时间26.450 s,平均速度仅为6.386 km/h,说明车辆在此工况行驶时,车流量被严重限制,代表车辆处于城市闹市区工况;第2类怠速比例30.400%,平均每个片段运行时间42.673 s,平均速度15.941 km/h,代表车辆处于城市生活区工况;第3类怠速比例仅13.110%,平均每个片段运行时间98.777 s,且平均速度20.542 km/h,说明在该道路行驶时,车流量较小、较畅通,代表车辆在城市郊区工况。
1.5 典型工况片段选取
计算各类样本中的各个片段与该类总样本数据的相关系数ρXY,并从3类行驶工况中分别选取与该类所有数据相关系数大的片段,用于LVQ神经网络训练。ρXY的表达式为

表3 各类数据综合特征值Tab.3 Overall characteristic parameters of each category
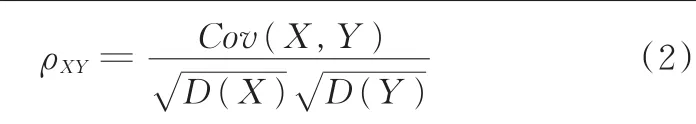
式中,X为各个工况片段特征参数数据;Y为总体样本工况特征参数数据;Cov(X,Y)为X、Y的协方差;D(X)、D(Y)分别为X、Y的方差。
2 基于PCA-LVQ神经网络的汽车行驶工况识别
车辆在实际使用过程中,由于行驶工况经常发生变化,而不同工况对应的能耗有一定的差别,因此能够实时准确地识别工况类别,对剩余续驶里程的更准确估计起着重要作用。
为了更加准确地识别汽车行驶过程中的工况类别,应采用较多的行驶工况特征参数,但是由于工况特征参数之间有一定的相关性,且特征参数的量纲不尽相同,因此直接利用工况特征参数对车辆行驶工况进行识别,会在很大程度上影响识别准确性。通过对全面、系统反映运动学片段的众多特征变量作主成分分析,并将其作为LVQ神经网络识别模型输入,不仅能大大缩短网络训练时间,简化计算,而且可消除通过特定特征参数进行工况识别时量纲的影响,提高了LVQ网络模型识别的准确率。
基于主成分分析(PCA)和LVQ神经网络的行驶工况识别流程图见图3,主要包括两部分:①离线LVQ样本训练部分。利用选取的代表性运动学片段对其主成分进行提取,并进行LVQ神经网络训练。②在线LVQ工况识别部分。对采集的汽车行驶过程中的工况数据进行特征参数提取及主成分提取,将其作为LVQ神经网络识别模型的输入层,进而输出该片段所属的行驶工况类型,并进行实时识别及更新。考虑到识别周期对识别效果的影响,结合实时处理能力及所采集实际行驶工况数据的片段长度,选取120 s为识别周期[14]。

图3 工况识别流程图Fig.3 Flow chart of working condition identification
2.1 LVQ神经网络
LVQ神经网络[15]结构如图4所示,由输入、竞争和线性输出3层神经元组成。图中,P为R维的输入模式;S(1)为竞争层神经元个数;W(1.1)I为输入层与竞争层之间的连接权系数矩阵;n(1)为竞争层神经元的输入;a(1)为竞争层神经元的输出;W(2.1)L为竞争层与线性输出层之间的连接权系数矩阵;n(2)为线性输出层神经元的输入;a(2)为线性输出层神经元的输出;ndist为计算输入层向量与竞争层向量之间的欧氏距离;compet(·)为竞争层传递函数;purelin(·)为线性函数。

图4 LVQ神经网络结构Fig.4 Architecture of LVQ neural network
2.2 工况识别样本训练
对选取的各类典型工况训练片段进行特征参数提取,进而提取主成分,作为LVQ神经网络训练样本数据,用于LVQ神经网络的行驶工况识别模型训练,训练过程如图5所示。根据训练样本的主成分及所属类别不断调整竞争层权值,训练结束之后,将最终竞争层权值应用于行驶工况识别。
2.3 工况识别模型验证

图5 样本训练过程Fig.5 Sample training process
对采集的行驶工况数据的20 182个有效片段(包括6 294个第1类工况片段、8 325个第2类工况片段、5 563个第3类工况片段)进行各个片段特征参数提取,进而提取主成分并作为测试集,结果如表4所示。由表4知,第1类和第3类识别正确率较高,均超过90%;第2类相对较低,由于第2类工况处于第1、3类之间,有一部分工况片段与第1、3类相似度高,故综合正确率为90.17%。由此可知,基于PCA-LVQ的行驶工况识别法可以更加准确地实时识别出当前所处行驶工况。

表4 不同工况类型识别结果Tab.4 Recognition accuracy of different driving cycle
3 驾驶员驾驶风格识别
通常将驾驶员的驾驶风格划分为3类:经济型、一般型、动力型,不同驾驶风格的驾驶员踩加速踏板、制动踏板的幅度及速度不同。但由于驾驶员对加速踏板、制动踏板的使用会受到车辆实际行驶工况的影响,因此驾驶风格的识别需要在工况识别的基础上进行才更加合理。
驾驶员是“车-路-人”系统中的重要环节,驾驶风格又是驾驶员在道路上的动态行为,相同的公交线路,相似的行驶工况下,同型号电动汽车不同驾驶风格的能耗差异往往较大[16]。因此通过识别当前行驶工况,并在此基础上对驾驶风格进行识别,才能更加准确地得到纯电动汽车行驶过程中的能量消耗。
平均加速度和加速度标准差大小可以反映驾驶员在驾驶车辆过程中对动力性的要求及加速度的分散程度,本研究联合采用平均加速度和加速度标准差参数对驾驶风格进行模糊识别。
加速度平均值

式中,n为采样次数;ai为加速度第i次采样值,m/s2。标准差

采用K均值聚类的方法,联合采用平均加速度与加速度标准差参数对20 182个运动学片段进行3类聚类分析。聚类得到3类聚类中心以(aˉ,s(a))表示为(0.240,1.742)、(0.310,2.546)、(0.430,3.579),分别作为经济型、一般型、动力型驾驶风格工况片段的聚类中心。通过式(2)相关系数计算公式选取各类典型驾驶风格片段用于模糊控制器参数的确定。
模糊控制主要借鉴专家的经验来选择控制器的结构和参数,但仅仅靠专家的经验很难得到满意的效果。本文模糊控制器的模糊规则比较简单,因此需要对隶属度函数进行优化。采用典型驾驶风格片段利用遗传算法优化模糊控制器隶属度函数,得到平均加速度、加速度标准差隶属度函数(图6)。驾驶风格推理规则表见表5。

图6 平均加速度及加速度标准差隶属度函数Fig.6 Membership function of average acceleration and standard deviation of acceleration

表5 驾驶风格推理规则表Tab.5 Inference rule table of driving style
4 动力电池剩余可用能量估计
电池作为复杂的电化学系统,在不同状态、不同工况下的可用能量均不相同[17]。本文选取的某公司8 m纯电动客车采用标称电压为518.4 V的磷酸铁锂LiFePO4动力电池组,其额定容量为172 A·h。根据锂电池基本特性,在综合考虑三种简化电化学模型基础上,建立了锂电池电化学复合模型[18]。该模型不仅考虑了温度的影响,而且将充放电倍率及充放电方向考虑在内,能准确反映锂电池的动态特性。其数学表达式如下:
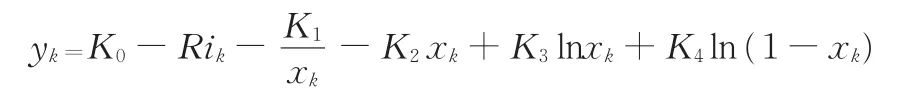
式中,yk为电池工作电压;ik为k时刻电流值;R为电池内阻,充电时R=RC(ik为负),放电时R=Rd(ik为正);xk为k时刻的瞬时荷电状态;K0、R、K1、K2、K3、K4为复合电化学模型匹配系数。
对电池荷电状态(SOC)值作如下定义:

对式(3)进行离散化处理得

式中,xk为k时刻SOC值;ik-1为k-1时刻电流值;Δt为时间间隔。
由此,得到锂电池的状态空间模型。状态方程为

观测方程为
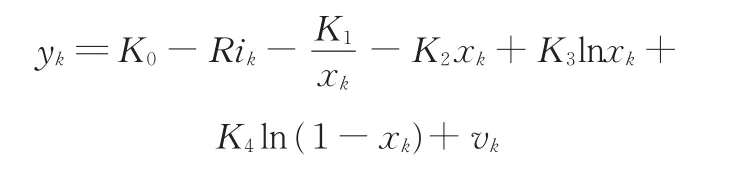
式中,wk、vk分别为均值为0的高斯白噪声。
利用磷酸铁锂离子动力电池组试验获得电流、电压和真实SOC值,采用自适应模拟退火(ASA)算法对电化学复合模型参数进行辨识,得到最优充放电内阻及模型匹配参数。参数辨识结果如表6所示。

表6 参数辨识表Tab.6 Parameter identification table
对电动汽车行驶过程来说,电池的剩余放电能量ERDE是指以某一工况行驶时,从当前时刻直至电池放电截止这一过程中,电池累计能提供的能量。电池剩余能量值

式中,ERDE(t)为当前时刻电池剩余能量值;为允许的放电截止SOC值(本文取0);Qst为电池标准容量;Ut为放电平均电压。
5 融合车、路、人信息电动汽车续驶里程估算
5.1 估算方法
本文在确定的汽车本身状态下,通过实时识别纯电动汽车行驶过程中不同行驶工况、驾驶员驾驶风格,从而更加准确地得到行驶过程中的能耗,并结合磷酸铁锂LiFePO4电池剩余可用能量,进而实现剩余续驶里程的实时预测。
为了更好地反映车辆行驶能耗的最新变化,采用调整当前行驶工况的单位里程能耗与历史单位里程能耗的权值的方法,即当前时刻路段工况类型平均能耗采用较大的权重,而历史单位里程能耗采用较小的权重,计算公式如下:

式中,lavg为平均单位里程能耗;whis为历史单位里程能耗的权重;lhis为历史单位里程能耗;wcur为当前单位里程能耗的权重;lcur为当前单位里程能耗。
融合车、路、人信息的电动汽车剩余续驶里程估算方法如图7所示。

图7 融合车、路、人信息的电动汽车续驶里程估算Fig.7 Driving range estimation for electric vehicles through vehicles,roads,and human information fusion
首先将采集的郑州市工况数据聚类成3类工况,分别输入整车模型,计算得到各类工况的单位里程能耗。通过获取行驶过程中最近120 s的一个片段,并对该片段进行工况识别、驾驶风格识别,计算行驶过程所消耗的能耗,累加得出总能耗。通过速度积分得到车辆行驶里程数,进而计算历史单位里程能耗,并结合当前工况单位里程能耗,计算能动态反映车辆工况最新变化的单位里程能耗,并结合动力电池剩余可用能量实时计算得到剩余续驶里程的实时预测。
5.2 估算实例
5.2.1 各类工况单位里程平均能耗
选取某公司8 m纯电动客车为研究对象,图8为该电动客车整车动力系统结构简图。表7为所示主要技术参数,整车模型在前向仿真软件AVLCRUISE中搭建,并通过AVL-CRUISE里的外部电池接口将在MATLAB/Simulink里建立的动力电池电化学复合模型链接到AVL-CRUISE中。通过将采集到的3类行驶工况分别输入到整车模型,仿真计算出各类行驶工况的单位里程平均能耗。

图8 系统结构简图Fig.8 Schematic diagram of system

表7 整车技术参数Tab.7 Vehicle technical parameters
数据采集过程中,会由于设备传输问题及驾驶员操作失误,导致所采集的实验车工况数据有噪点,从而影响到电机的工作状态,导致仿真的电耗结果与实际值偏差较大,因此在仿真之前需对郑州工况进行平滑处理,所采用平滑曲线滤波器定义为[7]

式中,K(x)为t时刻前后速度的权值。
K(x)函数如下:

图9为随机选取的一段工况数据滤波前后的时间(t)-速度(v)曲线对比图。

图9 工况数据滤波前后对比图Fig.9 Comparison chart of condition data before and after filtering
通过MATLAB/Simulink与AVL-CRUISE联合仿真得出8 m纯电动客车在第1、2、3类车辆行驶工况单位里程平均能耗分别为5 076 W·h/km、6 025 W·h/km、4 620 W·h/km。
5.2.2 续驶里程估算
由式(4)可得动态反映车辆工况最新变化的单位里程能耗lavg。
已消耗总能量
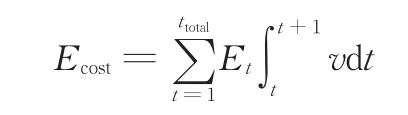
历史单位里程能耗
lhis=Ecost/S
剩余续驶里程
Sres=ERDElavg
式中,Ecost为纯电动客车历史工况总消耗;Et为当前汽车单位里程能耗;ttotal为行驶总时间;S为纯电动客车已行驶里程;ERDE(t)为当前时刻电池剩余能量值。
6 仿真分析及半实物测试验证
6.1 仿真分析
随机选取一部分车载终端设备采集的实车行驶工况数据作为测试数据,利用MATLAB/Simulink与AVL-CRUISE联合仿真,从而验证所采用的融合车、路、人信息的电动汽车续驶里程估算方法的准确性和可行性。
分别采用工况识别法和工况识别与驾驶风格识别相结合的方法得到估算值,估算值与实际值的比较结果如图10所示。由图10可知两种估算方法在估算初始阶段波动较大,由于历史工况数据较少,且随着工况的变化,单位里程能耗变化较大,导致估算结果随之变化较大。但随着历史数据的逐渐积累,单位里程能耗逐渐收敛于一个值(图11),从而使得两种方法估计的剩余续驶里程波动也随之变小。两种估算方法所得的剩余里程估算与实际值之间的误差对比如表8所示。由表8比较可知,采用融合车、路、人信息的估算方法是可行的,且相比工况识别法精度更高。
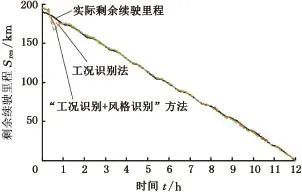
图10 两种估算方法对比Fig.10 Comparison of two estimation methods
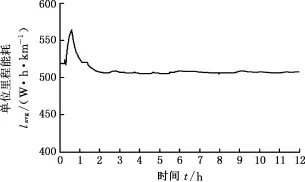
图11 单位行驶里程能耗Fig.11 Energy consumption per unit mileage

表8 两种估算方法误差对比Tab.8 Error comparison of two estimation methods
均方根误差(REMD)被广泛应用于不同数据之间偏差的对比,尤其是基于模型估计的预测值与真实值之间的对比。为了进一步验证采用融合车、路、人信息的纯电动客车续驶里程估算方法的有效性,本文以均方根误差作为评价指标,其计算式如下:

式中,v(i)为第i个剩余续驶里程预测值;vz(i)为对应时刻剩余里程真实值;n为总预测次数。
工况识别法和“工况识别+风格识别”方法对剩余里程估算结果的均方根误差分别为2.609 km和1.536 km。可以看出,采用的融合车、路、人信息的“工况识别+驾驶风格识别”方法与工况识别法相比,均方根误差降低了41.13%。
为避免由于工况及驾驶风格改变时,仪表上实时显示的剩余续驶里程频繁跳变,对采用融合车、路、人信息的估算结果采用卡尔曼滤波(KF)方法再次优化处理,优化后剩余里程显示过渡更加平滑,从而避免驾驶员产生焦虑情绪。图12为KF优化前后剩余续驶里程曲线对比及局部放大图。经过KF优化后绝对误差平均值为0.801 km,平均误差为1.120%,均方根误差为1.308 km,可知经过KF优化后各种误差进一步减小,估算精度得到提高。
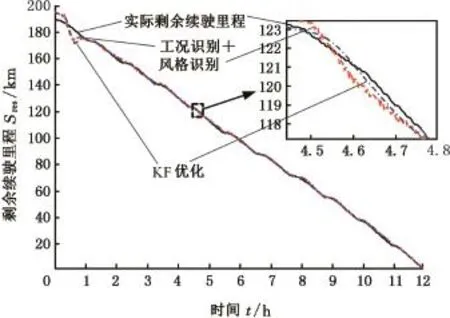
图12 KF优化前后剩余续驶里程曲线对比Fig.12 Contrast before and after Kalman optimization
6.2 半实物测试验证
引入半实物仿真平台进行进一步验证。平台硬件系统主要由dSPACE、CANoe及驾驶员模拟器组成,软件系统主要包括AVL-CRUISE、MATLAB及dSPACE自带的数据监控软件ControlDesk。控制对象采用dSPACE的I/O接口连接,试验采用两路ADC模数转换通道分别采集真实驾驶员的油门踏板和制动踏板信号,一路局域网通道实现数据的接收与发送。CANoe作为CAN通信控制器,可真实模拟实车数据间的信号传输,并且由真实驾驶员跟随目标车速踩下油门和制动踏板,使该仿真试验更接近于真实实车试验,测试方案如图13所示。
半实物测试表明:采用融合车、路、人信息的纯电动客车续驶里程的估算方法,平均误差2.457%,绝对误差平均值1.392 km,均方根误差2.180 km,各类误差较小,进一步验证了融合车、路、人信息的电动汽车剩余续驶里程方法的准确性及可行性。
7 结论

图13 半实物仿真试验方案Fig.13 Hardware in the loop simulation test scheme
(1)通过主成分分析和聚类分析法,并利用CH指标,确定汽车行驶工况的最佳聚类数,并选出基于大数据的、符合郑州市交通特点的公交车各类实际代表性行驶工况片段,用于工况识别模型的训练。
(2)建立基于主成分分析和LVQ神经网络的行驶工况识别模型,综合识别正确率达90.17%,并在工况识别的基础上,通过模糊控制的方法对驾驶风格进行识别,增加驾驶员信息,进而进行融合车、路、人信息的电动汽车剩余续驶里程仿真估算,并利用卡尔曼滤波对续驶里程估算结果作进一步优化,提高了剩余里程估算精度。
(3)采用实车采集的工况数据对纯电动客车估算方法仿真分析对比验证,结果表明融合车、路、人信息的电动汽车剩余续驶里程估算方法误差较小,可有效提高估算精度;半实物测试结果表明,所采用的估算方法是可行的。
