基于粒子群优化支持向量机算法的行驶工况识别及应用
2018-08-17仇多洋李一鸣刘炳姣
石 琴 仇多洋 吴 冰 李一鸣 刘炳姣
合肥工业大学汽车与交通工程学院,合肥,230009
0 引言
在新能源汽车的研发过程中,行驶工况识别得到越来越广泛的应用。对于混合动力汽车,在制定的能量管理策略中,如果能够识别当前行驶工况的特点,实时调整能量控制参数值,实现不同动力源之间功率分配最优,则可进一步提高整车燃油经济性[1-7]。而对于纯电动汽车,准确识别出实时行驶工况类型,获得相应类型工况下电耗水平,有助于提高纯电动汽车剩余续驶里程估算的准确性[8-9]。
当前行驶工况识别方法大致可分为三类:①采用神经网络算法进行识别。WANG等[10]利用数理统计方法筛选出识别参数,并用学习向量量化(learning vector quantization,LVQ)神经网络算法进行行驶工况识别;JEON等[11]定义一系列特征参数来描述行驶工况,采用Hamming网络进行行驶工况识别;周楠等[12]应用竞争型神经网络算法确定实时行驶工况隶属的标准工况类型。②采用模糊控制器进行识别。田毅等[13]采用遗传算法优化的模糊控制器对广州和上海主干道行驶工况进行识别。③利用聚类理论进行识别。RAVEY等[14]将平均车速、停车次数、停车时间、加速度和减速度5个参数及其权重的乘积作为聚类参数,利用动态聚类理论判断实际行驶工况所属的标准工况类别;秦大同等[7]通过计算待识别工况与标准工况特征参数的欧几里得距离确认行驶工况所属类型;詹森等[3]利用遗传算法优化的K均值聚类算法进行行驶工况识别。
上述研究中,采用神经网络算法识别行驶工况时,训练过程中隐含层神经元个数存在不确定性,导致识别结果存在较大差异,很难得到最优识别模型;采用模糊控制器进行行驶工况识别时,隶属度函数大多根据经验选择,只有反复调试才可以提高识别精度;采用聚类理论进行行驶工况识别时,聚类中心初始值对识别结果影响较大,容易陷入局部最优解的情况,同时对输入参数的个数比较敏感。
支持向量机(support vector machine,SVM)是根据统计学习理论的VC理论和结构风险最小化原则提出的一种针对有限样本情况的机器学习方法[15],大大简化了通常的分类和回归问题,且具有较好的鲁棒性。SVM作为有监督的学习理论,没有聚类理论中初始聚类中心的设置问题,同时避免了人工神经网络等理论的网络结构选择、过学习和欠学习等问题,可广泛用于模式识别。
为了提高SVM算法识别精度,本文将粒子群优化(particle swarm optimization,PSO)算法和SVM算法相结合,建立最优的行驶工况识别模型,分析了识别周期和更新周期对实时在线识别精度的影响;将行驶工况识别技术应用在插电式混合动力汽车的能量管理策略中,验证了行驶工况识别有助于整车实时最优控制,并提高了混合动力的汽车燃油经济性。
1 理论基础
1.1 支持向量机识别算法
SVM算法基本思想是:通过非线性映射将低维空间的输入数据映射到高维的特征空间,使其成为线性可分,在高维空间求解最优判别函数,确定分类边界。
已知线性可分情况下训练样本集:{(xi,yi)}其中,xi∈Rn,yi∈{-1,+1}(i=1,2,…,l)。利用最优分类超平面ωxi+b=0对样本进行分类,离最优分类超平面最近的两类样本称之为支持向量。支持向量与最优超平面之间的距离之和为根据结构风险最小化原则,应使该距离之和最大,因此求解最优超平面的问题转化为下述优化问题:

式中,ω为最优分类超平面的法向量;b为阈值,b∈R。
针对训练样本集大多数情况是线性不可分的,SVM引入非负松弛因子ξi,同时加入惩罚系数C。通过核函数进行非线性映射后,将上述目标函数变化为

使用Lagrange乘子法求解上述最小值问题。建立Lagrange函数如下:

式中,αi为Lagrange乘子,是辅助非负变量。
分别对式(3)中的ω和b求偏导并置零,将结果代入式(3)可得到原问题的对偶问题:

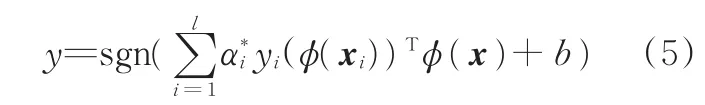
式中,x为测试样本。
定义K(xi,x)=(φ(xi))Tφ(x)为核函数,应用最广泛的核函数即高斯径向基函数:
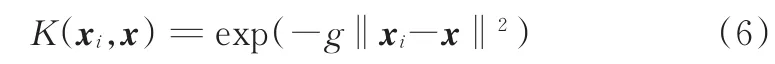
式中,g为核函数宽度。
上述推导过程可以看出,惩罚系数C与核函数宽度g的取值是影响SVM识别性能的主要因素,因此,若要提高识别精度,需确定最优惩罚系数C与核函数宽度g的取值,通常是利用k-cv交叉验证法选择最优的C与g。本文将C与g作为优化对象,以识别精度为适应度函数,利用粒子群优化算法寻找最优的C与g,建立最优的行驶工况识别模型。
1.2 基于粒子群优化的SVM识别算法
粒子群优化(PSO)算法具有搜索机制简单,收敛速度快,运算量小等优点,且能够减少和避免陷入局部最优解的情况。利用基于PSO优化的SVM算法(简称PSO-SVM算法)寻找最优的C和g,可避免k-cv交叉验证法计算量大、精度不高等问题,PSO-SVM算法流程见图1。

图1PSO-SVM算法流程Fig.1 PSO-SVM algorithm flow
PSO-SVM算法的基本步骤如下。
(1)设置种群粒子个数为m。
(2)初始化种群中各粒子的速度和位置,得到第1代种群u(1)=[u(1)1,u(1)2,…,u(1)j,…,u(1)m]。本文的搜索空间为2维,则每个粒子包含2个变量。并将各粒子的历史最优位置pbest设为初始位置,取粒子群全局最优位置gbest中的最优值。
(3)根据得到的种群,更新SVM算法中的惩罚系数C和核函数宽度g。
(4)利用训练样本训练SVM算法模型。
(5)利用测试样本测试SVM算法精度,即适应度函数值。适应度函数值计算表示式如下:

式中,Zrec为识别的工况类型;Zact为实际的工况类型;n为测试样本数量。
(6)更新粒子速度和位置,表达式分别如下:
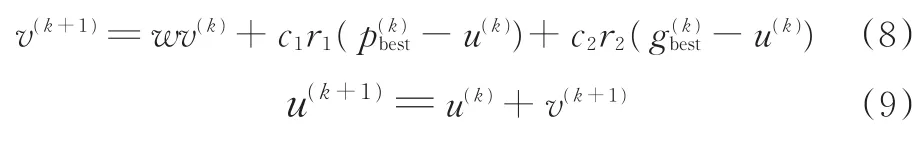
式中,w为惯性权重;r1和r2为分布于区间[0,1]内的随机数;k为当前迭代次数,初始值为1;p(k)best为第k代个体最优粒子位置;g(k)best为第k代全局最优粒子位置;c1、c2为常数;v为粒子速度;u为粒子位置。
进而得到k+1代种群的位置:

(7)计算更新后的每个粒子的适应度,并与之前经历过的最优位置pbest所对应的适应度比较,若当前位置更好,则将其当前位置作为该粒子的pbest。
(8)将每一个粒子的适应度与全体粒子所经历过的最优位置gbest比较,若当前位置更好,则更新gbest的值。
(9)检查终值条件,若精度满足预设条件,则停止迭代;若精度未满足预设条件,则返回步骤(3);若超出最大迭代次数,同样停止迭代。
(10)输出最优解。
2 算法实例分析
2.1 数据采集
在行驶工况识别的研究中,诸多文献都定义了3类典型行驶工况[4,14,16],即市区工况、郊区工况和高速公路工况。但随着城市立体交通网络逐渐形成,高架桥数量逐渐增多。而高架桥道路的行驶工况特点又有别于以上3类行驶工况,因此本文定义4类典型行驶工况,每种工况特点如下:
(1)市区工况。主要集中在城市中心地带,十字路口多,红绿灯多,车辆数目多,交通流量大,道路经常拥堵,车辆频繁启动,车速较低且停车间隙长,工况类型编号为1。
(2)郊区工况。车辆常以中速行驶,停车次数较少且停车时间较短,由于限速,车速不会超过60 km/h,工况类型编号为2。
(3)高架桥工况。车辆常以较高速行驶,双向分割行驶,在无行人或非机动车辆的工况下行驶,无交通信号灯,限速80 km/h,工况类型编号为3。
(4)高速公路工况。与高架桥工况类似,区别在于出入口完全被控制,限制时速比高架桥工况的限速高,通常为120 km/h,工况类型编号为4。
为建立工况数据库,需大量采集符合以上4种工况特征的行驶工况数据。本文以典型中等城市合肥市为例,进行实车道路实验,采集4类典型行驶工况数据。通过整车CAN信号采集设备读取CAN信号中的车辆速度、运行时间、行驶里程等信号,利用车辆综合性能记录仪将信号实时保存在车载电脑中,形成行驶工况数据库。
每类行驶工况的道路实验分别采集6 000组数据,每组数据时长为1 s。对采集的数据进行预处理,对于个别缺失的数据利用插值方法补全,对于产生的奇异值作删除处理,处理后的各典型行驶工况数据见图2。
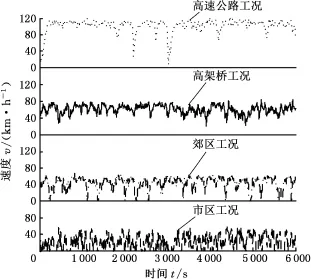
图2 典型行驶工况实验数据Fig.2 Experimental data of typical driving cycle
2.2 样本抽取
为使样本数量充足,保证识别精度,采用随机数法抽取工况样本,具体方法见图3。抽取的样本数据80组,每组数据时长为1 s,即识别周期为80 s。

图3 样本抽取Fig.3 Sample extraction
图3中,ΔT为识别周期;Δω为更新周期;T为该类行驶工况数据总量;t0为样本抽取的起始时刻。每类行驶工况抽取400个样本,共计1 600个样本,抽取的样本起始时刻的表达式如下:

式中,α为产生的随机数,α∈(0,1)。
2.3 样本特征分析
若要保证行驶工况识别的准确性,需确定足够且有效的工况识别输入参数,全面统计和分析工况特征,尤其市区工况行驶速度波动大,经常出现走走停停的状况,因此特征参数既要反映车辆运行快慢特性,又要反映速度波动特性。根据文献[1,17],本文定义14个特征参数描述各工况样本,见表1。
利用MATLAB编程分别求出各典型工况样本的特征参数值,得到样本数量n(行)×特征参数m(列)的矩阵,并按下式进行归一化处理:

式中,Xmax、Xmin分别为样本数据X的最大值和最小值。

表1 行驶工况特征参数Tab.1 Characteristic parameters of driving cycle
定义的14个特征参数之间存在相关性,会对识别模型造成负面干扰,降低识别精度。而主成分分析能够很好地克服参数间的相关性,把多个指标转化为几个综合指标,因此对典型工况样本的特征参数应用主成分分析,得到14个主成分(用Mn表示,n=1,2,…,14)。各主成分的贡献率和累积贡献率见表2。通常选取累计贡献率达到80%以上时所对应的主成分代表所有原始变量进行分析。同时若主成分的特征值小于或等于1,说明该主成分包含的信息量少于或等于直接引入1个原变量的信息量,故选用主成分时,一般要求特征值大于1。由表2可以看出,前3个主成分的特征值均大于1且累积贡献率达到了84.772%,因此选取前3个主成分作为PSO-SVM识别算法的输入参数。各典型工况样本前3个主成分得分见图4。
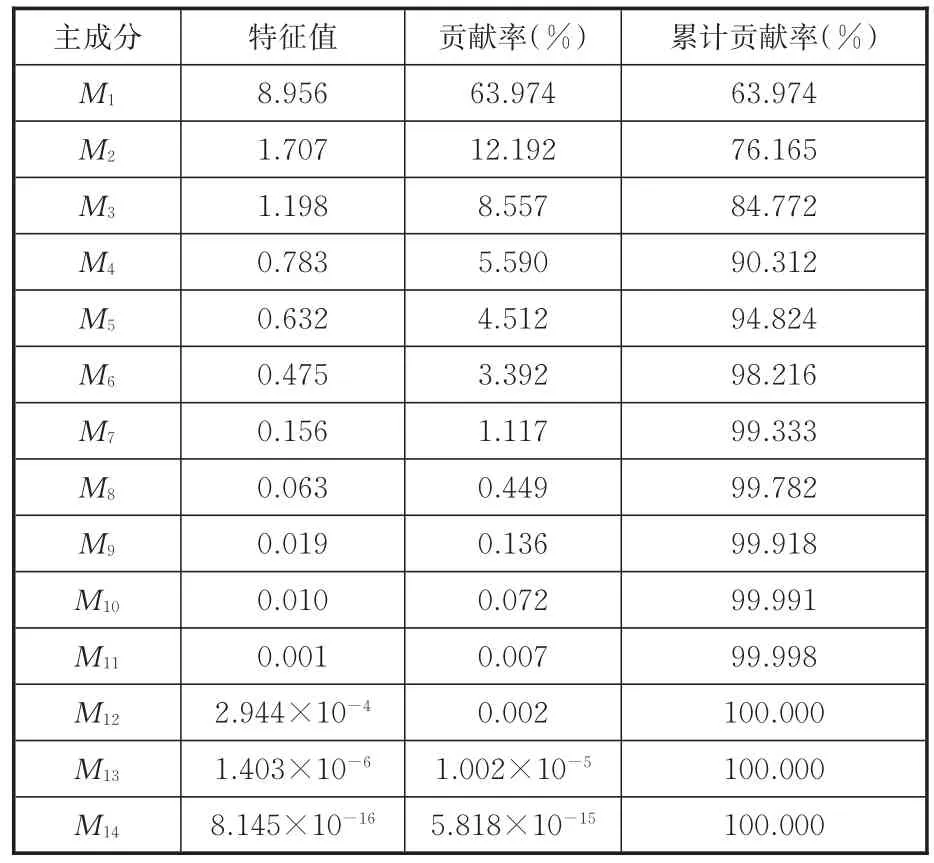
表2 各主成分贡献率和累积贡献率Tab.2 The contribution rate and cumulative contribution rate of principal component
2.4 基于PSO-SVM算法的行驶工况识别模型

图4 各典型工况样本主成分得分Fig.4 The principal component scores of typical driving cycle sample
上述3个主成分作为PSO-SVM算法的输入参数。从1 600个主成分得分样本中随机抽取80%作为训练样本,建立识别模型;剩下20%作为测试样本,验证识别模型的精度。粒子群算法种群规模设置为20,最大迭代次数为100。将基于PSO-SVM算法和基于k-cv交叉验证法建立的SVM识别算法进行比较,以评价PSO优化后的识别效果。k-cv交叉验证法中将C、g分别取以2为底的指数离散值,即 C∈{2-10,2-9,…,29,210},g∈{2-10,2-9,…,29,210},进行网格寻优,分别取识别精度最高时所对应的C、g值作为最优值。PSOSVM算法的迭代过程和k-cv交叉验证法寻优过程分别见图5和图6。
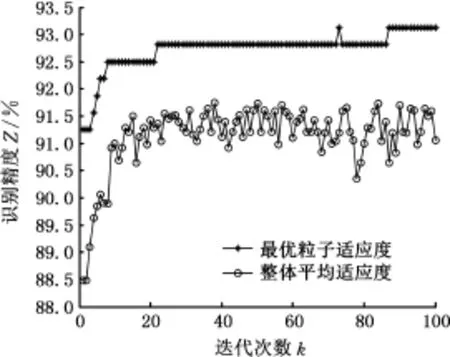
图5 PSO-SVM算法的迭代过程Fig.5 The iteration process of PSO-SVM algorithm

图6 k-cv交叉验证法寻优过程Fig.6 The optimization process of cross validation based on k-cv
由图5可以看出,经过100次迭代,PSO-SVM算法寻得最优粒子时的识别精度为93.125%,对应的最优粒子C=4.433,g=7.126。而k-cv交叉验证法识别精度最高为88.994%,对应的最优粒子C=0.25,g=16。由此可见,基于PSO-SVM算法的行驶工况识别精度提高了4.131%。两种算法的320个测试样本的识别结果见图7,可以看出,两种情形下,高速公路工况的识别错误率最低,郊区工况的识别错误率最高。而基于PSOSVM算法建立的识别模型在市区、郊区和高架桥工况的识别精度均高于k-cv交叉验证法的识别精度,而在高速公路工况下,2种算法的识别精度接近。

图7 测试样本识别结果Fig.7 Test sample recognition results
3 识别周期及更新周期对行驶工况识别精度的影响分析
在识别模型的建立过程和在线应用中,识别周期ΔT和更新周期Δω存在不确定性。ΔT的大小决定样本数据时长,进而决定样本所含信息量,ΔT过小,获得的工况信息量较少,可信度降低;ΔT过大,无用的信息增多,不利于反映参数特征。而Δω的大小决定工况信息更新的快慢,Δω过小,则计算量增加,对处理器要求提高,且可能导致识别的工况频繁切换;Δω过大,则工况识别的灵敏度降低,不利于实时最优控制。由此可知,选取合适的识别周期和更新周期是准确识别工况的保证。本文分别选取ΔT=30 s、80 s、130 s、180 s抽取样本,应用PSO-SVM识别算法和基于k-cv交叉验证法的SVM识别算法建立识别模型,并以一段随机组合行驶工况为例,分别考虑Δω=5 s、10 s、20 s时,对随机工况进行实时在线识别,比较识别结果,并确定最优ΔT和Δω,随机行驶工况见图8。篇幅限制,只列举了ΔT=80 s、Δω=10 s时的情况,2种算法在线识别结果见图9。根据式(7)对识别结果进行统计,其中PSO-SVM算法的识别精度达到了91.089%,而基于k-cv的SVM算法的识别精度为83.168%,PSO-SVM算法的精度提高了7.921%。
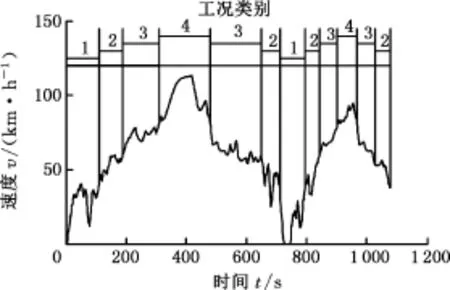
图8 随机行驶工况Fig.8 Random driving cycle

图9 在Δ T=80 s、Δ ω=10 s时的在线识别结果Fig.9 Online recognition results when ΔT=80 s,Δ ω=10 s
通过一系列重复交叉试验来获取最优ΔT和Δω,2种算法下所有组合在线识别结果见图10和图11,可以看出,PSO-SVM识别算法的精度普遍高于基于k-cv的SVM识别算法的精度。ΔT增大时,PSO-SVM算法的识别精度均有所提高,但当ΔT进一步增大时,PSO-SVM算法的识别精度有下降的趋势,这也符合前文提及的识别周期过小或过大均不利于实时在线识别的分析。当ΔT=30 s和180 s时,2种算法的识别精度均随Δω的增大而降低;当ΔT=80 s和130 s时,PSO-SVM算法的Δω取中间值10 s时,识别精度最高。综合以上分析,在ΔT=80 s、Δω=10 s时,PSO-SVM算法的识别精度达到90%以上,可依据此确定ΔT和Δω数值。

图10 PSO-SVM算法在线识别精度Fig.10 PSO-SVM algorithm online recognition results
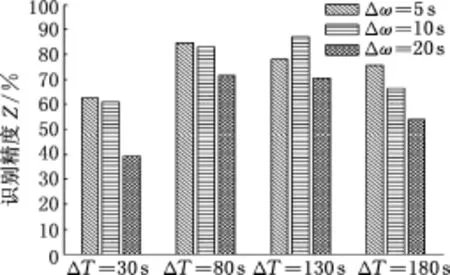
图11 基于k-cv的SVM算法在线识别精度Fig.11 SVM algorithm online recognition results based on k-cv
4 行驶工况识别在混合动力汽车能量管理策略的应用分析
4.1 基于行驶工况识别的能量管理策略
行驶工况对混合动力汽车的燃油经济性有较大的影响[1],因此为进一步提高整车燃油经济性,能量管理策略应根据当前行驶工况的特点,实时调整策略控制参数值,以实现不同动力源功率分配的实时最优。等效燃油消耗最小策略(equivalent fuel consumption minimization strategy,ECMS)具有结构简单、运算量小、无需先验知识的优点,且通过引入惩罚函数,使得该策略具有良好的电量保持特性,可较好地适用于插电式混合动力汽车的电量保持阶段的能量管理,因此被广泛研究[18-19]。
ECMS控制思想是:根据整车的实际驾驶员需求功率,在发动机和电机的功率范围内合理分配发动机和电机的实际输出功率,使得发动机瞬时燃油消耗率和电机消耗电量的等效燃油消耗率的总和最小,即

综上所述,若要将行驶工况识别应用到ECMS中,需提前获得各典型工况下ECMS最优充电等效因子和放电等效因子。针对以上问题,以降低燃油消耗量为优化目标,建立基于P2构型的某插电式混合动力汽车Simulink模型,整车构型见图12,整车及能量管理策略顶层Simulink模块见图13,动力及传动系统参数见表3。

图12 某插电式混合动力汽车整车构型Fig.12 Configuration of a plug-in hybrid electric vehicle

图13 整车及能量管理策略顶层模块Fig.13 Top-level module of vehicle and energy management strategy
利用Simulink模型描述充放电等效因子与目标参数之间的非线性关系,并采用智能优化算法获得各典型工况及综合工况下ECMS最优充电等效因子和放电等效因子,见表4。

表3 动力及传动系统参数Tab.3 Power and transmission system parameters

表4 各典型工况最佳充放电等效因子Tab.4 The optimal charge and discharge equivalent factor in the typical driving cycle
4.2 基于行驶工况识别的ECMS仿真分析
为了对比分析,考虑3种情形,即未采用行驶工况识别的ECMS、基于k-cv的SVM行驶工况识别的ECMS及基于PSO-SVM算法行驶工况识别的ECMS(简称为模式一、模式二和模式三)。将随机行驶工况在ΔT=80 s、Δω=10 s时的各识别结果序列导入Simulink整车模型中的能量管理策略模块内,利用Switch模块切换充放电等效因子数值。仿真整车在电量保持阶段的性能,初始SOC值设定为0.63,电池SOC值上下限分别为0.7和0.6。仿真过程车速跟随情况见图14,可以看出,3种模式下的ECMS均满足车辆需求功率,实际车速与目标车速基本吻合,车速跟随误差较小。

图14 车速跟随情况Fig.14 Velocity following condition

图15 累积燃油消耗量Fig.15 Cumulative fuel consumption

图16 SOC变化曲线Fig.16 The curves of SOC
模式一~模式三时的累积燃油消耗量和SOC变化曲线分别见图15和图16。分析图15可知,模式一时策略累积燃油消耗量为732 g,百公里油耗为5.343 L;模式二时策略累积燃油消耗量为690 g,百公里油耗为5.042 L,相对于模式一,燃油经济性提高了5.634%;模式三时策略累积燃油消耗量为660 g,百公里油耗为4.817 L,相对于模式一,燃油经济性提高了9.836%,而相对于模式二亦提高了4.348%。电池荷电状态(SOC)用参数Ssoc表示,其数值表示剩余电量占比,1表示电池充满电,0表示电池放完电。由图16可知,3种模式下的SOC保持性能均较好,与目标SOC值偏差均在5%以内,但模式一时的电池SOC波动较大,充放电次数较多。模式二与模式三时的SOC变化相对平稳,且电池充放电次数减少,有利于提高系统效率和延长电池寿命。
5 结论
(1)分析了合肥市交通特征与道路特征,分别在代表市区工况、郊区工况、高架桥工况和高速公路工况的道路进行实车实验,采集大量行驶工况数据。定义了描述行驶工况特性的特征参数,利用多元统计理论对数据进行了处理,提取出可用于行驶工况识别的参数。
(2)建立基于粒子群优化的SVM识别算法,并通过实例分析可知,PSO-SVM算法识别精度比基于k-cv交叉验证法的SVM算法的识别精度高。讨论了行驶工况识别过程中,识别周期和更新周期对识别精度的影响,结果表明在识别周期为80 s、更新周期为10 s时,识别精度最高,但仍需进一步提高。
(3)将行驶工况识别技术应用到插电式混合动力汽车的能量管理策略中。仿真结果表明,相对于未采用行驶工况识别及基于k-cv交叉验证法的SVM识别,PSO-SVM算法可有效提高整车燃油经济性,且电池SOC的波动相对平稳,可提高系统效率。
