抓住精彩“意外” 开展探究创新——关于抛物线的焦点弦性质案例

范雪飞

(浙江省永嘉第二高级中学 325100)

新课程强调培养学生的探究创新精神，我们老师觉得手上没有什么素材，再说这种精神的东西往往很空泛，不知从哪里入手.其实我们的学生在这方面给了我们很多素材，上课的时候很多学生有很好的想法，关键是我们教师该如何抓住这一瞬间的精彩，能够让学生的探究创新进行下去.看老师“给力不给力”.通过指导学生积极探究的方式，引导他们亲历知识的产生和发展过程，形成自身的认知结构，体验发现和创造的历程.

本案例以抛物线焦点弦性质为题材，说一说自己的看法.

案例描述如图1，AB是抛物线y2=2px(p>0)的一条经过焦点F的弦，AB与两坐标轴不垂直，已知M(-1,0),∠AMF=∠BMF，则p的值为( ).

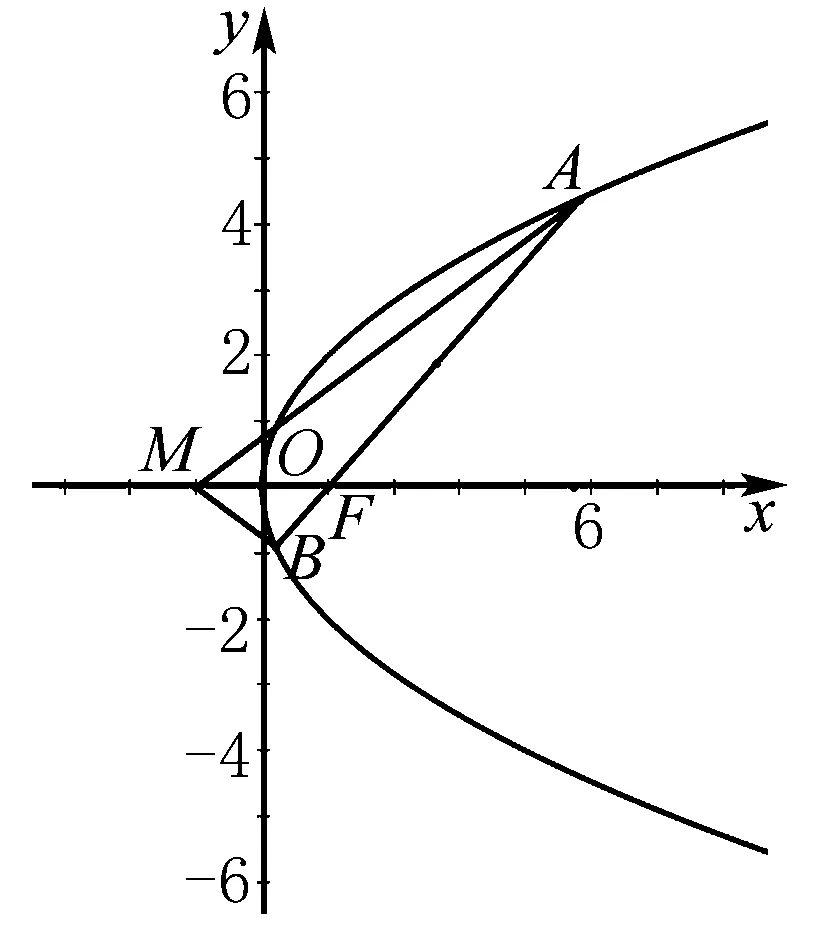
图1

问题背景分析作为授课的切入点，考虑本题的难度，若以解答题的形式要求从正面解决，是操之过急的，而且会给学生带来一定的心理受挫感，削弱学习的积极性.而对于选择题，除了从正面解决之外，还有猜想、代入检验等方法，易于得到答案.

果然，出示题目几分中后，有两位同桌就开始相互讨论起来，还用稿纸相互交流，看起来是有想法了.我走到边上，未等我开口，生①就主动和我交流起来.

生①：老师，是选C吧？

师：你是选哪个呢(问生②)？

生②：我也觉得是C.

同时查阅生②正在写的稿纸，是未完成的检验过程，基本思路整理如下：

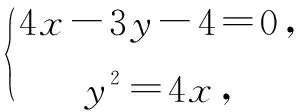
师：看来你俩是猜想的，答案是选C.

给了一个赞许的答复后，回身一边察看其余学生的情况，一边想着开题讲解可以由生②分析引入了，“算计”着他应该差不多检验完毕，便窃喜着跺回讲台.

师：看来，大家都有了心仪的选项.生②同学，请你来谈谈，你选哪个？

生②：C.

师：那你是怎么选出来的？

生②：猜的.

师：答案是C.不过猜想也得有一定道理，不能随意的.你是怎么猜出来的？

生②：因为从这个图形看，点M和F是对称的.

师：哦，所以你就认为焦点F坐标为(1，0)，从而p=2了.那有检验过吗？

生②：差不多，还没做完.

在这样的对话中，组内其他同学已经知道生②是怎样得到答案，有些也笑了，估计是觉得生②同学的解题方法太草率.因此，我将他的稿纸内容投影到屏幕上，师生一起来研究他的检验：

(续上面的检验步骤)

肯定生②的猜想后，再回过头来分析整个过程，在引导下共同总结得到以下两个要点：

(1)∵∠AMF=∠BMF，∴kMA+kMB=0.

(2)鉴于在抛物线上取点A的任意性，结论与直线AB的斜率无关.

师：但在检验的基础上，以上两点只是猜想，对本题来讲我们仍未给予正确的解答过程.从大体上看来，既然题目与直线AB的斜率没有关联，就可以大胆地设斜率为k.而由∠AMF=∠BMF得到的等式kMA+kMB=0也可以仅被p表示，从而得到关于p的方程，最终解出p的值是多少.

师生共同分析，教师主导，给出解答过程.

意外通过上面的计算，我们已经确认此结论是与直线的斜率无关的.这时有同学就说了：“这是一个与直线斜率没有关系，只有和所选取的点有关系，那么对于一个抛物线来讲，特殊点M与任意焦点弦的端点形成的角度是否就一定相等呢？”

我一下子就愣住了，这个问题是我没有思考的，但是我感觉这应该是一个定值于是我就引导他们探索：请同学们就以y2=4x为例再做一次大胆的检验证明.已知：抛物线y2=4x，F是抛物线的焦点，AB是抛物线的焦点弦，M是抛物线准线与x轴的交点，则∠AMF=∠BMF.

给予学生思考时间，生③的证明过程：

生④：AB没有斜率的情况漏了.

师：对，那你认为斜率不存在的时候结论还成立吗？

生④：成立的.这时图象是对称的.

师：非常好！这里并没有讲直线AB不垂直于x轴，所以同学们要注意，平时解题要谨慎，要做到不重不漏.因此，我们可以发现∠AMF=∠BMF这个结论成立确实和直线AB的斜率是没有关系的，只要AB是抛物线的焦点弦，M是抛物线准线与x轴的交点，则一定有∠AMF=∠BMF.

猜想1 已知抛物线y2=2px(p>0)，F是抛物线的焦点，AB是抛物线的焦点弦，M是抛物线准线与x轴的交点，则∠AMF=∠BMF.

教师归纳师生共同回顾上述猜想探究的过程，变换条件到结论成立的成功过渡，有一个不小的收获.让学生经历了从变换条件到结论成立的探究过程，从直线是抛物线焦点弦这一特殊性质出发，“再创造”出关于此类抛物线焦点弦性质的全过程.这一过程让学生真实地体验到了“探究——创新”学习的快乐，值得认真总结，值得高兴一番.

猜想2 已知抛物线y2=2px(p>0)，F是抛物线的焦点，M是抛物线准线与x轴的交点，AB是一条与抛物线上下半支都有交点的直线，交点是A，B，若∠AMF=∠BMF，则AB过抛物线的焦点.

已知抛物线y2=4x，F是抛物线的焦点，M是抛物线准线与x轴的交点，AB是一条与x轴不垂直的直线，且与抛物线上下半支都有交点，交点是A，B.若∠AMF=∠BMF，求证AB过抛物线的焦点.

同学们很快仿照上面的过程给出了结论：

证明：设直线AB方程为y=k(x-a)，抛物线y2=4x，点A(x1,y1),B(x2，y2) .

两式联立，化得k2x2-(2ak2+4)x+a2k2=0,

由∠AMF=∠BMF,知kMA+kMB=0,

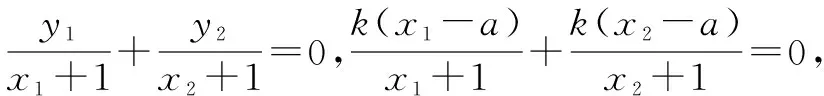
代入2x1x2+(1-a)(x1+x2)-2a=0.

去分母，化简后可得a=1.

所以直线AB过抛物线的焦点F(1，0).

教师归纳由前面的猜想得到结论我们发现它和三个条件有关，即AB是过抛物线焦点的直线；点M是抛物线准线与x轴的交点；∠AMF=∠BMF.是不是只要这三个条件里满足其中两个，另一个就成立呢？于是有了下面的猜想：

猜想3 已知抛物线y2=2px(p≥0)，F是抛物线的焦点，AB是抛物线的焦点弦，点M是x轴负半轴上的点，若∠AMF=∠BMF，则点M是抛物线准线与x轴的交点.

已知：抛物线y2=4x，F是抛物线的焦点，AB是抛物线的焦点弦，点M是x轴负方向上的点，若∠AMF=∠BMF，求证：M是抛物线准线与x轴的交点.

证明：设直线AB方程为y=k(x-1)，点A(x1,y1),B(x2,y2)，点M的坐标为(a,0).

得：k2x2-(2k2+4)x+k2=0,

∵∠AMF=∠BMF，所以kAM=-kBM,

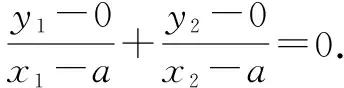
又∵x1>a,x2>a⟹y1(x2-a)+y2(x1-a)=0,

即2kx1x2-k(x1+x2)-ak(x1+x2)+2ak=0.

当k=0时，结论显然成立.

当k≠0时，上式可化为

k[2x1x2-(1+a)(x1+x2)+2a]=0,

即2k2-(1+a)(2k2+4)+2ak2=0,

得4a+4=0，a=-1.

即M点是抛物线准线与x轴的交点.

案例分析在研究过程中发现直线AB的斜率k与运算无关，与三个条件有关，即AB是过抛物线焦点的直线；点M是抛物线准线与x轴的交点；∠AMF=∠BMF.只要满足了其中两个另外一个可以推导出来.通过这三个条件的互相转化形成条件和结论.在“探究——创新”过程中培养学生的数学思维和创新意识.在圆锥曲线教学中，尤其是鼓励学生由特殊到一般的直觉猜想.对圆锥曲线的相关问题，应鼓励学生根据方程形式、图形特征进行直觉猜想；通过对特殊情景的研究引发从特殊到一般的归纳思想.并在此基础上，从不同的角度进行逻辑探索，以此达到从各个侧面、不同层次上提高学生数学素养的目的.

如何能做到“给力”探索创新，这就对我们教师提出了新的要求需要教师在更高的理论水平下抓住学生的“意外”能及时的加以拓展延伸.真正做到“给力”的教师关键的是课后的工作，通过本案例笔者谈谈自己的几点看法：

案例反思1真正的数学课堂应该是师生之间的一种对话交流

巴西教育家保罗.弗莱雷说：没有对话，就没有交流，也就没有真正的教育.新课程要求教学是平等的、民主的，要构建起共同探讨的学习环境；新课程还指出教师应是学生亲密的伙伴，对学生在学习过程中的表现应该给予充分的理解与尊重.因此在课堂上，教师要注意倾听，理顺学生的思维过程，解决学生学习中的的疑难问题，注意引导发现问题，引导学生合作探究.

案例反思2不要快节奏的上课，慢慢又何妨

而新课程背景下要求教师要培养学生自己找“路”的能力，让学生做“司机”，而不是“乘客”.教师做一个“指路人”，在学生迷路时，给予指点、点拨.学和行走的过程中，路边的风景，正是学生找到回路的标志.让我们记住关于教育的一句世界名言——告诉我，我会忘记；分析给我听，我可能会记住；如果让我参与，我会真正的理解.

案例反思3积极鼓励学生自主探究发现，给学生的“意外”以肯定

在探究解题方案和解法时，每一位学生都在积极思考、参与探究，课堂的学习氛围是民主的、开放的、和谐的，对问题的分析大家都是争先恐后的.教师要用自己情感激发学生的情感，用自己的智慧启迪学生的智慧，用自己的思维引导学生的思维.课堂教学是动态的双向交流，其中成功的愉悦、艰辛的探索给每位学生带来一种激情，鼓励着学生去探究知识的发生、发展过程，体验解题过程中的各种感悟.

案例反思4教师要提高研究题目的意识、增强研究题目的能力，对“意外”有较强的控制和突破能力.

课堂中要有高效的抓“意外”的能力，做“给力”的教师就要在平时要培养自己研究试题的能力.教师在长期的教学时间中，形成了自己独特的经验性思维.教师不要忘记时刻努力提高自己的专业能力，不要让经验淹没了自己研究试题的热情，不要让资料淡化了自己研究试题的意识.

培养学生的创新意识不是一朝一夕就可以培养出来的，这是一个长期而复杂的系统工程.教师应当在平时的教学中，把习题的开发作为“探究——创新” 教学的切入点，为学生学会创新提供适宜的平台，在“探究——创新”做“给力”的教师教学过程中，深入探究，体验再创，力求出新，创新意识才可能在学生的头脑中扎根，才有可能培养出具有创新精神和创新能力的一代新人.