简谐运动合成的讨论

金 锋 丁亚明 朱亚敏 黎振远

(天津天狮学院 300011)

振动是一种周期性的运动，简谐运动是最简单、最基本的振动.复杂的振动可以分解为简谐运动的叠加，研究两个简谐运动的叠加有重要意义.两个简谐运动的合成主要有同方向同频率、同方向不同频率、相互垂直同频率和相互垂直不同频率等几种情况.两个同方向同频率简谐运动的合成，仍然是一个简谐运动；两个同方向不同频率简谐运动的合成，在频率差与原有频率相比非常小时形成拍；两个相互垂直同频率简谐运动的合成，轨迹方程是一个椭圆，也可以退化为圆或者直线；两个相互垂直不同频率简谐运动的合成，形成李萨如图形.本文主要研究两个相互垂直同频率简谐运动的合成，用三角函数的化简和反三角函数的方法的推导合成后运动方程.

一、同方向同频率两个简谐运动的合成

在同方向同频率两个简谐运动的合成时，合运动是一个新的简谐运动.合运动的角频率与原有简谐运动相同，合运动的振幅和初相由两个原有简谐运动的振幅和初相位决定.

两个同方向同频率的简谐运动，它们的简谐运动方程分别为：

合运动可以用旋转矢量的方法求出，如图1.

它的简谐运动方程为：

x=Acos(ωt+φ)

振幅：

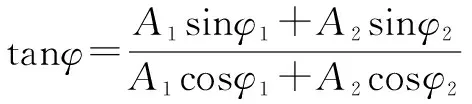
二、同方向不同频率两个简谐运动的合成

有两个同方向不同频率的简谐运动，它们的简谐运动方程分别为：

根据三角函数的和差化积，合运动的轨迹方程为：

x=x1+x2

三、相互垂直同频率两个简谐运动的合成

有两个相互垂直的同频率简谐运动，它们的简谐运动方程分别为：

消去时间t，可得合运动的轨迹方程为：

1.利用三角函数的化简推导椭圆方程

根据三角形的和差关系，整理(1)和(2)

(4)乘以cosφ2，(5)乘以cosφ1后得：

(8)两边平方得：

(4)乘以sinφ2，(5)乘以sinφ1后得：

(10)和(11)做差得：

(12)两边平方得：

=cos2ωt·sin2(φ2-φ1) (13)

(9)和(13)两式两边分别求和，整理后得：

上式为相互垂直同频率两个简谐运动合成的轨迹方程，即：椭圆方程.

2.利用反三角函数推导椭圆方程

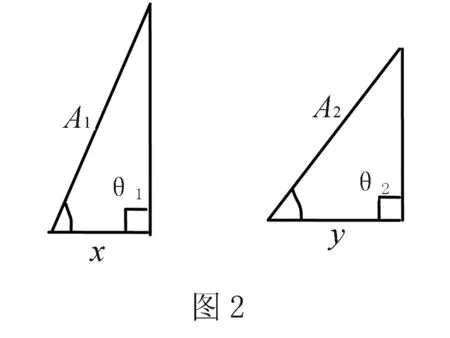
为了计算方便，建立两个直角三角形，如图2 ，有

根据(17)和(18)的关系，(15)与(16)两边做差，整理后得：

θ2-θ1=φ2-φ1(19)

对(19)两边取正弦，得：

sin(θ2-θ1)=sin(φ2-φ1) (20)

对(20)两边平方，得：

sin2(θ2-θ1)=sin2(φ2-φ1) (21)

根据三角函数的性质，整理(21)后得：

sin2θ2·cos2θ1-2sinθ2·cosθ1·cosθ2·sinθ1+cos2θ2·sin2θ1=sin2(φ2-φ1) (22)

把(17)和(18)代入(22)左面，整理后得：

上式与(22)式联立，即

四、相互垂直不同频率两个简谐运动的合成

两个相互垂直不同频率的简谐运动合成，两个原有频率为整数比时，形成李萨如图性；当两个原有频率之比为无理数时，将发生同步锁模现象.

两个简谐运动的合成是非常复杂的过程，合成过程主要包括振动方向的平行与垂直；频率相等与不相等等几种情况，本文从振动方向和频率的异同出发，得出合运动的运动方程，主要介绍了相互垂直同频率两个简谐运动合成轨迹的推导过程，分别用三角函数的化简和反三角函数等方法均得出合运动的轨迹方程，即椭圆方程.