高中数学函数问题的探究

尹学明

(浙江省台州市第一中学 318000)

一、函数与方程

函数和方程具有密切的联系，方程的解其实是函数图象与x轴的交点.函数y=f(x)可以当做方程f(x)-y=0进行分析和探究，在函数的变化中，有时候需要通过方程来求出满足条件的一些关键量，这就是方程思想.函数与方程是贯穿于学生整个高中阶段的，引导学生进行数学量与量之间关系的分析和探究，并将这些变化反映到解析式、图象以及列表中，从而让学生更容易地进行问题的理解和解决.高中方程可以用f(x)=0或f(x)=g(x)的形式表示，f(x)=0的根就是函数y=f(x)图象与x轴的交点，f(x)=g(x)的根就是函数y=f(x)与y=g(x)图象交点的横坐标.

例1 (2016年浙江高考12题)设函数f(x)=x3+3x2+1.已知a≠0，且f(x)-f(a)=(x-b)(x-a)2,x∈R，则实数a=____，b=____．

解析本题主要体现了函数和方程的思想，在掌握函数解析式的情况下，将x与a分别代入函数中，得出f(x)-f(a)=x3+3x2-a3-3a2，然后再为(x-b)(x-a)2化简即可构造出有关a、b的方程组，从而求解.

二、函数与不等式

函数思想在不等式的分析和解答中也具有重要的意义，可以通过不等式的信息进行函数的构造，然后用函数的性质和图象进行分析，往往能起到事半功倍的效果.高中的不等式基本上可以用f(x)>0、f(x)<0或是f(x)>g(x)进行表示，当然也可以在图象上通过上下位置的关系进行阐述.

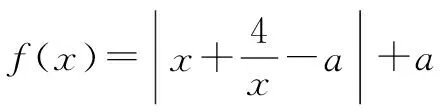
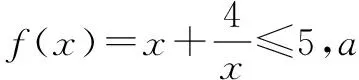
当4+a,|5-a|>+a},由此可知：

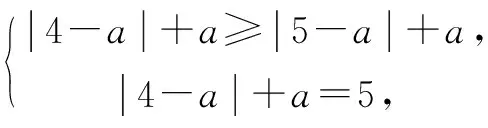
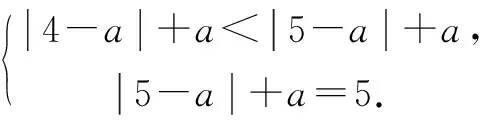
三、函数与导数

导函数是高考的重要内容，尤其是一些简答试题中，常常有导函数的问题，这就要求学生要运用函数思想进行导函数单调性、极值的问题分析和解决，同时能够将函数的各种形式进行转化，从而对有关导函数的问题能够从容应对.

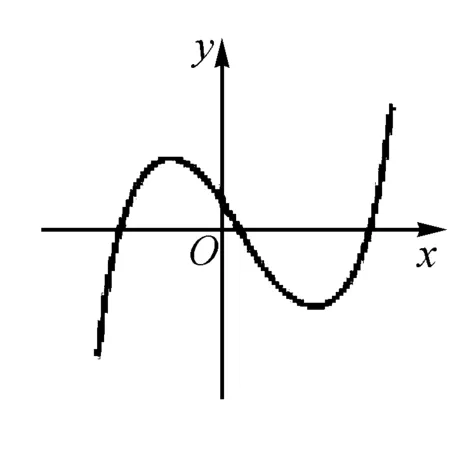
例3 (2017浙江高考7题)函数y=f(x)的导函数y=f′(x)的图象如图所示，则函数y=f(x)的图象可能是( ).

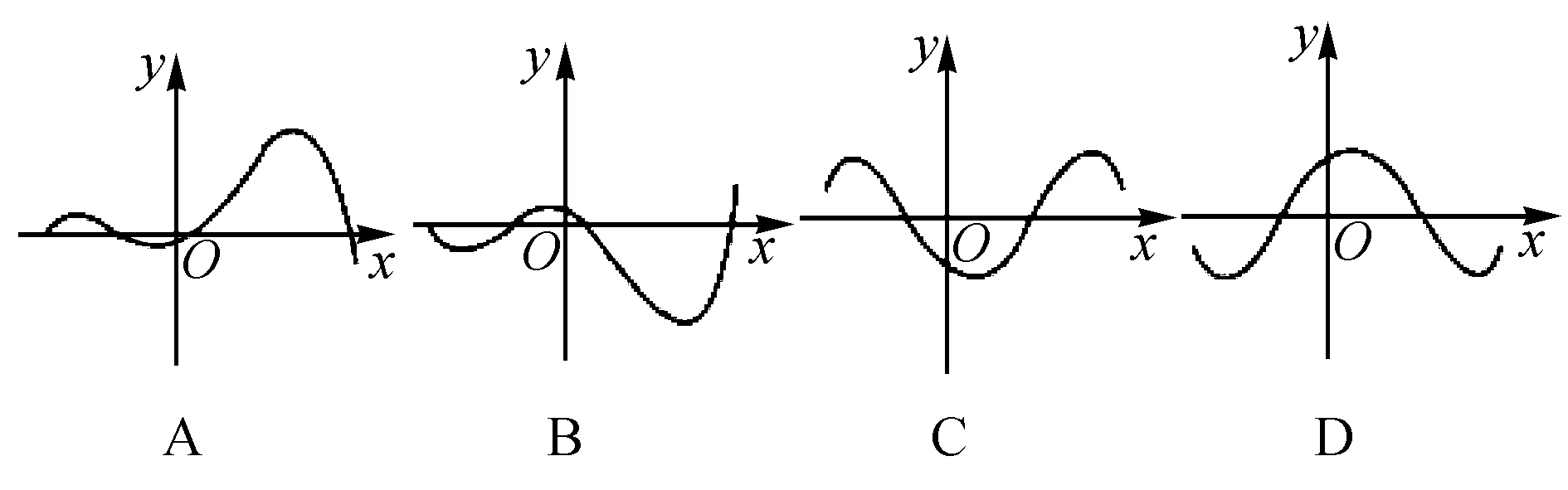
解析本题主要要求学生能够从导函数的图象进行函数图象的判定，由导函数的性质可知，f′(x)<0，函数单调递减，f′(x)>0函数单调递增，由导函数的图象可知，原函数先递减再递增，然后在递减再递增，由此可以得出答案.

(1)求f(x)的导函数；

解析本题第一问直接通过函数求导得出结果即可，第二问需要运用第一问中的导函数，进行原函数极值和单调性的计算，同时满足f(x)≥0的条件，则可以确定f(x)的取值范围.

总之，从近几年浙江高考的趋势来看，函数思想在高考中占有绝对的比例，就拿2017年高考来说，浙江试题中一共有5题，知识点涉及二次函数、方程、不等式、导函数、三角函数、函数模型等，这就要求教师在教学的时候，要结合教学内容，将函数思想贯穿在数学教学的始终，培养学生运用函数进行具体问题的分析和解决，从而提升学生数学能力，促进学生数学素养的全面发展.