基于圆的定义 发挥直观想象*

福建省惠安第三中学(362100) 江志杰 庄银泉

《关于普通高中数学课程标准修订》的专题报告,提出中国学生在数学学习中应培养好数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大核心素养.其中直观想象是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程.主要包括:借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立数与形的联系,构建数学问题的直观模型,探索解决问题的思路.另外,直观想象也是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.因此,在直观想象核心素养的形成过程中,学生能够进一步发展几何直观和空间想象能力,增强运用图形和空间想象思考问题的意识,提升数形结合的能力,感悟事物的本质,培养创新思维.如何落实以知识为载体、以素养为目标的学科教学呢?下面笔者根据中学阶段圆的若干定义,谈谈如何构造圆的轨迹直观简捷地化解相关数学问题,并且在分析和解决问题中体验直观想象核心素养的形成及其意义!

一、从原始定义构造圆

中学阶段圆的最基本定义:平面内到定点的距离等于定长的点的轨迹是圆,其中定点和定长分别为该圆的圆心和半径.据此,我们经常借助“距离”模型来形象看待有关含向量(或复数)模的方程,进而构成圆的轨迹雏形.比如复数z满足|z|=1,则复数z对应的点落在单位圆上;又如向量满足则向量的长度为2,当其中点B的位置固定时,点A落在以点B为圆心、半径为2的圆上…….我们平时就要有这样数形结合、动静相辅的眼光以及直观想象的素养,来观察、理解、分析各类不同方式表达的数学问题,增强直观转化、形象化解的能力!

另外还有EW向和近SN向断裂组：为区内早期断裂，规模小，数量少，个别地段密集出现，被后期断裂组所切穿。

例1 已知a,b是单位向量,a·b=0,若向量c满足|c−a−b|=1,则|c|的取值范围是____.

解析本题|c−a−b|=1即|c−(a+b)|=1,可理解为动向量c的终点P与定向量a+b的终点M的距离为1(两向量的起点均为原点O),由单位正方形模型易得不妨将向量a+b的终点M固定在点则点P在以点M为圆心、半径为1的圆上运动,易得从而使得本题在直观形象的模型中轻易地化解,具备直观想象这一核心素养其实就是我们构建合理数学模型的思维基础!

例2 直线l:y=kx+4−3k(k∈R)与函数的图像交于A,B两点,点P(x,y)是坐标平面上的点,满足则x2+y2的取值范围是____.

解析由于函数表示对称中心为O′(3,4)的双曲线,直线l:y=kx+4−3k(k∈R)即y−4=k(x−3)恰好恒过点O′(3,4),故A,B两点关于点O′对称,从而可化为说明点P在以点O′为圆心、半径为1的圆上运动,所以本题关键点O′(3,4)是一大核心枢纽,使得直线方程、双曲线解析式、向量模的关系式三者之间一脉相承,最终由圆的定义汇聚于圆这一常见模型!可见发挥直观想象这一核心素养,要求我们善于通过数学运算、变形变式、直觉猜想、数学抽象等过程,从数学问题中挖掘、捕捉有用的数学信息,才能将抽象费解的数学问题置换于形象直观的几何背景下解决!

例3 (2018年宁德市高三质检)设函数f(x)=|x2−2x−1|,若a＞b≥1,f(a)=f(b),则对任意的实数c,(a−c)2+(b+c)2的最小值为___.

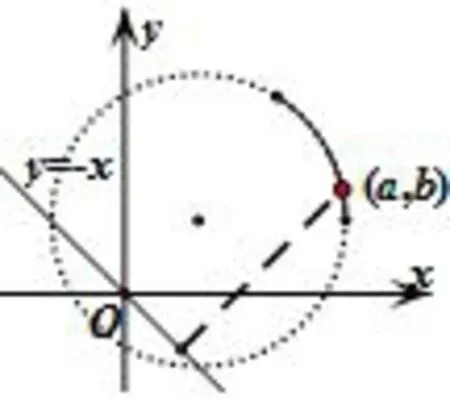
图1

解析本题目标“(a−c)2+(b+c)2”给我们最直观的印象–表示点(a,b)与点(c,−c)之间距离的平方,注意到实数c的任意性,进而理解为动点(a,b)到定直线y=−x的距离平方,这是顺利解决本题的首要具备的基本素养所在!结合函数f(x)的图像,由a＞b≥ 1,f(a)=f(b)化简得a2−2a−1=−(b2−2b−1),整理配方得到:(a−1)2+(b−1)2=4(其中其表示点(a,b)位于圆心为(1,1)、半径为2的一段圆弧上—这又是成功解决本题的一大关键模型!如图易得点(3,1)到直线y=−x的距离最小,当然在本题解法中,圆的模型毕竟较为隐蔽深邃,可见直观想象的素养形成有利于我们借助几何图形的形象关系去描述相对复杂、抽象的问题,也就是将研究问题图形化,促进对数量关系的直观感知和宏观把握!

二、从垂直关系构造圆

值得一提的是上述基本定义并非构成圆的唯一方式,还有如下的常见表达:

平面内对两个定点的张角为直角的点的轨迹是以这两个定点连线为直径端点的圆(不含这两个定点).注意该定义又有以下的等价变式:

平面内,若动点P与两个定点A,B连线的斜率之积为−1,则动点P的轨迹是以AB为直径的圆(不含定点A,B和斜率为零时的点);

平面内,若动点P与两个定点A,B满足则动点P的轨迹是以AB为直径的圆;

取100 μL链霉亲和素修饰的微球(直径为15.4 μm)于0.5 mL的灭菌离心管中,用100 μL的亲和洗脱液(pH 7.5,20 mmol/L Tris-HCl,1 M NaCl,1 mmol/L EDTA,0.0005% Triton X-100)洗涤两次,3 500 r/min离心分离后去上层清液。向微球中加入47 μL的亲和洗脱液以及3 μL的Hg2+捕获探针(10μM),混合均匀并37 ℃摇床孵育1 h。通过离心洗涤除去未结合的探针,加入100 μL亲和洗脱液于4 ℃下保存备用。

例8 已知等腰三角形腰上的中线长为2,则该三角形的面积最大值是___.

上述从垂直关系构造圆的轨迹,还可以进行一般化的推广和补充.我们知道圆具有这样的性质:在圆内,同弧(或同弦)所对的圆周角相等.反之,平面内对两个定点的张角为定值的点落在以两个定点连线为弦的一侧圆弧上,于是即有:

解析本题入手首要在于从两个含参的直线方程中发现l1⊥l2,意味着点M在以定点A(0,0),B(1,3)为直径端点的圆上运动,而|MA|·|MB|的几何意义表示Rt△MAB面积的2倍,因此借助几何直观有:|MA|·|MB|=|AB|·dM−AB≤ 2r2=5.这就说明垂直关系往往蕴含着圆的模型,其就是我们构造圆解题的重要依据!

例5 已知两点A(−m,0)和B(m+2,0)(m＞0),若在直线l:上存在点P,使得PA⊥PB,则实数m的取值范围是()

变式在△ABC中,内角A,B,C的对边分别是a,b,c,且则△ABC面积的最大值是____.(答案:2)

解析若能注意到点P落在以AB为直径的圆(x−1)2+y2=(m+1)2上,则问题转为直线l:与该圆存在公共点,由得m≥3.故选C.可见构造圆这一经典模型有助于化解问题的抽象性、提升数形结合的直观性.类似地,本题还有如下变式:

变式已知圆C:(x−3)2+(y−4)2=1和两点A(−m,0),B(m,0)(m＞0),若圆上存在点P,使得∠APB=90°,则m的取值范围是____.(答案:[4,6])

三、从性质定理构造圆

摘 要：高中有一种教育方法是陶冶教育法。“陶冶”的概念为董子所提出，陶冶教育法从此正式形成。什么是陶冶教育法？陶冶教育法即是对学生进行潜移默化教育的方式，教育内容与学生的社会经验、在学校的生活和其家庭生活有密切联系，与学生的综合素质也紧密结合。

在耳鼻喉科中,较为常见的一种急诊是食管异物,如果处理不及时,将会引发多种并发症,甚至对患者的生命安全造成严重威胁。在以往的检查过程中,通常采用电子胃镜、胸片、碘水造影或者食管吞钡[1]。在科学技术飞速发展的背景下,胸部CT三维重建技术得到广泛使用,其可以从客观方面判断食管并发症[2]。本次研究主要针对食管异物患者采用胸部CT三维重建与食管吞钡诊治效果进行分析,现将探究内容以如下报告形式呈现。

综上所述，在心肌梗死致心力衰竭急救过程中进行舒适护理有利于患者心功能的恢复，改善患者的心力衰竭程度，提高患者的满意度。

这实际上告诉我们可以此逆用圆的性质定理来构造圆的模型,并用之辅助解题!

夏季外界炎热潮湿，很容易导致牛出现热应激，养殖户应该高度重视夏季牛热应激防护，采取综合防控措施，有效降低牛体表温度，控制养殖环境，降低不良因素对牛身体造成的刺激，提高养殖效益。

例6 如图2在△ABC中,∠ACB=60°,点D在AB的延长线上,则CD长的最小值为___.

图2

图3

解析本题中抓住∠ACB=60°和的不变性,视顶点C在△ABC的外接圆O(半径为2)上运动,求得圆心O到边AB的距离为1,故从而有

例7 设向量a,b,c满足:〈a−c,b−c〉=60°,则|c|的最大值等于()

本文在建立房价模型时，假设住房的基本面可以由一系列经济社会变量构成，且每个城市在每个时期都对应一个反映这些经济社会变量的住房基本面价格。参考李永友(2014)[12]的模型设定，结合长三角地区的实际情况，选择人均可支配收入(hp)、年末贷款余额占GDP比重(loan)、人口规模(pop)、住房建设成本(cost)、城镇化率(urban)、土地价格(lp)和城市绿化覆盖率(green)作为基本面价格解释变量。每个城市在每个时期的住房基本面价格可通过估算模型的拟合值得出，其与同期实际房价的差值即为房价偏离。

图4

解析本题良好的解题素养体现于将相关的向量元素巧妙地整合在同一个圆的模型中:如图4,设则故顶点C、O在△ABC的外接圆上(其中外接圆的半径R=1.从而本题表面上虽为平面向量背景,但借助数学直观想象,便可发现其与上述例6有着异曲同工之妙!

2.亲虾越冬及培育 亲虾暂养于土池中，搭建加温大棚越冬，通过环保锅炉加热，期间水温保持15～18℃。至3月上旬，亲虾移入加温苗池进行产卵培育，逐渐升高水温至26～28℃，促进亲虾性腺进一步成熟。加强亲虾营养直接关系到卵和幼体质量。日常投喂罗氏沼虾专用配合饲料外，同时搭配投喂切碎的胡萝卜、南瓜等新鲜蔬菜和冰鲜鱼块，确保营养丰富、全面。日投喂量一般在4%～5%左右，投喂新鲜饲料时适当增加投喂量，越冬期间视情况适量投喂。培育期间保持环境安静，水质清新，溶氧丰富，必要时换水。池内放置PVC管和网衣作为隐蔽物，减少残杀。

综上所述，长株潭创客空间仍处于自发发展阶段，优化布局和资源共享的局面远未形成，一方面，创客空间与本地重点产业对接不足，主业特色欠缺，未能有效发挥支撑地方产业转型升级的创新驱动作用；另一方面，三座城市创新资源分布不仅不平衡，而且不平衡状况在加大，增加了劣势城市创客空间取得和使用创新资源的交易成本。上述局面从根本上导致了同质化竞争、资源使用低效、服务地方经济能力不强等突出问题。

四、从定比关系构造圆

平面内,若动点P到两个定点A,B距离之比为常数λ(λ̸=1),则动点P的轨迹是一个圆.而且这是以定比λ内分和外分线段AB的两个分点的连线为直径的圆,这种轨迹最先由古希腊数学家阿波罗尼斯发现的,因此这种圆也称为阿波罗尼斯圆,简称阿氏圆;有关阿氏圆的定义应用一直层出无穷、经久不衰!

根据视觉航标维护质量的总体要求，灯质正常就要求我们航标管理人员时刻保持灯器的正常发光，即便在恶劣天气的情况下出现异常情况就要紧急处理，确保视觉航标的正常工作，增加了航标巡检维护工作的危险性。

例4 已知m∈R,若点M为直线l1:my=−x和l2:mx=y+m−3的交点,l1和l2分别过定点A和B,则|MA|·|MB|的最大值为____.

图5

解析如图5在等腰△ABC中,设点D为腰AC的中点,注意到AB=AC=2AD,且中线BD=2.不妨暂时固定D,B两点,且以点D为原点,直线BD为x轴,则由|AB|=2|AD|可求得动点A的轨迹方程为:即点A在以为圆心、半径为的圆上运动,显然当点A到直线BD的最大距离为时,

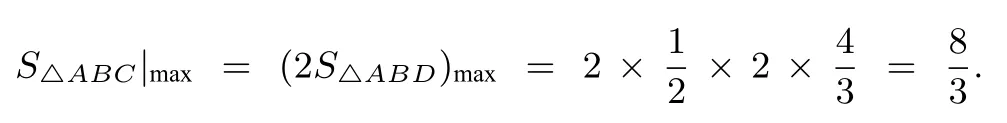
本题之所以如此建系设点,缘于由|AB|=2|AD|发现点A在某一定圆上运动,说明通过两线段的定比关系是我们构造圆的又一重要来源,也是形成直观想象素养的知识基础!

A.(0,3) B.(0,4) C.[3,+∞) D.[4,+∞)

平面内,若动点P和两个定点A,B满足∠APB=则动点P的轨迹是弦AB一侧的圆弧(不含这两个定点);

解析首先由注意到动点C在以定比内分和外分线段AB的两个分点的连线为直径的圆上运动,以此求得AB边上高的最大值为无疑比用正、余弦定理入手解三角形更为直截了当、更为直观形象,问题本质更为鲜明清晰!

例9 在三棱锥P−ABC中,AB⊥BC,AB= 6,为AC的中点,过C作BO的垂线,交BO,AB分别于R,D.若∠DPR= ∠CPR,则三棱锥P−ABC体积的最大值为____.

图6

解析凭借感官直觉,要求三棱锥P−ABC体积的最大值,关键求点P到平面ABC的最大距离d,这就要求平面PCD⊥平面PBC,且点P到直线CD的距离最大.在含30°的Rt△ABC中,易得CR=3,DR=1.在△PCD中,由PR平分∠DPC得到:根据阿氏圆的定义说明:点P在以定比3内分和外分线段CD的两个分点R,R′(RR′=3)的连线为直径的圆上运动,故于是有:

近年，材料价格波动较大，为避免由此造成承包人管理费、利润等的“水涨船高”，带动工程造价的“虚涨”，在概（估）算中对主要材料进行限价计费有一定的必要性和合理性。但对由此产生的价差处理方式，国家或行业主管部门未作统一规定，造成计价不一。有的省（市）规定列入工程单价税金之前，有的审查部门则要求列入独立费用。

点评本例充分体现:只有在充分熟知圆的各种定义、具备一定直观想象核心素养的基础上,方能在动态变幻的几何体发现或感受圆的轨迹存在.

例10 已知点P在边长为2的等边三角形ABC的内切圆上运动,则AP+2PB的最小值是____.

图7

解析根据阿氏圆定义,等边三角形ABC的内切圆可看作是到某两个定点距离之比为定值的点的轨迹.为此我们猜想存在某一定点E,使得目标式AP+2PB中AP=2PE,从而转为求2(PE+PB)的最小值.注意到中线AD的端点D恰在该内切圆上,猜想定点E应位于中线AD的中点,并且内切圆与中线AD的另一交点F点恰也满足AF=2EF,印证了△ABC的内切圆可看作是到两个定点A、E距离之比为2的点的轨迹,2(PE+PB)|min=2BE.

在△ABE中,

故AP+2PB的最小值为

点评本例逆用阿氏圆定义,将已知圆视作到某两定点距离之比为定值的点的轨迹,从而使将目标式AP+2PB巧妙转化,直观求解!

结束语笔者以为:数学定义是数学学习的起点,是数学解题的基础和推理的依据,也是发挥直观想象、形成学科素养的知识载体.由上可知,圆的定义丰富多样,圆的轨迹形成方式多样善变!只有牢固紧扣圆的各种定义,方能寻找或捕捉隐藏在数学问题中有关圆的轨迹,并利用之来化解问题.譬如某些数学问题用常规方法难以奏效或求解难度大,但若能针对问题的本质特征,恰当地构造圆的模型直观辅助分析,巧妙地运用圆的有关知识找到解题捷径,往往可以化抽象为直观、化繁杂为简捷.因此,我们学习数学定义不但要认识定义的来源及意义,理解定义的性质及相互关系,而且要在运用定义解决问题过程中追求数学核心素养的提升.