用多项式控制曲率变化的连续弯矫曲线

曾 晶，王文学，张西锋，李武红

(中国重型机械研究院股份公司，陕西 西安 710032)

0 前言

近些年来随着板坯连铸机逐渐向着精细化方向发展，人们开始对辊列中的连续弯矫曲线提出了越来越高的要求。从追求弯曲(矫直)曲线与圆弧曲线的连续到弯曲(矫直)曲线与圆弧曲线的曲率连续，甚至曲率的变化率连续，各种形式的连续弯曲(矫直)曲线不断涌现。从3次方曲线到5次方曲线，甚至到更高次的曲线被应用到连续弯曲(矫直)曲线中来。虽然这些连续弯矫曲线从数学层面实现了与圆弧曲线的光滑连接，但是却忽略了对连续弯矫曲线曲率变化的控制。因此本文从连铸坯弯曲和矫直的本质出发提出一种用多项式控制曲率变化的连续弯矫曲线的数学模型。

1 所求曲线f(S)应当满足的条件

(1)曲线f(S)的总长度为L0,S∈[0,L0]。

(2)曲线f(S)的仰角θ(S)满足θ(0)=0。

(6)曲线f(S)的曲率的导数k′(S)在[0，L0]上处处可导，如图2所示。

(7)曲线f(S)的曲率的导数k′(S)关于垂线S=0.5L0对称，如图2所示。

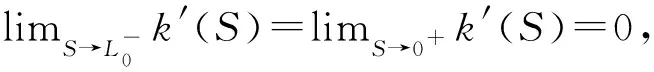
(9)曲线f(S)的曲率的导数k′(S)在S=0.5L0时取得唯一存在的极大值，如图2所示。

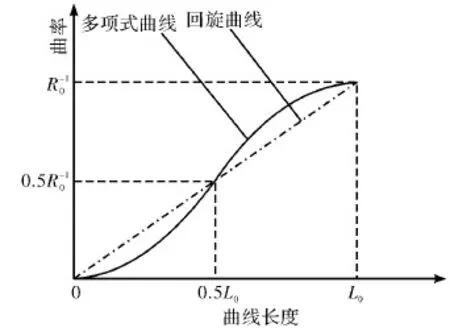
图1 曲线f(S)的曲率k(S)

图2 曲线f(S)的曲率的导数k′(S)

2 曲线的推导

基于曲线f(S)应当满足的9个条件可构建曲线f(S)的曲率的导数k′(S)如式(1)所示。

(1)

式中,a>0；b>0；n=1、2、3、4、5…。

对式(1)积分可得曲线f(S)的曲率k(S)如式(2)所示。

(2)

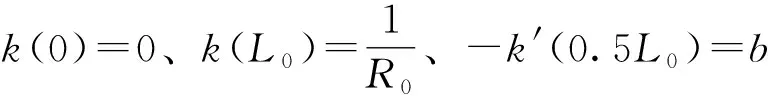
(3)

将式(3)代入式(2)得曲线f(S)的曲率k(S)如式(4)所示。

(4)

(5)

(6)

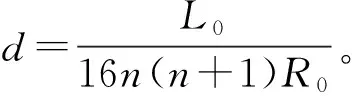
图3为曲率的微观几何意义，由此建立曲线f(S)上任意点(x，y)的横坐标x、纵坐标y关于曲线f(S)仰角θ的参数方程，如式(7)所示。

(7)

式中，K1=K2=0。

图3 曲率的微观几何意义

因为正弦函数和余弦函数可用泰勒级数展开如式(8)所示。

(8)

所以式(7)可改写为如式(9)所示。

(9)

3 曲线f(S)与回旋曲线的关系

工程应用中可根据实际情况选择m和n的值。m决定曲线的精度,m越大曲线f(S)的精度就越高；n决定曲线的类型，n越大曲线f(S)在形状上就越接近回旋曲线，随着n的增加，曲线f(S)的曲率k(S)及曲率的导数k′(S)逐渐向回旋曲线的曲率及其对应的曲率的导数逼近，如图4、图5所示。

图4 曲率k(S)的变化过程

图5 曲率的导数k′(S)的变化过程

当n→∞时，式(4)可变为如式(10)所示，式(5)可变为如式(11)所示，式(6)可变为如式(12)所示。

(10)

(11)

(12)

(13)

4 应用实例

若n=1,可得曲线f(S)的曲率k(S)、曲线f(S)的仰角θ(S)如式(14)、(15)所示。

(14)

(15)

工程应用中取式(9)的前三项就可以满足精度要求，即m=2。此时，曲线f(S)的参数表达如式(16)所示。

(16)

针对R0=8 000 mm，L0=2 500 mm的情况绘制相关曲线如图6、图7、图8、图9、图10所示。

图6 曲线f(S)

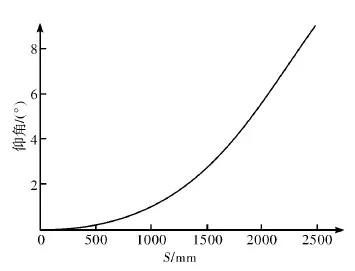
图7 曲线f(S)的仰角θ(S)

图8 曲线f(S)的曲率半径R(S)

图9 曲线f(S)的曲率k(S)

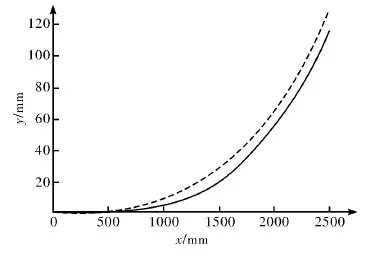
图10 曲线f(S)与回旋曲线(虚线)

5 结论

(1)连铸坯的弯曲或矫直过程的实质就是曲率的变化；只有从连续弯矫曲率的变化出发，才能较为准确地控制连铸的整个弯曲或矫直过程。本文所提出的连续弯矫曲线实际上就是让连续弯矫曲线的曲率在由1/R0逐渐地过渡到0的过程中，整个曲率的变化过程完全可控，且保证了曲率变化率的连续性，避免了因人为假定连续弯矫曲线类型而使曲线的曲率变化处于不可控状态。

(2)该模型兼顾了曲率变化率极值最小的回旋曲线模型，在n的取值较大时，连续弯矫曲线的曲率变化十分接近回旋曲线的曲率变化率，且保证了连续弯矫曲线和弧形线(直线)交接点处曲率变化率的连续性，具有更好的理论优势和实用价值。