岩质边坡地震响应振动台试验研究*
2018-08-06冯细霞姜清辉张慧超蒋金麟彭治豪江卫华
冯细霞, 姜清辉, 张慧超, 蒋金麟, 彭治豪, 江卫华
(武汉大学土木与建筑学院 武汉,430072 )
引 言
随着我国西部大开发战略的实施,许多岩土工程已建或将建在强震区,地震诱发岩质边坡破坏已成为一种最普遍和危险的地质灾害。如1999年台湾发生的集集地震造成了大量人员伤亡和巨大的经济损失[1]。2005年巴基斯坦发生的克什米尔地震造成了8万2千多人丧生[2]。2008年发生的汶川大地震诱发了将近2万个滑坡,造成了大量的人员伤亡和严重的经济损失[3]。地震诱发的岩质边坡破坏已经严重影响着人类的生命财产安全,引起了众多学者的广泛关注。
通常岩质边坡的动态响应特性和破坏机理的研究方法包括现场调查、数值模拟和物理模型试验。其中,振动台模型试验由于其成本低、周期较短、成果形象直观及对影响因素能进行重复分析,已被国内外学者广泛应用[4]。Wartman等[5]运用振动台试验调查了在地震荷载作用下边坡永久位移的机制问题,并以此评价了Newmark滑块位移方法。Wang 等[6]利用振动台试验分析了在地震作用下滑坡的启动和位移。Yang等[7]基于振动台试验调查了汶川地震滑坡的灾害现象。Zhao等[8]通过振动台试验研究了地震边坡的变形失稳机制。许强等[9]采用大型振动台试验对水平层状上硬下软和上软下硬 2 种岩性组合的岩质边坡进行了加速度动力响应特性分析。
岩质边坡的地质结构是非常复杂的,节理、断层、裂隙等普遍存在于岩体中,这些岩体非连续极大地影响着岩质边坡的变形和稳定性。考虑到岩体的非连续和地震荷载的复杂性,很难定量评价岩质边坡的动力失稳机制。Huang等[10]利用大型振动台试验调查了地震作用下反倾硬岩边坡的失稳机制。Che等[11]采用振动台试验分析了地震作用下非连续节理对高陡边坡的影响问题。然而,许多岩质边坡振动台试验只考虑了简单的地质结构(通常包括1组节理)。实际工程中,岩质边坡中存在着大量的共轭节理,而且这种节理对岩质边坡的稳定性有很大的影响。笔者基于相似理论概化了一个包含2组正交节理二维反倾边坡模型,进行振动台试验。首先,利用正交试验设计调查了相似材料的基本物理力学性质,并采用直剪试验测定了层面材料的剪切强度;其次,利用振动台试验研究了地震动参数包括加速度幅值、波频率和波类型的影响,根据试验数据和记录分析了反倾岩质边坡的动力响应特性和失稳机制。
1 模型试验相似比与相似材料设计
1.1 相似比设计
由于振动台台面尺寸、承载能力和经济等原因,模型试验往往只能根据相似理论采用缩尺模型试验。为了使试验结果尽可能模拟实际工程的性状,试验模型应尽量满足与原型的相似性。原型与物理模型相似,不仅仅要求几何形状相似,而且要求模型试验中所包含的各项物理量或主要物理量与原型相似。
在模型试验中,将原型与物理模型对应物理量的比值定义为相似系数,用Ci来表示(i为相对应的参数)。笔者基于Buckingham定理[12],根据夏颂佑等[13]对动态结构相似条件的讨论,进一步从几何条件、物理条件及运动条件相似最终确定各物理量的相似关系。根据描述物理问题最常用的基本量纲系统是质量-长度-时间(mass-length-time,简称MLT),选择密度、长度和时间作为基本物理量,三者相互独立,且包含基本量纲MLT。最终确定的相似关系如表1所示。为了能够尽可能模拟大型的实际边坡工程,长度相似关系应尽可能取得较大值。考虑到振动台尺寸的问题,本研究长度相似系数取为100,可以模拟100多米高的原型边坡。
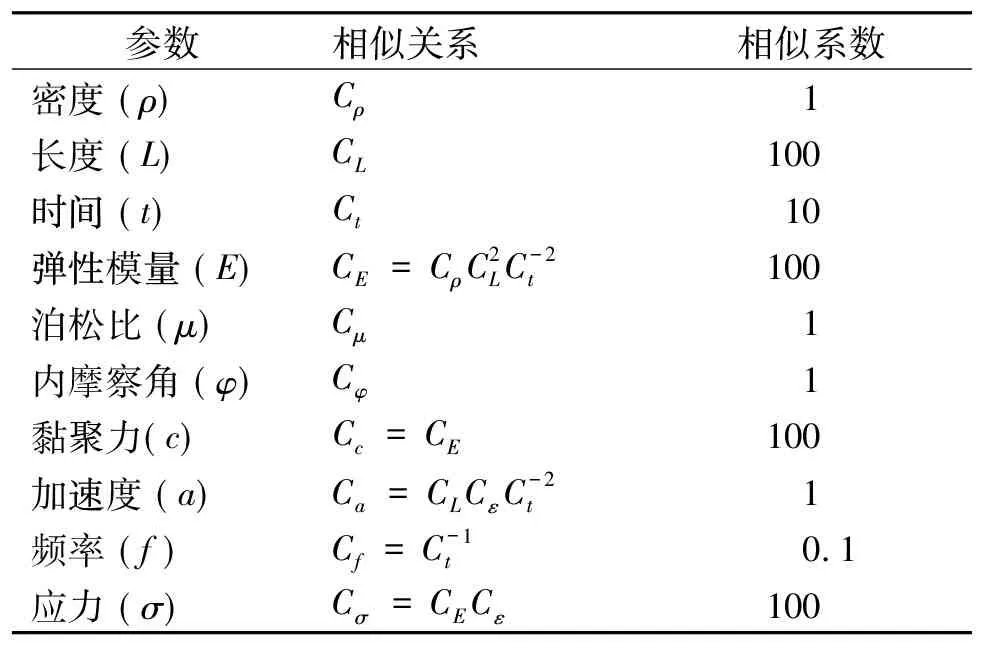
表1 振动台试验主要参数的相似率
1.2 相似材料
振动台模型试验研究层状边坡的地震响应问题,其相似材料合理的选择以及配比是试验能否成功的关键。
1.2.1 相似材料的选取
目前,国内外学者对岩土相似材料已经做了一些研究[14-16]。相似材料一般由骨料、胶结剂和辅助材料按一定配比组成,本试验选取重晶石粉(800目)、石英砂(80~120目)和重晶石粉(30~60目)作为粗细骨料,石膏作为胶结剂,甘油和水作为添加剂。其中骨料的物理化学性质稳定,重晶石粉的重度也比较大,能够满足试验材料的要求。
1.2.2 模型块体材料的配比试验
模型中各种材料的含量对组成的相似材料的物理力学性质都有一定的影响,通常需要满足相似的物理力学参数包括材料密度、弹性模量、抗压强度和抗剪强度等。为了得到合适的材料配比,往往需要进行大量的试验次数,因此试验的优化设计非常必要[17]。正交设计方法是研究多因素、多水平的一种设计方法,它是根据正交性从全面试验中挑选出部分具有代表性的点进行试验,这些点具有均匀分散和整齐可比的特点。
根据振动台模型试验的具体情况,进行相似材料配比时,本试验选取4因素3水平,选取的4影响因素为:a.石英砂和细重晶石粉的质量之比;b.粗重晶石粉与石英砂、细重晶石粉质量和之比;c.石膏与总骨料的质量之比;d.甘油的含量。确定以试件密度、单轴抗压强度、弹性模量和抗压强度作为主要考核指标。
根据相似材料的主要考核指标,需要做抗压试验和直剪试验。抗压试验需进行9组试验,每组4个抗压试样,总共36个抗压试样;同理,直剪试验总共做36个直剪试样。标准试样自然风干,待强度稳定后进行抗压试验和直剪试验测量,其结果如表2所示。
本研究目的在于研究砂岩边坡的动力响应问题,砂岩相应的物理力学参数[18-20]见表3。从表2的试验结果来看,试验2和试验3的结果与砂岩相应的物理力学参数比较相近。然而,由于甘油具有保水作用,导致试验3标准试样达到稳定的时间比试验2长。综合考虑,试验模型块体材料选取试验2的配比。
1.2.3 层面材料强度的测量
本试验研究的是反倾岩质边坡的动力响应和破坏机理,其失稳特征与机理不仅与地震波的传播密切相关,而且其内部结构面网络影响很大。因此,很有必要进行层面材料的选取及强度测量工作。
根据已有的相似材料,选取了不同配比的细重金石粉和石英砂作为层面材料,对其进行直剪试验。该直剪试验仪器是武汉大学土建院自制的试验装置,优点是能直接对本试验模型块体间的黏结材料进行强度测量,直剪试验如图1所示,结果如表4所示。最终选择了细重金石粉和石英砂的配比为1:1的材料混合物作为层面的黏结材料,可见黏结材料的强度比模型块体材料小得多。
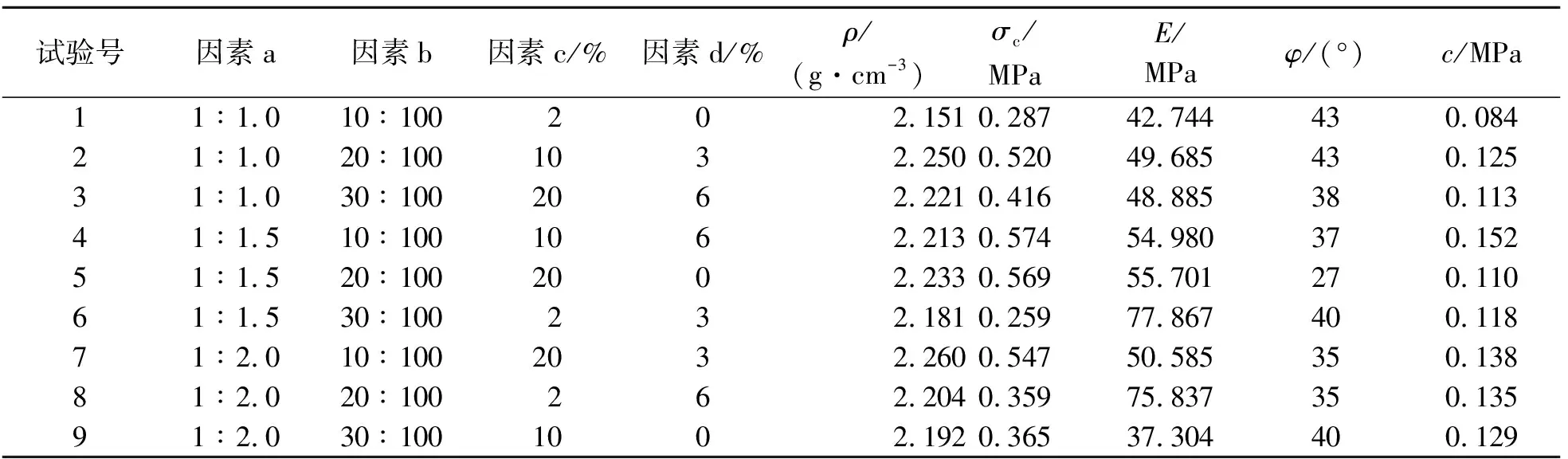
表2 模型块体材料配比正交试验及结果

表3 原型与自然砂岩相应的参数性质

图1 层面材料的直剪试验Fig.1 Direct shear tests of layered materials

表4 层面材料的配比和试验结果
2 模型试验方案
2.1 反倾边坡模型的概化
通常岩质边坡模型的振动台试验都需要采用刚性模型箱,本试验刚性模型箱的长×宽×高为1.242 m × 0.22 m × 1.2 m,前后两边为钢化有机玻璃。为了减小边界效应,模型箱的左侧优先放置20cm厚的聚苯乙烯泡沫板,底部采用模型材料浇筑一层20cm厚的垫层。
根据本试验目的和试验条件,制作了长×宽×高为1 042mm×210mm×900mm、倾角和坡角都为60°的反倾岩质边坡,如图2(a)所示。边坡模型由预制的试样块体逐层砌筑而成,试块尺寸(长×宽×高)为210mm×100mm×50mm,试样块体之间均匀地涂抹黏结材料,同层砌块和层面间用的是同一种黏结材料,完成的模型如图2(b)所示。
2.2 测量仪器的布置
边坡的加速度反应及分布规律是评价边坡地震动力响应特性的基本资料。本试验采用敏感度为1 011 mV /g的DH105E加速度传感器。为了更好地收集数据,采用的是DH5956动态信号测试和分析系统,该系统有16位A/D独立频道和较高的测量精度。所采用的程控交换的采样率能准确测量高、低频率信号,而且也支持混合过滤阻力,并能有效抑制混叠现象。为了定量地描述边坡模型的动力反应,在模型的坡表和坡顶合理布置8个加速度传感器。另外,为了获得输入加速度数据,在振动台振动方向安装了1个加速度传感器。仪器布置如图2(b)所示。

图2 反倾岩质边坡模型的概化简图和完成的传感器布置图Fig.2 Schematic diagram and photographs of complete the sensors of anti-dip slope model
2.3 地震波的输入方案
本振动台模型试验目的在于研究反倾岩质边坡在不同地震动参数作用下的动力响应特性及破坏机理。地震波采用了实际汶川安塔县地震波和不同频率的正弦波,两种波型都施加于水平方向。根据相似关系,实际的汶川波在时间轴上按10的比例进行压缩,输入压缩的0.3g水平加速度地震记录,如图3所示。为了更好地测试边坡的动力特性,试验前和每次工况输入前,施加幅值不超过0.03g的白噪声进行扫描,时间不少于60s。本试验主要设计了不同波幅值、波型和不同强度下频率的影响特征,具体的加载方案如表5所示。
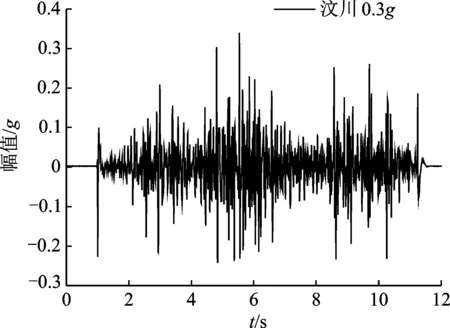
图3 振动台输入的压缩水平汶川安塔县地震波记录Fig.3 The shaking table input wave of compressed horizontal Wenchuan-Antaxian wave records
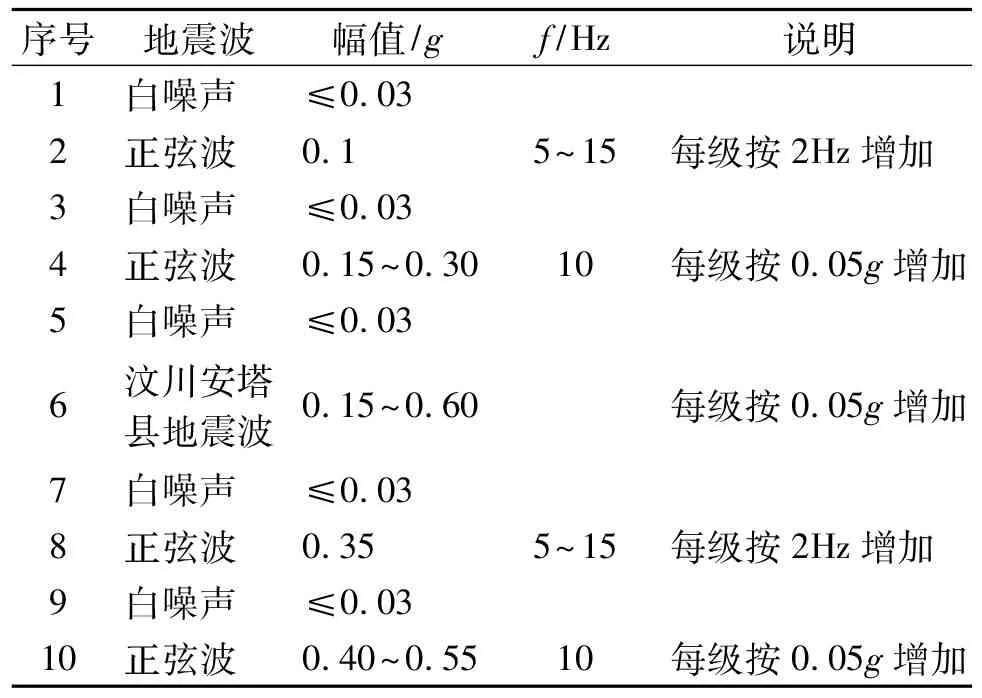
表5 边坡模型输入的地震波参数和加载方案
3 坡面质点振动加速度分布特征
3.1 坡面质点加速度分布基本特征
边坡的动力响应特性主要包括加速度、速度、 位移、 应变和应力的响应特性。加速度产生的地震惯性力是引起边坡变形和破坏的主要原因,其反应和分布规律是评价边坡地震动力响应特性的基本资料,本研究主要对加速度响应特性进行分析。为便于分析,引入量纲为1的加速度峰值(peak ground acceleration, 简称PGA) 放大系数,其定义为模型边坡内任一点的加速度响应峰值与台面实测加速度响应峰值的比值。量纲为1的相对高程,定义为边坡模型的任一测点高度与坡高的比值。

图4 反倾边坡坡面加速度曲线Fig.4 Acceleration curve of slope surface of anti-dip rock slope model
在0.2g汶川波作用下边坡坡面水平向加速度峰值随高程变化的曲线见图4。由图可知,测点A3处的加速度峰值小于0.2g,说明坡脚对加速度响应有抑制作用;测点A6处的加速度峰值大于0.2g,该处对加速度响应有放大作用。随着高程的增加,加速度峰值逐渐增大,越接近坡顶,加速度响应越强烈。通过对试验收集到的加速度数据进行分析,坡面水平加速度峰值放大系数随相对高程的增加而增大,基本呈现出非线性的放大特征,接近坡顶时加速度放大趋势显著。以输入加速度峰值为0.2g正弦波和实际汶川安塔县地震波为例,坡面水平向加速度峰值响应放大系数随相对高程变化的曲线如图5所示。由图5可以发现,在边坡4/5高度以下,加速度放大较缓慢,而超过此高度,边坡加速度放大加剧,到达坡顶时显著増大。在正弦波激振下达到了1.3,压缩10倍的实际汶川波激振下约为1.45。
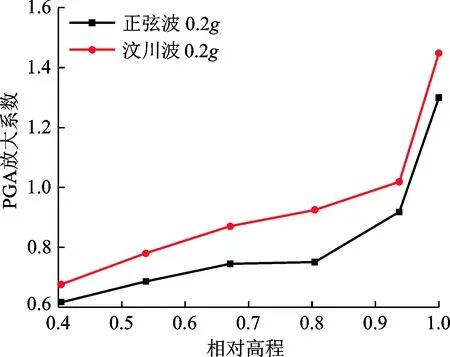
图5 反倾边坡模型加速度动力响应Fig.5 Acceleration Dynamic response of anti-dip rock slope model
3.2 地震波特征对坡面加速度分布特征影响规律
3.2.1 波型的影响
本试验采用了正弦波和实际汶川安塔县地震波两种波型,考虑了地震波型对边坡模型动力特性的影响。由图5可以看出,相比正弦波,反倾岩质边坡在实际的地震波激振下动力响应更显著。这种现象是由于实际地震波能量的不均匀分布引起的。Fan等[21]也指出地震能量的不均匀分布对边坡的动力响应有重大影响。同时图5显示,在两种波型作用下,坡面水平加速度峰值放大系数都是随相对高程的增加而增大,说明激振波型对边坡加速度响应的整体规律影响不大。
3.2.2 幅值的影响
为了研究地震波幅值对反倾边坡动力响应的影响,图6显示了反倾边坡在正弦波和实际汶川地震波不同幅值激振下加速度峰值放大系数的变化规律。图6(a)表明,在实际地震波激振下,坡面4/5坡高以下,加速度峰值放大系数随着波幅值呈现出节律性的变化,即随着幅值的增大,放大反应先减小再增大,两种变化趋势交替进行。当幅值大于0.25g时,坡面4/5坡高以上,加速度峰值放大系数随着波幅值的增大而增大。由图6(b)看出,在正弦波激振下,加速度峰值放大系数随着波幅值的增大而增大。该现象说明,波型会影响波幅值对边坡动力响应的作用。

图6 反倾岩质边坡模型在不同幅值作用下的加速度放大系数Fig.6 Acceleration amplification coefficients of anti-dip rock slope model with different amplitudes
3.2.3 频率的影响
除了波幅值和波型,波频率也是边坡动力响应的重要影响因素。笔者研究了高、低幅值作用下不同频率对边坡动力的响应规律,如图7所示。由图7(a)可知,在低幅值作用下,频率对边坡模型的动力反应不显著,加速度放大系数总体上随着频率的增大有增加的趋势,临近坡顶处反应更明显。图7(b)所示在高幅值作用下,随着频率的増长,加速度放大系数缓慢增长。当频率增大为11Hz时,峰值放大系数急剧变化,临近坡脚处首先发生突变,表明边坡该处发生了破坏。破坏处的岩体随着频率的增加,峰值放大系数迅速减小。临近坡顶处,峰值放大系数仍急剧增加,当到达15Hz的高频作用时,放大系数达到了8.07。由图7(a)和(b)所知,频率对边坡动力响应的影响跟波幅值是紧密相关的,当幅值达到一定强度时,频率对边坡动力响应有显著影响。
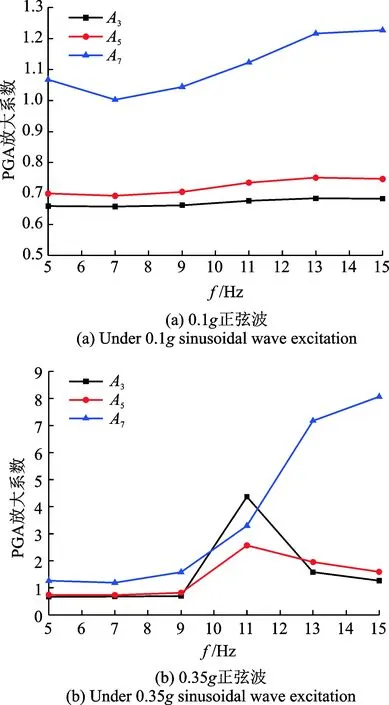
图7 反倾岩质边坡模型在不同频率作用下的加速度放大系数Fig.7 Acceleration amplification coefficients of anti-dip rock slope model with different frequencies
4 反倾边坡模型破坏特征
在试验过程中,对边坡模型的变形破坏情况进行详细的记录和拍照,以便能具体分析边坡模型的变形破坏机理。该模型在动荷载作用下的加速度响应破坏情况如图8所示,模型边坡的变形过程和最后的失稳图如图9所示。当输入0.1g的正弦波达到15Hz时,靠近坡脚处就出现了微小的裂纹,如图9所示。随着波幅值的增加,坡体靠近坡表的中上部出现了张拉裂纹。在汶川地震波不同幅值激振下,一些剪切裂纹逐渐出现在坡体靠近坡面中上部位。随着输入强度的增大,剪切裂纹逐渐扩展并贯通于张拉裂纹。边坡后缘也逐渐被拉裂,逐渐形成了陡立贯通的破裂。由图8可知,边坡模型在0.35g正弦波作用前,边坡模型加速度峰值放大系数较小,边坡变形和裂纹开度都较小。输入0.35g11Hz的正弦波后,加速度响应剧烈,模型逐渐出现大变形,裂纹开度扩大。靠近坡脚处(A3)首先出现大的变形,图7(b)加速度峰值的突变也说明了该处岩体的大变形。坡顶加速度响应更加剧烈,在0.4g正弦波作用后逐渐发生大的变形。随着输入波强度的增大,模型裂纹继续扩张贯通,到达0.5g时,边坡模型有的部位加速度响应又逐渐加强,这些部位已发生失稳破坏。直到输入0.55g的正弦波时,模型近坡表发生了整体失稳,变形破坏现象缓慢下来。通过对试验数据及整个记录的分析,靠近坡表处沿着层面出现大量的张拉裂纹,近坡面也相继出现剪切裂纹,直到与张拉裂纹贯通,形成台阶式的裂缝。随着波强度的增加,坡表发生了明显的弯曲拉裂变形(见图9)。
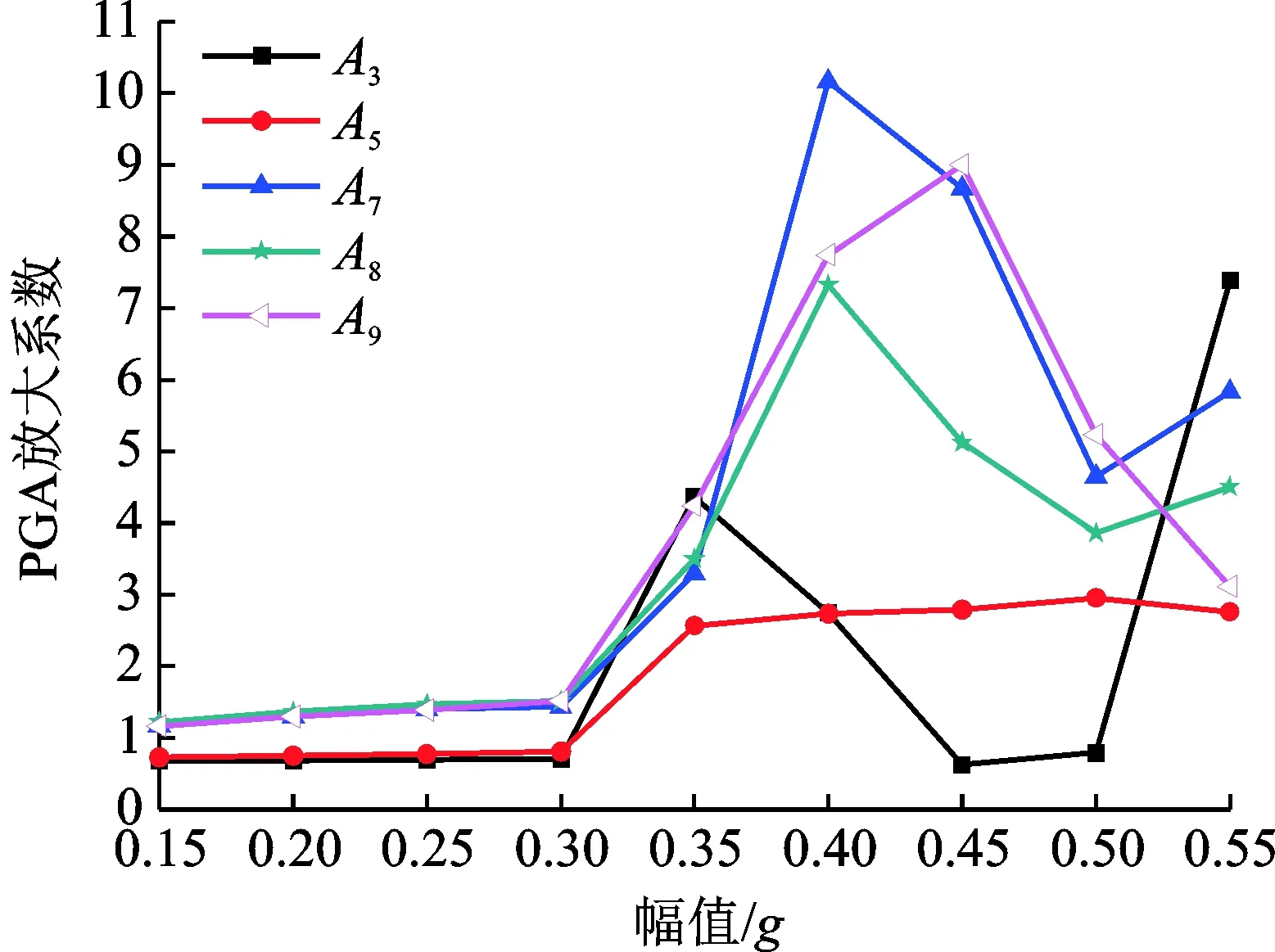
图8 反倾岩质边坡模型动力响应破坏特征Fig.8 Dynamic response deformation characteristics of anti-dip rock slope model

图9 反倾岩质边坡模型的变形特征和破坏图片Fig.9 Deformation characteristics and failure photograph of anti-dip rock slope model
5 结 论
1) 坡面水平加速度峰值放大系数随相对高程的增加而增大,基本呈现出非线性的放大特征,接近坡顶时加速度放大趋势显著。相比于标准的正弦波,反倾岩质边坡在实际地震波激振下动力响应更显著,这种现象是由于实际地震波能量的不均匀分布引起的,然而激振波型对边坡加速度响应的整体规律影响不大。
2) 地震波输入加速度幅值和频率对边坡模型的动力响应有显著影响。随着加速度幅值的增加,加速度峰值放大系数总体上呈现増大的趋势。受岩体结构和波型的影响,如在实际地震波激振下,坡面4/5坡高以下峰值放大系数随着幅值呈现出节律性的变化。随着频率的增大,加速度峰值放大系数有增大趋势,临近坡顶反应强烈。频率对边坡动力响应的影响跟幅值紧密相关,当幅值到达一定强度时,频率对边坡动力响应影响显著。
3) 包含两组节理的反倾岩质模型边坡在动力作用下主要表现为近坡表处剪切裂纹与张拉裂纹扩展,相互贯通,形成台阶式裂缝的破坏现象。坡体整体表现为沿着节理面发生弯曲拉裂的破坏模式。随着输入波强度的增大,边坡后缘也逐渐被拉裂,沿着层面逐渐形成了陡立贯通的破裂,坡脚处产生剪切挤出破坏现象。
参 考 文 献
[1] Kamai T, Wang W N, Shuzui H. The slope failure disaster induced by the Taiwan Chi-Chi earthquake of 21 september 1999 [J]. Landslide News, 2002, 13(6): 8-12.
[2] Aydan Ö. Geological and seismological aspects of Kashmir earthquake of october 8, 2005 and geotechnical evaluation of induced failures of natural and cut slopes [J]. Journal of School of Marine Science and Technology, Tokai University, 2006, 4(1): 25-44.
[3] Huang Runqiu, Li Weile. Development and distribution of geohazards triggered by the 5.12 Wenchuan earthquake in China[J].Science China Technological Sciences, 2009,52(4):810-819.
[4] 童民慧,王悦民,邱惠清. 弹性体基础变形下的岸桥车梁耦合振动[J]. 振动、测试与诊断,2017, 37(6): 1136-1140.
Tong Minhui, Wang Yuemin, Qiu Huiqing. Container crane structural elastomeric deformation under the basis of trolley boom coupling vibration response study [J]. Journal of Vibration, Measurement & Diagnosis, 2017, 37(6): 1136-1140. (in Chinese)
[5] Wartman J, Seed R B, Bray J D. Shaking table modeling of seismically induced deformations in slopes [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2005, 131(5): 610-622.
[6] Wang Kuolung, Lin Meiling. Initiation and displacement of landslide induced by earthquake: a study of shaking table model slope test [J]. Engineering Geology, 2011, 122(1/2): 106-114.
[7] Yang Changwei, Zhang Jianjing, Liu Feicheng, et al. Analysis on two typical landslide hazard phenomena in the Wenchuan earthquake by field investigations and shaking table tests [J]. International Journal of Environmental Research and Public Health, 2015, 12(8): 9181-9198.
[8] Zhao Mingsheng, Huang Dong, Cao Maosen, et al. Shaking table tests on deformation and failure mechanisms of seismic slope [J]. Jouranl of Vibroengineering, 2015, 17(1): 382-392.
[9] 许强,刘汉香,邹威,等. 斜坡加速度动力响应特性的大型振动台试验研究[J].岩石力学与工程学报,2010,29(12):2420-2428.
Xu Qiang,Liu Hanxiang,Zou Wei,et al. Study on slope dynamic responses of accelerations by large-scale shaking table test [J]. Chinese Journal of Rock Mechanics and Engineering,2010,29(12): 2420-2428. (in Chinese)
[10] Huang Runqiu, Zhao Jianjun, Ju Nengpan, et al. Analysis of an anti-dip landslide triggered by the 2008 Wenchuan earthquake in China [J]. Natural Hazards, 2013, 68(2): 1021-1039.
[11] Che Ailan, Yang Hongkai, Wang Bin, et al. Wave propagations through jointed rock masses and their effects on the stability of slopes [J]. Engineering Geology, 2016, 201(2): 45-56.
[12] Louis B.The Pi theorem of dimensional analysis [J].Archive for Rational Mechanics and Analysis, 1957,1(1): 35-45.
[13] 夏颂佑,张楚芳,张鸣岐. 动态结构模型相似条件若干问题的探讨[J].河海大学学报:自然科学版,1980(1):59-72.
Xia Songyou, Zhang Chufang, Zhang Mingzhi. Discussion on several issues of dynamic structure model similar conditions [J]. Journal of Hohai University :Nature Science Edition, 1980(1):59-72. (in Chinese)
[14] 左保成, 陈从新, 刘才华, 等. 相似材料试验研究[J]. 岩土力学, 2004, 25(11): 1805-1808.
Zuo Baocheng, Chen Congxin, Liu Caihua, et al. Research on similar material experiment [J]. Rock and Soil Mechanics, 2004, 25(11): 1805-1808. (in Chinese)
[15] 韩伯鲤, 陈霞龄, 宋一乐, 等. 岩体相似材料的研究[J]. 武汉水利电力大学学报, 1997, 30(2):6-9.
Han Boli, Chen Xialing, Song Yile. Research on similar material of rock mass [J]. Journal of Wuhan University of Hydraulic and Electric Engineering, 1997, 30(2):6-9. (in Chinese)
[16] 张强勇, 李术才, 郭小红, 等. 铁晶砂胶结新型岩土相似材料的研制及其应用[J]. 岩土力学, 2008, 29(8): 2126-2130.
Zhang Qiangyong, Li Shucai, Guo Xiaohong, et al. Research and development of new typed cementitious geotechnical similar material for iron crystal sand and its application [J]. Rock and Soil Mechanics, 2008, 29(8): 2126-2130. (in Chinese)
[17] 刘晓东,景博,石慧,等. 燃油泵故障诊断试验装置及试验方案优化设计[J]. 振动、测试与诊断,2017, 37(6): 1187-1194.
Liu Xiaodong, Jing Bo, Shi Hui, et al. Optimized design of fuel pump fault diagnosis experimental device and test program [J]. Journal of Vibration, Measurement & Diagnosis, 2017,37(6):1187-1194. (in Chinese)
[18] 叶金汉. 岩石力学参数手册[M]. 北京:水利电力出版社,1991:475-480.
[19] 邵艳,汪明武. 工程地质[M]. 武汉:武汉大学出版社,2013:88-91.
[20] 李忠建,金爱文,魏久传. 工程地质学[M]. 北京:化学工业出版社,2015:34-36.
[21] Fan Gang, Zhang Jianjing, Wu Jinbiao, et al. Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table [J]. Rock Mechanics Rock Engineering, 2016, 49(8):1-14.
