多尺度串联非线性能量阱的减振效能及阻尼连接方式研究

陈建恩， 张维兴， 刘 军， 葛为民

(1. 天津理工大学 机械工程学院 天津市先进机电系统设计与智能控制重点实验室，天津 300384；2. 天津理工大学 机电工程国家级实验教学示范中心，天津 300384)

传统的被动式线性吸振器只能在特定的频率附近才能发挥较好的减振效果，难以在复杂的工程环境中有效抑制有害振动[1-3]。非线性能量阱(nonlinear energy sink, NES)利用纯非线性弹性元件构造能量转移路径，具有振动抑制频带宽，附加质量小等优点[4-6]。NES与主结构之间能够进行靶向能量传递[7-8]，使NES可以高效和不可逆的耗散主结构的振动能量[9]。NES在减振领域的诸多优势，吸引了大量的研究者的关注。Zhang等[10]发现NES可以显著减小气动载荷作用下的复合材料层合板的振动。陈勇等[11]利用NES的宽频吸振的特性对高耸结构进行振动抑制。Yang等[12]使用NES来吸收输送流体的管道的振动能量。此外，对于梁结构的振动[13-14]，飞行器振动[15]，刀具运动过程中的振动[16]等，NES也能取得较好的减振效果。

最初的NES由单个非线性刚度元件、单个线性阻尼元件和单个质量元件组成。对传统NES进行合理的改进可以提高其减振效能和鲁棒性，串联NES是其中的一种较易实现的改进方案。Gendelman等[17]研究了主结构连接串联NES后的系统响应，发现相比单自由度NES，串联NES具有更强的靶向能量传递能力。Grinberg等[18]研究了主结构连接串联NES后的周期、准周期、混沌响应，并发现串联NES比单自由度NES的减振效能更强。Tsakirtzis等[19]研究了多自由度主结构连接多自由度NES后的复杂动力学响应。孔宪仁等[20]研究了简谐激励下两自由度NES对主结构的振动抑制效果，发现两自由度NES可以更高效的降低主结构的响应幅值。Taghipour等[21]分别研究了非线性主结构连接单自由度NES和串联NES后的系统响应，发现串联NES具有更强的鲁棒性。

现有研究主要针对由相同参数的纯立方振子构成的串联NES而进行，且NES与主结构的连接方式通常为不接地型。串联NES的构造形式对其吸振效能的影响值得探索。此外，不接地型串联NES在一定程度上克服了单自由度NES的减振效能在大幅激励下严重降低的问题，但在一些工程环境中，接地型串联NES更易实现且成本更低，因此，该类型NES是否仍具有较好的减振效能，需要进一步的研究。本文主要研究了由不同尺度纯立方振子构成的三自由度阻尼接地型NES和不接地型NES的减振效能的差异以及变化规律，并与两种单自由度NES的减振效能进行了比较。此外，对两种不同类型的串联NES中的各级纯立方振子的能量耗散能力进行了分析。

1 系统模型

单自由度线性主结构连接三自由度阻尼接地型NES和不接地型NES的力学模型分别如图1和图2所示。两种耦合系统在外激励作用下的动力学方程分别如式(1)和式(2)所示。

(1)

(2)

式中：x1，x2，x3，x4分别为主结构和三级纯非线性振子的位移；μ为主结构的阻尼系数；λ1，λ2，λ3分别为三级纯非线性振子的阻尼系数；K为主结构的线性刚度系数；k1，k2，k3分别为三级纯非线性振子的非线性刚度系数。

图1 主结构连接三自由度阻尼接地型NES的力学模型Fig.1 Mechanical model of the primary structure connected to the three-degree-of-freedom NES with grounded damping

图2 主结构连接三自由度不接地型NES的力学模型Fig.2 Mechanical model of the primary structure connected to the three-degree-of-freedom NES with ungrounded damping

对式(1)、式(2)引入如下变量

(3)

因此，式(1)、式(2)可以变换为

(4)

(5)

2 冲击激励下的系统响应

利用MATLAB软件中的龙格库塔法分别对主结构连接三自由度阻尼接地型NES和不接地型NES的动力学方程进行求解。本文选取的系统参数为

ε1=0.04，ε2=ε1/3，ε3=ε2/3,
kn1=0.3，kn2=kn1/10，kn3=kn2/10,

γ0=0.01，γ1=0.005，γ2=γ1/2，γ3=γ2/2

(6)

作用在主结构上的冲击载荷Γ(τ)为如下半正弦脉冲的形式

(7)

式中，T=0.4/π。

首先求得未连接NES与连接NES后的主结构的能量变化，通过主结构的能量变化来衡量不同的NES的减振效能的差异以及变化规律。此外，为更清晰地理解多尺度串联NES的减振效能，将其与单自由度阻尼接地型NES和不接地型NES的减振效能进行对比。为保证可比性，令单自由度NES的质量等于串联NES中的各级振子的质量之和，阻尼等于各级振子的阻尼之和，刚度与第一级NES的刚度保持相同。

主结构所具有的能量记为En，其值可以用以下表达式进行计算

(8)

定义NES对主结构的能量耗散比为

(9)

式中：η为NES对主结构的能量耗散比；E1为未连接NES时主结构所具有的能量；E2为连接NES时主结构所具有的能量。

进行计算时，要求振子的振动能够在仿真时间内完全衰减，故取仿真时间τ为0～2 000。F取值间隔为0.5，求得不同激励幅值下NES对主结构的能量耗散比，如图3所示。从图3可知，在激励幅值较低的情况下，如F=1～4时，不接地型NES的能量耗散比要远高于阻尼接地型NES，两种接地型NES对主结构几乎没有减振效果，而两种不接地型NES对主结构的能量耗散比可以达到0.33～0.50。此外，在激励幅值较低时，单自由度不接地型NES对主结构的能量耗散比要高于三自由度不接地型NES。

随着激振力幅值的进一步增加，四种NES的能量耗散比间的差距逐渐减小，之后在一定的激励幅值范围内保持相近。当NES的能量耗散比到达峰值后，再增加激振力的幅值，四种NES的能量耗散比均呈现下降趋势。值得注意的是，三自由度阻尼接地型NES的能量耗散比的下降速率要远小于另外三种NES，且其值始终保持在一个较高的数值范围。单自由度不接地型NES的能量耗散比的下降速率最大，其值会很快低于另外三种NES。此外，尽管单自由度阻尼接地型NES的能量耗散比的下降速率小于三自由度不接地型NES，但在一个相当大的激励区间内，即F=13.5～34.5，三自由度不接地型NES的能量耗散比都要高于单自由度阻尼接地型NES。

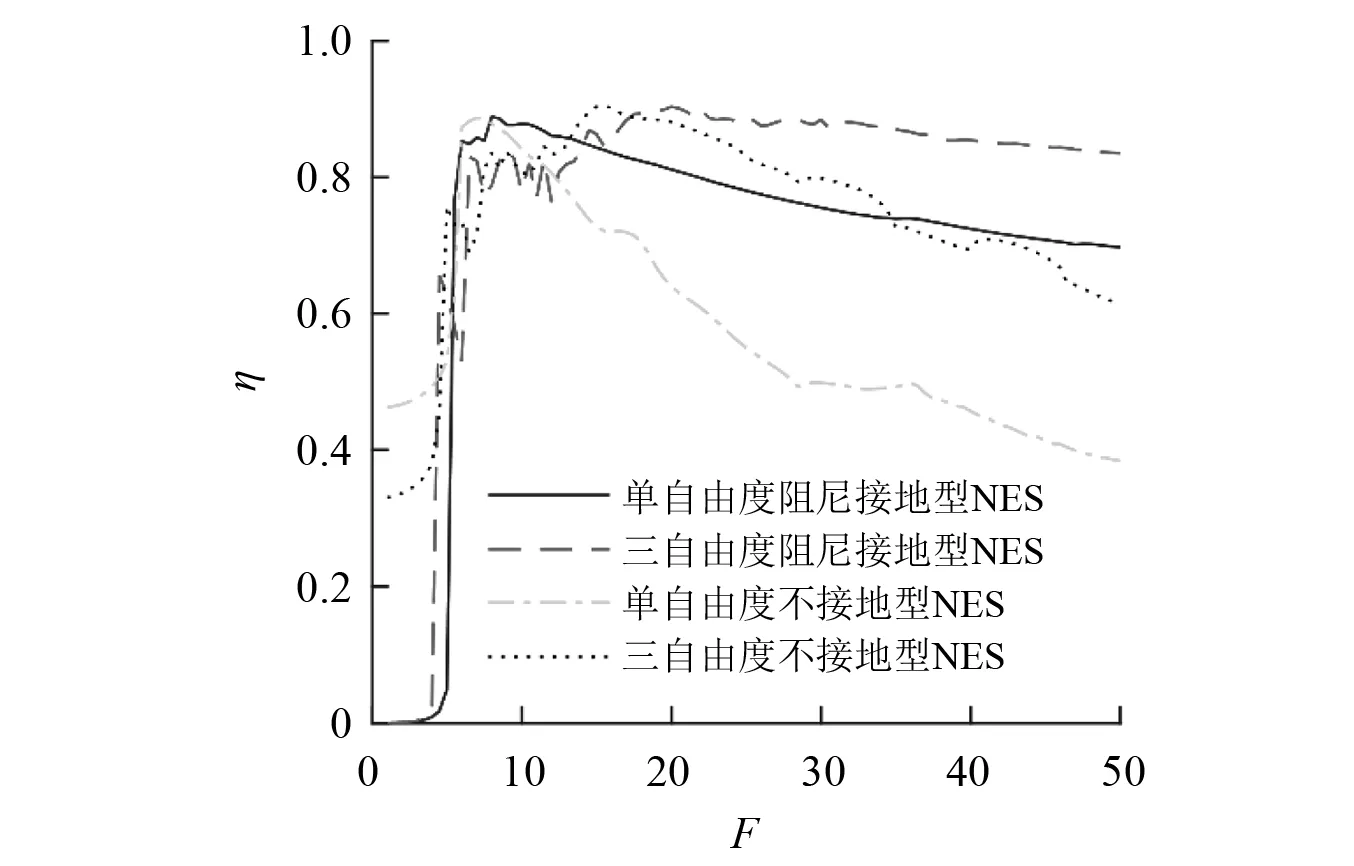
图3 NES的能量耗散比随激励幅值的变化规律Fig.3 Variations of energy dissipation ratios of the NESs with excitation amplitudes

冲击载荷下未连接NES与连接两种多尺度串联NES后主结构的波形图，如图4所示。由图4可知，冲击激励幅值F=5，F=15，F=30时，未连接NES时主结构的振动达到较低振幅(即达到初始振幅的5%以下)所需时长分别为τ=595，τ=600，τ=605，连接三自由度阻尼接地型NES时主结构到达同样的降低率时所需时间分别为τ=478，τ=278，τ=65，而连接三自由度不接地型NES时主结构到达同样的降低率所需时间分别为τ=300，τ=82，τ=75。

激励幅值为F=5，F=15时，相比于连接三自由度阻尼接地型NES的主结构，连接三自由度不接地型NES的主结构可以在更短的时间内达到较低振幅，即此时三自由度不接地型NES的减振效果好于三自由阻尼接地型NES。而当激励幅值为F=30时，三自由度阻尼接地型NES对主结构的减振效果好于三自由度不接地型NES。

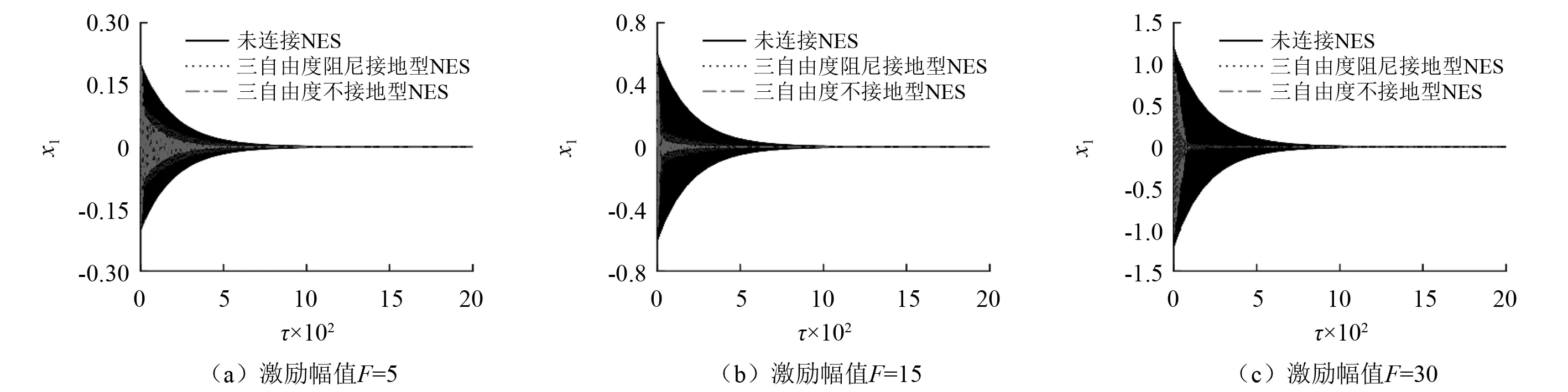
图4 不同冲击激励幅值下主结构的响应Fig.4 Responses of the primary structure under different impact amplitudes

为进一步对比分析三自由度阻尼接地型NES与不接地型NES的减振效能，令ηc，η′c分别为两种NES中各级振子的耗能比，其值可分别用式(10)、式(11)进行计算。

(10)

(11)

式中：ηc1，ηc2，ηc3分别为三自由度阻尼接地型NES中各级振子的耗能比；η′c1，η′c2，η′c3分别为三自由度不接地型NES中各级振子的耗能比。

两种串联NES中各级振子在不同激励幅值下的耗能比，如图5(a)和图5(b)所示。激励幅值较低时，即F=1～4，与图5(a)中第一级纯立方振子的耗能比接近于零不同，图5(b)中第一级振子的耗能比可以达到0.33～0.37。而随着激励幅值的持续增加，在较大的激励幅值变化范围，如图5(a)中F=11～50和图5(b)中F=8.5～50.0，第一级振子的耗能比都是最低的。

图5 不同冲击激励幅值下三级立方振子的耗能比Fig.5 The energy dissipation ratios of the three cubic oscillators under different impact amplitudes

在激励幅值较低时，第三级振子的耗能比要小于另外两级振子，而随着激励幅值的增大，第三级振子在对主结构能量耗散中发挥的作用越来越大，当冲击激励的幅值大于一定值后第三级振子的耗能比要远大于另外两级振子(见图5(a))。相似地，随着激励幅值的增大，第三级振子在对主结构能量耗散中发挥的作用也是从最小逐渐转换为最大(见图5(b))。因此，在较大的冲击载荷下，尽管质量最小，但第三级振子能够更高效地吸收并耗散主结构的振动能量，这也是多尺度串联振子的特点与优势。

3 扫频激励下的系统响应

本节对扫频激励下不同类型的NES的减振效能进行对比研究。扫频激励的幅值F=0.01时，未连接NES和连接几种不同的NES后的主结构的响应，如图6所示。图中Ω为激励频率。由图6中的五幅子图可知，未连接NES的主结构的响应幅值为0.97，连接单自由度阻尼接地型NES、单自由度不接地型NES、三自由度阻尼接地型NES、三自由度不接地型NES后主结构的响应幅值分别为0.23，0.21，0.23，0.20。扫频激励的幅值F=0.05时未连接NES和连接几种不同的NES的主结构的响应图像，如图7所示。其相应的响应幅值分别为4.87，1.83，4.36，0.61，2.90。也可发现，激励幅值较高时，连接NES的主结构在高频区间，当Ω=1.1～1.3时，会出现另一个响应波峰，但是其峰值较低(见图7(b))。

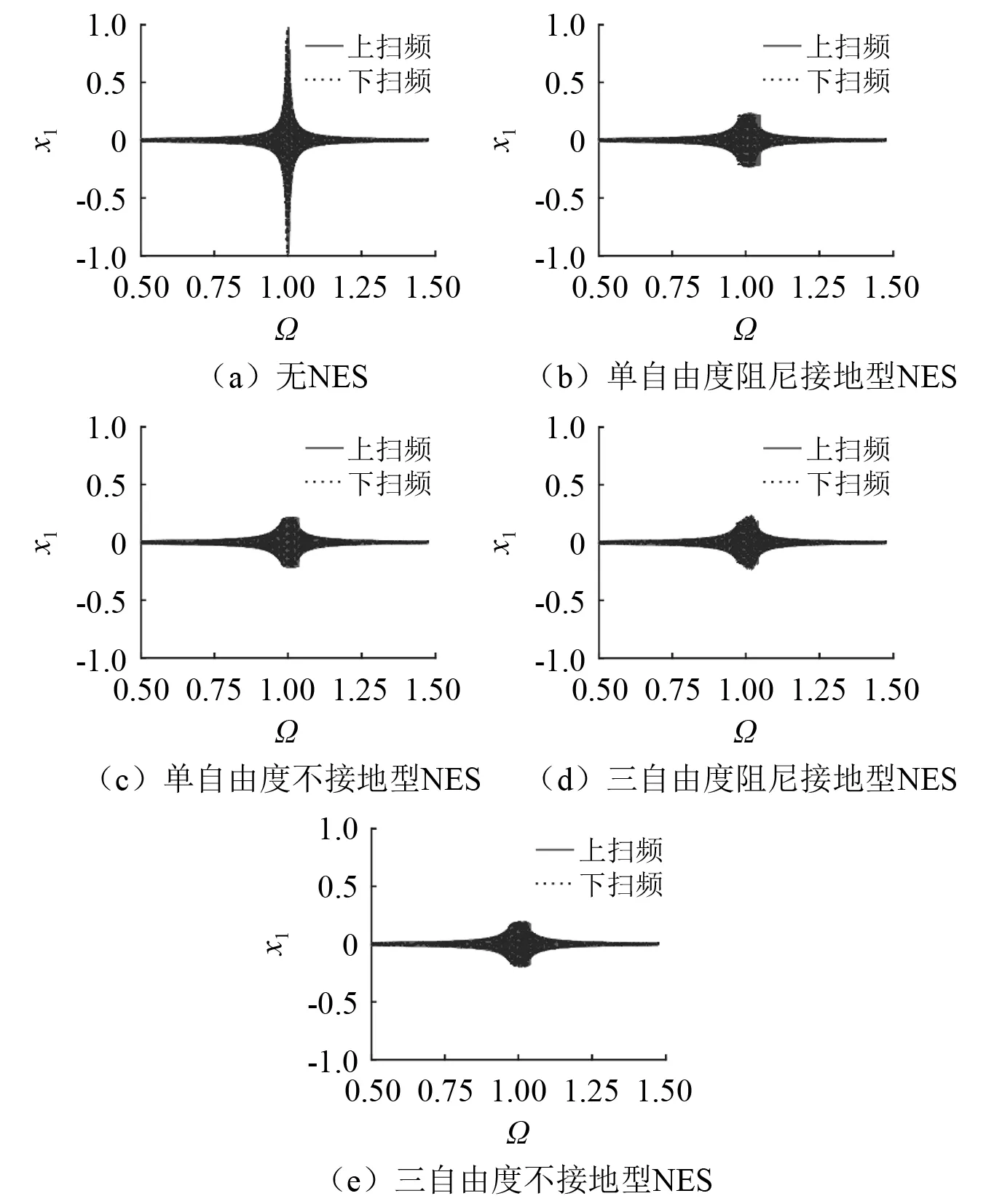
图6 扫频激励幅值F=0.01时未连接NES与连接NES后的主结构响应Fig.6 Responses of the primary structure without NES attached and connected to the NESs when the sweep excitation amplitude F=0.01

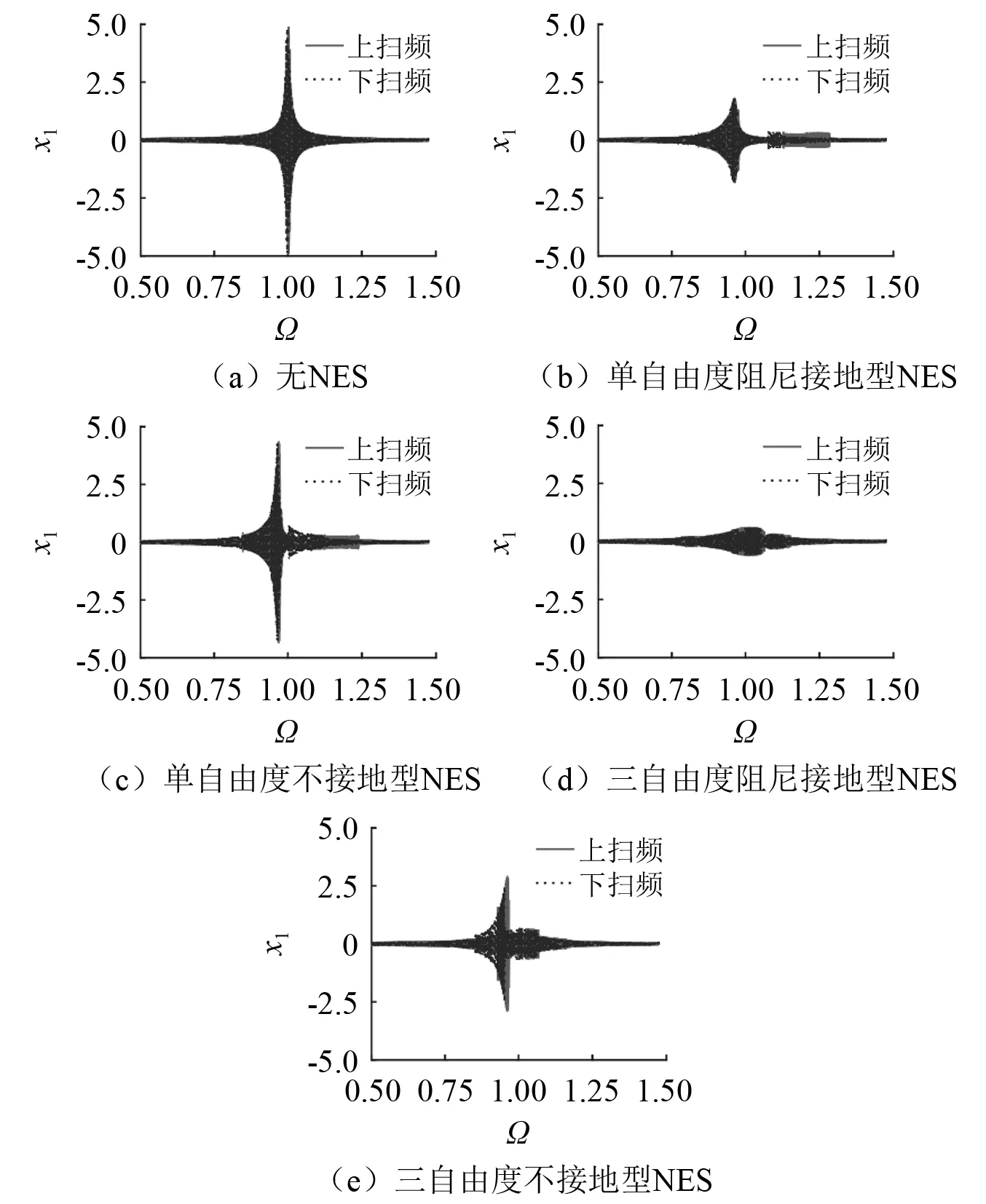
图7 扫频激励幅值F=0.05时未连接NES与连接NES后的主结构响应Fig.7 Responses of the primary structure without NES attached and connected to the NESs when the sweep excitation amplitude F=0.05

为进一步对比分析不同激励幅值下不同类型的NES对主结构响应的影响，定义NES在扫频激励下的减振效能的计算公式，如式(12)所示(一个扫频周期包含一次上扫频和一次下扫频)

(12)

式中：ηa为NES的减振效能；A1为无NES时主结构在一个扫频周期内的响应幅值；A2为连接NES时主结构在一个扫频周期内的响应幅值。

上述几种NES的减振效能的变化曲线，如图8所示。从图8可知，扫频激励幅值较低时，即F=0.001～0.003，阻尼接地型NES的减振效能要低于不接地型NES，而三自由度不接地型NES的减振效能要低于单自由度不接地型NES。随着扫频幅值的增大，这四种NES的减振效能间的差距逐渐减小，减振效能逐渐相近。之后随着扫频幅值的继续增加，各NES的减振效能陆续开始降低。值得注意的是，在扫频幅值较低时减振效能最好的单自由度不接地型NES的减振效能率先开始下降，且会在较小的激励幅值区间发生急剧降低，即F=0.019～0.025，单自由度不接地型NES的减振效能从0.86下降到了0.16。而在低扫频激励幅值时减振效能较差的三自由度阻尼接地型NES的下降趋势较小，并且可以在激励幅值较大时仍能保持较好的减振效能。

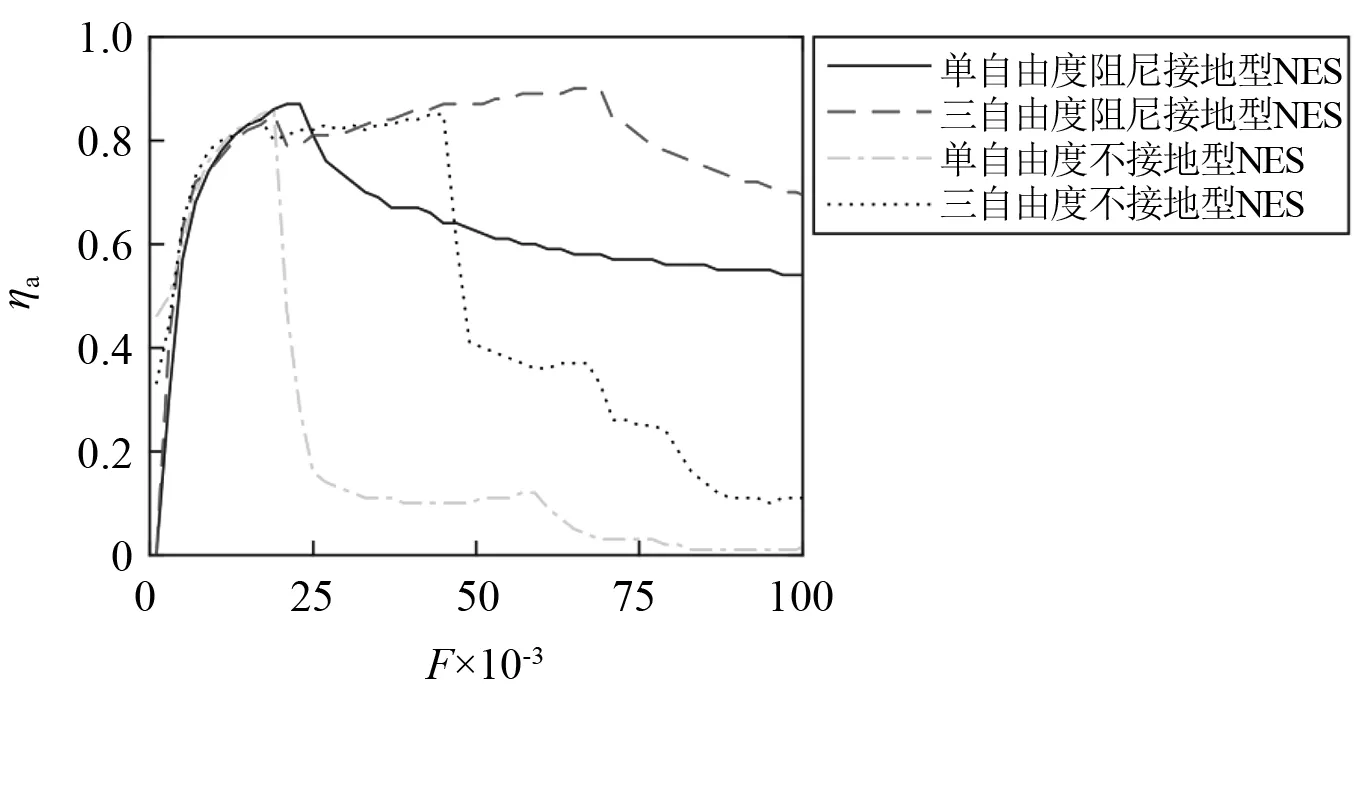
图8 各NES的减振效能随扫频激励幅值的变化情况Fig.8 Variations of the vibration reduction efficiency of different NESs with sweep excitation amplitudes

尽管在一些区间三自由度不接地型NES的减振效能要好于单自由度阻尼接地型NES，如F=0.027～0.045，但其减振效能的下降速率总体上要大于单自由度阻尼接地型NES，在一个较大的激励幅值变化范围，即F=0.047～0.100，三自由度不接地型NES的减振效能反而要远低于单自由度阻尼接地型NES(见图8)。对比图3和图8可知，在冲击和扫频激励下，四种NES的减振效能变化规律定性上一致。

令Eci和E′ci分别为三自由度阻尼接地型NES与不接地型NES中各级纯立方振子的耗能，其值可分别用式(13)、式(14)进行计算。令E表示NES总的耗能。

(13)

(14)

扫频激励下三自由度阻尼接地型NES与不接地型NES中各级振子的耗能，如图9和图10所示。对比分析图9和图10可得相同的结论，即激励幅值较低时，从图9(a)可知，当F=0.001～0.025，三个振子在主结构能量耗散中发挥的作用基本相同；而随着扫频激励幅值的持续增加，在扫频激励幅值变化的较大范围内；当F=0.041～0.100，第三级振子在主结构能量耗散中发挥的作用最大，耗能最高，而第一级振子在对主结构能量耗散中发挥的作用最小，耗能最低。不同的是，随着激励幅值的增加。图10中三个振子间的耗能的差距会基本呈现越来越大的趋势，而图9中三个振子间的耗能的差距会逐渐保持相同。

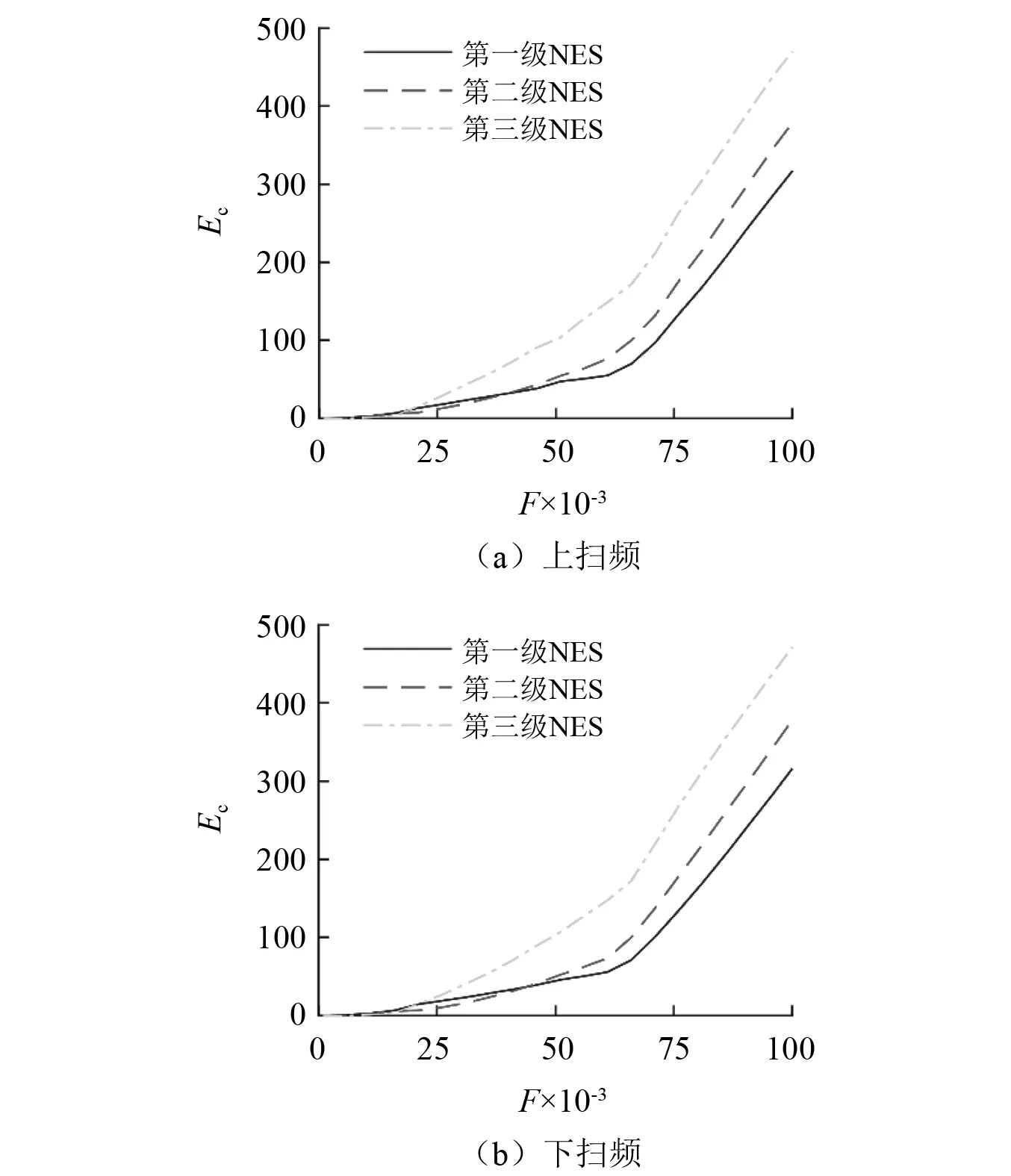
图9 三自由度阻尼接地型NES的各级纯立方振子的耗能Fig.9 Energy consumption of purely cubic oscillators of the three-degree-of-freedom NES with grounded damping

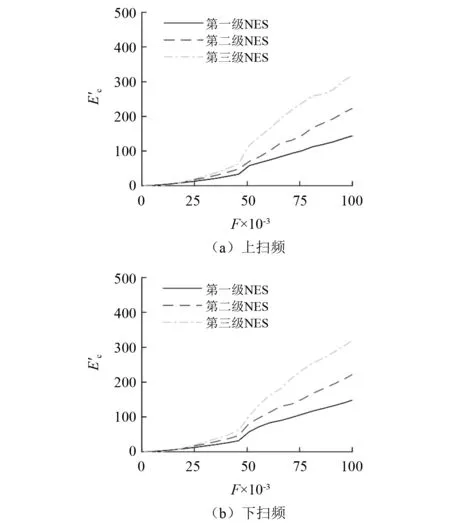
图10 三自由度不接地型NES的各级纯立方振子的耗能Fig.10 Energy consumption of purely cubic oscillators of the three-degree-of-freedom NES with ungrounded damping

上扫频和下扫频过程中的上述几种NES的总耗能变化曲线，如图11所示。由图11中的两幅子图可知，无论上扫频还是下扫频，在激励幅值较低时，当F=0.001～0.025，这几种NES的耗能相差较小。随着激励幅值的进一步增大；当F=0.025～0.073，单自由度阻尼接地型NES的耗能最大，而单自由度不接地型NES的耗能最小；持续增加激振力的幅值，当F=0.073～0.100，三自由度阻尼接地型NES的耗能最大，而单自由度不接地型NES的耗能依然最小(见图11(b))。

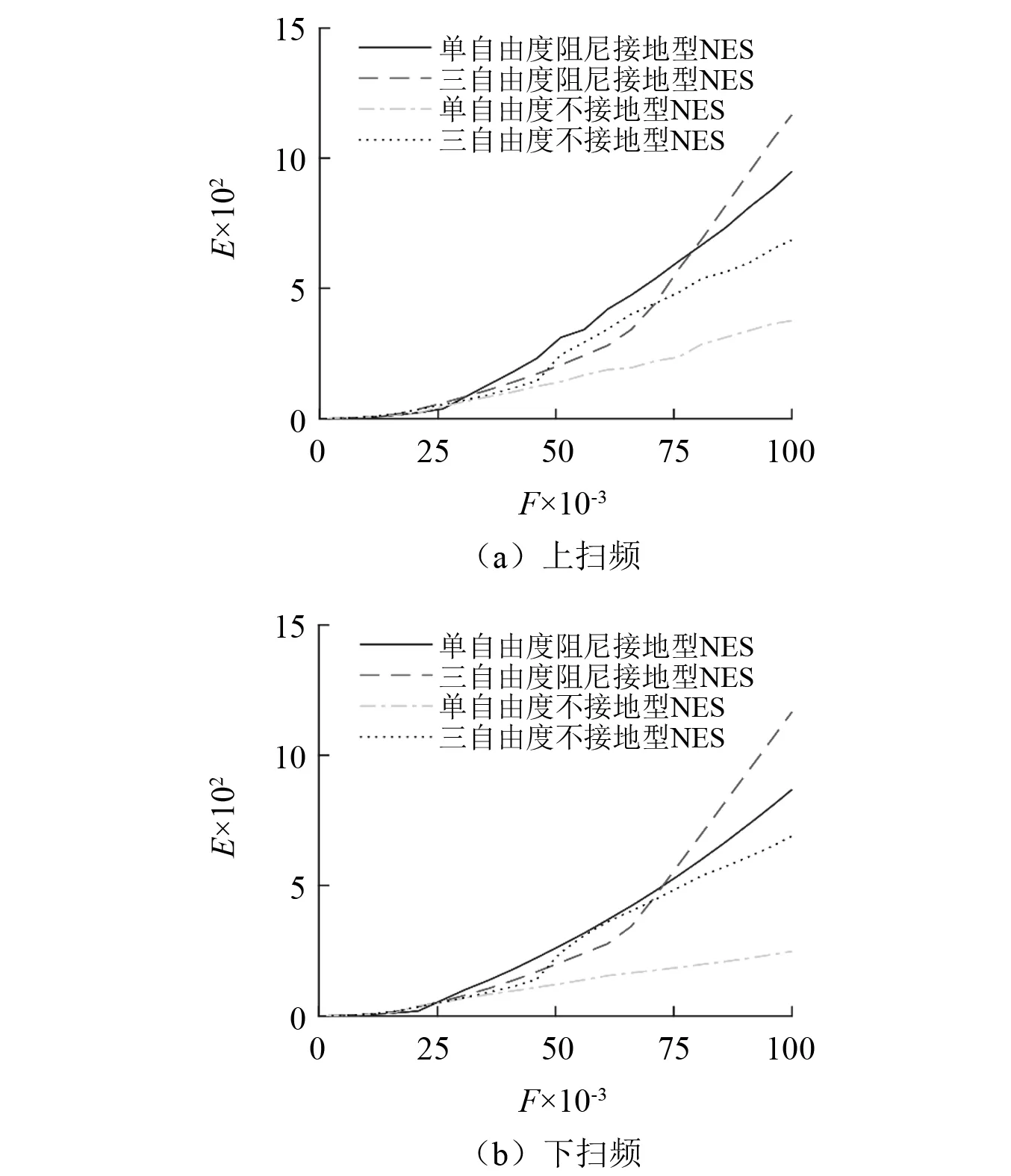
图11 不同扫频激励幅值下各NES的耗能Fig.11 Energy consumption of the NESs with different sweep excitation amplitudes

4 结 论

对比研究了冲击和扫频激励下不同类型NES的减振效能的差异和随激励增大的变化规律，并分析了串联NES中各级纯立方振子的能量耗散能力的不同。主要结论如下：

冲击和扫频激励幅值较低时，不接地型NES的减振效能要高于阻尼接地型NES，单自由度不接地型NES对主结构的减振效能高于三自由度不接地型NES，随着激振力幅值的进一步增加，四种NES的能量耗散比间的差距逐渐减小，之后在一定的激励幅值范围内保持相近。随着激励幅值的继续增加，在较宽的激励幅值变化范围内，三自由度阻尼接地型NES能够在较大激励幅值范围内始终能够保持较好的减振效能。

两种串联NES的各级纯立方振子在能量耗散中发挥的作用均随激励幅值的增加而变化，当激励幅值较大时，质量最小的第三级振子反而能够最大程度的消耗能量。此外，在不同的激励类型下，四种NES的减振效能的变化规律在定性上一致。所不同的是，在扫频激励下，两种不接地型NES的效能会发生跳跃式下降，接地型NES则没有发生这种现象。