薄膜型声学超材料的低频吸收性能研究

曹卫锋， 白鸿柏， 朱 庆

(1. 榆林学院 能源工程学院，陕西 榆林 719000; 2. 军械工程学院 车辆与电气工程系，石家庄 050003)

超材料对电磁波可以进行有效吸收的概念，是1964年前苏联科学家Veselago最先提出的。他明确表示除了传统意义上的双正(正质量、正刚度)材料，还应该包括单负或双负的材料。因此，对于负有效质量和负有效刚度特性的声波超材料，开始被人们关注。

无论是王刚等[1]提出的局域共振形式的声子晶体，还是Mei等[2-4]提出的暗声学超材料，最主要的吸收形式都是由软、硬相介质作用而产生的局域振动与声波辐射模式之间的弱耦合。该局域振动形式符合质量-弹簧系统构成的振动吸收器，基于振动吸收器原理，绝大多数声波超材料结构可以近似看作集中质量与理想弹簧相互作用的振动系统[5-6]。对于一维超材料梁结构，可看作由胞元周期性排列构成的、具有双负特性的声学超材料模型(如图1所示)。同时，超材料结构可以产生有效带隙，很大程度上对材料结构中行波的传播进行了有效的控制。

根据带有双负特性的一维超材料梁结构[7]，本文提出一种薄膜超材料结构，该结构实现了以‘小尺寸控制大波长’，对于数百赫兹的低频声波可以很好地吸收。并且从理论上解释了负有效质量。利用有限元软件分析了子结构胞元和薄膜超材料的振动形态，探讨了胞元结构与入射声波的耦合形式，分析了在一段频率范围内声波辐射模式与薄膜结构的共振特性存在等效关系，同时，对不同刚度的薄膜材料进行仿真分析，比较振动形态对声波吸收形式的差异。最后通过不同薄膜的薄膜材料对低频声波吸收效果和结构胞元与周期结构的吸收特性进行试验研究。

1 结构设计

根据超材料梁的双负材料属性，基于质量-弹簧谐振系统的吸收器原理，可将超材料梁的理论模型简化为图1所示。其中，集中质量与理想弹簧作用在一维梁结构上，可看作n个胞元结构进行周期性排列，这种谐振子形式对声波具有很好的吸收效果，因此，利用振动吸收器原理，本文建立一种二维薄膜超材料结构，图2为结构的平面图。

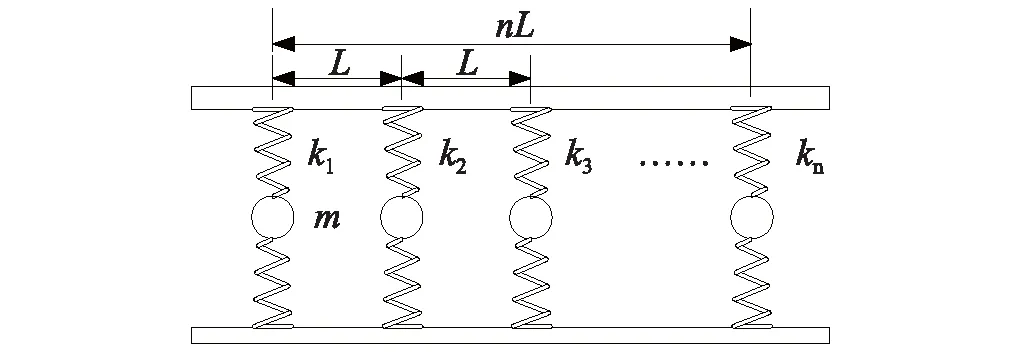
图1 超材料梁的振动系统Fig.1 The system of metamaterial beam

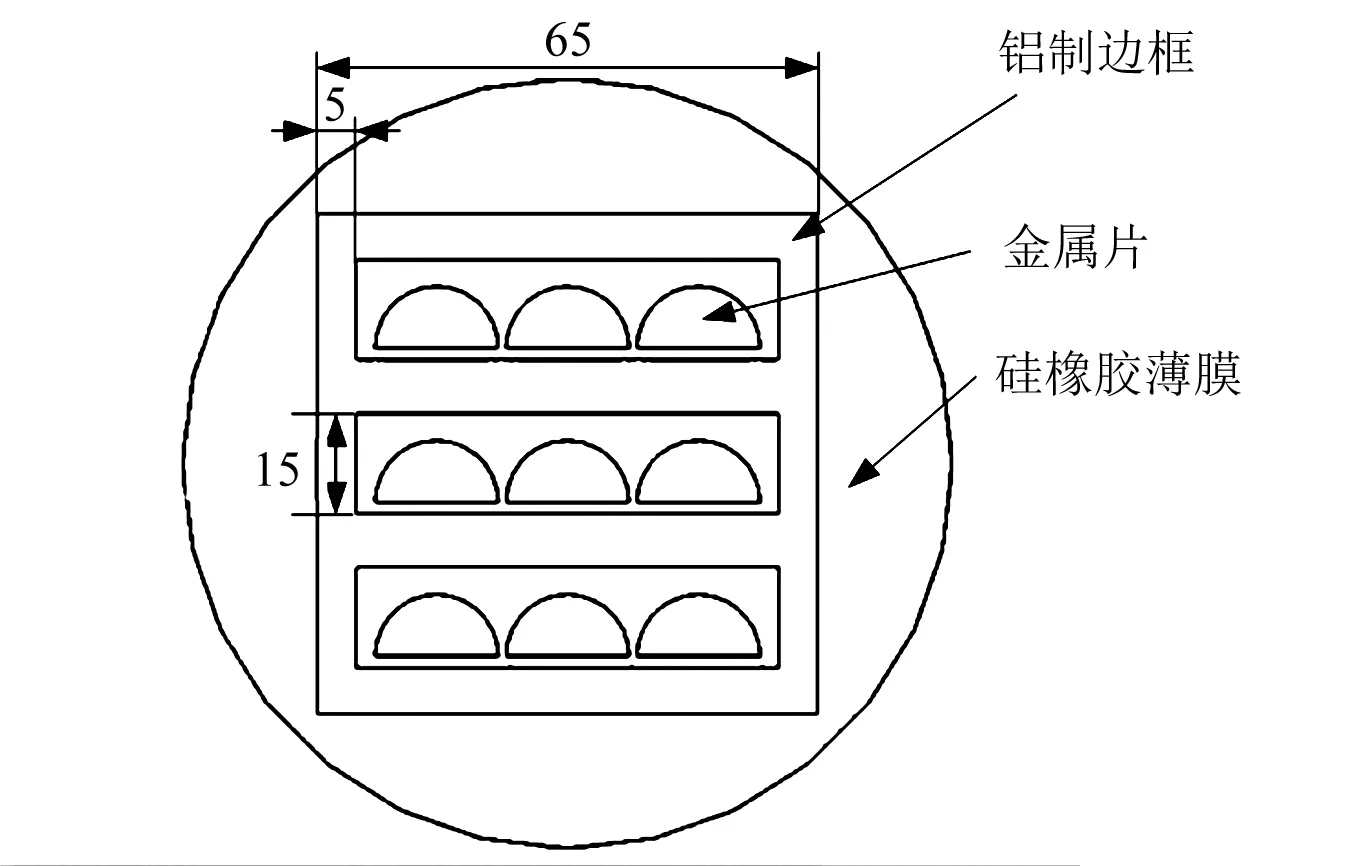
图2 薄膜超材料平面图(mm)Fig.2 Metamaterial membrane graph(mm)

首先，在硅橡胶薄膜两侧镶嵌长、宽为65 mm的铝制边框，金属片水平镶嵌到薄膜表面，并在薄膜四周镶嵌PVC硬质边框。为了方便研究，取薄膜超材料中金属片对薄膜约束的一部分进行分析，如图3所示。

图3 镶嵌薄膜结构振动系统(mm)Fig.3 The system of elastic membrane decorated with relatively rigid platelets(mm)

图3表示出金属片与薄膜之间的位置关系，其中薄膜的弹性性能表示为理想弹簧，采用胶黏剂将厚度1 mm，半径为8 mm的半圆金属片镶嵌到薄膜表面，整个系统可看作理想的质量-弹簧谐振子系统，这种共振结构使材料具有负有效质量及负有效刚度，下面根据质量-弹簧谐振子系统建立两种理论模型，分别讨论其共振机理。

2负质量的材料属性

根据薄膜超材料的振动特性及共振机理，定义了该结构中谐振单元形式(单个金属片与作用薄膜面积形成的质量-弹簧微结构)，因为金属片为刚性介质，对声波存在较强的反射作用，这里仅考虑薄膜的弹性系统对金属片的牵引力作用，构建如图4所示的胞元质量-弹簧振动系统。该系统受到声波F1=Paejω0t激励作用，其中m1、m2分别为单元薄膜、单个金属片的质量。薄膜、金属片的位移u1、u2均表示为简谐形式，薄膜的弹性性能表示为金属片与薄膜之间的弹性系统k1。

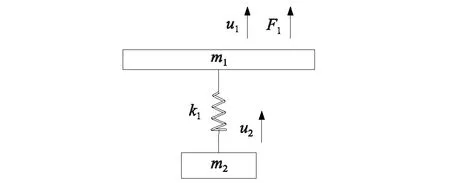
图4 质量-弹簧振动系统Fig.4 The system of mass-spring vibration

根据如图4所示的质量-弹簧系统，建立振动微分方程如下

(1)

通过计算，可得式(1)的解为u1=a1ejω0t、u2=a2ejω0t，其中a1、a2为常数。对公式(1)进行整理得

(2)

通过联立式(1)、(2)，可得关系式

(3)

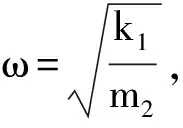
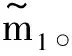
(4)

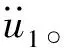
此时单自由度的微分方程可表示为

(5)

将负的有效质量代入到方程(5)中，可以得到

(6)

很明显式(6)中等式左侧部分小于0，作用在薄膜上的牵引力弹簧作用k1u1大于简谐波的激励作用F1，这也说明了薄膜有效质量为负值的原因。

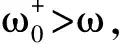
为了约束薄膜反共振的波动形式，增强薄膜的共振特性，通过附加质量约束，在一定程度上将入射的声波以局域共振的方式衰减，使结构具有更宽的共振带隙，其声波衰减形式表现为局域共振与声波辐射模式之间的耦合。

3 数值模拟分析

3.1 薄膜超材料的振动形态

为了便于分析薄膜超材料的振动形态，设置薄膜、铝制边框四周为固定约束，并在模拟时设置入射、出射端辐射边界条件，网格划分为自由剖分四面体网格，如图5所示。

为了分析不同声波频率与薄膜结构的耦合程度，在10～1 000 Hz低频范围内进行数值模拟，可以得到任意频率下的振动形态。同时，考虑到薄膜与金属片的振动形式对声波频率具有选择性吸收的特性点，且根据设定步长34，选取180 Hz、282 Hz、350 Hz及792 Hz四个频率，得到四种入射声波与薄膜结构的耦合情况，如图6所示。

图6 振动形态Fig.6 the mode of vibration

分析图6可知，在四个频率下声波的激励作用可以得到薄膜结构不同的振动形态。图6(a)是入射声波与薄膜结构的中央部分发生强耦合作用，镶嵌在薄膜表面上的金属片受薄膜弹性作用发生强烈的“拍动”，即声波经过薄膜结构时，声波以全反射的形式反射回来。图6(b)、(c)是存在个别谐振单元与入射声波发生强耦合作用，部分声波能量被质量-弹簧系统的共振特性所吸收，吸收声波的薄膜结构表现为谐振单元与薄膜之间没有发生相对位移变化。图6(d)说明了金属片与薄膜形成的质量-弹簧系统的共振特性几乎全部用于声波能量的吸收，仅有一少部分声波与周围薄膜存在耦合作用，该频率附近的薄膜结构振动形态对入射声波可以很好地进行抑制传播，声波会以零反射的形式被吸收。

3.2 薄膜与薄膜超材料的位移分析

在外界声波激励作用下，当四周固支薄膜留有一定距离的背衬腔时，薄膜受到背腔后空气弹簧的影响，具有一定的共振特性，但吸收效果不明显。

为了进一步分析金属片对薄膜约束作用，选取单层薄膜与薄膜超材料中心点位置，设置声压载荷为122 Pa，得到两组随频率变化的法向位移曲线，如图10所示。

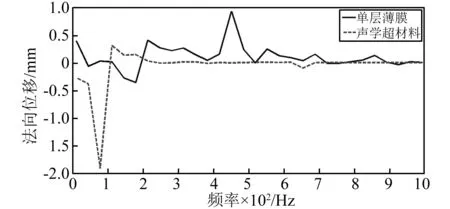
图7 法向位移曲线Fig.7 The vertical displacement curve

图7中虚线表示声学超材料，实线表示单层薄膜。对于薄膜超材料来说，当频率达到112 Hz时，中心点法向位移由最初的负值(z轴负方向)转变为正值(z轴正方向)。同时在112 Hz之后，中心点的法向位移趋于稳定，且逐渐趋于0。同薄膜超材料对比可知，当单层薄膜受入射声波激励作用时，薄膜中心点在平衡位置处存在较大的波动，与此同时，大部分的声波都以反射的形式存在，仅有一少部分声波能量进行阻尼损耗而被吸收。

也正是在薄膜表面镶嵌了多个周期形式的结构胞元，每个结构胞元都可以看作单个质量-弹簧的局域共振作用，这种质量-弹簧系统将薄膜与声波之间的反射形式进行削弱，同时，金属片对薄膜在平衡位置处的法向位移进行了约束。总的来说，薄膜对金属片的弹性力作用与入射声波的能量进行相互抵消，使得入射声波能量进行很好地吸收。

3.3 子结构胞元的振动形态

为了进一步分析薄膜结构中金属片与硅橡胶薄膜之间的作用，将图2所示的声学超材料中单个金属片与单元薄膜的组合形式看作结构胞元，按照平面结构的尺寸计算，取面积为20 mm×15 mm的硅橡胶薄膜定义为单元薄膜，在其表面上镶嵌单个金属片，得到结构胞元，如图8所示。

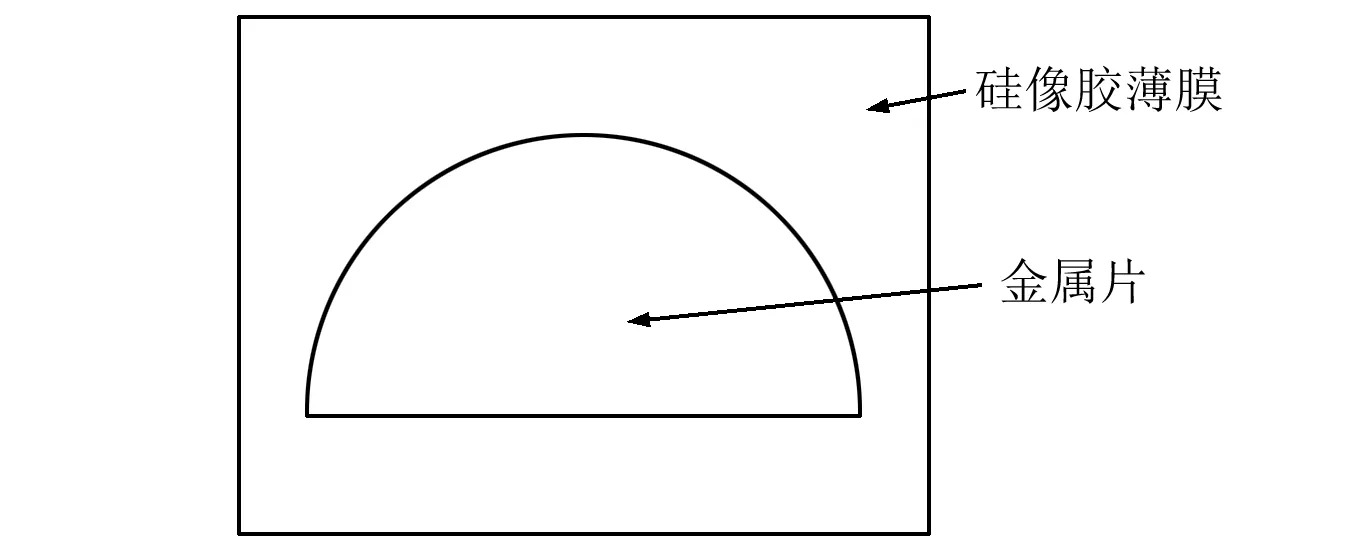
图8 子结构胞元Fig.8 The substructure cell

为了对结构胞元的振动形态进行精确分析，设定频率步长为12，在10～1 000 Hz范围进行频域求解。图9是6个频率点对应单个金属片与薄膜之间的振动形态，其中，不同频率对应的振动形态对声波的吸收效果不同，这进一步证明了结构胞元对声波频率的选择吸收性。

图9 振动形态Fig.9 The vibration mode

通过比较图9(a)～(f)的振动形态，可以发现，图(a)、(b)、(c)的振动形态中金属片振动形式与硅橡胶薄膜振动形式为同相位，即质量-弹簧系统形成的振动形式为声学模式，透过该结构胞元的声波能量会反射回来，薄膜提供给金属片的弹性作用不能对入射声波能量进行吸收，耦合形式加强。图(d)、(e)、(f)的振动形态均表现出金属片对薄膜法向位移的约束作用。其中，图(d)的振动形态中金属片受薄膜弹性力作用与硅橡胶薄膜位移方向相反，即质量-弹簧系统形成的振动形式为光学模式，入射声波的能量开始被质量-弹簧系统吸收，声波的传播形式被结构胞元的振动形式所抑制。当达到214 Hz时，入射声波能量大部分被结构胞元的振动形式所吸收，只有一少部分声波与薄膜存在耦合作用，其声波的反射形式很少。图(f)的振动形态表示为金属片与薄膜之间的相对法向位移没有变化，入射声波能量被结构胞元振动形式完全吸收，进一步说明了在该频率附近的声波与薄膜结构的共振特性吻合较好，此时，声波以零反射的形式被吸收。

通过在四周固支约束的薄膜表面附加金属片质量，进一步增强了薄膜的约束形式，使薄膜结构在某一段频率范围内可以选择性的吸收声波，具体表现为在该频段金属片与薄膜之间的相对位移几乎为零，声波能量被质量-弹簧系统的振动形式所吸收。金属片受薄膜作用产生的振动形式与一段频率范围内声波进行吻合时，吸收效果最佳，这也为后文试验中吸收峰值接近1进行很好的证明。

当薄膜的物理属性被重新定义时，取杨氏模量E=4×109Pa，泊松比μ=0.44，质量密度ρ=1 400 kg/m3(PET薄膜的物理性能满足该材料属性)。设定频率步长为12，在10～1 000 Hz范围进行频域求解，选取图9所示振动形态下的6个频率点，并且在相同频率步长和相同频率范围内进行频域求解，最终得到单个金属片与PET薄膜之间的振动形态，如图10所示。

通过比较硅橡胶薄膜与PET薄膜两种材料属性在相同频率下的振动形态。可以发现，单个金属片与PET薄膜形成的子结构单元在10～1 000 Hz范围内只有一个振动形态。随着频率的变化，金属片的运动方向和硅橡胶薄膜的运动方向始终保持同相位，且位移发生微小变化。由于两种薄膜的材料属性不同，可以得到不同刚度薄膜对声波吸收的差异。

再分析相同质量的金属片镶嵌在不同刚度薄膜上的吸收效果。因为金属片和PET薄膜组成的声学材料具有相同的振动形态，即质量-弹簧系统形成的局域共振形式为声学模式，经过声学超材料的声波能量会反射回来，几乎没有声波能量被二者的振动形式所局域掉，同时，薄膜提供给金属片的弹性作用不能与入射声波能量进行抵消，耦合形式为强耦合。这也为后文这两种不同刚度薄膜对低频声波吸收效果的分析奠定理论基础。

图10 振动形态Fig.10 Vibration mode

正是由于两种结构胞元中薄膜设置的材料属性(刚度特性)不同，导致两种结构胞元对低频声波的吸收存在差异，同时，为后文这两种不同薄膜刚度的声学超材料对低频声波吸收效果分析奠定仿真试验基础。

4 试验研究

通过对不同薄膜刚度的声学材料进行试验和结构胞元与周期结构的吸收特性分析，分析了质量-弹簧系统对低频声波吸收的重要性。

4.1 两种不同刚度薄膜对声波吸收的影响

本文选择聚对苯二甲酸乙二酯(PET)薄膜和硅橡胶薄膜作为试验材料，其中聚对苯二甲酸乙二酯(PET)薄膜是一种聚酯薄膜，密度大约为1.4 g/cm3，具有高抗张强度和高抗冲击性能的特点；硅橡胶薄膜是以聚硅氧烷为主链，具有一系列独特性能的特种橡胶，密度大约为0.98 g/cm3，薄膜厚度在0.05～0.25 mm之间(本文试验选择的是0.2 mm的硅橡胶薄膜)，具有一定的弹性、强度和柔软性。

在刚度不同的薄膜表面上镶嵌相同的集中质量，可以形成不同的质量-弹簧共振形式。首先，取PET薄膜和硅橡胶薄膜两种不同刚性的薄膜进行声学测试，图11是实验系统图，其中左侧为试验元件的连接图，右侧为低频试验测试的阻抗管，入射声波设置为白噪声。试验系统的频率测试范围是50 Hz～1 kHz，测量系统是由AWA8551型阻抗管、AWA6290M型信号发生器和AWA5871型功率放大器等器件组成。将试件放到直径为100 mm的阻抗管中，通过拉动阻抗管中滑杆的位置来控制试件后空气腔的距离，试验时，取空腔厚度为30 mm。

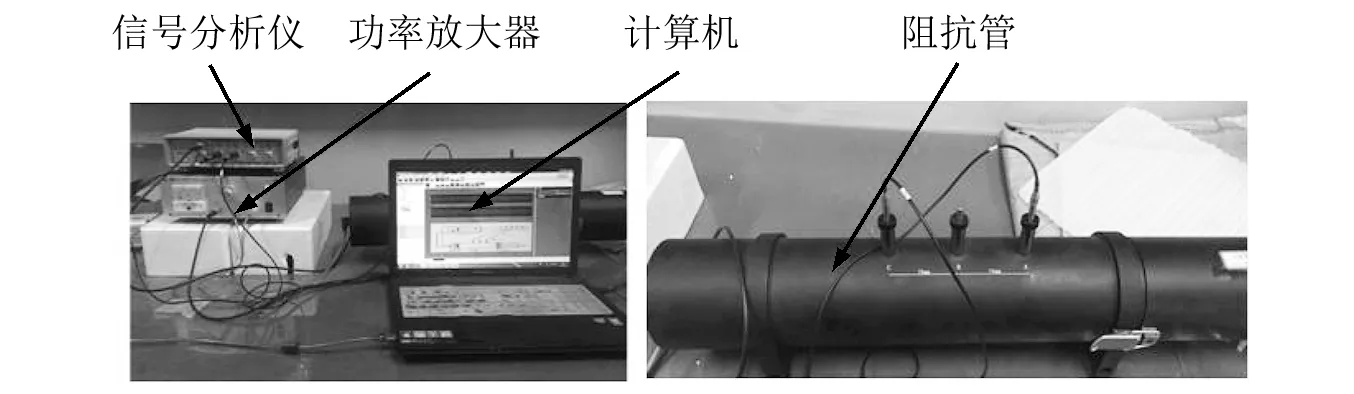
图11 实验系统Fig.11 the system of experiment

得到两种薄膜对低频声波吸收的情况，如图12所示。

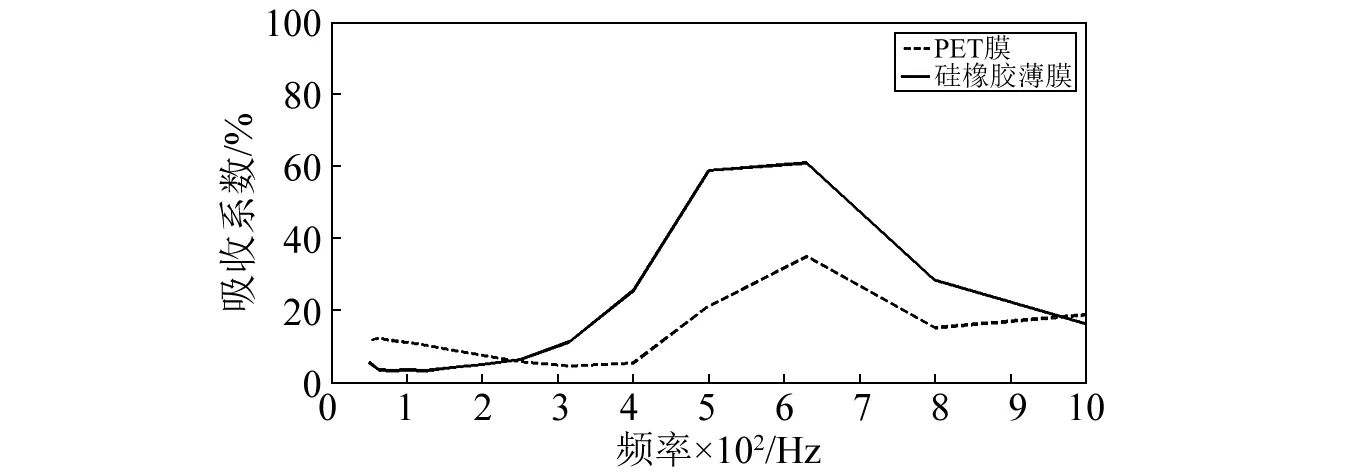
图12 声学特性曲线Fig.12 the sound absorption property curve

图12中可以发现，在250～1 000 Hz范围内硅橡胶薄膜对声波的吸收效果较PET薄膜强，在450～850 Hz低频范围内的平均吸收系数在0.5以上，该薄膜对低频声波具有很好地吸收性能，这种吸收来源于薄膜自身弯曲振动与入射声波存在较好的吻合形式，即与声波存在一定的弱耦合，但总体来说并没有达到理想的低频吸收要求，为此，需要一种质量-弹簧局域共振机制对声波进行很好地吻合吸收。为了进一步探讨薄膜刚度对声波吸收的影响，分别将四周固支的PET薄膜和硅橡胶薄膜的一侧镶嵌9个总质量为12.9 g的金属片，依次进行吸收测试，如图13所示。

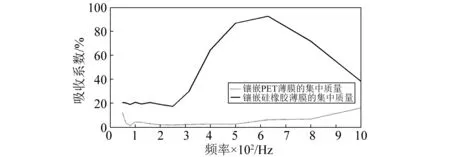
图13 镶嵌不同薄膜结构的吸收特性分析Fig.13 Inlaid with different stiffness membrane absorption sound property

通过对图13两组吸收特性曲线进行比较，可以看出镶嵌硅橡胶薄膜集中质量比之前硅橡胶薄膜的吸收效果有很大提高，且具有较高的吸收峰值，平均吸收系数在0.6左右。而镶嵌在PET薄膜上的集中质量形式比PET薄膜本身吸收系数更低，基本上没有吸收，几乎都以反射形式存在，本节所研究的镶嵌PET薄膜吸收结构并没有激发质量-弹簧共振系统，即PET薄膜与金属片之间没有相互作用，通过PET薄膜结构的行波在两部分之间的刚性作用几乎无损耗的反射回来，两者不存在对声波吸收的共振机制。

镶嵌在不同刚性薄膜表面上相同谐振单元的两种声学材料对低频声波的吸收存在本质上区别，通过试验对比发现，硅橡胶薄膜与金属片形成的弹簧质量系统与入射声波能够很好地吻合。为了方便理解，我们可以看成附加的集中质量对薄膜的弯曲振动进行了有效约束，其振动形式对声波起到很好地吸收效果。再从波形转化角度考虑，作为纵波形式下的入射声波通过声学超材料进行了剪切力及弯矩形式的转化变为横波，其声波能量得到削弱，产生很少的反射声波，也体现了声学超材料的吸收性能。

4.2 结构胞元与周期结构的吸收特性分析

为了分析谐振单元质量对结构胞元吸收峰位置的影响，同时，考虑单个质量-弹簧系统的振动特性，需要设计单个金属片与单元薄膜组成谐振单元的吸收结构。因此，选取一种刚度特性远大于硅橡胶薄膜刚度的PVC板，作为入射声波的反射面。

为了说明PVC板对低频声波的反射效果，将试件放到驻波管内进行声学测试，得到在0～1 000 Hz范围内吸收特性曲线，如图14所示。

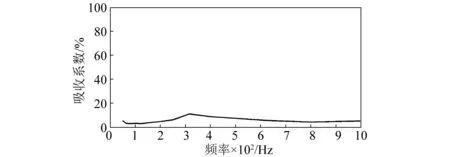
图14 PVC板的吸收系数频谱图Fig.14 The PVC board absorption coefficient frequency graph

从图14可以看出，该平板的平均吸收系数在6%左右，此时，经过该平板的声波几乎都以反射的形式存在，入射声波能量近似等于反射声波能量。因此，PVC板可以作为反射声波的刚性介质。

在2块PVC板中央截取为20 mm×15 mm的方形孔，采用黏结剂将硅橡胶薄膜黏附在两个PVC板中间，将集中质量黏结在方形孔中硅橡胶薄膜表面上。此时，整体结构看作集中质量与单元薄膜之间的振动形式。由于PVC的边框硬度足以在阻抗管中进行吸收测试，因此，得到一种谐振单元吸收结构，其平面结构如图15所示，局部放大结构如图16所示。

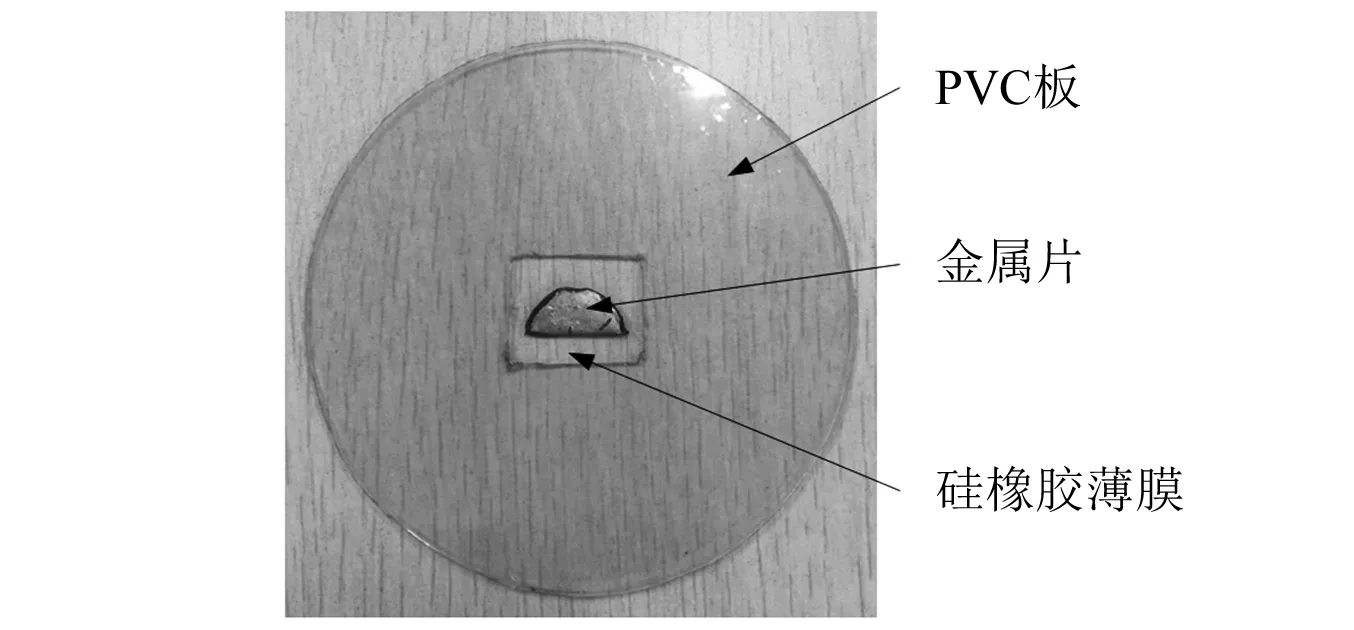
图15 谐振单元平面结构Fig.15 Resonance unit plat structure

图16 局域放大图Fig.16 Local strength graph

虽然，本文设计的薄膜型声学超材料满足结构胞元的周期分布，但是，每个结构胞元的振动形式与彼此之间的相互耦合作用影响是一个未知数，因此，结构胞元和周期结构胞元的吸收特性存在很大差异。为了进一步分析结构胞元与具有周期结构胞元声学超材料的吸收特性关系，选取9个谐振单元质量为(14.6/9)g的声学超材料(每个结构胞元中心距离为20 mm)，进行试验测试，得到吸收特性曲线，如图17所示。同时，将谐振单元是(14.6/9)g的结构胞元平面结构进行吸收测试，如图18所示。

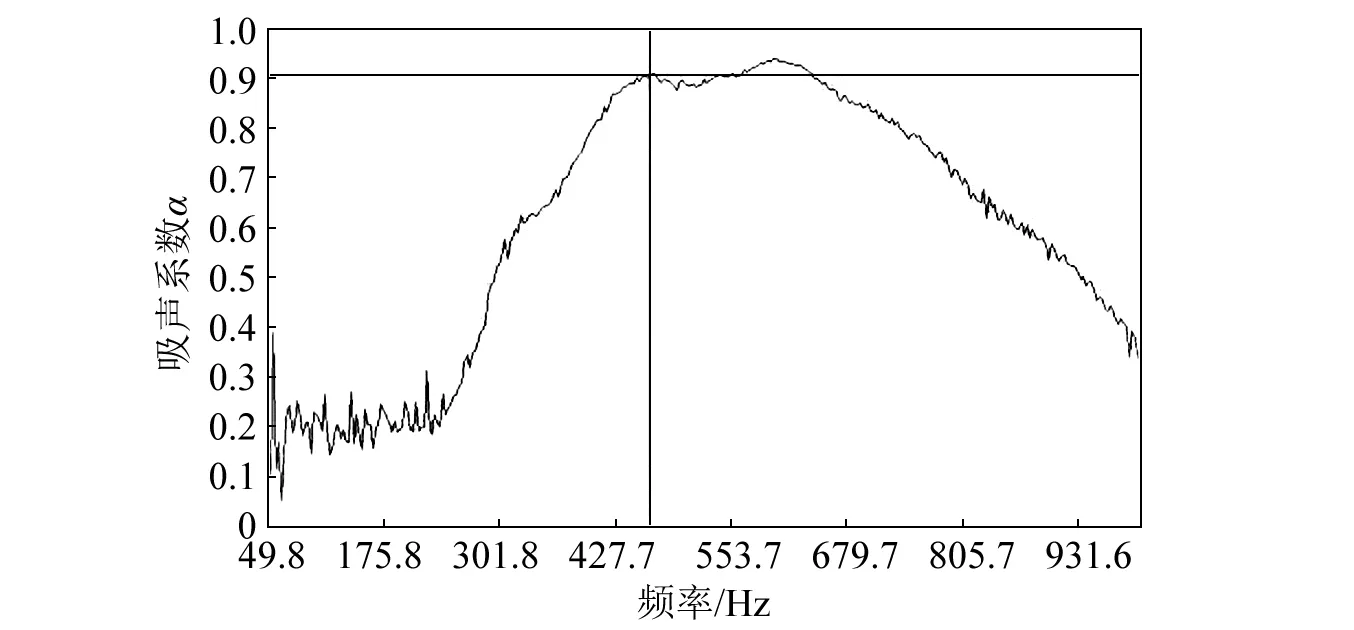
图17 声学超材料吸收系数频谱图Fig.17 Acoustic metamaterial absorption coefficient graph

分析图17、18可知，对于9个谐振单元质量为(14.6/9)g的声学超材料，其第一个吸收峰位置为468.8 Hz，而仅有单个谐振单元的吸收结构吸收峰位置是445.3 Hz，二者相差23.5 Hz。对于结构胞元和由多个结构胞元组合成的复合材料吸收特性来说，复合结构的吸收带隙较宽，吸收系数达到0.6以上的频率范围在377.9～848.8 Hz，并且在588.9 Hz达到了第二个吸收峰值，整体的吸收效果明显。而结构胞元的吸收带隙很窄，只有在392.6～544.9 Hz的一小段频率范围吸收系数达到0.6以上，且吸收峰值仅有一个，吸收效果不佳。结构胞元的吸收带隙很窄，其引发的局域共振特性较差，因此，需要多个结构胞元的耦合效果，增强结构的共振特性，使吸收效果达到最佳。

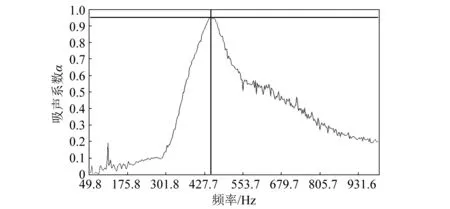
图18 结构胞元的吸收系数频谱图Fig.18 Unit structure absorption coefficient graph

在吸收效果方面，单个谐振单元的吸收结构与多个谐振单元组成的周期结构存在明显差异，周期结构的吸收性能并不是每个谐振单元吸收特性的叠加，而是多个谐振单元之间相互耦合作用的结果。具体表现为周期结构和结构胞元在第一个吸收峰位置差异很小，同时，周期结构胞元之间的耦合作用导致了吸收带隙拓宽，使总体的吸收效果显著。

5 结 论

本文提出的薄膜超材料是在振动吸收器基础上，引入质量-弹簧系统理论，通过明确负质量材料的属性，分析了金属片与薄膜之间的耦合作用对声波吸收形式的影响。再利用有限元分析了子结构胞元和镶嵌薄膜结构的振动形态，数值模拟了金属片对薄膜法向位移的约束作用，同时说明了理论模型的合理性。通过谐振单元的理论形式与结构胞元的振动形态进行比较，得到二者吸收机理相同的结论。接着，对两种不同薄膜材料属性进行定义，并进行仿真分析和试验研究，得到两种不同刚度薄膜的声学材料对声波吸收影响很大的结论。最后，通过试验分析了结构胞元与周期结构声学特性的差异，得出二者的吸收峰位置吻合较好结论，但是周期结构中胞元之间的耦合作用导致了低频声波带隙拓宽，吸收效果显著提高。