高频数据瞬时波动率核估计的窗宽选择及算法研究

王江涛，周 勇

(1.上海财经大学统计与管理学院，上海 200433；2.华中师范大学经济与工商管理学院，湖北 武汉 430079；3.中国科学院数学与系统科学研究院，北京 100190)

1 引言

波动率的准确度量问题一直是金融计量研究中的持续热点问题。对于波动率的度量，最初的做法是通过构建参数模型，利用低频数据进行估计。Engle和Rusell[1]提出的ARCH模型、Bollerslev[2]提出的GARCH模型及其衍生的一系列模型是这方面工作的代表。但是这类方法在度量波动率的准确性方面总是不尽如人意。为了更加准确地度量波动率，在结合高频数据的基础上，研究者提出了波动率的许多非参数估计量，如Vetter[3]、Zhang Lan等[4]、Jacod等[5]和Bandorff-Neilsen等[6]。随着金融市场的发展，各种交易活动越来越频繁，使得波动率度量的及时性显得尤为突出。这就需要准确地度量交易中每个时刻对应的波动率—瞬时波动率(Spot Volatility)。这方面的工作正在被丰富中。Fan Jianqing[7]在不考虑市场噪音下提出了瞬时波动率的核估计。Kristen[8]构建了一种瞬时波动率更加一般形式的核估计量。Zu Yang[9]在考虑市场噪音效果下，提出了瞬时波动率的一种新估计量。Sabel等[10]采用小波变换的方法构建了瞬时波动率的另外一种估计量。研究瞬时波动率的最新进展可见Mancini1等[11]、沈根祥[12]和吴鑫育等[13]的工作。

所有这些估计量都是瞬时波动率的非参数估计量，其实际度量瞬时波动率的效果取决于窗宽的选择。换句话说，这类估计量在实际应用中都面临着最优窗宽的选择问题。上述所有提出瞬时波动率非参数估计量的文章，虽然对如何确定其中的最优窗宽做了一些分析与讨论，如给出了最优窗宽的理论表达式、分析和讨论了最优窗宽理论表达式中未知参数的估计。但是这些研究还存在一些不足：首先，在已有的研究中，估计最优窗宽中未知参数的方法缺乏实用性，其根本无法从实际数据中估计出未知参数。如，Kristensen[8]在估计瞬时波动率轨迹的光滑参数时，假设已知瞬时波动率各个时刻的值。然而瞬时波动率在各个时刻的数值恰恰是待估计的未知量，不可能事先已知。Zu Yang[9]中对最优窗宽中的另外一未知参数—瞬时波动率高阶矩的积分进行估计时，所采用的方法中存在另外一个窗宽选择问题。其次，已有的研究并没有在具体应用中，讨论估计量的窗宽选择，而仅仅是在用数值模拟方法分析估计量的度量效果时，才计算了最优窗宽的具体值。这种情况下，由于事先能从数值模拟环节中清楚地知道瞬时波动率各个时刻的值，从而使得计算最优窗宽中的未知参数变得相当容易。因而最优窗宽也可以轻易得到。然而，在瞬时波动率非参数估计量的实际使用过程中，瞬时波动率的各个时刻值并不是已知的，这种情况下如何去确定估计量的最优窗宽，现有的研究并没有给出明确的回答。如，Figueroa-Lopez等[14]虽然也讨论窗宽的选择，给出了最优窗宽的表达式，但并没有给出从实际数据中计算窗宽的具体办法。

针对瞬时波动率非参数估计量中窗宽选择的研究现状，本文以瞬时波动率的核估计量为例，设计出一种能直接从交易数据中计算出最优窗宽具体数值的算法。事实上，确定瞬时波动率非参数估计量中最优窗宽的困难在于，其中的未知参数难以估计。因为这些未知参数往往依赖于待估计的瞬时波动率。基于对这种事实的观察，本文采用迭代的方法，通过设计算法，用逐步逼近的手段，来获得最优窗宽的具体值。算法设计的具体步骤是：首先，由某一个较为粗糙的窗宽开始，计算出瞬时波动率的第一次估计值，并由此得出最优窗宽中各个未知参数的估计，从而进一步计算出另外一个近似最优窗宽。然后，用该窗宽替换原来所使用的窗宽并重复该过程。只要迭代算法设计得合理，就能使得每一次迭代得出的窗宽都比原来所使用的窗宽更靠近最优窗宽。在构建算法之后，本文从理论上证明所构建的算法是稳定的和收敛的。算法经过有限次迭代之后能确定一个窗宽值，这个值不依赖于初始窗宽的选择，而且是最优窗宽的一致估计量。然后，我们将所构建的算法应用于实际数据当中，数值验证的结果表明文中的算法在有限容量的样本中表现也相当好，从而确保了算法的实用性。最后，将算法应用于模拟数据中，检验了由算法确定的窗宽的实际效果。结果显示，算法确定的窗宽是有效的，其确实是实际数据对应的最优窗宽。同时，如果将文中的算法进行改进和推广，就能解决瞬时波动率其他非参数估计量中最优窗宽的选择问题。

2 瞬时波动率的核估计

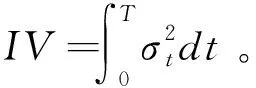
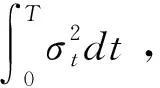
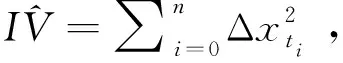
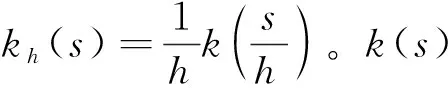
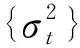
(1)

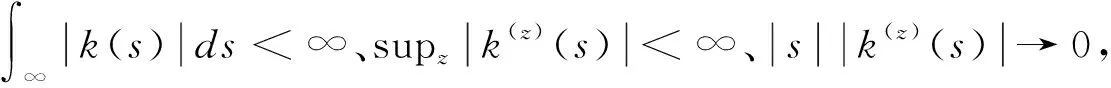
除了上述瞬时波动率核估计的这些理论性质，该估计量在实际应用过程中还存在两个问题。首先是非参数核估计量都面临的边界效应问题。在临近边界的附近估计瞬时波动率时使用边界核函数就可解决这个问题。第二个问题是，核函数的选择。不同的核函数影响瞬时波动率核估计量度量的效果并不大。本文中我们采用Parzen核函数。

3 最优窗宽及其参数估计

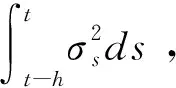
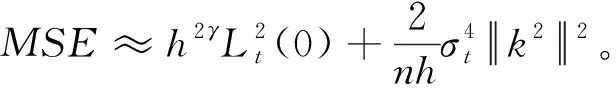
使得MSE在整个交易时间[0,T]内积分最小，就得到一个整体最优窗宽hopt：

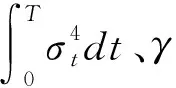
3.1 未知参数的估计

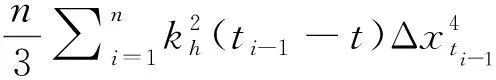
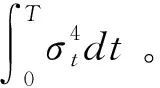
3.2 平滑系数γ的估计

平滑系数γ在确定瞬时波动率非参数估计量的最优抽样频率、最优窗宽和度量估计量的收敛速度等方面有着重要的作用。Blanke[17]研究了满足Hold条件的瞬时波动率过程平滑系数的估计。依据作者的研究结果，平滑系数的一种估计量为：

其中l，k均为正整数。在实际应用过程中，l和k的取值为1或2较为合适。Δ是连续交易之间的时间间隔。该估计量具有较好地理论形式，具体见Blanke[17]。Kristensen[8]在对瞬时波动率核估计中最优窗宽的讨论中建议用该方法对平滑系数γ进行估计。为了提高对估计的精度与准确性，作者还提出了γ另外一种形式的估计量：

(2)

其中l1，l2和k是取值为1或2的整数。

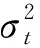
3.3 未知参数的估计

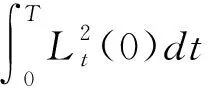
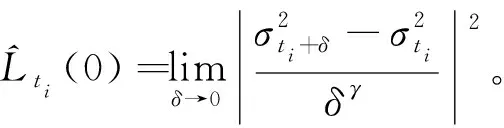
4 确定最优窗宽的算法

上一节中虽然分析了最优窗宽中未知参数的估计，但其中提出的方法在实际应用中都有一个前提条件：需要事先知道瞬时波动率在各个时刻的数值，然而各个时刻的瞬时波动率是待估计的未知量，不可能事先已知。为此，我们借鉴非参数核估计中Gasser等[18]提出的代入迭代算法的思想来解决这一问题。其基本思想是：从某一个近似最优窗宽的初始窗宽开始计算，得出瞬时波动率的一个近似估计。然后用该数值计算出一个新的最优窗宽的近似值，最后用新得到的最优窗宽近似值替换上一次迭代计算中使用的初始窗宽，重复上一次计算过程。于是每一次迭代后，算法都能得到瞬时波动率和最优窗宽的一个近似估计值。只要迭代过程中算法设计得合理，就能使每一次得到的估计值比上一次的更加接近于瞬时波动率和最优窗宽的准确值。

将上述做法具体化，我们构建了如下的算法：

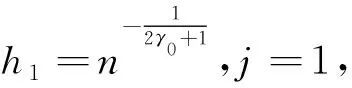
第二步：根据上一步得到的h1，令j=j+1，分别做如下计算：

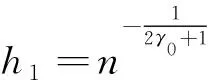
4.1 算法的收敛性

上述所构建的算法从任何初始值开始，经有限次迭代，最终都稳定地收敛到最优窗宽。

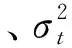
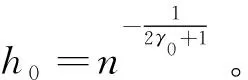
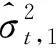
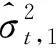
4.2 算法的实际数据表现

为了检验算法在有限样本中的表现，这一节将用两只不同的股票在某一个交易日内的价格数据和不同的初始值，即初始值γ0设定为不同的值，来考察算法在实际数据中的表现。本文选用了在德国证券交易所中交易比较活跃的法国航空公司2015年1月5日实时交易数据和上海证券交易所中交易比较活跃的中国神华(601088SH)2016年7月5日每隔5秒的分时价格数据。本文对原始数据做如下预处理：首先，删除在交易日时间外的所有数据，将中国神华上午和下午的数据当作连续交易数据对待；其次，删除数据中明显的由记录错误产生的数据，如交易价格或买卖的叫价为0的数据、买卖价差为负值或者大于临近交易的买卖差价10以上的数据等。同时还对交易时间做了伸缩变换，使得所有交易时间落在(0,1)范围内。这样操作并不影响最优窗宽的选择和瞬时波动率核估计的度量效果。

利用上述的数据，在不同的初始值条件下，在R软件中编程实现文中设计的算法，得到两只股票最优窗宽和迭代次数的关系图：

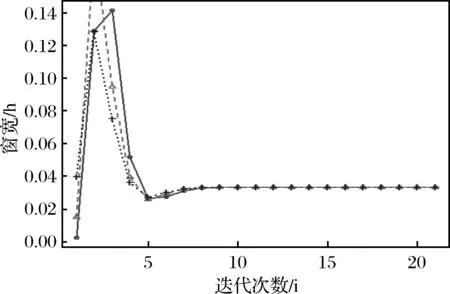
图1 迭代步数与所得窗宽图(法国航空公司)

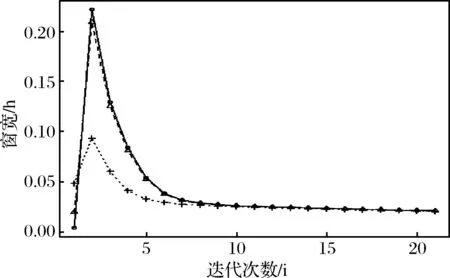
图2 迭代步数与所得窗宽图(中国神华)

上述两个图中，横轴代表迭代的次数，纵轴表示与迭代次数所对应的窗宽，图中的曲线描述了每次迭代计算所得的窗宽与迭代次数的关系。图1描述的是，算法应用于法国航空公司数据时，从不同的初始值开始，每次迭代后所得到的窗宽与迭代次数之间的关系图。图2是与中国神华交易价格数据对应的窗宽和迭代次数关系图。对于法国航空公司的价格数据，我们将初始γ0分别设定为0.2、0.5和0.8，其对应的初始窗宽h0分别为0.002483、0.01501和0.03956。从图1可以很容易地看出，刚开始的初始窗宽之间彼此相差很大。即便是经过两次迭代计算之后，窗宽之间的差距也比较大。从第四次迭代开始，不同初始值对应的窗宽之间的差距逐渐变小。经过12次左右的迭代，由不同初始值计算得到的窗宽之间基本上没什么大的区别，各个相差迥异的初始值在经过算法有限次迭代运算之后，都收敛到统一的窗宽。这表明文中提出的算法在实际数据的应用中仍然具有稳定性。为了进一步说明算法的稳定性，对于中国神华交易价格数据，我们分别设定初始γ0为0.2、0.5和0.8。其对应的初始窗宽分别为0.003536、0.01923和0.04786。从图2中仍然可以看出，前面三次迭代计算得到的窗宽之间相差比较大，随后每次迭代得到的窗宽之间的差异越来越少。经过12次左右的迭代之后，所得的窗宽最终收敛到一个统一的值上，这说明算法是稳定收敛的，而且收敛速度跟检验数据的选取和初始值的设定无关，完全取决于算法本身。上述这些数据验证的结果说明，文中的算法具有较好的稳定性和较快的收敛速度。

根据最优窗宽的理论表达式以及算法的计算步骤可以看出，算法只有在已知[0,T]时期内的交易数据(即，样本数据)之后才能计算出与之相对应的最优窗宽数值。而且其计算结果完全取决于样本数据。如果样本数据发生变化，或者样本时间由[0,T]延长到[0,T+t]，那么由算法确定的最优窗宽也将发生变化。以文中选取的法国航空公司交易价格数据为例，将开盘到下午5:00的交易作为分析对象，算法计算出这段时间内的最优窗宽为0.03416。但是以开盘到下午5:30的交易作为分析对象，算法确定出整个交易日内的最优窗宽为0.0333。由此看出，样本时间延长半个小时将使得最优窗宽降低约2.5%。

对于所选择的数据来说，由算法确定的整个交易日内的最优窗宽分别为0.0333和0.02059，与此相对应的瞬时波动率，其部分表现如下图所示：

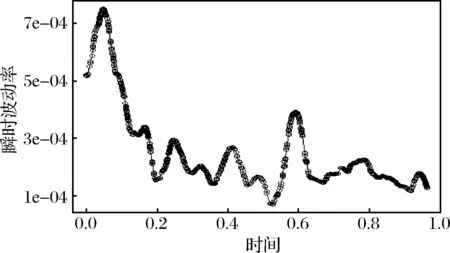
图3 瞬时波动率的部分表现图(法国航空公司)

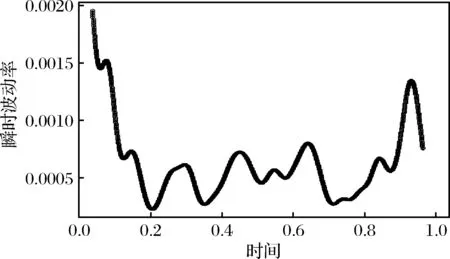
图4 瞬时波动率的部分表现图(中国神华)

从图3和图4中可以看出，在整个交易过程中瞬时波动率并非固定不变，而是具有时变性。而且其随时间的变动情况也呈现出一定的“日内效应”即，瞬时波动率在上午交易刚开始的一段时间内，数值都比较大。随着交易过程的稳定，其数值又逐渐回落到低位。但是在下午的交易过程中，瞬时波动率又会呈现出一次上扬，只是两只股票各自上扬的时间点不相同。瞬时波动率的这种日内变化模式与股票交易的实际过程完全吻合。除此之外，两只股票的瞬时波动率，其随时间的变化规律还具有各自不同的特点，这可能是由不同的市场规则和各自不同的交易过程而造成的。

4.3 算法的模拟数据检验

如果我们不是依据算法严格从实际数据中求出最优窗宽，而是人为地设定窗宽数值并以此计算瞬时波动率，将会造成最终的估计结果严重失真，甚至得到错误的结论。下面我们用模拟数据来说明这一点。本文考察了如下随机波动模型：

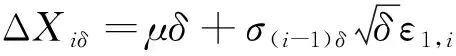
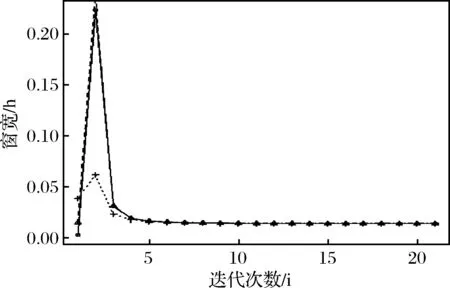
图5 迭代步数与所得窗宽图(模拟数据)

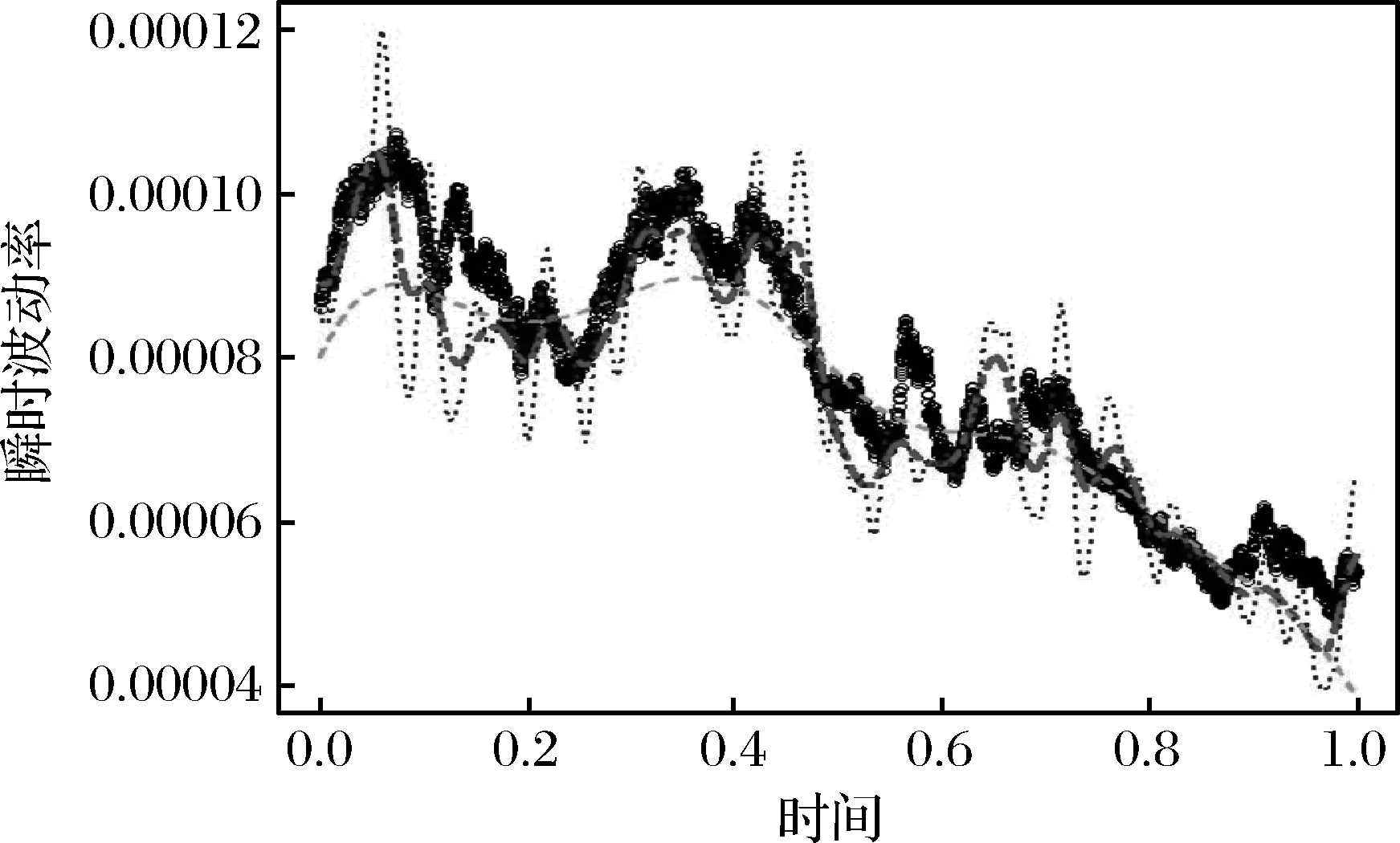
图6 不同窗宽下瞬时波动率的估计(模拟数据)

图5描述了将算法应用于模拟价格数据时，从不同的初始值开始，每次迭代所得到的窗宽与迭代次数之间的关系。图形显示算法在模拟数据中也具有稳定性，其确定的窗宽为0.01339。在该窗宽下，模拟价格数据的瞬时波动率核估计如图6中(红色)点虚线所示。从图6中可以看出，该窗宽对应的估计值能准确地描述真实瞬时波动率的变化轨迹。而且该估计量还具有较高的精度，在整个交易时间内其与真实瞬时波动率的相对绝对误差平均值仅仅为6%。这些结果表明由算法确定的窗宽确实是模拟价格数据对应的最优窗宽。此时，瞬时波动率估计量的绝对误差平均值(简记为：MAE)为4.6618×10-6。如果估计中采用人工设定的窗宽，如0.065和0.0065(其分别是最优窗宽的5倍和1/2倍)，此时得到的瞬时波动率估计值分别如图6中(绿色)线段虚线和(蓝色)圆点虚线所示。从图中可以看出，这两个窗宽对应的估计量都无法准确地描述真实瞬时波动率的变化。两估计量中都具有较大的偏差，其对应的MAE分别为5.3319×10-6和7.0378×10-6。它们分别是最优窗宽对应的绝对误差均值的1.1437倍和1.5097倍。因此平均而言，在最优窗宽下瞬时波动率估计量的误差比在人工设定的窗宽0.065和0.0065下估计量的误差要低，其降低的幅度分别为14.4%和50%。由此可以看出，只有在最优窗宽下计算瞬时波动率估计值，才能够保证最终的结果有意义。因此本文提出的算法具有重要的作用。

上述算法虽然仅仅是针对瞬时波动率核估计量而设计的。如果按照算法设计的思路，将文中的算法做恰当的调整，就可用来确定瞬时波动率其他非参数估计量的最优窗宽。从而彻底解决从实际数据中估计瞬时波动率存在的困难，为瞬时波动率的各种实际使用如，风险管理和期权定价等提供数据支持。在风险管理方面，可以先用瞬时波动率对每次收益率进行标准化处理，在此基础上计算VaR的值。根据相关的理论结果，这种做法可提高风险度量的准确性。在期权定价方面，将计算出来的瞬时波动率直接代入到各种期权定价公式，如B-S公式中，就可进行期权定价。

5 结语

最优窗宽的确定是瞬时波动率非参数估计量在实际应用过程面临的一个重要问题。由于最优窗宽中往往含有难以估计的参数，使得该问题并不容易解决。本文以瞬时波动率核估计为例，提出了一类能从价格数据中获得最优窗宽的算法。然后，从理论上证明了该算法是收敛的而且具有稳定性。将所构建的算法用于实际数据当中，结果显示该算法所确定出的最优窗宽不依赖于初始值的选取。无论将初始值设定为其理论范围内的哪一个值，由算法所确定出的窗宽最终都收敛到统一的最优窗宽上。将文章中的算法进行推广与改进，就可以用来确定瞬时波动率其他非参数估计量的最优窗宽。从而为瞬时波动率的后续研究和实际使用如，风险管理、期权定价和市场微观结构的探究等铺平道路。