重尾指数估计量及其伪估计量的渐近关系①

刘洋， 彭作祥

西南大学 数学与统计学院， 重庆 400715

其中{Xi，n， 1≤i≤n}为其升序统计量． 有关极值指数估计量及其应用的更多研究见文献[6-14]．

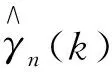
(1)

对所有x>0成立． 显然，A(t)∈RVρ，ρ≤0．

对连续可微单增函数f(x)， 定义

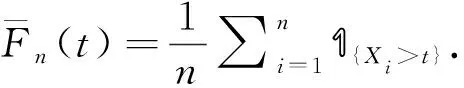
(2)

特别地， 令f(x)= logx， 可以得到如下推论．

(3)

证使用分部积分法， 可得

再根据文献[2]的命题B.1.10， 当t充分大时， 对任意的δ>0有

(4)

同理，

引理1得证．

(5)

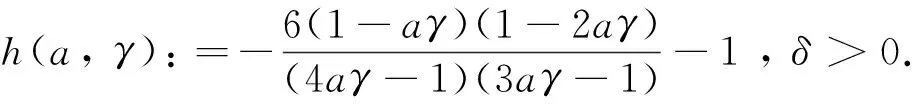
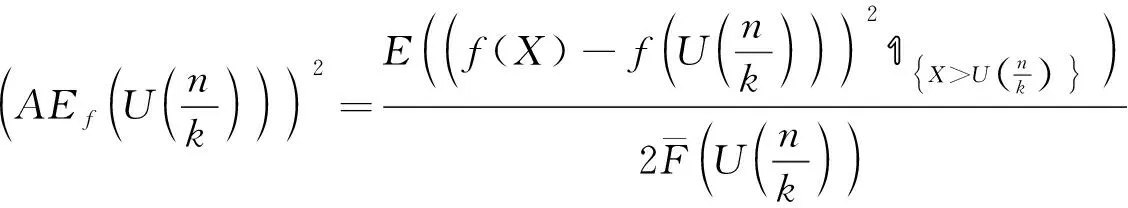
使用分部积分法， 可得

再结合引理1， 可得

此外， 当n充分大时， 对任意的δ>0有

定理1的证明使用分部积分法， 可得

(6)

(7)

将(6)式与(7)式分别平方后再相减， 可得

(8)

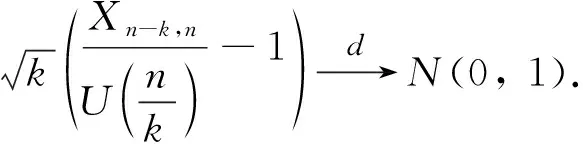
再结合引理1和文献[7]的引理1， 当n充分大时， 可得

接下来考虑等式(8)右边的第二项． 注意到

再根据引理2， 当n充分大时， 可得

从而有

综上所述， 当n充分大时， 可得

定理1得证．

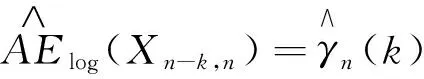
推论1得证．