基于Hawkes因子模型的股价共同跳跃研究

刘志东,郑雪飞

(中央财经大学管理科学与工程学院，北京 100081)

1 引言

Merton[1]较早地提出了扩散-跳跃模型，他在经典B-S期权公式的理论框架下加入了跳跃项，认为跳跃是一些特殊信息引起价格的不连续变动。Barndorff-Nie1sen等[2-3]利用已实现变差(Realized Variance，简称为RV)和双幂次变差(Bipower Variance，简称为BV)的渐进分布来检验跳跃，Andersen，Bollerslev和Dobrev[4]、Lee和Myland[5]提出了局部波动率的概念，提出了能够识别准确时间的跳跃检验方法。在ABD、LM跳跃检验的基础上，如果同时对多只股票进行跳跃检验，则可以把相同时间发生的跳跃称之为共跳(Cojumps)。对共跳问题进行分析有助于对系统性风险、市场风险传导等问题进行深入研究。其他对于共跳的研究是从二维资产价格过程开始的，如Barndorff-Nie1sen和Shepharcl[6]、Gobbi和Mancini[7]、Jacod和Todorov[8]等。Bollerslev等[9]在二维资产价格研究的基础上提出了BLT共跳检验，他们在利用BN-S方法检验股票和由个股组成的等权重指数跳跃时发现，个股跳跃频率比指数跳跃频率要高，而且个股之间的跳跃和指数之间的跳跃没有明显的关系。作者进而提出了基于CP统计量(Cross Product)的共跳检验方法，这种方法的逻辑是，如果一个可分散风险组合发生了跳跃，这个跳跃只能是由于资产同时跳跃产生的，即共跳。Liao Yin等[10]基于BLT提出了First-High-Low-Last方法。这种方法本质与BLT类似，但是用到了每个时间区间的开盘价、最高价、最低价以及收盘价。作者利用这四种价格的线性组合对共跳进行检验，并且证明利用这种方法得到的估计量相比于BLT方法中的估计量更为有效，均方根误差更小。

Bajgrowicz等[11]提出了基于错误发现率(FDR)的阈值跳跃检验，作者认为目前的非参数检验方法由于多重检验问题而存在大量伪跳。随后，作者基于高频数据进行了跳跃检验，结果显示，之前的非参数检验结果90%左右均是伪跳，没有显著的证据说明跳跃存在聚集性，不能拒绝“泊松跳”的假设，并且没有观察到所有样本股票共跳的现象，说明跳跃风险是可以分散的。在描述跳跃特征方面，目前主流的理论和实证研究认为纯跳跃是复合泊松过程。泊松跳跃过程的优势是解析式可处理，然而，现实中不仅单个资产价格中的跳跃过程呈聚集性，而且，随着金融市场的联系越来越紧密，不同资产价格跳跃发生的时间也表现出某种同步性。这种同步性最明显的例子是2010年5月6日发生在美国市场的“闪电崩盘”。根据美国证券交易委员会和美国商品期货交易委员会的统计，“闪电崩盘”最初发生在EMiniS&P 500市场价格急速下跌，然而，在非常短的时间，这种价格下跌向ETFs、股票市场指数及其成份股、衍生品扩展和传播，道琼斯工业平均指数在数分钟之内下跌9%，这种传染效应在流动性市场极其迅速，导致很多资产价格出现明显的同步不连续跳跃。这些系统性事件不能被假设价格跳跃是独立过程的泊松模型描述。Gilder等[12]采用高频数据发现股票趋向于系统性共跳的证据，拒绝了股票跳跃发生时间独立的假设。

基于这些明显偏离独立泊松模型的经验和事实，有必要采用合适模型表示资产跳跃过程。Bormetti等[13]认为“泊松跳”不足以解释观察到的资产价格跳跃聚集性和大量共跳存在的事实，建议将Hawkes过程应用于跳跃和共跳研究。Hawkes过程最早由Hawkes[14]提出，之后主要应用于地震数据的研究。在Bormetti等[13]之前，已经有学者开始将Hawkes过程应用于数理金融和计量经济学领域的研究。例如，Bowsher[15]将Hawkes过程应用于金融时间序列分析中，Bacry等[16]将Hawkes过程应用到对一维和二维逐笔数据的方差建模中，借此来研究微观噪声(如均值回复)和Epps效应等。

Hawkes过程由于其跳跃强度是时变的，这一特性可以很好地解释跳跃的聚集性。但是，直接将单个Hawkes过程扩展到多维资产过程时却存在问题，其中之一是多维Hawkes过程需要估计的参数呈指数形式上升。Aït-Sahalia等[17]采用多维Hawkes模型描述跳跃扩散过程，来刻画在危机期间的金融传染，并给出在此条件下对数效用投资者最优消费和投资问题，采用广义矩估计方法对模型参数进行估计。但是该方法由于参数估计计算效率较低，使其应用中维数受到限制，多数情况下只能用来研究两种资产跳跃。而采用因子Hawkes模型可以解决此问题。

目前，国内学者对于共跳的研究较少。唐勇和林欣[18]采用常用的日内跳跃检验方法，构建了共同跳跃(协)方差和连续样本路径(协)方差，并扩展HAR-RV-CJ模型，将(协)方差、共同跳跃置于统一波动模型框架内。通过对上证综指和深圳成指高频数据的实证分析，结果显示两指数共同跳跃占其各自的跳跃比例较大，且基本上都是同方向的跳跃；共同跳跃(协)方差和连续样本路径(协)方差对已实现(协)方差的影响都是显著的，考虑共同跳跃影响有助于提高(协)方差建模的准确性。在跳跃、共跳和宏观信息方面，赵华和秦可佶[19]采用非参数跳跃识别方法，利用沪深300指数的高频数据，对中国股市跳跃性和宏观信息冲击的关系进行研究。

为此，本文拟引入Hawkes因子模型描述系统性的共跳，假定存在一个无法观测的点过程表示市场因子，当该因子发生跳跃时，每种资产以不同的概率发生跳跃。通常每种资产价格跳跃也包含异质性点过程。为了捕捉跳跃聚集性，本文采用Hawkes过程对点过程建模。并给出如何对模型进行估计，以及如何区分系统性跳跃和异质性跳跃。并通过实证和仿真研究展示该模型能够在纵向和横向截面上重现多资产跳跃过程。

2 共跳检验方法比较

共跳检验方法可以分成两大类，一种是基于单个资产跳跃检验的共跳检验，这包括：BN-S检验方法、ABD和LM检验方法。由于这些方法在研究单个资产跳跃中应用较多，本文在这里不再详细赘述，具体可参见相关文献。本问在这里重点介绍基于多资产的共跳检验方法。

考虑一维资产的价格过程，通常认为，资产的对数价格pt满足以下过程：

dpt=μtdt+σtdWt+κtdQt

(1)

其中，μt表示漂移系数，在研究高频数据时，一般假设漂移系数为0。σt表示扩散系数，Wt是一个标准布朗运动，κtdQt在这里表示一个纯跳列维过程，通常假设这个列维过程是一个复合泊松过程，本文用κt表示跳跃的幅度，其跳跃强度是常数，而跳跃的幅度是独立同分布的。

研究中，对于单个资产，每天可观察到的等时间间隔的对数价格有M+1个，时间间隔为δ，那么，第t天第j个收益可表示为:

(2)

这样得到了每个交易日M个收益的收益序列。

定义交易日t的已实现变差RVt(Realized Variance)为：

(3)

在有跳跃的情况下，当M→∞时，RVt将收敛于积分变差和跳跃平方之和：

(4)

其中，Nt表示第t个交易日跳跃的数量。

2.1 BLT方法

BLT方法是在BN-S检验方法的基础上建立起来的。首先，Bollerslev等[9]构建了n只股票的等权重组合(Equiweighted Portfolio)：

(5)

将BN-S中的RV、BV概念移植到等权重组合中：

(6)

相应的还有：

BVEQW,t=

(7)

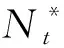
(8)

这里为了方便表示，本文应用了不同的符号，当n足够大时，上式中的第一项可以忽略，第二项的系数近似等于1，因此：

(9)

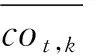
为了检验共跳，Bollerslev等[9]提出了CP(Cross Product)统计量：

(10)

CP统计量描述了多只个股之间两两协同运动情况，将t交易日的CP统计量相加，得到：

(11)

当n足够大时，第二项可以忽略不计，这说明cpt对单个股票的特异性运动是不敏感的，而对组合的同时性运动即共跳是敏感的，当组合出现跳跃时，有理由相信cpt的值将变大。

从理论上很难证明CP统计量的分布情况，本文采取靴攀法(Bootstrap)，首先将CP统计量标准化：

(12)

其中，

(13)

(14)

然后利用蒙特卡罗模拟确定该统计量在要求的显著性水平下的阈值。

2.2 FHLL方法

BLT方法只利用了每个交易区间的开盘价和收盘价，Liao Yin和Anderson[10]在BLT方法的基础上提出了FHLL方法。FHLL方法利用了每个交易区间的开盘价ptj-1、收盘价ptj、最高价htj-1和最低价ltj-1。在前面的BN-S跳跃检验方法中，RVt可以表示为：

(15)

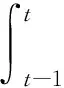
(16)

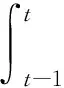
基于以上理论，FHLL方法构建了更加有效的估计量：

(17)

本文将FHLL方法中的统计量记为FHLLC，和CP统计量类似，可以构造相应的检验统计量：

(18)

其中，FHLLVEQW,t是等权重组合的FHLLV值，在构建组合时，首先分别计算每个时刻所有样本股开盘价、收盘价、最高价、最低价的平均值，然后以平均值计算出组合在每个时刻的FHLLV值，再将每个交易日的FHLLV值累积求和，得到组合一个交易日的FHLLVEQW,t的值。

同样，将FHLLC统计量标准化，得到：

(19)

其中，

(20)

和BLT方法类似，FHLL方法统计量的阈值也需要通过蒙特卡罗模拟进行计算。

3 共跳检验的实证分析

3.1 数据描述

本文从沪深300成分股中选取了50只股票，这些股票在2013年1月21日至2016年1月21日三年的时间跨度中均没有停牌，交易记录是连续完整的，本文所有交易高频数据均来自WIND金融咨询。本文通过两个指标来确定较为合适的数据频率，一是Andersen等[20]提出的波动率特征图，即通过计算不同数据频率下日平均RV，选择使得RV较为平稳的数据频率，如果RV相对平稳，则说明微观噪声的影响已经弱化。二是零收益占比，如果数据中出现较多的零收益，会对跳跃检验产生影响。本文计算了部分样本股的日平均RV和零收益占比，结果显示，数据频率大于5分钟之后，其日平均RV较为平稳。各股零收益占比随着数据频率的降低显著下降，数据频率大于5分钟之后，零收益占比较为稳定，大部分在5%以下，值得注意的是，样本股中市值最大的个股工商银行(601398)交易较为活跃，零收益占比较高，但5分钟频率数据比1分钟频率数据的零收益占比下降了近50%。结合Aït sahalia等[21]的研究，为兼顾数据信息量和微观噪声影响，本文选择5分钟数据频率。

本文从WIND获取了50只股票除权除息之后的5分钟高频数据。由于每日开盘数据受到隔夜信息的影响，本文剔除了开盘价，价格序列从每个交易日的9点35分开始，到15点整结束，每只股票每个交易日有48个观察数据。2016年开始试行熔断机制，导致市场在新年第一个交易日就经历了熔断，随后马上再次出发熔断。为了避免熔断对数据的影响，本文剔除了两次熔断发生当日的交易数据，即2016年1月4日、2016年1月7日，处理后，每只股票共计728个交易日、34944个交易价格。

这50只样本股覆盖了25个不同行业，本文计算了样本股2015年最后一个交易日的市值，最低为天津港189亿元，最高为工商银行15751亿元，从行业和市值的分布情况看，样本股对于市场具有非常大的代表性。

由于高频数据存在波动率的日间U效应，即在开盘和收盘阶段，股票价格的波动率要大于其他时间，因此需要对数据进行处理，消除这种效应对跳跃和共跳检验的影响。根据Bormetti等的方法，本文将日间收益数据除以一个日间效应因子。

3.2 LM跳跃和共跳检验结果

50只样本股的LM跳跃检验结果显示，每只股票平均发生了103次跳跃，占数据总数的2.94%，最少的个股发生了51次跳跃，最多的个股天津港(600717)则发生了171次跳跃。巧合的是，跳跃发生最多的是市值最小的公司。本文统计了这些股票跳跃的方向、跳跃时间等信息，这里选取了10只股票的跳跃结果。

表1中选取的10只股票，跳跃次数从66次到171次不等，这里的跳跃概率由跳跃数量与总收益数据量相除得出，可以看到，这10只股票的跳跃概率最低为0.19%，最高为0.49%，以最高概率为例，大概200个收益序列中会出现一次跳跃，说明跳跃事件的发生频率是较低的。另外，平均跳跃收益统计了当跳跃发生时该股票在跳跃时间间隔的收益绝对值的平均值，本文挑选的10只股票中，平均跳跃收益最大的是机器人(300024)，达到了3.34%，这只股票来自创业板，这与市场直观印象是一致的：创业板的股票波动性更大，其他个股的平均跳跃收益基本在3%以下。

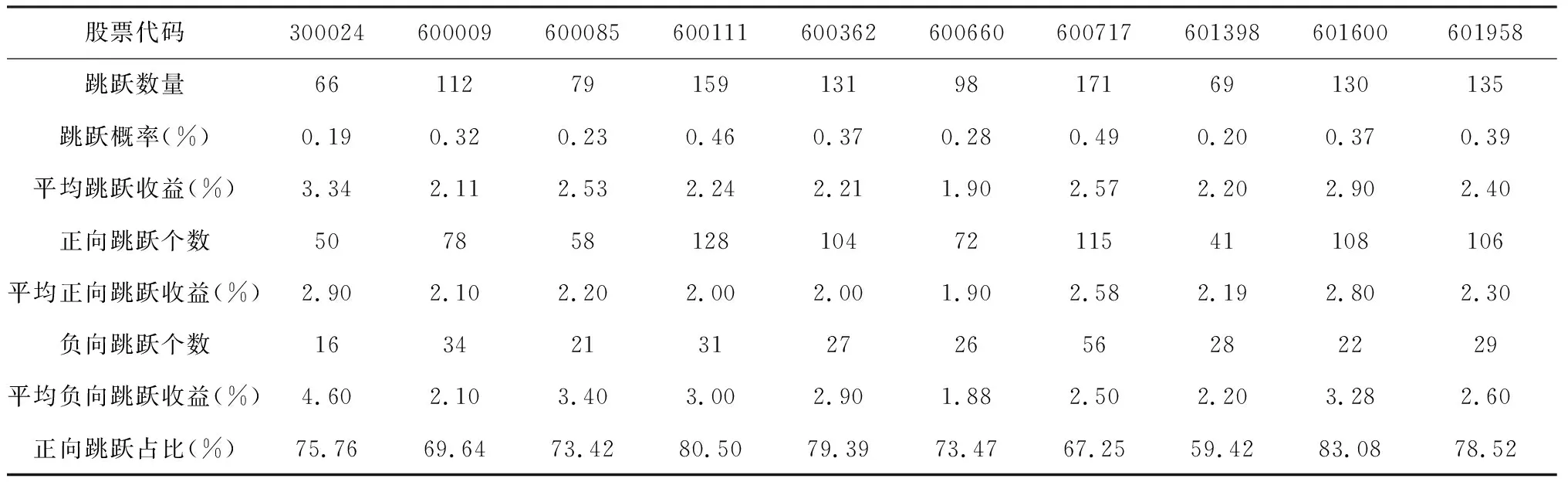
表1 部分样本股跳跃检验结果

本文研究了10只股票的跳跃方向，将跳跃发生时刻是正收益的跳跃称为正向跳跃，将跳跃发生时刻是负收益的跳跃称为负向跳跃，可以看到，10只样本股跳跃中大部分是正向跳跃，正向跳跃平均占比达到了74%，最低占比比例为59.4%，最高占比比例为83.08%，说明在上涨行情时，市场更容易追涨，使得价格在短时间内迅速拉升，触发跳跃。另一方面，由于我国股市存在涨跌幅限制，对于利好消息的反应不能一步到位，有可能是多个涨停才能彻底消化，这也进一步持续了上涨行情。但是本文注意到，虽然负向跳跃的数量占比很低，但是，本文选取的10只样本股中，只有两只股票的负向平均跳跃收益小于正向平均跳跃收益，有三只股票正负向平均跳跃收益基本相同，而有五只股票负向平均跳跃收益明显大于正向跳跃时的数值。本文认为，相比于上涨行情，引起快速下跌行情的情况较少，但是这些情况都比较严重，如有时个股会遭遇“黑天鹅”事件，这种事件的触发几率很小，但是触发后对价格的负面影响很大。

对于共跳，很多学者将两只或以上资产价格同时跳跃即作为共跳来处理，如Lahaye等[22]、Gilder等[12]，当发生共跳时，用公式表示如下：

(21)

其中，Ⅱ{Jumpt,i,j>0}称为共跳指示函数，当同时发生跳跃的资产大于2时，指示函数取1，不满足条件时，指示函数取0。Gilder也将这种判别标准称为“超越数”规则。

在个股LM跳跃检验的基础上，本文依照上述规则整理出了共跳的情况，本文将这种检验称为LM共跳检验。

表2统计了不同数量股票共跳的情况。一共观察到709次共跳，占数据总数的2%，这一比例要大于单只股票跳跃所占比例。同时有4只股票或以上跳跃的情况有146次，而至少20只股票一起跳跃的次数有9次，最多的情况发生在第一次熔断之后的首个交易时段，即2016年1月5日9点35分，一共有42只股票同时发生跳跃，占所有样本股票的84%；其次是第二次熔断之后的2016年1月8日9点35分，有30只股票同时发生跳跃。由于本文将熔断发生的两天交易数据剔除，可能导致前后交易数据连续性受到影响，因此本文单独将这两次大规模共跳定义为熔断共跳。

表2 LM共跳检验结果

针对20只股票以上的共跳情况，本文进行了详细分析，表3列出了这9种情况的具体时刻。9种情况中，除2016年两次熔断共跳外，2015年发生了5次，2013年发生了2次，2014年没有观察到这种情况。本文搜集了这9种情况发生时市场表现和重大事件，发现这9种情况都是在市场暴涨暴跌状态下发生的:两次熔断共跳、三次股市暴跌、两次深V反转、一次大涨、一次极端事件。从2014年7月开始，我国股市进入了上涨行情，沪深300指数从2014年7月1日的2164.56点一路上涨到2015年6月9日的5380.43点，涨幅高达148.6%，随后股市开始断崖式下跌，2015年8月26日，跌到2952.01点，随后市场开始小幅反弹，但进入2016年，又开始新的一波下跌潮。2015年经历了完整的市场动荡，因此大规模股票共跳次数最多。这说明市场在极端情况下，个股表现和市场关联度非常大，极易遭受市场情绪影响，这也解释了为什么大规模共跳发生时，个股跳跃方向基本是一致的，(除两次熔断共跳有跳跃方向不一致的情况发生外，其余情况共跳发生时，所有跳跃股票的跳跃方向是一致的)当市场趋势形成时，更容易出现追涨杀跌的情况，导致大多数股票价格随着市场行情方向运动。

表3 20只以上股票共跳情况

另一方面，2015年股市经历了多次暴涨暴跌，如上证综指跌幅超过5%的共有12次，检验结果只记录到这12次暴跌中的3次，说明并不是每次暴跌都会引起多只股票共跳，如果下跌行情是持续缓慢的，则价格路径也可能是连续的，并非能造成跳跃。相比于暴涨，暴跌可能更容易造成大规模共跳，因为2015年上证综指涨幅超过3%的情况有19次，但检验结果只记录了一次2.97%的涨幅情况。

本文对LM共跳的日间时间分布进行了分析，结果显示，开盘时间共跳数量最多，9点35分共跳占所有共跳的4.9%，达到了35次，而每个时间段的平均共跳个数是14次，开盘半小时内的共跳占全部共跳的14.5%。另外，由于我国股市有午间休息时间，下午13点开盘后，共跳数量也有所上升，下午开盘半小时内发生共跳占比达到了16.4%，高于上午开盘半小时内的共跳数，但各个时间段共跳数量分布相对平均，这说明市场对午间休息时积累的信息反应没有隔夜信息那么多，释放速度也较为缓慢，没有导致开盘即大量共跳的现象发生。其他时间段中，临近尾盘的14点30分共跳是最少的，随后共跳数量有所上升，但收盘阶段半小时的共跳只占所有共跳的10.5%，说明尾盘时间个股波动没有开盘时间剧烈。

3.3 BLT共跳检验情况

在讨论BLT共跳检验结果之前，首先要通过蒙特卡罗模拟确定BLT检验的阈值。

利用Euler分解模拟出50×1维的纯随机扩散过程(即没有跳跃项)，且漂移率为0，方差协方差矩阵为Σ=CC′,且模拟出的资产对数价格满足如下公式：

dps=C′dW(s)

(22)

这里，本文用ps表示50只股票的对数价格运动路径，W(s)是50×1维的相互独立的标准布朗运动。方差协方差矩阵Σ则采用了50只实证股票的对应数据。本文设置每天的时间为T=1，K表示每天模拟的收益数量，则每一个时间间隔表示为Δt=1/k，N表示一共模拟的天数。

首先生成Z1,Z2…Zk个相互独立的符合标准正态分布的R50随机向量，设置布朗运动的初始状态W(0)为50×1的零向量，则有：

(23)

对数资产价格的初始状态p0设置为50×1的零向量，则有：

pth+1=pth+C′W(th+1),h=0,…,K-1

(24)

这样就模拟出50只股票的对数价格路径，然后计算出相应的收益数据。

这里，每次模拟100个交易日的数据，再将这个过程重复100次，如果模拟5分钟数据，则每天生产48个交易价格，每天有47个收益数据，一共47万个检验统计量的原分布，然后计算出0.1%显著性水平下的临界值。从模拟情况下的检验统计量的分布情况，可以看出，BLT统计量呈现明显的右偏分布:

在模拟中，本文计算了不同时间频率、不同股票数量下CP统计量的临界值情况:

表4说明，CP统计量的临界值在不同显著性水平下差异较大，但同一显著性水平下，临界值对股票数量不敏感，三组不同数量的股票结果基本相同，但是临界值对数据频率非常敏感，在0.1%、1%水平下，随着数据频率的增多，临界值也明显增大，0.1%水平下，每日16个价格频率的临界值大概在3.5左右，但每日96个价格频率的临界值则在6左右。在5%水平下，临界值呈现不一样的特征：随着数据频率增多，临界值减少，但减小的幅度不明显。CP统计量呈现明显的右偏分布，在降低显著性要求时，临界值会迅速减少，但减少到一定程度后，由于大量数据都集中分布在左侧，临界值会趋于稳定。

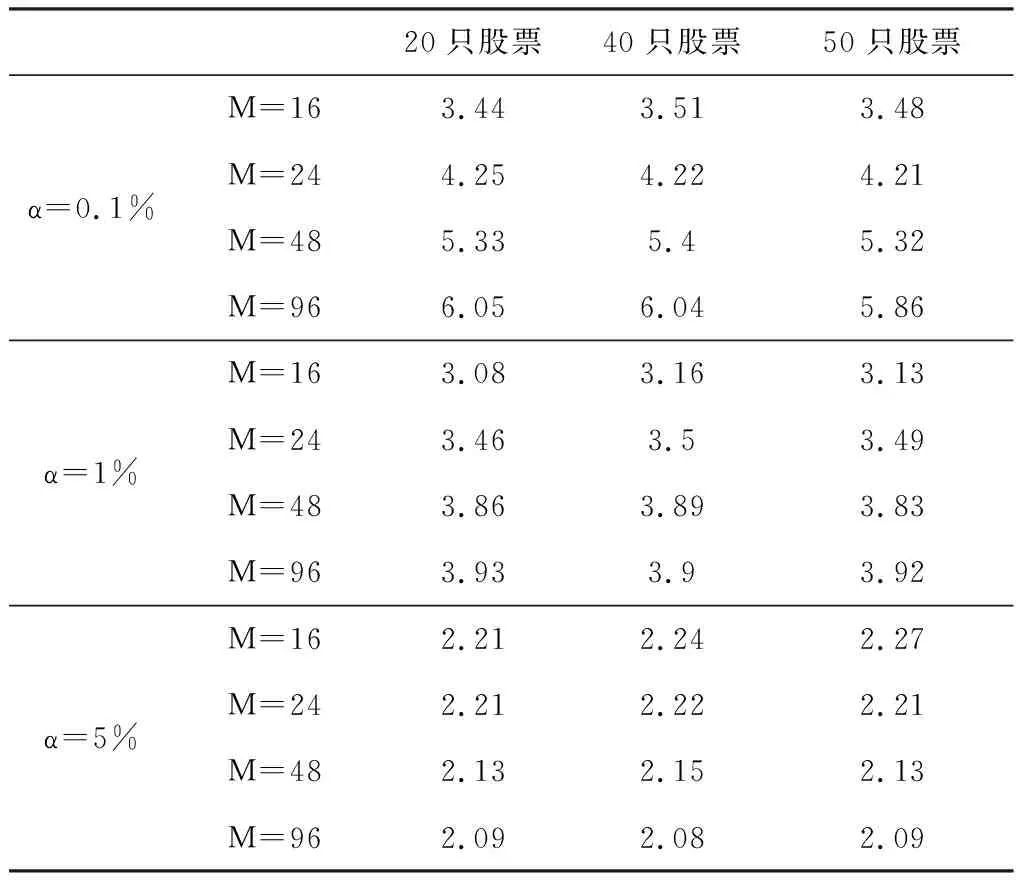
表4 CP统计量临界值

根据本文数据的实际情况，选取5.32作为0.1%显著性水平的临界值，得出了BLT检验结果。结果显示，50只股票一共出现了130次共跳，从共跳的年度分布看，2013年发生了43次，2014年发生了37次，2015年发生了48次，因为2016年数据量较少，只有两次共跳发生，但有一次共跳发生在2016年1月5日9点35分，即第一次熔断之后的首笔交易。

从共跳发生时的CP统计量的值看，有些时间段的共跳较为集中，但有些时间段共跳较少，共跳呈现一定的聚集性特点，本文将在后面的部分深入讨论这个问题。

本文针对BLT共跳的日间时间分布进行了统计，BLT共跳结果显示，开盘9点35分一共发生15次共跳，占比为11.53%，开盘半小时内的共跳占所有共跳的16.2%，其他时间段的共跳分布普遍在5次以下，下午14点之后，共跳数量有所增大，但临近尾盘阶段共跳数量明显减少。虽然方法不同，但和基于单个资产的LM共跳检验类似，大部分共跳发生在10点之前。

3.4 FHLL共跳检验情况

在描述BLT方法时，本文利用蒙特卡罗模拟得出了CP统计量的阈值。进行FHLL共跳检验时，依然遵循这一思路，由于FHLL需要得到每个时间段的开盘价(对数值，下同)、收盘价、最高价、最低价，在进行模拟时，本文设定每个时间间隔内有细分的10个观察值，在这10个观察值中，取首尾两项为开盘价和收盘价，除首尾外的最高价、最低价作为这个时间段的相应最高价和最低价，由此构建FHLL统计量，然后模拟得出了FHLL共跳检验的临界值为4.42，这一阈值比BLT的结果要小，这与Yin Liao和Anderson[10]的结论是一致的。FHLL检验结果显示，共有70次共跳发生，共跳次数是三种共跳检验方法中最少的，FHLL共跳的日间时间分布和之前的两种方法有所不同，由于共跳次数较少，有5个时间段的共跳次数时最多的，分别是9点35分、11点、13点20分、15点。虽然开盘9点35分的共跳次数也较多，但只占到所有共跳的5.7%，且没有明显比其他时间多，开盘半小时的共跳为10次，占比为14.28%。从FHLLV统计量的结构来看，由于用到了开盘收盘、最高最低等价格，此时的共跳条件要比单纯利用开盘收盘要严格，因此共跳的频率减少了。

3.5 共跳检验结果比较

本文对三种共跳检验方法进行了统计：

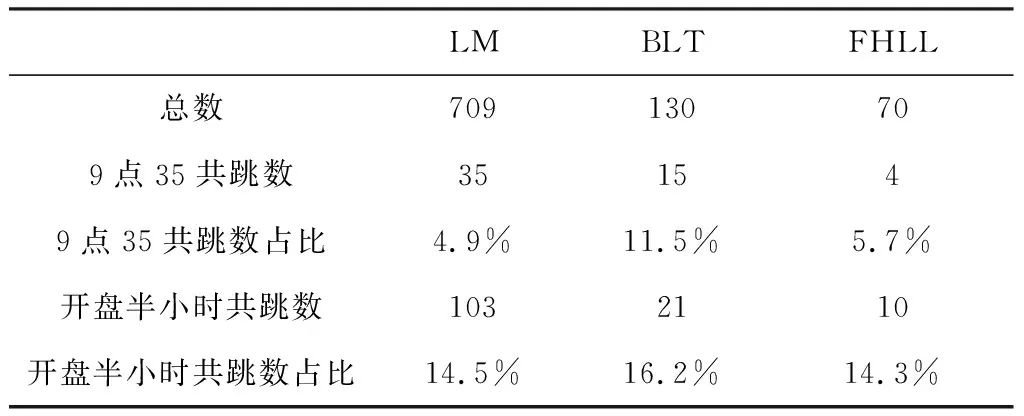
表5 不同共跳检验方法结果

三种方法中，检验共跳数量最多的是LM方法，其次是BLT方法的130次，最少的是FHLL方法的70次，BLT和FHLL方法的本质类似，由于FHLL利用了更多的数据，且其检验统计量的渐进方差最小，因此结果有所减少。

从三者的共跳时间分布来看，第一个检验点9点35分所占比重最大的是BLT方法，为11.5%，最小的是LM方法，为4.9%，但是除FHLL共跳外，其他两种方法9点35分共跳数量是所有时间段中最高的，且要明显大于其他时间段。10点之前的共跳比例最高的依然是BLT方法，为16.2%，最少是FHLL方法，为14.3%。从三种检验方法结果来看，每个交易日开盘时刻以及交易最初半小时是共跳发生频率较大的，说明市场在开盘阶段，协同运动效应是最明显的，这可能是由于市场开盘阶段要对一些宏观经济信息以及非交易时间的隔夜信息进行反应。

本文对三种方法检验共跳的重合部分进行了研究，并统计了重合共跳个数占各种方法的比例：

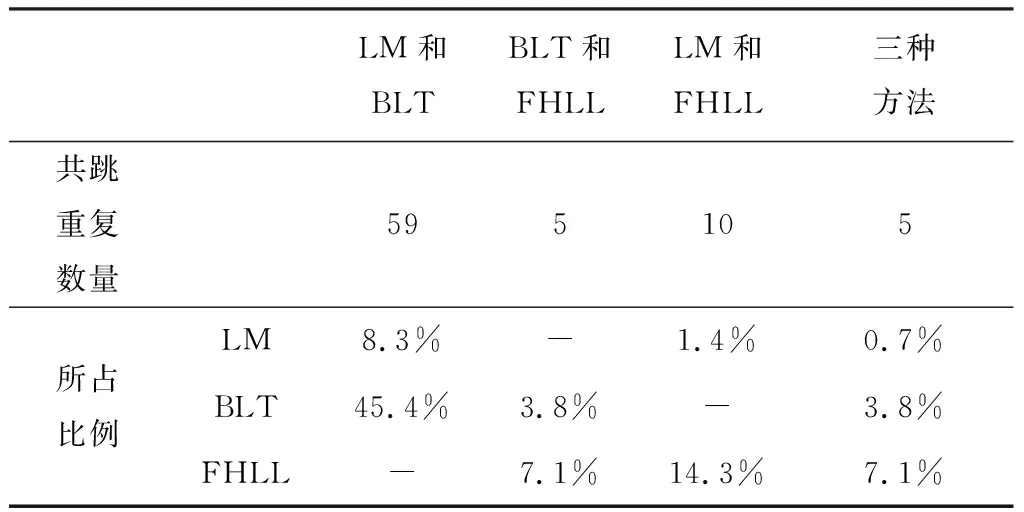
表6 不同共跳检验重合情况

对比结果显示，BLT和FHLL、LM和FHLL的重合时间均较少，为5次、10次，而BLT和LM的重合时间较多，为59次。从比例上来讲，LM与其他两种方法重合部分分别是8.3%、1.4%，BLT和其他两者重复分布分别为45.4%、3.8%，FHLL与其他两种方法重合部分分别占到7.1%、14.3%。总体而言，由于LM共跳数量最多，导致与LM共跳重复的比例占其他共跳比例较高，但占LM自身比例较少，虽然BLT检验方法和LM不同，但是利用的数据都是收益数据，因此两者的重合率较高，而FHLL方法与其他两者的重合率较低。在检验的时间范围内，有5次共跳是三种方法同时检验到的，具体时间如下：

表7 三种共跳检验重合时间

在LM共跳检验分析时，本文对20只以上股票同时跳跃的时刻进行了分析，其中包括了上述共跳重复时间中的2015年1月19日、2015年10月8日和2015年6月4日，这三个交易日市场波动明显。2014年11月17日是沪港通正式开始交易的时间，受此影响，上证综指高开随后又迅速下降，导致开盘阶段波动明显，LM共跳检验显示有8只样本股发生跳跃，2015年5月21日上证综指上涨1.87%，但没有发现其他异常情况。因此，在5个重复共跳时刻，有4次市场有明显的波动行情，这说明三种共跳检验都能够检验到市场的异常波动，只是各种方法在处理数据和利用的数据结构上存在差异，导致不同方法对异常波动的敏感性不同，因此大部分检验结果在时间存在不一致性。

4 Hawkes过程与泊松过程

对跳跃研究的主流观点认为，跳跃项是复合泊松过程。“泊松跳”有两个基本假设，一是单个资产跳跃和跳跃之间是独立的，二是不同资产之间的跳跃是独立的。然而，越来越多的证据表明，无论是单个资产还是资产组合之间的跳跃都呈现出和泊松跳不一样的特点。个股跳跃发生的密度呈现出明显的聚集性，有些时间内跳跃很少，有些时间内发生跳跃之后会接着发生多次跳跃。另外一个和泊松跳假设不符的现象就是共跳。前文用不同的方法证实了共跳存在的普遍性，过去的2015年，中国股市上演了多次的千股涨停和千股跌停，综合指数在短时间内有很大幅度的下挫，而创业板更是经历了多次指数跌停，这些现象都说明市场的融合性在不断提高，多个资产之间的同时性、同方向、大幅度的价格跳跃现象越来越多，这些同时性问题显然是违背每个资产的跳跃是独立的泊松跳的假设。

根据Bormetti等[13]的方法，本文将同一只股票在一段时间窗口内至少有两次跳跃的事件定义为MJ(Multiple Jump)事件，本文用下面的估计量来表示MJ事件的概率：

(25)

其中，N表示总的时间长度，w表示选择的时间窗口长度，⎣N/w」表示N/w的整数部分，Ιsi≥2是一个指示性函数，当一只股票在选定的w窗口内至少发生两次跳跃时，该函数取值为1，否则为0。这个估计量很好地反应了个股跳跃的聚集性，另一个类似的事件可以描述不同股票之间的共跳情况，本文将这个情况定义为CJ(Cross Jump)时间，同样有：

(26)

本文首先检验泊松跳的假设，如果认为个股的跳跃是相互独立的泊松跳，那么根据泊松跳的性质，上述两个估计量的均值方差计算如下：

(27)

其中，pw,λ=P({s≥2})=1-eλω(1-λw)，λ是泊松过程的密度。对于CJ估计量，类似有：

(28)

其中，qw,λt=P({si≥1})=1-eλiw。

根据中心极限定理，MJ统计量的分布近似于正态分布，可以根据正态分布计算临界值。

对于本文选取的50只样本股MJ统计量计算结果，在时间长度从10分钟到240分钟(即一个交易日的时间)跨度中，有47只股票实际计算出的MJ统计量均落在了99%临界值之外。三个例外个股情况分别是600009、600362、000983，但是，50只股票在最长100分钟的时间跨度中，所有股票的结果都不符合泊松跳的假设。因此可以得出结论，这些个股的跳跃不可能来自于泊松跳跃。

既然个股跳跃不符合泊松过程，就需要一个更为合适的模型去描述资产价格的跳跃，然后利用实证数据去验证这个过程是否较泊松过程更为有效。一个直观的想法是，可以放松一些泊松过程的假设条件，比如非齐次泊松过程，考虑到实证数据中一个跳跃可能激发另一个跳跃，本文采取了Hawkes过程作为代替泊松过程的点过程，这类过程的特点是密度是随机的、时变的，当一个跳跃发生之后，跳跃强度倾向于增大。

考虑单个点过程N(t)，如果该过程的密度满足以下条件，称之为Hawkes过程：

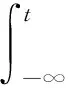
(29)

本文参考Ozaki的算法，采用极大似然估计方法估计参数。由于篇幅限制，这里对极大似然函数和参数估计结果等省略，有需要的可以和作者索取。在参数估计的基础上，利用算法模拟Hawkes过程，将上述参数带入模拟算法，得到结果，在结果的基础上计算MJ统计量。在模拟Hawkes过程时，本文参考Ogata[23]、Ozaki[24]等关于点过程模拟的算法。

从计算结果看，在Hawkes过程的假设下，在较小时间间隔下，大部分MJ统计量已经在99%置信区间内，随着时间间隔的增大，MJ统计量完全落入了99%的置信区间内，说明单变量Hawkes比泊松过程更好地描述个股跳跃的聚集性特征。

既然Hawkes过程能够很好地描述个股跳跃的聚集性，那是否可以描述多只股票跳跃的互激性呢？本文计算了数对股票的CJ统计量，利用模拟算法模拟1000次每对股票在Hawkes跳跃假设条件下的CJ统计量，然后计算99%置信区间，结果显示，独立的多维Hawkes过程不能描述多只股票之间的互激性，以000623、600030股票为例，结果显示，所有时间间隔长度下，CJ统计量均不在99%置信区间内，实证结果的CJ统计量要显著大于独立Hawkes假设条件下的模拟值。独立的Hawkes过程难以描述个股跳跃之间的聚集性，是否可以设立多维Hawkes过程，通过设置互激参数来描述多只股票跳跃之间的关系？

考虑K维Hawkes过程，多维密度为I(t)=(I1(t),…,IK(t))'，第k种资产的密度可以表示为：

(34)

上式中，所有的参数都是非负的，保证该过程的平稳性，参数矩阵

(35)

其值应小于1。参数αkk、βkk表示第m种股票价格路径的自激性参数，其余2K(K-1)个αkm、βkm表示第m种股票价格跳跃对第k种股票价格的互激参数。可以计算，当只有2种资产时，需要估计的参数是10个，K种资产则需要估计K(2K+1)个参数，数量较大，因此本文放弃多维Hawkes过程的假设。

5 Hawkes因子模型及其参数估计

5.1 泊松框架下的因子模型

参照Bormetti等[13]的研究思路，本文先建立一个“虚拟”因子模型，以阐述因子模型的主要思路，并说明因子模型在描述多只股票跳跃关系的优势。假设在市场中存在一个不可观察的因子，这个因子可以用一个点过程来描述。当这个因子发生跳跃，即代表市场因子的点过程发生跳跃时，不同的个股会依照各自特有的概率而发生跳跃。先考虑由两种股票S1、S2组成的市场组合，当市场因子跳跃时，股票S1有p1的概率会发生跳跃，股票S2有p2的概率会发生跳跃。当因子不发生跳跃时，这两只股票价格均不会发生跳跃，但是，如果观察到两只股票都没有发生跳跃，并不说明市场因子没有发生跳跃。本文用密度是λF的泊松过程表示市场因子，总时间长度为T，则因子发生跳跃的期望为λFT。个股跳跃和因子跳跃数之间的关系如下：

p1λFT=n1

(36)

p2λFT=n2

(37)

p1p2λFT=n12

(38)

其中，n12表示两只股票观察到的共跳数量。上述方程式中，前两个式子要求个股实际发生的跳跃数量和期望发生的跳跃数量相等，而最后一个式子保证了观察到的共跳和理论上共跳的期望值相同。n1、n2、n12、T都是已知量，未知参数可以表示为：

(39)

(40)

(41)

以000623、600030两只个股为例，000623发生了78次跳跃，即n1=78，600030发生了99次跳跃，即n2=99，两只个股同时跳跃的数量为24次，即n12=24。根据上述模型的假设，可以计算得出λF=0.0092，p1=0.24，p2=0.31。

在上述计算结果的基础上，首先模拟1000次密度为λF的泊松跳跃过程，在每一次模拟结果的基础上，加入符合二项分布的个股跳跃数据，然后得出每一次因子跳跃之后两只个股的跳跃情况，根据跳跃情况计算出CJ统计量的值，综合多次模拟结果计算出CJ统计量的均值和99%置信区间。从计算结果可以看到，泊松因子模型假设下CJ统计量都落在了模拟均值的附近，说明因子模型能够很好地描述股票跳跃之间的关系。但是，基于泊松过程的模型假设与实际情况不相符，泊松跳的假设不能很好地描述个股跳跃的聚集现象；另外，上述模型假设资产价格所有跳跃均来自于因子跳跃，不能发生特异性跳跃。

5.2 基于Hawkes过程的因子模型

本节将构建基于Hawkes过程的因子模型。在泊松因子模型中，假设存在一个不被观察的市场因子，而在Hawkes因子模型中，首先需要找到一个能够代表市场的因子的“事件”。怎样的事件才能代表市场因子，最明显的是当所有股票全部跳跃时，几乎可以肯定这时发生了系统性“事件”，可以认为是市场因子在发挥作用。但是，本文之前对50只样本股的跳跃实证检验说明，全部股票同时跳跃的事件是极其罕见的，最多观察到42只股票同时跳跃，这种现象发生在首个熔断机制触发之后的第一个交易日的首个交易时间段。当然，因子事件的识别也不能基于太少股票同时发生跳跃，比如2只股票，2只股票同时发生跳跃的次数共发生了709次，不能排除有一些2只股票共跳是“偶然发生的”。因此，本文将“因子”事件定义为3只或以上股票同时发生跳跃。

Ρ(Ns(t)在时间[t,t+Δt]发生跳跃t)=Is(t)Δt

(42)

其中，Ρ代表在长度为Δt的时间内，该计数过程在历史信息t的基础上发生跳跃的概率。假设样本股复合N维独立的Hawkes过程，前文已经通过极大似然估计计算出相应的参数值，然后针对共跳因子出现的时间，可以计算出个股在这些时间(设为t=1,…,TF)内跳跃的概率矩阵：

(43)

如果这些个股符合独立Hawkes过程的假设，可以计算在每个因子时间点，这些股票中恰好有3只股票同时发生跳跃的概率：

(44)

(45)

这样就得到了个股特异性跳跃的时间点和因子事件的时间点，然后可以通过极大似然估计重新对这些跳跃时间进行参数估计，以确定因子事件参数λF、αF、βF，以及个股特异性参数λs、αs、βs。

和之间泊松因子模型类似，当因子事件发生时，个股不一定全部跟着跳跃，跳跃与否和各自的概率ps有关:

(46)

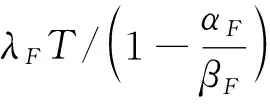
下面针对以上模型设定进行实证分析。在35只样本股中，3只股票或以上同时跳跃情况有172次，本文计算了这172次的Ρ(Jt=3)的值，剔除了其中23次概率值大于0.01的情况，最终确定149个因子事件，然后对因子事件和个股特异性跳跃进行参数估计。由于篇幅限制，这里参数估计结果等省略。有需要的可以和作者索取。

在参数估计的基础上，本文通过蒙特卡罗模拟来计算前文中的MJ、CJ统计量的均值及99%的置信区间。在模拟时，每只个股的总跳跃由两部分构成：一是特异性跳跃，二是以一定概率跟随因子事件的跳跃。首先利用因子事件的参数模拟出因子跳跃发生的时间，然后通过个股各自的ps值确定由因子事件产生的跳跃，随后利用个股的跳跃参数模拟出特异性跳跃，将两种跳跃取并集，得到个股跳跃的一次模拟结果，最后将上述模拟过程重复1000次。

本文选取了具有代表性的四只个股:000538、300024、000623、600030。其中，000538和300024的ps值较小，分别是0.09、0.06，000623和600030的ps较大，分别是0.13、0.17。本文计算了四只个股的MJ统计量，并通过模拟计算了相应的均值和置信区间。计算结果显示，在小于100分钟的较小时间间隔内，四只个股的MJ统计量基本落在99%置信区间内，有个别时间间隔在置信区间外，如000538，有些个股的MJ统计量基本在模拟均值附近，如600030。当时间长度大于100分钟时，所有个股的MJ统计量都在99%置信区间内。这和独立Hawkes假设条件下得出的结果基本一致，说明因子模型能够很好地描述个股跳跃的聚集性。

本文计算了两对个股的CJ统计量：000538和300024、000623和600030，前对组合特异性跳跃数、共跳数和ps值均小于后面的组合，这样的组合选择可以研究在不同参数组合情况下因子模型是否稳健。计算结果显示，第一组组合的CJ统计量都落在了均值附近，第二组组合在小时间长度下，CJ统计量在99%置信区间的边缘，当时间长度大于100分钟时，完全落在置信区间内，其他股票组合的结论与此类似。总的来看，因子模型能够解释多只股票共跳之间的同时性关系，但对互激关系较为密切的股票组合且时间窗口长度较小时，模型解释力要弱于其他股票组合，具体成因还有待进一步研究。

6 结语

本文选取了三种共跳检验方法对共跳进行了研究，LM检验方法识别的共跳数量最多，达到了709次，占数据总量的2.03%；BLT检验方法识别了130次共跳，而FHLL检验方法识别出70次共跳。从共跳日间时间分布情况来看，尽管剔除了数据的日间效应，三种方法结果都显示开盘时间的共跳数量是最多的，开盘半小时内的共跳数量占到所有共跳的15%左右。LM共跳检验结果显示，同时有超过20只个股共跳的情况基本都发生在市场有剧烈波动的情况下，其他两种共跳检验也捕捉到了一些剧烈波动，三种方法在检验时间上有5个时间点是重合的，这些时间点主要是市场处于暴涨暴跌行情时，另外，2016年首个熔断机制触发后的交易日时间也被三种方法识别为共跳，本文称之为“熔断共跳”。总体而言，三种方法对于市场较大波动的情况都能有效识别，但LM方法由于利用了个股跳跃结果，能够识别更多的市场波动，BLT方法和FHLL方法对于共跳识别较为谨慎， BLT方法与LM方法都只利用了收益数据，因此重合率较高，而FHLL方法利用了更多数据，与其他两种方法识别结果的重合率较低。但对于不同特征高频数据，由于微观噪声影响，通过LM方法识别的共跳可能是由于噪声的干扰，存在“伪共跳”，而BLT方法通过CP(Cross Product)统计量估计协方差也并不一定是最好的选择。FHLL方法对于共跳识别较为谨慎，利用了更多数据，对协方差估计更有效。但是FHLL方法对中等大小的共同跳跃更敏感。

引入Hawkes过程能够较好地描述个股跳跃的聚集性，通过对个股跳跃聚集性的MJ统计量和个股共跳聚集性的CJ统计量的计算发现，泊松跳的假设和实证数据相差较大，在假设个股跳跃符合Hawkes过程的基础上，50只个股中有35只个股的相关参数是显著收敛的，而且Hawkes假设下的MJ统计量计算结果与实证结果相吻合，但CJ统计量的计算结果说明独立的Hawkes过程不能描述共跳的聚集性，而多维Hawkes过程的推广又存在待估参数过多的问题，因此本文建立基于Hawkes过程的因子模型，在特异性跳跃的基础上，当市场因子跳跃时，个股依据不同的概率跳跃。本文将3只及以上个股的共跳作为市场因子事件，并剔除了此类事件发生概率较高的时间点。对因子参数和个股参数的估计结果显示，市场因子参数是显著收敛的，35只个股中有30只的参数是显著收敛的，且基于模型的MJ统计量、CJ统计量和实证数据的拟合程度较好，说明因子模型能够更好地描述跳跃和共跳的聚集性。