基于k值优化VMD的滚动轴承故障诊断方法*

王奉涛， 柳晨曦， 张 涛， 敦泊森， 韩清凯， 李宏坤

(大连理工大学机械工程学院 大连，116024)

引 言

滚动轴承是旋转机械中最易出现故障的零部件之一，其运行状况对设备的正常运转具有重大影响[1]。在滚动轴承失效前，对其进行故障诊断可有效避免后续事故的发生，最大限度地减少损失[2]。据相关资料统计，由振动故障导致的机械故障占70%，其中滚动轴承故障占据振动故障的30%[3]。现代设备日益高端化、自动化和精密化，对设备可靠性和预防维护的要求也日益提高。有效的故障诊断不但可以减少停工次数、降低维修成本，而且可以保障整个设备的正常运行[4-6]。

以傅里叶变换为基础的传统振动分析方法针对平稳信号取得了很好的效果，但是针对噪声干扰下的非平稳、非线性信号难以满足工程需求。经验模态分解(empirical mode decomposition,简称 EMD)与局域均值分解(local mean decomposition, 简称LMD)属于现代信号分解方法，得到广泛应用，但其递归模式分解会导致分解时的估计误差不断传递，出现模态混叠等现象[7-8]。此外对于相近频率的难分解、端点效应、过包络、欠包络、受采样频率影响及缺乏数学理论基础等问题[9-11]，导致在分解不同的工程信号进行故障诊断时，效果差别很大。VMD[12]是一种新的自适应信号分解方法，它不同于EMD和LMD递归式分解估算模式，而采用非递归的理念框架，可有效克服上述问题，表现出良好噪声鲁棒性。马增强等[13]经VMD分解后选定分量重构信号，结合Teager 能量算子实现对滚动轴承故障特征的提取。郑小霞等[14]针对信噪比低的海上风电机组滚动轴承故障信号，经VMD分解实现了故障识别，并且明显优于EMD方法。VMD方法的分解效果受分解信号分量数k的影响，即分解过多或不足会都影响分析结果的准确性。因此如何在分解前选择适当的k值，是VMD广泛应用的关键。

峭度值是一种全局信号统计分析量，在噪声干扰较小的环境下能发挥对奇异信号敏感的异常响应特征作用，而在强噪环境下不能有效反应局域分量的变化情况。为了改进峭度在实际应用中的缺陷， Dwyer[15]提出了谱峭度(spectral kurtosis, 简称SK)法。谱峭度是频域的一个统计工具，可以把信号中非高斯成分度量，同时可以指出非高斯成分在频域的频带。这可以理解成对每一条谱线计算峭度值，搜寻是否有不平稳特征信息，若有则在频带显示它们的坐标。Antoni[16]引入峭度图(kurtogram)概念并提出了快速峭度图方法，使谱峭度得到迅速应用，但在信号信噪比较低或含有随机脉冲噪声等情况下容易失效，由此不断提出的改进方法成为研究热点。

VMD适用于分离多分量非平稳信号，快速峭度图方法能自适应选取参数的带通滤波器，有效抑制噪声干扰。基于两者优点，为准确选取VMD方法信号分解个数k，防止分解过分或不足影响故障诊断结果，同时提高信噪比，准确提取滚动轴承故障特征，笔者提出了一种基于k值优化VMD与kurtogram的滚动轴承故障诊断方法。首先，依据基于能量的k值优化选取准则对滚动轴承原始振动信号进行分解；其次，根据峭度准则通过选取能够反映故障特征的分量进行信号重构；最后，通过kurtogram选择合适的滤波器参数进行滤波后包络分析，分别通过模拟信号与试验信号验证该方法的有效性和实用性。

1 理论基础

1.1 变分模态分解

根据VMD非线性、非平稳性信号频率随时间变化的特性，把信号局部特征信息附加到瞬时频率上，将复杂信号分解为有限k个调幅调频(AM-KM)分量信号，其表达式为

uk(t)=Ak(t)cos(φk(t))

(1)

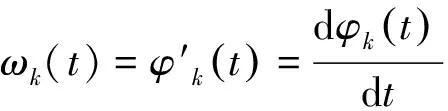
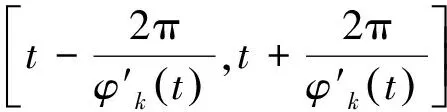
构建和求解变分最优解的过程涉及经典维纳滤波、希尔伯特变换和频率混合等过程，得到变分约束问题表达式为

(2)

其中：uk={u1,u2,…,uk}为各分量函数集；ωk={ω1,ω2,…,ωk}为各中心频率集；∂t表示对函数求时间t的偏导数。

引入二次惩罚因子α和拉格朗日惩罚算子λ(t)，经过傅里叶等距变换等过程得到

(3)

(4)

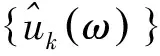
1.2 谱峭度理论

描述波形尖峰度的无量纲参数峭度，基本定义如下

(5)

其中：μ为正态分布的均值；σ为正态分布的标准差；E为变量期望值。

正常轴承的振动信号近似服从正态分布，其峭度值约为3[17]。当轴承出现故障时，峭度值明显增大。一般认为峭度值计算结果大于3的程度越大，则其含有的冲击信息成分越多；反之，则认为其故障冲击信号较少，一般舍弃不再分析。

假设Y(t)为由信号X(t)激励的系统响应，H(t,s)为时变冲击响应函数，那么Y(t)可写成

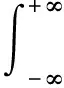
(6)

其中：H(t,f)为系统的时变传递函数；Y(t)为频率f处的复包络。

工程中，H(t,f)是随机的，可表示为H(t,f,ω)，ω表示滤波器时变性的随机变量。Antoni[18]对谱峭度深入研究后，给出对非平稳信号Y(t)的4阶谱累积量谱峭度定义。

滚动轴承一般的振动信号模型可表示为Z(t)=X(t)+N(t)，其中：Z(t)为采集的振动信号；X(t)为要检测的故障信号；N(t)为独立于故障信号的加性噪声。信号Z(t)的谱峭度可以表示为

(7)

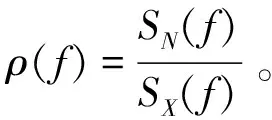
式(7)可以简写为

(8)

由式(8)可看出，在信号信噪比很高频率处，ρ(f)会很小，KZ(f)近似等于KX(f)；反之，在信噪比很低的频率处，即噪声很强烈时，ρ(f)会很大，最终KZ(f)趋向于0。因此，谱峭度法能够搜索整个频域，找到谱峭度最大的频带，即寻找故障信号X(t)。文献[16]提出基于滤波器组的计算方法的kurtogram，可以在很短时间内得到二维图，称为快速峭度图。

1.3 模态数选取准则

VMD分解结果中各分量是正交关系，因此从能量角度来说各分量的能量和与原信号的能量相等。VMD对噪声有很强的鲁棒性， 若VMD存在过分解，其剩余项的能量值在均值左右波动。若VMD的k值超过某一合适的值后，其过分解的分量是在原分量基础上分解出来的，由于存在虚构的分量，则多分解出来的分量能量线性之和应大于原被分解分量的能量和。基于此，笔者提出了一种从能量角度对VMD参数k的优化选定方法。

原信号或分量信号的能量计算公式为

(9)

其中：E为信号的能量值(原始信号或分量信号)；x(i)为信号序列；n为采样点数。

不同的信号分解的能量值大小不同，在本研究中定义分解能量差值参数η公式为

(10)

其中：Ep为对应的第p个分量的能量；Ex为原信号的能量。

由式(10)可知：过分解越严重，其值越大；而其值越接近或等于0，则分解合适或不足。

对一系列k值对应的能量参数η观察，当其值经过几个最低值(等于或接近0)后出现突变时，则此转折点参数对应的k就是最合适取值。

基本运算步骤如下：k值选择由2开始逐次增加，进行VMD预分解，分别计算参数η；当观察到参数η出现突变时即可停止，选择最后一个参数等于最低值时对应的k值，由此对原信号进行VMD分解。

2 方法步骤

本方法的具体流程图如图1所示。

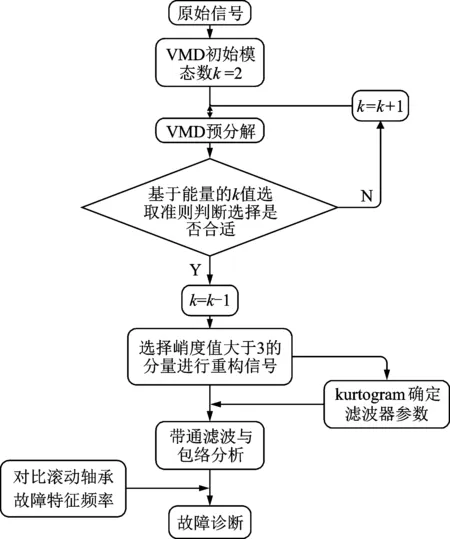
图1 方法流程图Fig.1 Flowchart of the proposed method

具体步骤如下：

1) 对加速度传感器采集得到的振动信号进行VMD预分解；

2) 根据基于能量的k值选取准则判断最终的模态分解个数；

3) 通过计算分量峭度值，筛选分量进行信号重构；

4) 通过kurtogram确定滤波器参数，对重构信号进行包络解调，分析频谱特征，确定故障类型。

3 仿真分析

构造多频信号叠加仿真信号，表达式如式(11)所示

(11)

VMD中参数值α取默认值2 000，采用的干扰信息为标准差为0.8的随机噪声。设采样点数为2 000，采样频率为1kHz，采样处理后的时域波形如图2所示。

图2 多频叠加信号时域图Fig.2 Time-domain of multi-frequency superimposed signal

由图2很难看出各信号特征，下面依次选取k值，通过模态数选取准则对原始信号进行预分解，结果如表1所示。

表1 仿真信号VMD各能量参数

原信号中由于存在模拟随机干扰，所以总能量值Ex存在波动。从表1可以看出：当k≤4时，其参数η均为0；从k=5开始，参数η逐渐增大，其走势图如图3所示。

图3 仿真信号参数走势图Fig.3 The trend chart of simulate signal

根据笔者提出的模态数选取准则可知，k=4为最优分解个数，由此分析VMD分解信号频谱特征，如图4所示。

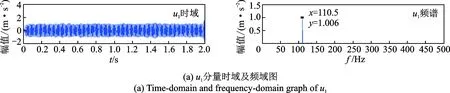
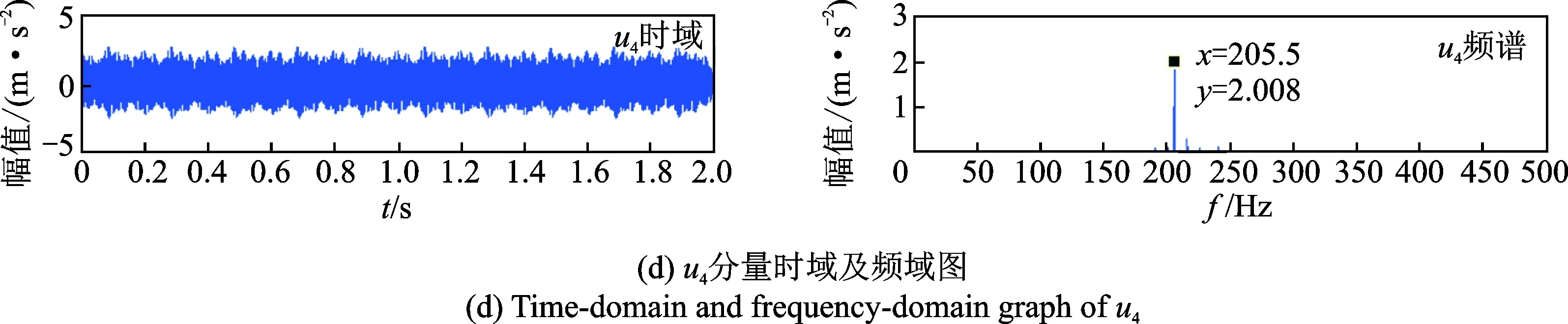
图4 仿真信号VMD分解各分量时、频域Fig.4 Time-domain and frequency-domain graph of simulate signal

由图4可以看出，经过VMD的分解信号u1，u2，u3，u4分别为110.5，145.5，180.5和205.5Hz的单信号，彼此之间没有干扰，各特征频率与原信号有0.5Hz的差别，均在允许误差之内。由此验证分解效果很理想，每一个分量均表现出了某一尺度范围的模态特性。

4 试验验证

试验装置由2个驱动电机、底台、支承机构、高压转子段、低压转子段及滚动轴承组成，如图5所示。

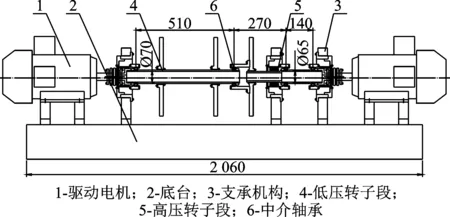
图5 试验装置机械结构示意图(单位：mm)Fig.5 The mechanical structure of the test rig(unit: mm)

试验轴承型号为NU1013，其中内圈与低速轴连接并随其旋转，外圈与高速轴连接并随其旋转，其主要技术参数如表2所示。

表2 试验轴承技术参数

采用电火花在试验轴承内圈滚道按轴线方向加工出深度为0.8mm的划痕，模拟内圈故障。采样频率为25.6kHz，采样点数为25 600，实测滚动轴承高速轴转速为600r/min(10Hz)，低速轴转速为-650 r/min(10.8Hz，转速方向与高速轴相反)，经理论计算可得该试验轴承内环的故障频率为239.7 Hz。

对加速度传感器采集得到的振动信号直接分析，由于信号传递路径、背景干扰等致使采集的信号信噪比低，很难在图6所示的时域波形和频域波形上直接做出准确诊断。频域波形上可以看到故障频率淹没在周围其他频率范围内，电压频率和转频等信号幅值大于故障特征频率，故障特征2及3倍频更是难以寻找，最终很难对轴承运行状态做出准确判断。进行包络谱处理后，如图7所示，转频20Hz以及其倍频幅值很明显，而内环故障特征频率难以找寻。

图6 原始信号时域波形和频域波形图Fig.6 Time-domain and frequency-domain waveform of original signal

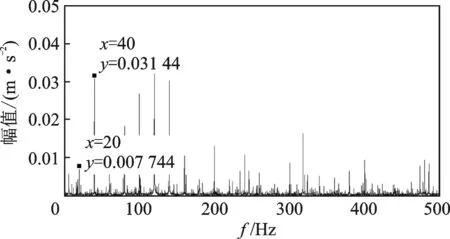
图7 原始信号包络谱Fig.7 Spectrum envelope of original signal

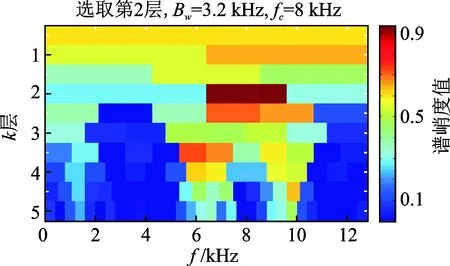
图8 原始信号快速谱峭度图Fig.8 The fast spectrum kurtosis graph of original signal

谱峭度法对振动信号有一定的处理能力，在采用本研究方法之前，先采用谱峭度法直接对原始数据进行快速峭度图处理，如图8所示。根据图上展示的最高谱峭度值0.9处，此时最佳组合(f/Δf)为[8 000，3 200]，即带宽Bw=3.2kHz，中心频率fc=8kHz。由此得到的带通滤波后的平方包络谱如图9所示。

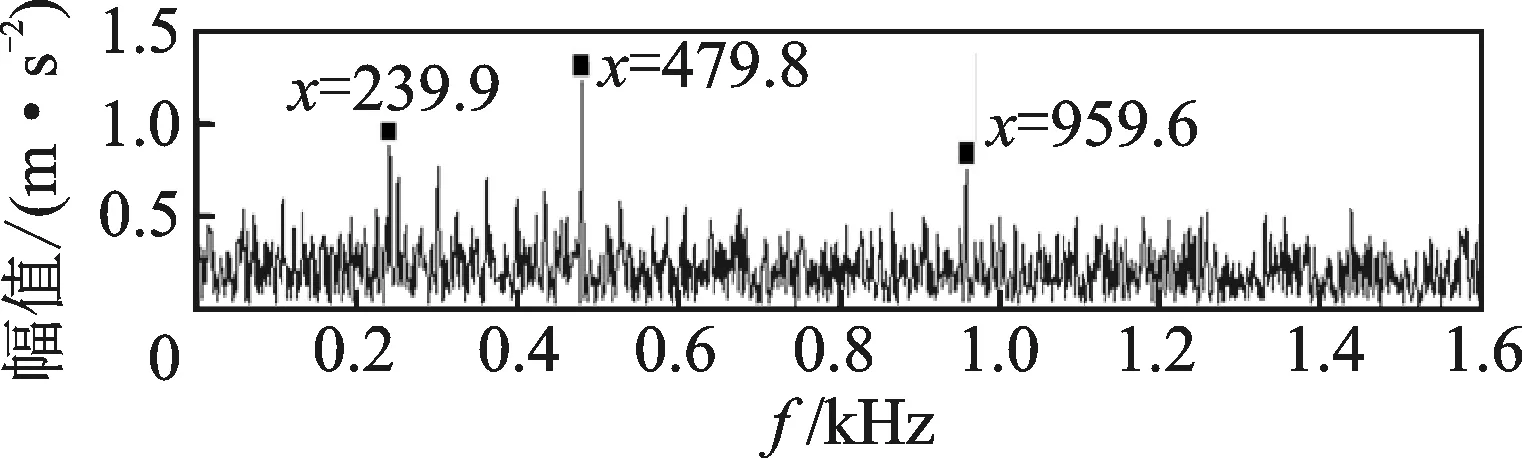
图9 原始信号平方包络谱Fig.9 The square envelope spectrum of original signal

由平方包络谱图可以找到故障特征频率的1，2和4倍频，其中2倍频最为明显，相对原信号直接频谱处理的结果，已经有很大的改善，还是存在不少干扰，1倍频周围的干扰幅值仍然很大，且明显小于2倍频。

采用笔者提出的方法进行分析。对加速度传感器采集得到的振动信号进行一系列VMD预分解，k值分别从2开始依次递增，每次分解均计算原信号能量值Ex和VMD各分量(包括剩余项)的能量值Ep，按照给出的式(10)计算其能量参数η，直至η出现较明显变化。所有分解计算结果如表3所示。

表3 试验信号VMD各能量参数

根据表3数据得到能量参数值的走势，如图10所示。

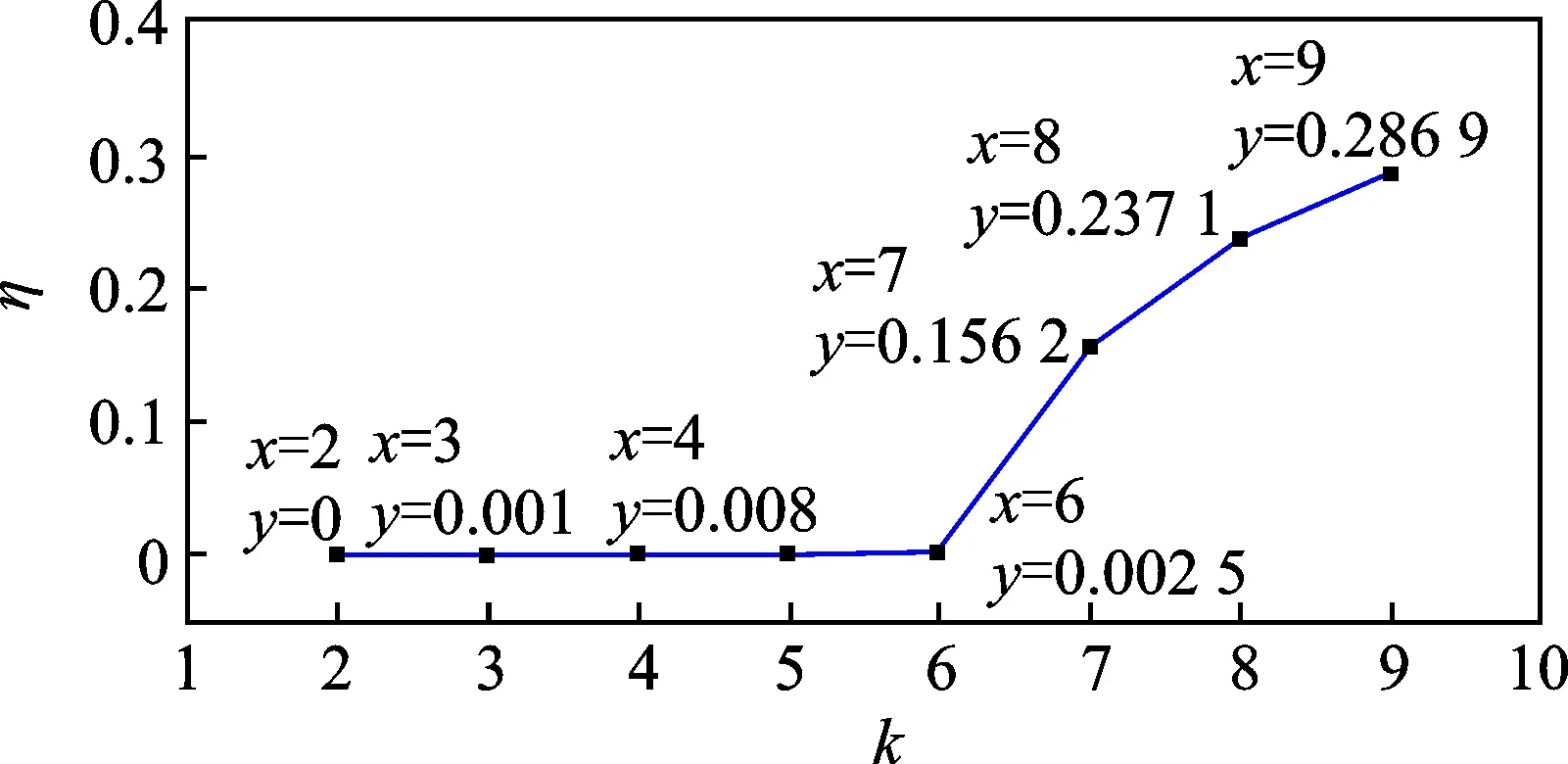
图10 试验信号参数走势图Fig.10 The trend chart of test signal

由图10看出，当k等于2时，参数为0，即分解前后能量差值为0；k取值从3～6时，虽然能量参数值出现0.000 8～0.0025之间的微小波动，但是变化范围相对很小，曲线较平稳，仍认为是在基值范围内；k等于7开始，能量参数值突增到0.156 2，随后不断增加。根据走势图可以看出，k等于6时曲线是走势变化转折点，按照模态数选取准则，认为此为VMD最优k值。由此分析此条件下VMD分解信号频谱特征，如图11所示。

图11 试验信号VMD分解各分量时、频域Fig.11 Time-domain and frequency-domain graph of test signal

分解得到的各时域图冲击比较明显，频域图中显示了对原信号从低频到高频的分解结果。根据峭度计算公式对分解的每个分量计算峭度值，如表4所示。

表4 各分量峭度值

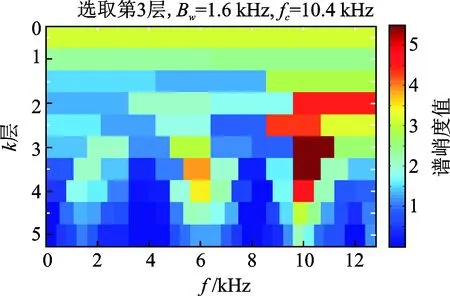
图12 重构信号快速谱峭度图Fig.12 The fast spectrum kurtosis graph of reconstructed signal

图13 重构信号平方包络谱Fig.13 The square envelope spectrum of reconstructed signal

由图13看出，振动信号中频率240Hz及其2，3倍频特别明显，甚至可以看到4倍频，几乎没有其他频率的混淆现象。对比滚动轴承故障特征频率，可以发现240Hz与内环故障特征频率极为接近。考虑到理论计算与实际的误差，可以判断是内环的故障特征频率，而且倍频突出，符合划痕故障的特性。由此可说明本方法在滚动轴承信号处理中效果很好，而且对提高信噪比效果突出。

5 结 论

1) 采用基于能量的k值优化VMD方法确定最佳模态数，能有效避免信号分解不足或过分解，为VMD方法在滚动轴承故障诊断中的应用提供了一种策略。

2) 采用VMD与kurtogram结合的方法诊断轴承故障，对重构信号进行包络分析，使得包络信号中故障频谱及倍频更加明显，能有效从背景噪声中分离出来。

参 考 文 献

[1] 王奉涛，王贝，敦泊森，等.改进Logistic回归模型的滚动轴承可靠性评估方法[J].振动、测试与诊断，2018,38(1):123-129.

Wang Fengtao, Wang Bei, Dun Bosen, et al. Rolling bearing reliability evaluation based on improved Logistic regression model[J].Journal of Vibration, Measurement & Diagnosis, 2018,38(1):123-129.(in Chinese)

[2] 郭红. 内外膜独立供油径推联合浮环轴承性能分析与实验研究[D]. 上海：上海交通大学, 2009.

[3] 何正嘉, 黄昭毅. 机械故障诊断案例选编[M]. 西安: 西安交通大学出版社, 1991: 14-18.

[4] Wei Guo, Peter W T. A novel signal compression method based on optimal ensemble empirical mode decomposition for bearing vibration signals [J]. Journal of Sound and Vibration, 2013, 332(2): 423-441.

[5] Cong Feiyun, Chen Jin, Dong Guangming. Vibration model of rolling element bearings in a rotor-bearing system for fault diagnosis [J]. Journal of Sound and Vibration, 2013, 332(8): 2081-2097.

[6] 王奉涛，陈守海，闫达文，等.基于流形-奇异值熵的滚动轴承故障特征提取[J].振动、测试与诊断，2016,36(2):288-294.

Wang Fengtao, Chen Shouhai, Yan Dawen, et al. Fault feature extraction method for rolling bearing based on manifold and singular values entropy[J].Journal of Vibration, Measurement & Diagnosis, 2016,36(2):288-294.(in Chinese)

[7] Huang N E, Shen Zheng, Long S R. A new view of nonlinear water waves: the Hilbert spectrum [J]. Annual Review of Fluid Mechanics, 2003, 31(1): 417-457.

[8] Yang Yu, Cheng Junsheng, Zhang Kang. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems [J]. Measurement, 2012, 45(3): 561-570.

[9] 任达千. 基于局域均值分解的旋转机械故障特征提取方法及系统研究[D]. 杭州：浙江大学, 2008.

[10] 程军圣, 郑近德, 杨宇. 一种新的非平稳信号分析方法-局部特征尺度分解法[J]. 振动工程学报, 2012,25(2): 215-220.

Cheng Junsheng, Zheng Jingde, Yang Yu. A nonstationary signal analysis approach--the local characteristic-scale decomposition method [J]. Journal of Vibration Engineering, 2012,25(2): 215-220.(in Chinese)

[11] Rilling G, Flandrin P. The influence of sampling on the empirical mode decomposition [C]∥IEEE International Conference on Acoustics Speech and Signal Processing Proceedings. Honolulu, HI, USA:[s.n.], 2006.

[12] Dragomiretskiy K, Zosso D. Variational mode decomposition [J]. IEEE Transactions on Signal Processing, 2014, 62 (3): 531-544.

[13] 马增强, 李亚超, 刘政, 等. 基于变分模态分解和Teager能量算子的滚动轴承故障特征提取[J]. 振动与冲击, 2016, 35(13): 134-139.

Ma Zhenqiang, Li Yachao, Liu Zhen, et al. Rolling bearings′ fault feature extraction based on variational mode decomposition and Teager energy operator [J]. Journal of Vibration and Shock, 2016, 35(13): 134-139.(in Chinese)

[14] 郑小霞, 周国旺, 任浩翰, 等. 基于变分模态分解的风机滚动轴承早期故障诊断[J]. 轴承, 2016(7): 48-53.

Zheng Xiaoxia, Zhou Guowang, Ren Haohan, et al. Incipient fault diagnosis for rolling bearings used in wind turbine based on variational mode decomposition [J]. Bearing, 2016(7): 48-53.(in Chinese)

[15] Dwyer R. Detection of non-Gaussian signals by frequency domain Kurtosis estimateon [C]∥IEEE International Conference on Acoustics, Speech, and Signal Processing .Boston, Massachusetts, USA:[s.n.], 1983.

[16] Antoni J. Fast computation of the kurtogram for the detection of transient faults [J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124.

[17] 苏文胜, 王奉涛, 张志新, 等. EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击, 2010, 29(3): 18-21.

Su Wensheng, Wang Fengtao, Zhang Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings [J]. Journal of Vibration and Shock, 2010, 29(3): 18-21.

[18] Antoni J. The spectral kurtosis: a useful tool for characterising non-stationary signals [J]. Mechanical Systems & Signal Processing, 2006, 20(2): 282-307.