一种基于奇偶判断WPT的多音干扰抑制方法*
2021-11-10章兰英任岱祥
章兰英 ,任岱祥
(1.航天工程大学,北京 102249;2.63770部队,西安 710600)
0 引言
卫星测控电磁环境日益复杂,测控设备面临的各种干扰日益严重,它的安全问题直接关系到航天器的可用性和生存能力。虽然扩频测控技术具有较强的抗干扰能力和较好的保密效果。但是,当信道中的干扰功率超过扩频增益所能提供的抑制能力时,扩频测控系统将不能满足系统正常工作的要求,整个测控系统的性能大大下降,严重时可能使整个测控系统失效,造成难以挽回的损失。因此在实际应用中,必须采取一定的信号处理手段来增强系统的抗强干扰能力。
依据干扰的频谱宽度与扩频信号的频谱宽度相对大小,扩频系统中的干扰可以分为窄带干扰和宽带干扰。高密度的窄带干扰[1-2](narrowband interference,NBI)是指所占频带宽度远远小于扩频信号带宽的干扰信号,它是破坏扩频测控系统的主要因素之一。变换域扩频信号窄带干扰抑制技术日益成熟[3-13],尤其是随着小波变换技术的发展,小波变换及其相应的滤波器组在窄带干扰抑制中应用广泛[3-11]。为了更彻底的滤除干扰,Pardo等提出采用频移非抽取性小波包变换(shifted undecimated wavelet packet transform algorithm,SUWPTA)来抑制窄带干扰[14-15],它首先将窄带干扰频移至最高分解层的子带中间位置,然后逐层分解至第一层,将干扰子带置零,以彻底滤除干扰。SUWPTA 方法简单,干扰抑制彻底,但是由于选择频移参数的判决准则和干扰子带判断准则均只适合单个窄带干扰的情况,不能抑制多音干扰。针对SUWPTA不能抑制多音干扰的问题,本文研究了基于奇偶判断的多音干扰抑制方法。通过对干扰子带编号进行奇偶判断,获得小波包自适应分解树,实现信号的自适应小波包变换和重构,最后通过仿真验证了该方法能够有效抑制多音干扰。
1 基于频移小波包变换的窄带干扰抑制方法
基于频移小波包变换的窄带干扰抑制框图如图1所示。

图1 基于频移小波包变换的窄带干扰抑制框图
假设接收到的信号为
r(n)=s(n)+i(n)+n(n)
(1)
式(1)中,s(n)为BPSK调制的扩频信号,i(n)为窄带干扰,n(n)为加性高斯白噪声。其中,扩频信号s(n)可以表示为:

cos[(ω0+ωd)nTs+φ]
(2)
式(2)中,P为接收到的扩频信号的功率,d(nTs)为二进制比特信息,c(nTs)为扩频码序列,ετ为接收扩频序列的伪码相位延迟,ω0和ωd分别为载波中心频率和多普勒频移。

1)频移小波包分解
频移小波包变换的窄带干扰抑制方法需要从最高层(第J层)开始分解的,首先将干扰平移至第J层的子带中间位置,这里采用子带能量差最大法来获得最佳频移量[10],即接收信号r(n)在频域每次向右滑动BJ/K,其中BJ为小波包分解最高层J对应的子带带宽,K为频移搜索次数,然后用第J层的滤波器H0,J(z)和H1,J(z)对其进行滤波,分别得到其低通子带信号W0,Sk(J)和高通子带信号W1,Sk(J),计算子带能量差。
ΔESk(J)=||W0,Sk(J)|2-|W1,Sk(J)|2|
(3)
当子带能量差最大时,干扰位于子带中间,此时对应的频移量为最佳频移量,即
S(J)={Sk(J)|max(ΔESk(J)),k=1,2,…,K}
(4)
小波包各层子带中心位置的变化情况如图2所示。
由图2可知,第J层高频子带的中心在第J-1层中的位置是高频子带和低频子带的交界处,而第J层低频子带的中心在第J-1层中的位置仍处于子带的中心。因此,频移后的信号通过第J层的滤波器H0,J(z)和H1,J(z)后,得到低通子带信号W0,J和高通子带信号W1,J,比较二者能量的大小即可判断出干扰位于低频子带或高频子带,从而得到小波包分解树。此时需要注意当干扰位于低频子带时,第J-1层可以直接对低频子带信号进行分解,而当干扰位于高频子带时,需要先将信号平移至第J-1层的子带中心,然后对频移后的高频子带信号进行分解,并保存不含干扰的子带信号和频移量,以此类推,直到将含干扰的信号分解到第1层。

图2 子带中心位置变化
2)NBI抑制
将含干扰的子带信号置零,滤除干扰。
3)频移小波包重构
根据保存的子带信号和频移量重构信号,得到不含干扰的信号。
对于单个的窄带干扰,频移小波包变换的窄带干扰抑制方法可以通过子带能量差最大准则将窄带干扰频移至子带中间。但是,当窄带干扰为多音干扰,子带能量差最大时,干扰并不是完全位于子带中间位置,并且当信号左右节点都存在干扰时,则不能通过子带能量大小来确定子节点是否继续分解,因此,频移小波包变换的窄带干扰抑制方法无法抑制多音干扰。
2 基于奇偶判断的多音干扰抑制方法
针对频移小波包变换的窄带干扰抑制方法无法抑制多音干扰的问题,本文提出了基于奇偶判断的多音干扰抑制方法,主要从最佳频移量搜索方法和干扰子带判断方法两个方面进行设计。
2.1 最佳频移搜索方法
在信号中存在多音干扰时,采用子带能量差最大准则来选择的最佳频移量,并不能保证将每一根多音干扰都频移至子带中间。经仿真发现,当干扰位于子带中间位置时,对信号进行小量频移时的子带能量是平稳变化的,如图3所示。
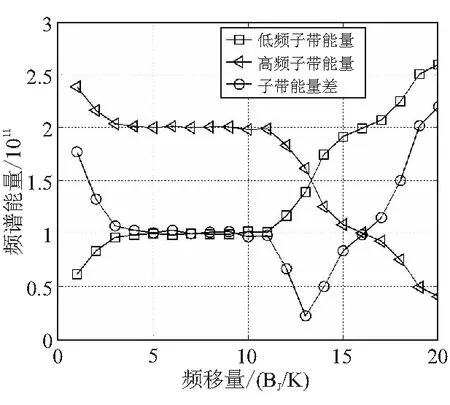
图3 子带能量变化情况
由图3可知,第5~10个频移步进时,干扰位于子带中间位置,对应的子带能量差变化平稳,而当干扰位于子带边缘位置时,由于子带滤波器对信号幅度的影响较大,子带能量变化波动较大,如图3中第11~20个频移步进时对应的子带能量差变化波动较大。因此可以采用子带能量差平稳度来选择最佳频移和最佳分解层数。子带能量差平稳度函数定义为:
PSk(J)=|ΔESk+1(J)-ΔESk(J)|+|ΔESk(J)-ΔESk-1(J)|
(5)
当PSk(J)最小时,说明各NBI均位于子带中间,子带能量差ΔESk(J)变化最平稳,此时对应的频移量为最佳频移量,即
S(J)={Sk(J)|min(PSk(J)),k=1,2,…,K}
(6)
通过子带能量差平稳度函数最小准则可以选择最佳频移量,频移后的信号中干扰位于子带中间位置,确保后续小波包分解。
2.2 干扰子带判断方法
通过子带能量差平稳度获得最佳频移量后,各NBI分别位于不同的子带中间。当信号中存在多个干扰时,如果左右节点都存在干扰时,将不能通过子带能量大小来确定子节点是否继续分解,为了便于小波包分解,本文提出了基于奇偶判断的干扰子带判断方法。
1)子带编号
为了便于跟踪干扰在子带中的变化,首先对各层子带进行编号,编号方式如图4所示。
由图4可知,在对第J层进行子带编号时,高频子带和低频子带连续编号,因此在第J层共有2J+1个子带。分解过程中,其余各层子带编号方式相同,第J层共有2J+1个子带。

图4 子带编号示意图
2)定位干扰

3)小波包自适应分解

(7)
假设当前信号中存在多音干扰的个数为n=3,最高分解层数为J=5,干扰对应的子带编号为{7,15,28},则根据式(7)可以得到一个J×n的干扰子带编号矩阵I

(8)
式(8)中,矩阵I的第1行表示在J=5层时含干扰的子带编号,第2行表示在J=4层时含干扰的子带编号,以此类推,直到第5行表示在J=1层时含干扰的子带编号,矩阵I的每一列表示某一根干扰在分解过程中所处的子带变化情况。根据I中各数的奇偶性得到干扰频带变化矩阵B

(9)
式(9)中,1表示奇数,说明干扰位于低频子带,0表示偶数,说明干扰位于高频子带,B中每一列表示,在小波包分解过程中某一根干扰在高、低频子带之间的变化情况,由此可以得到与B对应的小波包分解树如图5所示。

图5 小波包自适应分解树
图5中的(1,2,3)表示三根干扰,分别于B中列的序号相对应,小波包自适应分解树显示了每一根干扰在高、低频子带之间的变化,最后一层中的△表明该子带存在干扰,其中的序号为干扰的编号,与B中列的序号相对应。这种基于奇偶判断的干扰子带判断方法不仅能够很方便地得到小波包自适应分解树,还能够得到分解后的干扰子带编号,只需将含干扰的子带置零,就可以完成NBI的抑制。
因此,基于奇偶判断的多音干扰抑制方法采用子带能量差平稳度函数最小准则选择最佳频移量,并对频移后的干扰子带进行编号,根据小波包分解中的子带编号变化规律得到子带编号矩阵,通过对干扰子带编号的奇偶性判断很容易得到干扰的小波包自适应分解树。将含干扰的信号分解到第1层后,把含干扰的子带信号置零,滤除干扰,最后根据保存的子带信号和频移量重构信号,得到不含干扰的信号,完成多音干扰抑制。
由于单音干扰和窄带AR干扰只是信号中存在单根干扰,通过子带能量差平稳度同样也能够选择最优频移量,且对干扰信号的子带判断方法同样也能够适用于单根干扰的情况,因此基于奇偶判断的多音干扰抑制方法也可以用于对单音干扰和窄带AR干扰的抑制中。
3 多音干扰抑制性能仿真分析
下面通过性能仿真,从误码率、测速精度、测距精度三方面检验基于奇偶判断的多音干扰抑制方法的干扰抑制性能。
系统参数:采样率56 Msps,载波中心频率70 MHz,PN码为长1 023的gold序列,PN码速率5.115 Mcps,信息码速率5 Kbps,信干比SIR=-40 dB,载噪比52 dBHz,多音干扰频率为[-0.035 2π, 0.029 4π,0.317 7π]。
3.1 误码率仿真分析
下面仿真多音干扰下的误码率,误码率统计信息码元个数为105,载噪比变化范围40 dBHz~50 dBHz,对应解扩后信噪比变化范围0 dB~10 dB。图6中理论值为不存在干扰情况下,对BPSK进行相干解调的理论误码率值。
多音干扰情况下,干扰抑制后的解调误码率曲线如图6所示。
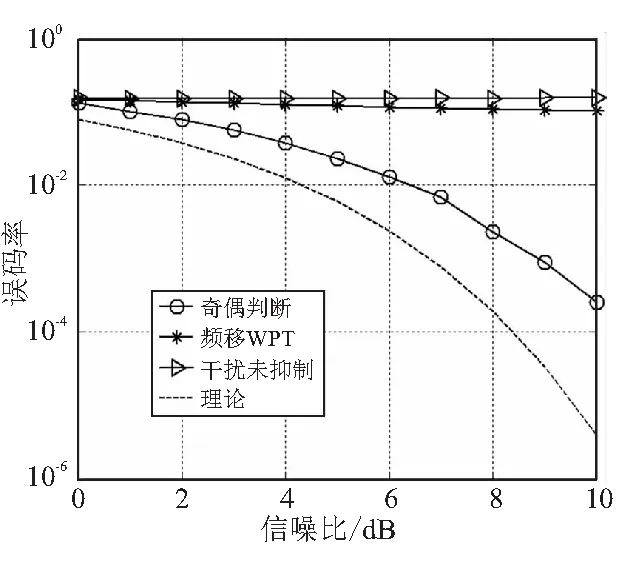
图6 干扰抑制后的误码率曲线比较
由图6可以看出,多音干扰情况下,基于奇偶判断的多音干扰抑制方法仍然可以正确解调信号,但是误码率比理论值要大,这是因为多音干扰占用的子带较多,采用小波包变换滤除干扰时对信号有用部分的损失较多,因此误码率有所增大。而频移小波包变换的窄带干扰抑制方法在多音干扰下,由于无法正确判断干扰子带的变化情况,不能抑制多音干扰,误码率很大,基本无法正确解调。
3.2 测速精度仿真分析
下面测试采用基于奇偶判断的多音干扰抑制方法进行干扰抑制后的测速精度,测速单元的积分平滑时间为0.05 s,蒙特卡罗仿真次数为10 000次。测试结果如表1所列。

表1 多音干扰抑制后的测速结果
由表1可以看出,基于奇偶判断的多音干扰抑制方法能够有效抑制多音干扰,干扰抑制后的测速精度能够满足指标要求。
3.3 测距精度仿真分析
下面测试采用基于奇偶判断的多音干扰抑制方法进行干扰抑制后的测速精度,蒙特卡罗仿真次数为10 000次。测试结果如表2所列。
由表2可知,基于奇偶判断的多音干扰抑制方法能够有效抑制多音干扰,干扰抑制后的测距精度能够满足指标要求。

表2 多音干扰抑制后的测距结果
通过以上基于奇偶判断的多音干扰抑制方法对多音干扰抑制后的误码率、测速和测距精度仿真可以看出,该方法能够有效抑制多音干扰。
4 结论
针对基于频移小波包变换的窄带干扰抑制方法无法抑制多音干扰的问题,提出了基于奇偶判断的多音干扰抑制方法,首先通过子带能量差平稳度函数最小准则选择最佳频移量,确保频移后的干扰位于子带中间位置,然后对频移后的干扰子带进行编号,通过对干扰子带编号的奇偶性判断得到干扰的小波包自适应分解树,根据分解树将含干扰的信号分解到第1层后,把含干扰的子带信号置零,滤除干扰,最后根据保存的子带信号和频移量重构信号,得到不含干扰的信号,完成多音干扰抑制。仿真结果表明,该方法能够有效抑制多音干扰。
