数学核心素养在例题教学中的渗透

☉甘肃省通渭县通和初级中学 张守荣 汤润华

《现代汉语词典（第6版）》对核心和素养是这样解释的：核心即中心，主要部分（就事物之间的关系而言）；素养即平日的修养.360百科和百度百科对核心的解释与其相同，但对素养均解释为通过训练和实践而获得的一种道德修养.无论是《现代汉语词典（第6版）》，还是360百科和百度百科，都没有对核心素养进行专门的解释，“核心素养”并不是核心和素养两个词的简单叠加，“核心素养”这个概念舶来于西方，英文词是“Key Competencies”.“Key”在英语中有“关键的”、“必不可少的”等含义.“Competencies”也可以直译为“能力”，但从它所包含的内容看，译成“素养”更为恰当.简言之，“核心素养”就是“关键素养”.结合数学学科特点，王尚志、史宁中等专家对数学核心素养给出了界定：数学核心素养是具有数学基本特征、适应个人终身发展和社会发展需要的必备品格与关键能力，是数学课程目标的集中体现，是在数学学习过程中逐步形成的.数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析共六个方面；共包含10个核心概念，即数感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力、模型思想、应用意识和创新意识.培养学生数学核心素养也完全符合“人人都能获得良好的数学教育，不同的人在数学上得到不同的发展”的要求.课堂是培养学生数学核心素养的主阵地.本文以人教版义务教育课程标准实验教科书八年级上册“13.3.1等腰三角形”的一道例题为例，对数学核心素养在例题教学中的渗透进行阐述.

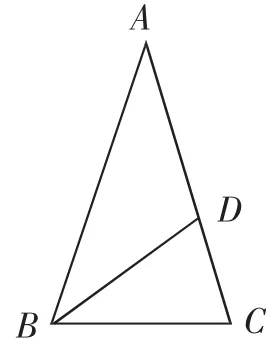
图1

一、理解例题，提高运算能力和推理能力

例题呈现：如图1，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数.

师：题中要求的是角的度数，但条件中只说了一些线段之间的相等关系，没有说出任何一个角的度数，我们从哪儿寻求突破？

生1：可以通过等腰三角形的性质把边相等转化为角相等.

师：请具体说一下.

生1：由AB=AC可以得到∠ABC=∠C，由BD=BC=AD可以得出∠C=∠BDC，∠A=∠ABD.

师：很好！虽然从题目条件来看并没有说任意一个角的度数，但是利用等腰三角形的性质，通过相等的边找到了相等的角，这样就为求出△ABC的各角提供了一种可能，但是只有这些关系还不够，还要寻找出这些角之间的其他关系.

生2：因为∠BDC=∠A+∠ABD，再由生1所说的几组相等的角可知，∠ABC=∠C＝2∠A.

师：这样我们就厘清了△ABC各角的关系，它们的两个底角相等，底角为顶角的两倍，现在如何求出这三个角？

生3：根据三角形的内角和为180°，再结合生2推出的三个角之间的关系，可知5∠A＝180°，最后可求得∠A＝36°，∠ABC=∠C＝72°.

师：这三位同学的分析和推理很棒，实际上我们把顶角为36°或者底角为36°的等腰三角形叫做黄金三角形，这里的△ABC实际上就是黄金三角形的一种，既然叫做黄金三角形，它自然和黄金一样弥足珍贵，大家一定要好好珍惜和研究这类三角形.

点评：这个题目对刚刚学习等腰三角形性质的学生而言并不难，部分学生能够迅速知道结果，但是在求三个内角度数的过程中，教师并没有要求让学生快速地求出结果，而是不急不徐地让多个学生来完成，生1完成了由等边到等角的转化，这样就把“由边求角”的“异类”问题转化为“由角求角”的“同类”问题，让学生慢慢体会转化思想，也符合“慢教育”规律.然后再由生2和生3分别通过三角形的任意一个外角等于和它不相邻的两个内角的和、三角形的内角和等于180°解决这个问题，这两个知识点由不同的学生说出，有利于后进生对知识的分化复习和理解，也有利于对本题的解决.在问题解决之后，教师“突然”给出教材中并没提到的黄金三角形概念，教师“仅仅”给出了概念，没有解释为什么要这样“称呼”，这个 “称呼”要在学习了相似之后来理解体会，教师在此处并没有多言，因此这个“陌生”概念不仅不会增加学生负担，相反反映出教师对学生“负担”的重视，这时提出让学生有更多的想象空间，“为什么叫做黄金三角形？会不会和黄金分割数有关？”在拓宽了学生的数学知识面的同时一下会激发学生的学习兴趣，学生感到这个题目不“简单”，为进一步研究埋下伏笔.

图2

二、寻找形似，形成空间观念和几何直观

师：请大家找一下，这个图形中共几个三角形？生4：共有三个，它们分别为△ABC，△BCD，△ABD.

师：这些三角形有什么特征？

生5：都是等腰三角形.

师：我们又把它叫做什么三角形？

生6：黄金三角形.

师：非常好，图1可以认为是作顶角为36°的等腰三角形的一个底角的角平分线，从而构造出了另一类黄金三角形.现在请大家先画一个底角为36°的等腰三角形，然后再想办法构造出另一类黄金三角形

生7：（生7把他的图形在屏幕上做了展示，为了和上图对比研究方便，把图2作了一定的技术处理，把原图的字母C和D作了交换，并且把原图中虚线都改成了实线，生7的部分叙述也改成和图2匹配的语言）我先画出底角为36°的等腰三角形△ABD，如果再在这个图形中画出顶角为36°的等腰三角形，只需把其中一个底角变成顶角就可以了，我把线段AD延长到点C，使AC＝AB，然后连接BC，就有△ABC为顶角为36°的等腰三角形，同时可知△BCD也为顶角为36°的等腰三角形.

师：生7做得非常好，通过这样一做，一下找出两个顶角为36°的等腰三角形.那么图1和图2一样吗？

众生意见不一.

师：看来意见还是不一样，谁发表一下自己的见解？

生8：一样，图2实际可以由图1绕点B逆时针旋转108°得到，所以这两个图形实际上是一样的.

师：从这两个图中可看出，两类黄金三角形可以互相转化而得出，它们遥相呼应.

点评：通过对图1的研究，学生有强烈的继续研究这个题目的意愿，教师抓住学生心理特点，继续挖掘例题资源，由于学生知识储备量的限制，教师只是引导学生去画图，然后，通过观察发现两个图形实际可以认为是同一个图形，目的就是让学生明白两个黄金三角形之间可以和谐地转化，感受到数学之间的和谐美和统一美，看似“多余”的研究恰好彰显教师的别出心裁.

三、追求神似，构建模型思想和应用意识

师：大家还有没有其他的办法来构造出另一类黄金三角形？

生9：我是在线段AB上截取AD=AC，然后连接CD，这样就有△ACD就是顶角为36°的黄金三角形，同时也可推出△BCD为底角为36°的黄金三角形.

师：生8是通过延长腰的办法把底角变成顶角找到另一类黄金三角形，这时我们可以想到在底边上截取和腰等长的办法来找到另一类黄金三角形，生9为我们想到了这个办法，多角度考虑问题是数学学习中非常必要的.那么，图3和图1、图2一样吗？

众生：（沉默片刻）一样.

生10：不一样，图3无法通过旋转得出.

师：无法通过旋转得出，那能否通过平移、翻折等变换得出？

众生：（沉默片刻）不能.

师：通过大家认真观察之后，图3和图1、图2并不是同一个图形，大家还能通过哪些办法说明它们不一样？

生11：图1、图2共有三个三角形，其中两个是顶角为36°的等腰三角形，一个是底角为36°的等腰三角形，而图3中一个是顶角为36°的等腰三角形，两个是底角为36°的等腰三角形，所以这两个图形自然不一样.

师：生11观察非常仔细，实际上这两个图形不一样，虽然它们不一样，但是我们可以认为它们形不似而神似，它们都由两类不同的黄金三角形组合而成.

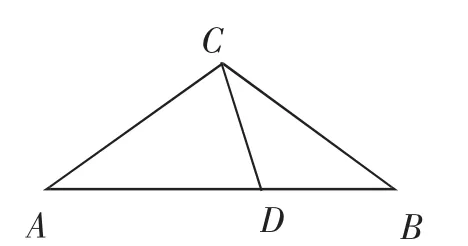
图3

点评：本以为在学生讨论出图1和图2后，对这个例题的研究会“圆满”收场，没想到教师完全没有停下来的意思.不断让学生在画图、观察中体会数学知识的生成过程，无形中完成了数学图形从有形到无形、从形似到神似的转化.这使我想起来了日本数学教育家米山国藏的一段叙述：学生在学校学习的数学知识，毕业后若没什么机会去用，一两年后很快就忘掉了；然而，不管他们从事什么工作，那种深深铭刻在心中的数学的精神、数学的思维方法、研究方法、推理方法和看问题的着眼点等，却随时随地在发挥作用，使他们终身受益.这里所说的“学校教育忘掉后所留下的”实际上就指的数学思想和方法，显然教者追求的是当他们走向社会忘掉数学知识后留下的“东西”.

四、拓展延伸，体验分类思想和归纳思想

生12：老师，我还有办法在底角为36°的等腰三角形中做出顶角为36°的等腰三角形，如图4所示（他向大家展示了所画图形）.

师：噢！不错啊！看来大家已经在这道题上“停”不下来了，不过相比前几个图形，这个图形“只有”两个三角形，大家可以在此基础上能“画”出更多的黄金三角形吗？

生13：延长AC、BC分别交BD、AD于点E、F，这样会出现好多黄金三角形（如图5）.

师：很好！那么图5共有多少个三角形？多少个黄金三角形？请同学分小组讨论出来.

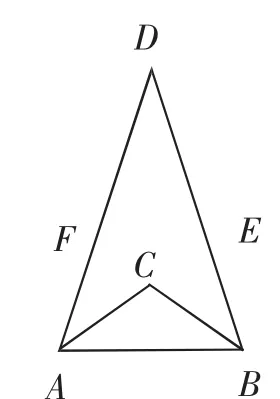
图4

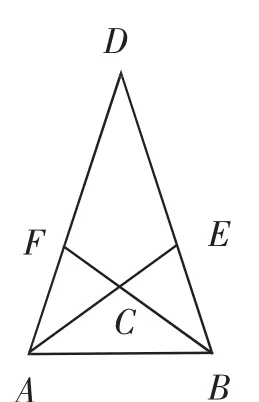
图5

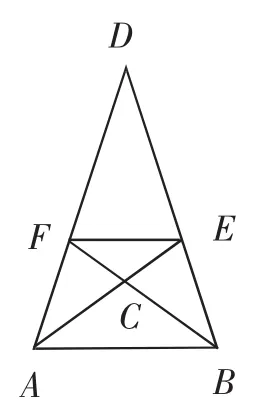
图6

（片刻之后）

生14：共有八个三角形，且这八个三角形都是黄金三角形.其中△ABD、△ACF、△BEC、△ABE、△ABF是顶角为36°的黄金三角形，△ABC、△AED、△BDF是底角为36°的黄金三角形.

生15：我们一组还把EF连接了，如图6，这时又增加了一些三角形，且这些三同样都是黄金三角形，多出来三角形的△DEF、△CEF、△AEF、△BEF，至于它们是哪一类黄金三角形不用我说了吧！（微微一笑）

老师：大家都这么棒！对于这样一个“简单”的例题竟然能找到这么多“资源”，在数学学习中一定要善于观察、善于总结，才有可能学好数学、用好数学.

点评：在讨论完前三个“图形”之后，看起来对于此类图形的研究已经完美了，教师也准备对这个例题收场，准备下一环节内容，但是生12让课堂“节外生枝”，学生牵着教师的鼻子走，老师也很“听话”地顺着学生的思路，并没有强行阻止或者强行总结学生的发言，索性再提出一些更有挑战性的问题 （不断地在生12给出的图形上加线），及时地让学生分组讨论，把学生的独立思考和小组合作结合的恰到好处.当讨论到这里时，距离下课还有三分钟，教师准备的教学内容显然无法完成，“必要”的课堂练习还没有做，表面看起来是结构不完整的一节课，但这些恰好说明“艺高人胆大”，教师很好地抓住生12的发现，让学生接着讨论，在寻找三角形时怎样找才能不重不漏，这体现了分类思想，然后把找到的三角形怎样归类，这又体现了归纳思想，这两个思想作为非常重要的数学思想方法，教师在教学中让学生做到完美的体验，真正做到了以生为本，注重对数学核心素养的培养和发展.

五、结束语

从例题展示的“黄金三角形”出发，先让学生求出三角形三个内角的度数，让所有的学生都体会成功的喜悦，并提高了学生的运算能力和推理能力，体现出运算能力和推理能力作为数学核心素养的基本要求.然后“话锋一转”，提出一系列“画图”问题，把所有的问题都转化为分析和观察图形，在图形中找出尽可能多的结论，同时提出的问题具有一定的开放性和挑战性，不同的学生会有不同的观察结果，自然会有不同的收获，然后集众人之力完善结论，在讨论过程中既有独立思考，又有小组合作，每个学生都体验到了空间观念和几何直观，同时还培养了学生的模型思想、归纳思想、分类思想以及数学的应用意识，而这些正好是数学素养的核心内容.

数学课堂是培养和发展学生数学核心素养的主阵地，例题教学自然也承载着重要的任务.但是核心素养不同于全面素养，核心素养必须是“核心”的素养，核心素养之外，还应该有“非核心素养”，因此仅凭一道例题不可能把数学核心素养的内容面面俱到，对于数学核心素养的形成不能一蹴而就，更不能照本宣科，一线教师能做的就是尽可能多地挖掘和发现教材资源，学习资源，让尽可能多的学生发展数学核心素养.