基于奇异值和奇异向量的振动信号降噪方法*

张晓涛， 李伟光

(1.广东机电职业技术学院汽车学院 广州,510515) (2.华南理工大学机械与汽车工程学院 广州，510640)

引 言

应用电涡流位移传感器非接触地测量转子轴颈处的振动位移可以实现对旋转机械工作状态的在线监测和故障诊断。因工作现场恶劣工作环境的影响，采集的振动信号中往往伴随着各种噪声干扰，而电源系统的工频噪声易耦合到信号中来，从而导致对旋转机械运行状态的误判。因此，降低和消除振动信号中的随机噪声和工频噪声干扰是旋转机械振动信号处理研究的重要内容。

SVD方法在振动信号处理领域有着广泛应用，如特征提取[1]、降噪[2-3]、提取信号中的周期成分[4]等。当用于振动信号降噪时，它将包含信号的矩阵分解为一系列的奇异值和奇异向量对应的正交子空间，选取有效的奇异值阶次进行信号重构可实现信号降噪。有效奇异值阶次直接影响信号的重构结果，因此其选取至关重要。典型选取方法是奇异值差分谱方法[5]，它依据差分谱中最大差分值所在位置来确定有效奇异值阶次，还有基于结构风险最小化原则的方法[6]、基于非监督动态聚类的方法[7]等。

SVD方法在降低工频噪声干扰方面有一定的应用[8-10]，且取得良好效果，但需满足工频分量对应的奇异值在奇异值谱中为最大值这一条件。在工程应用中，信号中与转子振动特征有关的分量通常是主要的，而工频分量则是次要的，所以奇异值谱中工频噪声分量对应的奇异值通常不是最大的，因而SVD方法在此方面应用时有一定局限性。

SVD方法在信号降噪和工频干扰消除方面的相关研究大都集中在奇异值本身，而未涉及奇异向量。实际上奇异向量包含丰富的信号特征信息，如梁霖等[11]对信号的连续小波变换系数进行SVD处理，选择反映信号特征的奇异向量进行重构以实现信号降噪。Groutage等[12]指出奇异向量包含信号的时频信息等。

仅从奇异值规律出发，SVD方法可以降低随机噪声和工频噪声，但存在上面提到的局限性。笔者将奇异值规律和奇异向量所含的特征信息相结合，提出了新的奇异值和奇异向量相结合的降噪方法，可有效克服这种局限性，既能降低随机噪声，也能降低工频噪声。首先，对信号作SVD，由奇异值规律确定有效奇异值阶次，从而降低随机噪声；其次，对该阶次范围内的奇异向量作FFT，筛选含工频及其倍频特征的幅值谱以得到对应的奇异向量，用其余的奇异值和奇异向量进行重构以得到时域信号，进一步降低工频噪声。应用仿真信号和工程试验信号对该方法的有效性进行验证。

1 基于奇异值和奇异向量的降噪方法

1.1 奇异值分解理论

对实矩阵A∈Rm×n，存在正交矩阵U∈Rm×m和V∈Rn×n，使得下式成立

A=UΛVT

(1)

其中：Λ为对角矩阵，其非零对角元素σ1,σ2,…,σr为Λ按降序排列的奇异值；r≤min(m,n)，r为A的秩。

由于Λ为对角矩阵，A可表示为r个秩为1的m×n阶子矩阵和的形式，如式(2)所示

(2)

其中：ui和vi分别为矩阵A的第i个左奇异向量和右奇异向量；σi为矩阵A的第i个奇异值。

由离散数字信号x(i)(i=1,2,…,N)可构造多种形式的实矩阵A，而Hankel矩阵是其中最常见的一种形式。当Hankel矩阵行数为信号长度的一半时，信号的分离效果最好[5]，本研究都采用这种结构的Hankel矩阵。

1.2 奇异值差分谱

若信号的奇异值序列表示为S=[σ1,σ2,…,σq]，q=min (m,n)，定义

bi=σi-σi+1(i=1,2,…,q-1)

(3)

则序列B=[b1,b2,…bq-1]被称为奇异值差分谱[5]，它描述了相邻奇异值的变化。文献[5]以平稳交流信号为例，将差分谱中最大峰值所在的位置确定为有效奇异值阶次，而在实际应用中，受现场工作环境影响或发生故障时，振动信号具有非平稳的特征[13]，因此需研究适用于非平稳信号的有效奇异值阶次选择方法。

奇异值同信号中各分量的能量有关，当有用信号的能量比噪声的能量大时，表征有用信号的奇异值同表征噪声的奇异值之间会产生突变，突变位置之前的奇异值对应于有用信号分量，突变位置之后的奇异值对应于噪声分量。以奇异值差分谱中从右往左的第1个极大值所在位置(即突变位置)为有效奇异值阶次，其他极大值则表示信号中各分量之间能量的变化。

1.3 基于奇异值和奇异向量的降噪方法

奇异值是纯实数，同信号中各分量能量有关，而奇异向量则包含信号特征信息，因此将奇异值和奇异向量相结合更为合理。由于各奇异向量波形差别不明显，而经FFT处理后所得频谱的区分度则较大，所以采用奇异向量的幅值谱为区分奇异向量的依据。基于奇异值和奇异向量相结合的振动信号降噪方法如下：

1) 振动信号作奇异值分解，生成一系列奇异值和奇异向量；

2) 以奇异值差分谱中从右至左的第1个极大值所在的位置为有效奇异值阶次；

3) 对有效奇异值阶次范围内的左(或右)奇异向量进行FFT，筛选具有工频及倍频特征的幅值谱以得到对应的奇异向量和奇异值，并用其余奇异值和奇异向量进行信号重构，结果即为所求。

2 数值仿真分析

用工频和变频相结合的信号f(t)来仿真非平稳振动信号，叠加高斯白噪声N(0,1)，信噪比为0.627 4

f(t)=sin(2πt+40t2)+sin (100πt)

(4)

含噪仿真信号的波形如图1所示，频谱如图2所示。

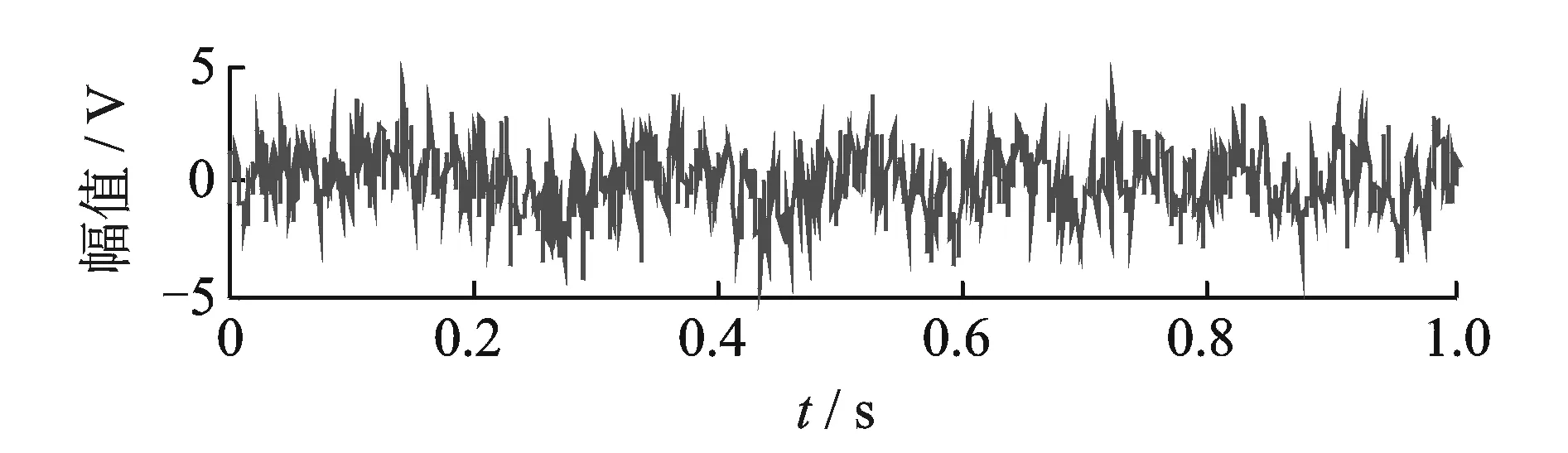
图1 仿真信号波形Fig.1 Waveform of simulation signal

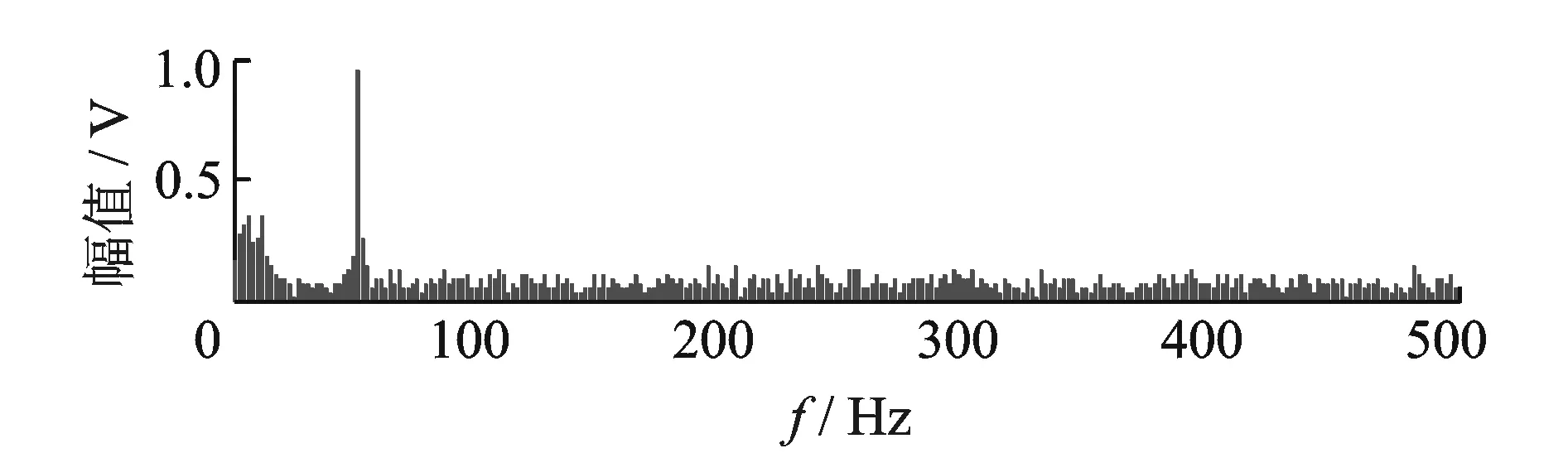
图2 仿真信号频谱Fig.2 Spectrum of simulation signal

仿真信号经SVD处理后得到的奇异值谱如图3所示，生成的奇异值总数为512。为突出显示奇异值谱中前面较大的奇异值，图3中只给出了第1个奇异值之外的前30值。由图4奇异值差分谱可见，从右至左的第1个极大值为第10个值(其值为120.213 7)，由此确定有效奇异值阶次为10，工频分量和变频分量对应的奇异值都集中在这范围之内，但具体的对应关系并不清楚。

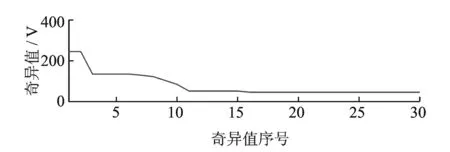
图3 仿真信号奇异值谱Fig.3 Singular values spectrum of simulation signa

图4 仿真信号奇异值差分谱Fig.4 Singular values difference spectrum of simulation signal

为研究奇异向量的性质，图5列出了前6个奇异向量的波形。为便于比较，将左、右奇异向量显示在同一个图中，左奇异向量ui为512点，用红色间断线表示；右奇异向量vi为513个点，用蓝色实线表示，采用左对齐的方式显示。

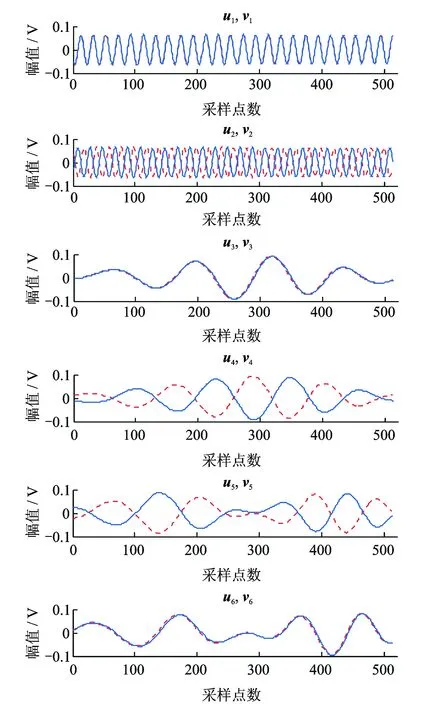
图5 仿真信号奇异向量波形Fig.5 Waveform of singular vector of simulation signal

由图5可见，同一奇异值的左、右奇异向量具有以下关系：完全重合(i=1,3,6)；或关于横坐标轴对称(i=2,4,5)，因此左、右奇异向量的FFT处理结果相同。左奇异向量u1和u2经FFT处理后得到如图6所示的频谱，u3经FFT处理后得到如图7所示的频谱，其他奇异向量频谱可同理得出。比较图6和图7的频谱可见，两个频谱完全不同，图6所示两个频谱都是50 Hz，ui(i=1,2)对应于工频分量；图7所示频谱位于更低的频段，ui(i=3)对应于变频分量。由奇异向量和奇异值的对应关系，奇异谱中第1，2个奇异值对应于工频分量。将第1，2个奇异值置零，并重构为时域信号，重构信号如图8所示。由图8可见，不但随机噪声被消除，而且工频噪声也得以消除，得到完整的变频信号。计算重构信号和变频信号的互相关系数，计算结果为0.882 0，这表明二者高度相关。

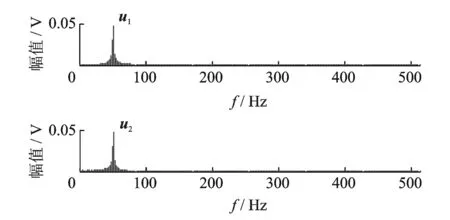
图6 左奇异向量u1和u2频谱Fig.6 Spectrum of left singular vectors u1 and u2

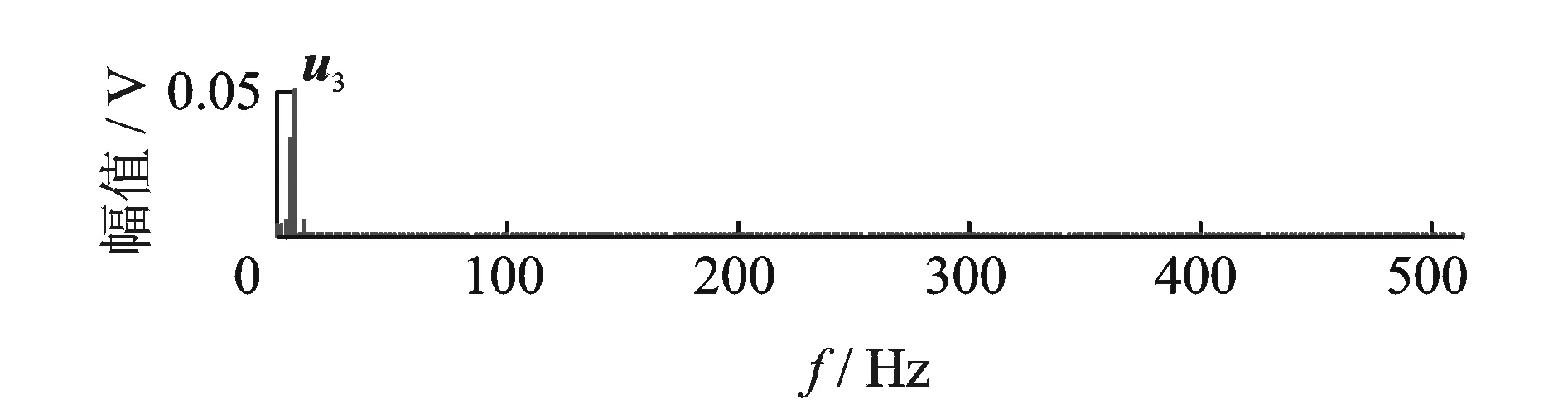
图7 左奇异向量u3频谱Fig.7 Spectrum of left singular vector u3

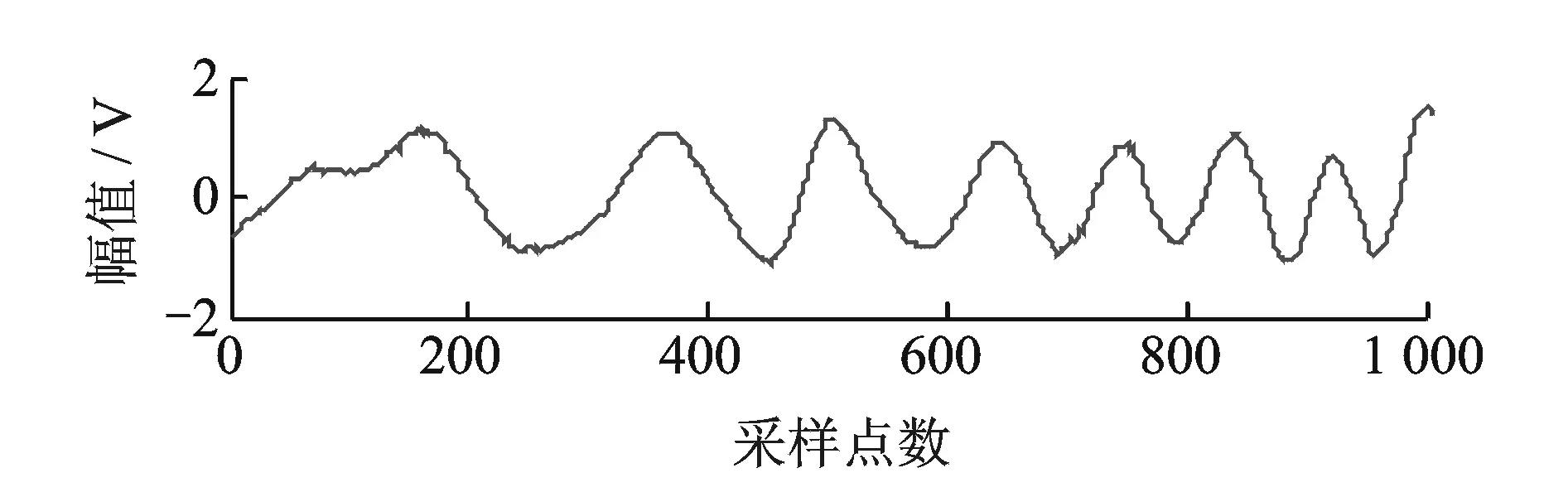
图8 去除工频后的变频信号Fig.8 Frequency modulation signal with 50Hzremoved

3 工程应用分析

为验证所提出的振动信号降噪方法在工程应用上的可行性，将其用于实际转子振动信号的分析，信号采集自新研制的轴承-转子试验台，如图9所示。该试验台可进行阻尼轴承、圆柱瓦轴承等多种类型轴承试验。转子轴颈处安装高精度的电涡流位移传感器测量转子振动，传感器型号为Kaman KD2306S。

图9 轴承-转子试验台Fig.9 Bearing-rotor test bench

在某次试验中，当转子转速为3 840 r/min(64 Hz)时，由LMS数据采集系统以1 024 Hz采样率采集长度为1 024的信号，信号波形如图10所示，频谱如图11所示。由图11可见，振动信号中存在工频干扰。经研究发现，信号中的工频干扰来自于为电涡流位移传感器供电的直流稳压电源。

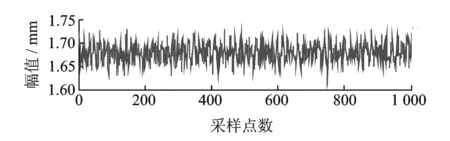
图10 振动信号波形Fig.10 Waveform of vibration signal

将振动信号构造为512×513维Hankel矩阵并作奇异值分解，生成的奇异值谱如图12所示。因直流分量对应的奇异值较大，为方便显示暂将其略去，只显示其余奇异值中的前30个。同理，图13的奇异值差分谱中第1个值也未显示。

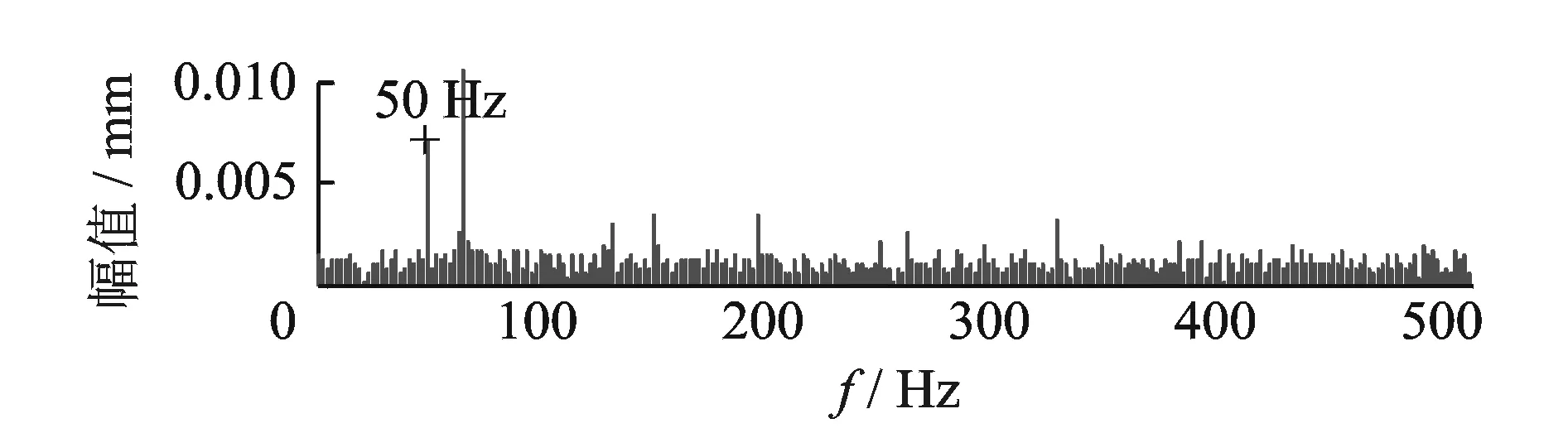
图11 振动信号频谱Fig.11 Spectrum of vibration signal

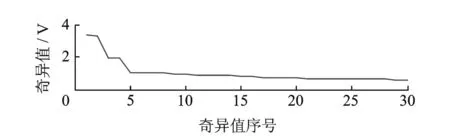
图12 振动信号奇异值谱Fig.12 Singular values spectrum of vibration signal

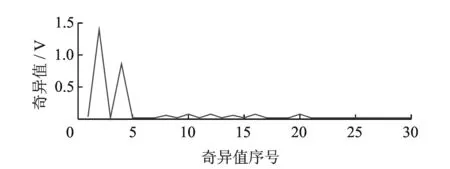
图13 振动信号奇异值差分谱Fig.13 Difference spectrum singular values

图13中从右往左的第1个极大值所在位置为20，因此确定有效奇异值阶次为21，由此有效奇异值阶次重构信号，重构信号波形如图14所示。比较图14和图10可以发现，随机噪声得以明显降低。

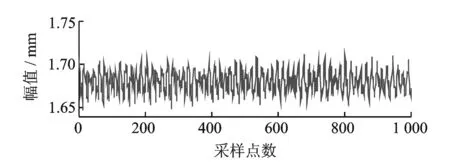
图14 重构信号波形Fig.14 Waveform of reconstructed signal

对左奇异向量u1～u21作FFT，图15给出了前6个幅值谱及u12和u13的幅值谱。图15中，u1的频率为零，代表直流分量；u2和u3的频谱为64 Hz，代表转子基频分量；u4和u5的频谱为50 Hz，代表工频分量；u12和u13的频谱为150 Hz，代表3倍工频分量；u6及其他各奇异向量代表转子其他分量。

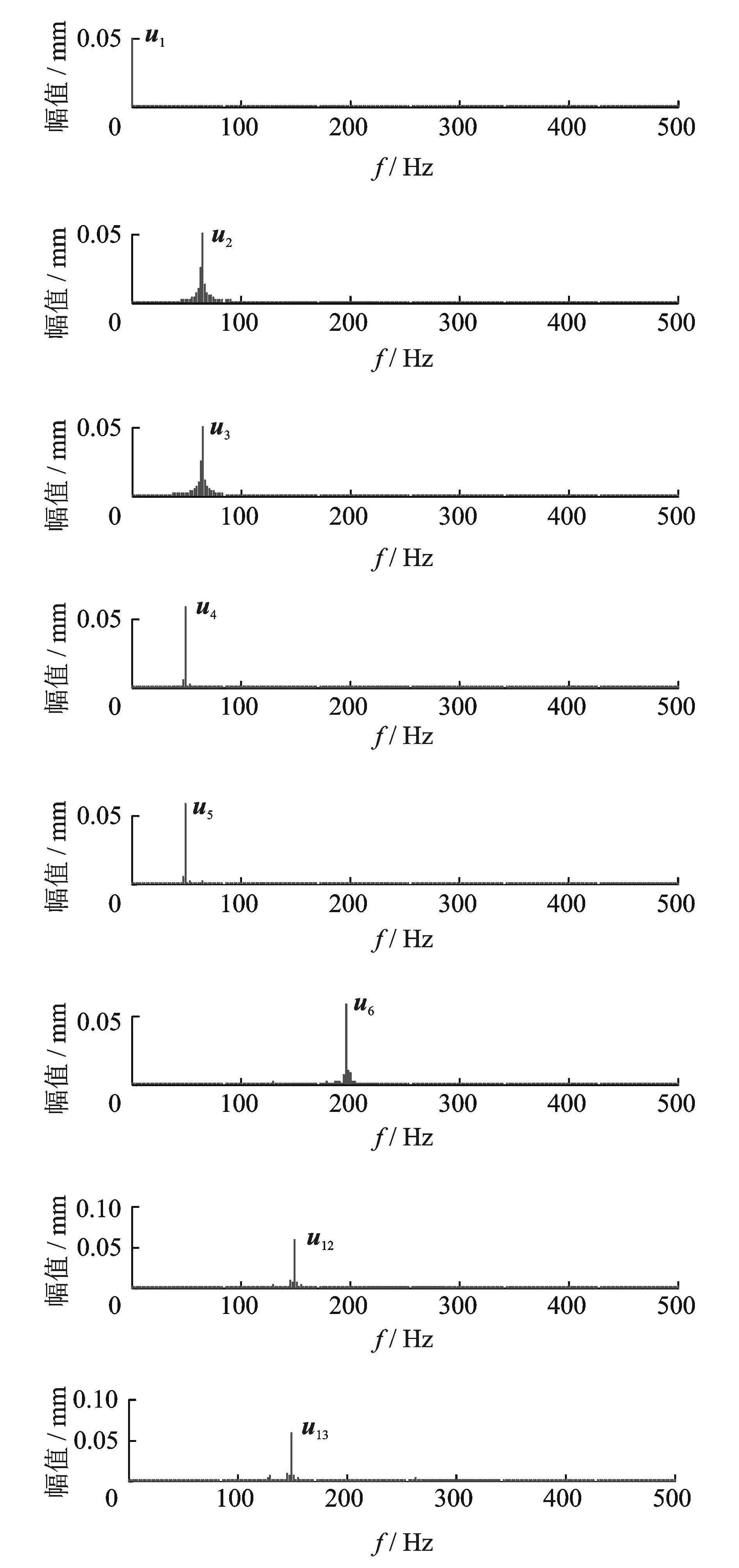
图15 部分左奇异向量频谱Fig.15 Spectrum of part left singular vectors

将第4，5，12，13个奇异值置零，并重构为时域信号，重构信号的波形如图16所示，频谱如图17所示。比较图16和图10、图17和图11可以发现，不但随机噪声被降低，工频噪声也被降低，得到较为理想的转子基频及其倍频信号，从而有利于后续对转子运行状态的分析和诊断。

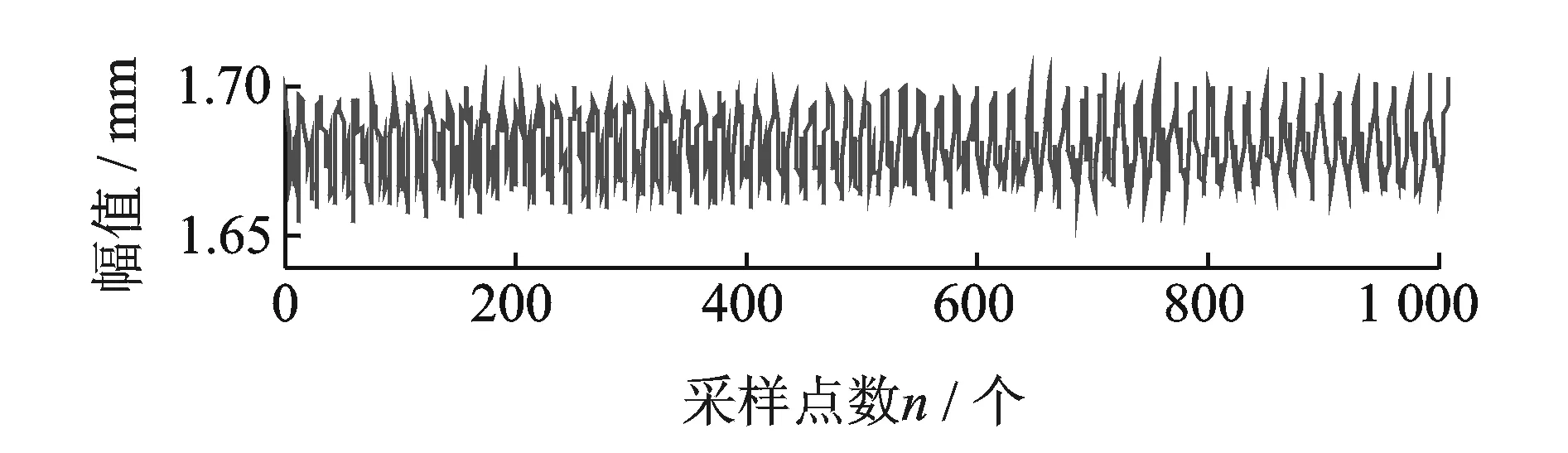
图16 降噪后的信号波形Fig.16 Signalwaveformafter noise deduction

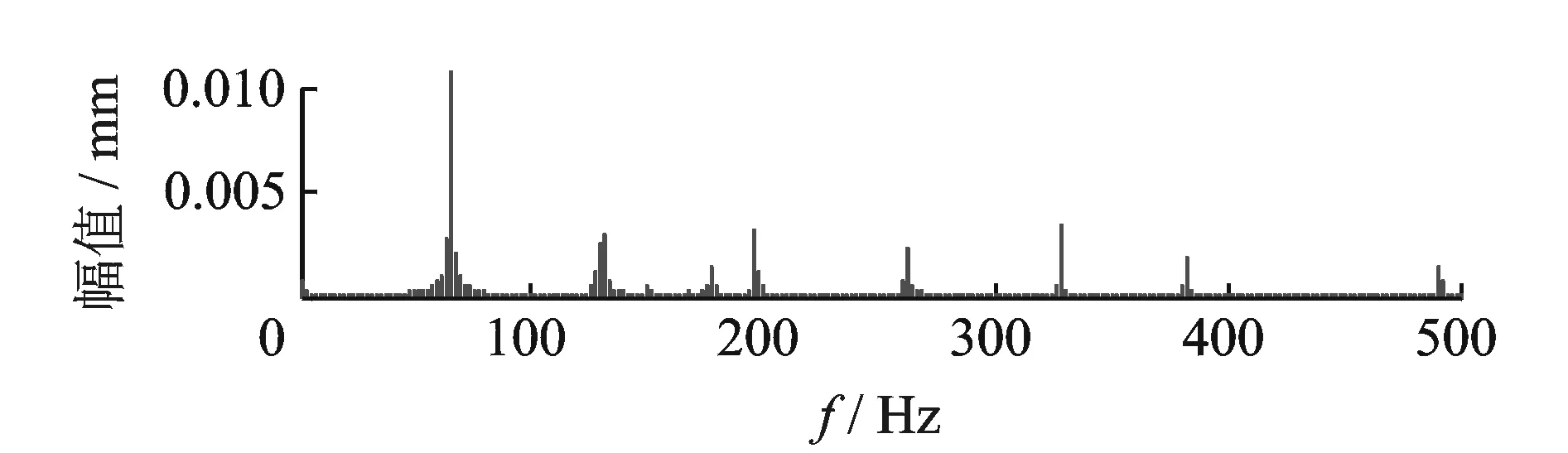
图17 降噪后的信号频谱Fig.17 Signal spectrumafter noise deduction

4 与陷波器滤波结果的对比

由数字滤波器理论[14]可设计出50 Hz工频陷波器，其表达式为

(5)

其中：ω0=2πf0/fs=0.306 8；f0=50 Hz；fs为采样率。

由α值可确定陷波器的深度和宽度，其值越大则凹陷越深、宽度越窄。为得到最佳滤波效果，取该值为0.99。同样可设计150 Hz陷波器。

图10所示工程信号经陷波器滤波后的频谱如图18所示，比较图18和图11可以发现，经陷波器滤波后基频幅值降低，50和150 Hz频谱的邻近有用成分也被滤掉，从而影响后续信号分析和判断。

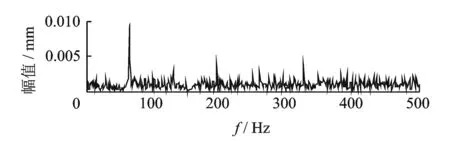
图18 陷波器滤波后的信号频谱Fig.18 Signal spectrum after notch filter processing

5 结束语

针对转子振动信号中的随机噪声干扰和工频干扰共存的问题，提出基于奇异值和奇异向量相结合的振动信号降噪方法。该方法克服了以往奇异值分解方法在降低工频噪声干扰应用中所存在的局限性，不但可以降低随机噪声干扰，而且可以降低工频噪声干扰。通过数值仿真和工程实际信号对所提出方法进行了分析，结果表明该方法是有效的和可行的。

参 考 文 献

[1] Zhao Xuezhi, Ye Bangyan. Singular valued composition packet anditsapplication toextraction of weakfault feature [J]. Mechanical Systems and Signal Processing, 2016, 70/71:73-86.

[2] Reza G, Kenan Y S. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults[J]. Mechanical Systems and Signal Processing,2016,70/71:36-50.

[3] Liu Yuanhong, Yu Zhiwei, Zeng Ming, et al. LLE for submersible plunger pump fault diagnosisvia joint wavelet and SVD approach [J]. Neurocomputing, 2016, 185 (C): 202-211.

[4] 李建,刘红星,屈梁生.探测信号中周期性冲击分量的奇异值分解技术[J]. 振动工程学报,2002,15(4):415-418.

LiJian， Liu Hongxing， Qu Liangsheng. Detection of periodic impulse components in signals using singular value decomposition [J]. Journal of Vibration Engineering， 2002,15(4):415-418.(in Chinese)

[5] 赵学智,叶邦彦,陈统坚.奇异值差分谱理论及其在车床主轴箱故障诊断中的应用[J].机械工程学报,2010,46(1):100-108.

Zhao Xuezhi， Ye Bangyan， Chen Tongjian. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe [J]. Journal of Mechanical Engineering,2010,46(1):100-108. (in Chinese)

[6] 朱启兵,刘杰,李允公.基于结构风险最小化原则的奇异值分解降噪研究[J].振动工程学报,2005,18(2):204-207．

Zhu Qibing, Liu Jie, Li Yungong, et al. Study on noise reduction in singular value decomposition based on structural risk minimization [J].Journal of Vibration Engineering, 2005,18(2):204-207．(in Chinese)

[7] 王维,张英堂,徐章遂.基于动态聚类的奇异值分解降噪方法研究[J].振动工程学报,2008,18(2):304-308．

Wang Wei, Zhang Yingtang, Xu Zhangsui. Noise reduction in singular value decomposition based on dynamic clustering [J]. Journal of Vibration Engineering, 2008,18(2):304-308．(in Chinese)

[8] 张克南,陆扬,谢里阳,等.基于SVD方法的弱故障特征提取方法[J].机床与液压,2006(10):1-5.

Zhang Kenan, Lu Yang, Xie Liyang, et al. A new method for extracting the weak fault symptoms of current signal via SVD [J]. Machine Tool & Hydraulics,2006(10):1-5. (in Chinese)

[9] 吴浩浩,罗志增.基于构造Hankel 矩阵的SVD陷波方法[J].计算机应用研究, 2010,27(12):4514-4517.

Wu Haohao, Luo Zhizeng. Signal notch method based on Hankel matrix and SVD [J]. Application Research of Computers, 2010,27(12):4514-4517. (in Chinese)

[10] 翟亚宁,杨兆建.基于小波包能量谱和BP神经网络的转子系统扭矩激励识别[J].中国农机化学报,2015,36(3): 194-198.

Zhai Yaning, Yang Zhaojian. Torque incentive identification of the rotor system based on wavelet packet energy spectrum and BP neural network[J].Journal of Chinese Agricultural Mechanization,2015,36(3):194-198. (in Chinese)

[11] 梁霖,徐光华,侯成刚.基于奇异值分解的连续小波消噪方法[J]. 西安交通大学学报,2004,38(9):904-908.

Liang Lin, Xu Guanghua， Hou Chenggang. Continuous wavelet transform denoising method based on singular value decomposition [J]. Journal of Xi′an Jiaotong University, 2004,38(9):904-908. (in Chinese)

[12] Groutage D, Bennink D. Feature sets for nonstationary signals derived from moments of the singular value decomposition of Cohen-posch (positive time-frequency) distributions [J]. IEEE Transactions on Signal Processing, 2000,48(5):1216-1223.

[13] 何正嘉,訾艳阳,孟庆丰,等.机械设备非平稳信号的故障诊断原理及应用[M].北京:高等教育出版社,2001:1-2.

[14] 王立会,潘冬明.一种消除心电信号中工频干扰的陷波器设计[J].医疗设备信息,2007,22(7):18-20.

Wang Lihui, Pan Dongming. Design of digital trap for eliminating power-line interference on ECG signals [J]. Information of Medical Equipment, 2007, 22(7):18-20. (in Chinese)