基于监测数据的隔震结构模态参数异变分析*

杜永峰， 祝青鑫， 李万润， 朱前坤

(1.兰州理工大学防震减灾研究所 兰州，730050) (2.西部土木工程防灾减灾教育部工程研究中心 兰州，730050)

引 言

基础隔震技术是通过在上部结构和基础之间设置水平刚度明显小于上部结构抗侧刚度的柔性隔震层来耗散输入上部结构的能量，最终达到减小上部结构地震响应的目的[1]。国内外使用叠层橡胶支座的隔震房屋，经历多次地震考验，效果良好[2]。由于隔震层的水平刚度远小于上部结构，其性能的改变将影响整个结构的响应。为此，文献[3-4]对橡胶隔震支座的性能进行了系统的试验及理论研究，分析了压应力、频率及温度等因素对支座性能的影响，并给出相关变化规律的拟合公式;但这些数据主要是基于实验室数据进行的分析，实际结构所处环境较为复杂，对于隔震结构在实际环境因素作用下的响应实测数据相对较少。结构健康监测即利用现场无损传感技术与结构系统特征分析方法对工程结构实施损伤定位和识别，探测结构的变化[5]。随着健康监测系统的发展，远程、全天候、实时地对结构健康状态进行监控已成为一种发展趋势[6]。文献[7-8]系统阐述了健康监测与损伤诊断的理论与方法，研究了大跨度斜拱桥结构健康监测系统，并为沈阳伯官大桥设计安装了一套完整的结构健康监测系统。文献[9-12]针对超长复杂基础隔震结构的特点，提出隔震结构主要监测内容、健康监测系统的总体设计要求、传感器选型与测点布置原则以及安全评定方法，对某超长复杂隔震结构进行全寿命监测分析，并对隔震结构的时变非线性特性识别进行探索。陈洋洋等[13]为汶川灾后重建的隔震结构设计安装了远程实时监测系统，并给出典型测试记录和初步分析结果。

笔者基于某隔震结构健康监测系统采集的结构在不同工况下的响应数据，采用改进的Morlet小波模态参数识别方法对其进行实时分析处理，识别结构在不同工况下的结构模态参数，分析环境因素以及人为活动对其影响规律，并对监测系统采集到的两次地震响应数据进行分析，给出隔震结构在地震作用下的结构特性变化规律。

1 隔震结构健康监测系统设计与实现

1.1 工程概况

酒钢三中新校区1#教学楼位于甘肃省嘉峪关市，于2015年8月建设完成并投入使用。该建筑总共5层，为钢筋混凝土框架结构，总高度为27.3 m，1层层高为4.5 m，其余层层高为4.2 m，坡屋面拱高为6.0 m。建筑的整体外观如图1所示。为了降低该结构的水平向地震作用，在基础顶部设置叠层橡胶隔震支座，其节点细部如图2所示。

图2 公共教学楼隔震支座节点细部Fig.2 Detailed joint of rubber isolator of public teaching building

为了及时掌握结构运营状况，保证结构安全，为隔震结构的管理与维护决策提供科学依据，并验证与改进隔震结构设计理论与方法，寻找影响隔震结构性能的主要因素，为其设计并安装一套符合该结构特点的长期健康监测系统。

1.2 系统设计与实施

1.2.1 系统总体设计

根据文献[14]中结构健康监测系统等级划分方法，依据该隔震结构的重要性、服役环境等情况，确定该隔震结构健康监测系统为一级，即长期在线实时健康监测系统。同时参考文献[9]提出的基础隔震结构健康监测系统设计方法，基于TeamViewer平台搭建远程实时监测系统平台，实现对该教学楼的远程实时监测。该系统主要架构如图3所示，其主要功能是实时记录并存储环境因素及结构在不同工况下的响应数据，并对其进行实时分析，最终对隔震结构的健康安全状态进行评定和预测。

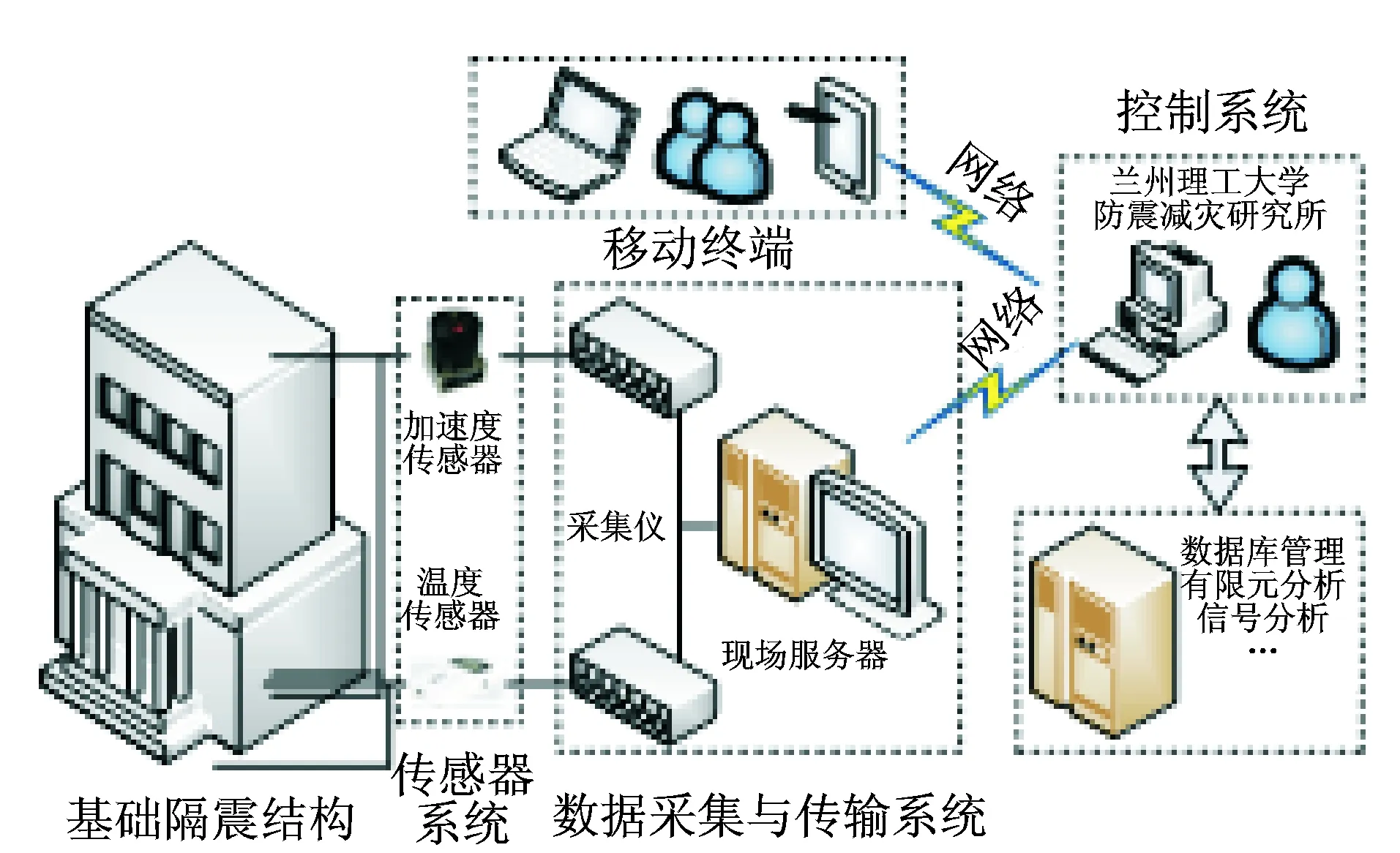
图3 基础隔震结构健康监测系统Fig.3 Base-isolated structure health monitoring system

1.2.2 传感器选择与测点布置

根据该监测系统等级及功能需求，本着技术先进、性能可靠、长期稳定及满足监测要求的目的对设备进行选型。整个系统共采用加速度传感器8个，采集子站1套，主要硬件见表1。

由于隔震层的重要性，在布置传感器时，除了按常规结构健康监测系统进行传感器布置之外，还需在隔震层布置专门的传感器。具体布置位置如图4、图5所示。

表1 监测设备

图4 隔震建筑测点示意图Fig.4 Sketch of measuring points for base-isolated building

图5 加速度传感器Fig.5 Acceleration transducer

温度传感器布设时，由于隔震层不同位置所采取的构造措施不同，并且隔震层也常常分布各种管道，尤其是暖气管道的存在会严重影响隔震层的温度分布，因此主要采用温度传感器对隔震层温差较大位置进行监测，例如隔震层与室外交界处、暖气管道附近等，从而得到隔震层温度场的变化。上部结构由于存在各种保温措施，通过现场测定，温度较为恒定，因此未对上部结构布置温度传感器。

在考察隔震结构动力响应时，主要采用加速度传感器。分别在隔震结构基础、隔震层顶板的三个方向及顶层楼板的两个水平方向布设加速度传感器，考察该结构在环境激励及地震作用下结构振动响应通过隔震层前后的变化以及隔震结构整体的响应，为后续状态评估和研究工作做好准备。

各传感器按照系统时间进行同步采集，温度传感器采样时间间隔设定为15 min，加速度传感器采样频率设定为100 Hz，数据由采集子站(图6)进行储存和管理。为了保证断电状态系统仍能进行数据采集和存储，采集子站配置了不间断电源。服务器接入互联网，基于TeamViewer软件建立远程实时监测平台，可以通过远程登录实现对系统的远程操作，对数据可直接进行分析处理或下载操作。

图6 现场长期采集站Fig.6 Located long-time acquisition station

2 改进的Morlet小波模态参数识别原理

采用改进的Morlet小波，可以提高频域分辨率，在满足Heisenberg测不准原理的前提下可以协调频域和时域分辨率达到最佳折衷状态[15-16]。

(1)

其中：fb为带宽参数；fc为小波中心频率。

线性多自由度系统自由振动响应的解析形式为

(2)

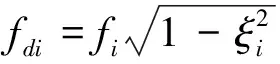
改进的Morlet小波变换[16]可以表示为

(3)

对于多自由度系统，尺度参数为ai的小波变换系数可写成

(4)

引入一个随时间变换的振幅Bi(t)和相位φi(t)可将上式转化成

(5)

当ai=fc/fi时，小波变换系数对应点(a,t)平面的位置成为小波脊在此脊线上小波系数的模|WTx(a,t)|的对数的斜率，即为-2πξifi；小波系数的相位的斜率即为系统的固有频率

(6)

(7)

由式(6)和式(7)即可推导出体系的固有频率和阻尼比

采用上述改进的Morlet小波模态参数识别算法，基于Matlab数值分析软件进行编程，对长期健康监测系统实时采集数据进行分析处理。

3 环境激励下监测数据分析

环境激励下影响隔震结构性能的因素较多，由于该结构的使用特点及所处地理位置，主要考虑人员活动及温度变化的影响。单日监测数据分析时，上部结构人员集中变化现象比较明显；长期监测数据分析时，该结构地处寒冷地区，冬夏最大温差可达60℃，温度变化对隔震支座性能变化影响较为明显。该隔震结构单日上部质量变化及长期隔震层性能变化如图7所示。

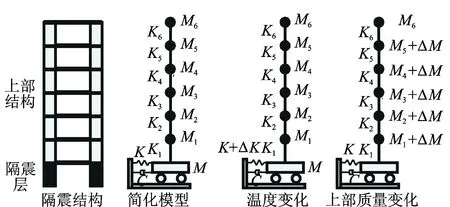
图7 结构简化模型Fig.7 Simplified models of base-isolated structure

3.1 单日数据变化分析

3.1.1 单日数据变化影响因素分析

该隔震结构的使用功能为教学楼，活荷载主要为学生质量及其携带的日常用品。根据该结构使用功能，存在典型3种使用状态，即空载状态、课间活动状态及正常上课状态。给出2016年6月14日及15日两天该隔震结构质量变化及隔震层中部温度变化规律。根据图8分析可知，单日隔震层温度变化不明显，故单日数据变化分析时不计温度变化的影响。

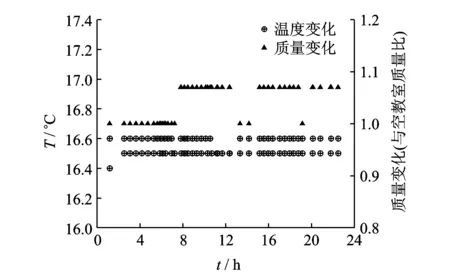
图8 不同影响因素变化分析Fig.8 Change analysis of different influencing factors

3.1.2 单日数据时域变化分析

分别选取不同状态下隔震结构顶层屋面短向加速度时程数据各600 s，给出其时域对比图,如图9所示。

图9 不同状态加速度时程图Fig.9 Acceleration time histories of different states

由图9可知，不同状态下加速度响应变化较大。选取2016年6月14日及15日两天隔震结构顶层短向加速度数据，按该校作息时间表对不同状态下的响应数据进行分段截取，对各段加速度数据有效值进行统计分析，如图10所示。

由图10可以看出，空教室状态下，夜间结构加速度响应较小；白天环境激励增多，结构响应有所增大。正常上课状态下，结构响应增大较多；课间活动状态下，结构加速度响应明显增大，说明人员活动对结构加速度响应影响十分显著。该指标可作为评判该隔震结构工作状态的标准。

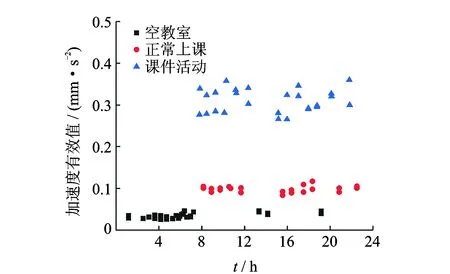
图10 加速度有效值Fig.10 Acceleration effective value

3.1.3 单日数据模态变化分析

上部结构质量的变化将直接影响结构模态参数的变化，采用小波变换方法分别对3种状态下的各600s加速度响应数据进行时频分析，如图11所示。

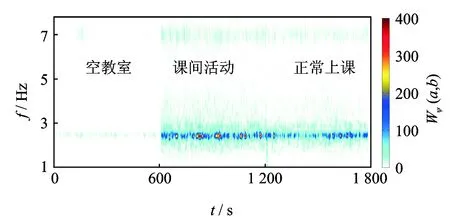
图11 加速度响应时频分析Fig.11 Time-frequency analysis of acceleration response

由图11可以看出，相对于空教室状态，正常上课状态及课间活动状态的模态频率有所减小，频率成分更加丰富。对上述选取的两天的加速度响应分段数据，采用改进后的Morlet小波识别算法对模态参数进行识别，给出其各个时段的阻尼比及频率变化，如图12、图13所示。

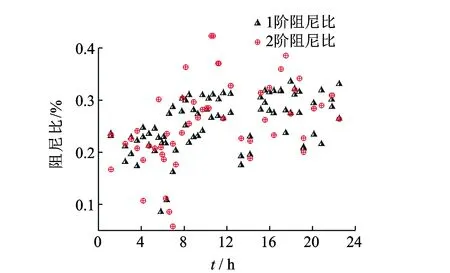
图12 1天内阻尼比变化Fig.12 Variation of damping ratio in one day time

图13 1天内频率变化Fig.13 Variation of frequency in one day time

由图12可以看出，上部人员集中时，结构阻尼比明显增加，这是因为考虑人与结构的耦合作用会增加系统阻尼比，人员处于不同状态时的影响也不同，行走时影响较大，并且行走步频也有很大影响[18]，这有利于结构耗散外部能量的输入。由图13可以看出，人员集中时，结构频率降低。上部质量变化与前2阶模态频率与阻尼的相关性系数分别为-0.560 6，-0.512 9，0.735 5和0.744 3，隔震结构单日模态参数变化受上部人员活动影响较大。

3.1.4 上部人员活动对隔震性能的影响

上部结构活荷载主要为学生及所携带学习用品，质量变化较大。考虑上部活荷载作用下的不同情况，采用有限元软件对该隔震结构不同使用状态下的隔震性能进行分析。质量变化数据主要根据设计院所出具的设计报告以及现场考察结果。采用实测地震数据进行调幅后作为输入激励，不同状态下层剪力比(结构隔震后层间剪力与隔震前层间剪力的比值)、周期比(结构隔震后1阶周期与隔震前1阶周期的比值)及隔震层位移如图14及表2所示。

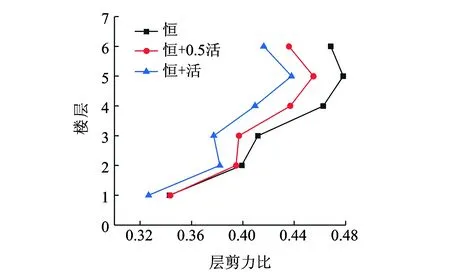
图14 层剪力比随荷载组合的变化Fig.14 Variation of layer shear force ratio with loading combinations

由图14和表2可以看出，上部人员变动对隔震结构性能影响较为明显，后续对人员集中变动比较明显的结构(如教学楼)进行设计时，建议对不同状态下分别进行分析验算。

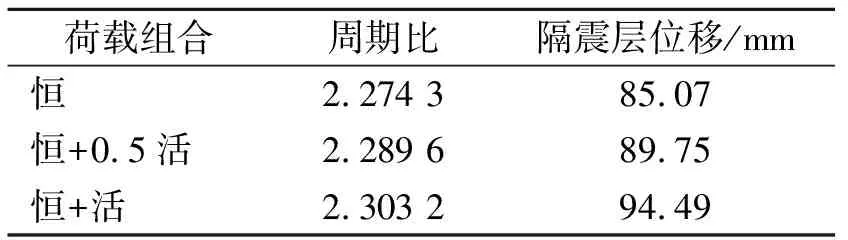
表2 隔震结构性能参数随荷载组合变化表

3.2 长期数据变化分析

3.2.1 长期数据变化影响因素分析

该结构位于我国西北部，温差较大，根据文献[3-4]，温度变化对隔震支座性能影响较大。温度变化也会影响上部结构的材料力学性能，并且会影响结构的几何特性，改变结构的内力状态，使结构的模态参数产生改变。

现给出从2016年3月12日至2016年6月19日共100天温度变化数据。由实测数据可知，靠近隔震沟和隔震缝附近与外界温度热交换比较直接，温差变换较大，位于隔震层中心处温度变化比较缓慢。实测温度数据变化如图15所示。

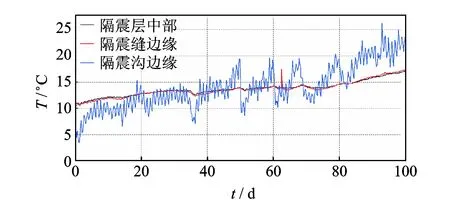
图15 温度变化Fig.15 Change of temperature

隔震层不同位置处温度变化幅度大有不同，经长期数据统计分析，其变化存在联系，如图16所示。下面的分析均以隔震层中部温度变化为主要因素进行分析。

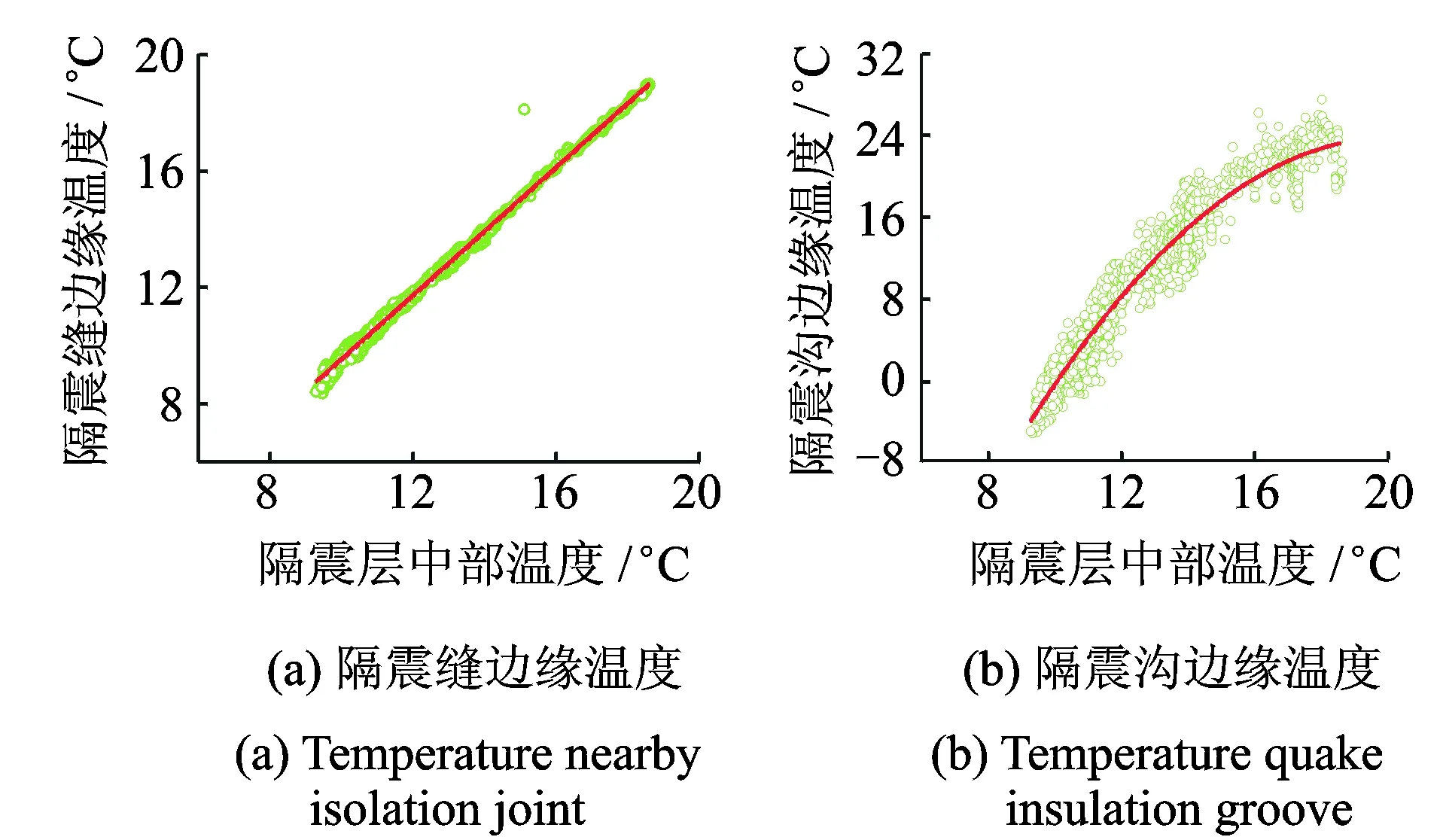
图16 不同位置处温度变化关系Fig.16 Changing relation between different location temperature

3.2.2 长期数据模态变化分析

为忽略上部人员集中质量变化影响，截取2016年3月12日至2016年6月19日中每日凌晨时1 200 s顶层屋面加速度响应数据，采用改进Morlet小波识别算法进行分析，给出结构阻尼比及频率变化规律，如图17、图18所示。

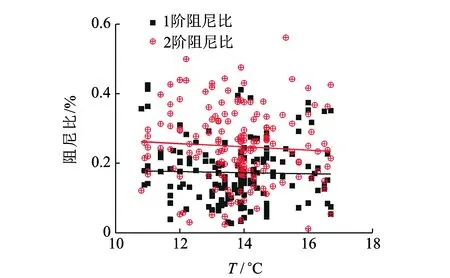
图17 阻尼比随温度的变化Fig.17 Variation of damping ratio with temperature

图18 频率随温度的变化Fig.18 Variation of frequency with temperature

由图17可以看出，1阶阻尼比在0.16%附近变动，2阶阻尼比在0.26%附近变动，均低于设计值。随着温度升高，结构阻尼比有所降低，但变化幅度十分缓慢。由图18可以看出，1阶频率在2.45 Hz附近变动，2阶频率在7.0 Hz附近变动，均高于设计值。模态频率随着温度的升高而降低，并且在低温时温度变化对其影响更加明显。温度变化与前2阶模态频率与阻尼的相关性系数分别为-0.508 7，-0.507 5，-0.125 8和-0.163 5，隔震结构长期模态参数变化受温度变化较大。

3.2.3 温度变化对隔震性能的影响

隔震层性能会受温度荷载的影响，并将影响整个结构的响应。采用有限元软件对该隔震结构不同温度状态下的隔震性能进行分析。根据隔震层温度场的实测结果，并参考文献[3-4]，对不同温度下支座性能进行修正。采用实测地震数据进行调幅后作为输入激励，不同状态下层剪力比(结构隔震后层间剪力与隔震前层间剪力的比值)、周期比(结构隔震后1阶周期与隔震前1阶周期的比值)及隔震层位移如图19及表3所示。

图19 层剪力比随温度的变化Fig.19 Variation of layer shear force ratio with temperature

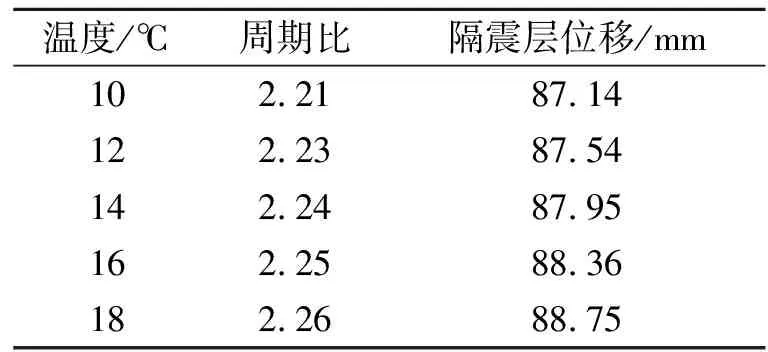
表3 隔震结构性能参数随温度变化表

由图19和表3可以看出，温度变化对隔震结构性能影响较为明显，因此，在低温地区进行隔震设计时应充分考虑温度变化对隔震层性能的影响，对隔震层采取相应的保温措施。

4 地震激励下监测数据分析

该隔震结构健康监测系统于2015年8月正式投入使用，至今已成功监测该隔震结构在地震作用下的响应两次，两次地震基本信息如表4所示。

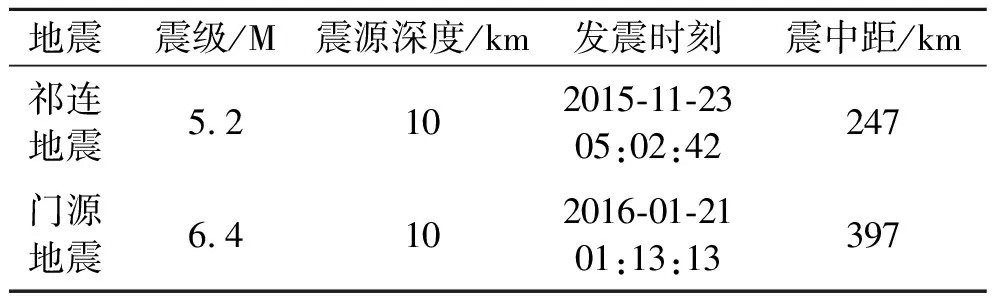
表4 地震基本信息

4.1 地震激励下时域响应分析

根据监测系统记录隔震结构在两次地震作用下基础、隔震层顶板及顶层屋面加速度响应数据。给出加速度时程图如图20所示。

图20 加速度时程曲线Fig.20 Acceleration time histories

由图20可知，两次地震作用下基础加速度峰值分别为0.27和0.41gal，顶层屋面加速度峰值分别为0.99和2.31gal。相对于基础，顶层加速度分别放大了3.7倍和5.6倍，这是由于地震加速度峰值很小时，隔震结构的位移响应无法达到预期的设计位移，结构的有效周期无法延长至设计周期，因此隔震效果不明显，隔震层未能完全发挥作用，但这有利于隔震结构的抗风设计。

4.2 地震作用下频域变化分析

采用改进后的Morlet小波算法对采集到的两次地震作用下的顶层屋面加速度响应做时频分析，如图21所示。由图21可以看出，相对于环境激励下，地震作用下结构振动频率变低，频率成分更加丰富。随着振幅增大，自振频率降低更加明显。取地震时150 s及地震前后环境激励下各100 s屋面顶层短向加速度响应数据，以每50 s数据为一段对其频率及阻尼比进行识别分析，得到结构频率及阻尼比变化如图22、图23所示。

图21 地震响应时频分析Fig.21 Time-frequency analysis of seismic response

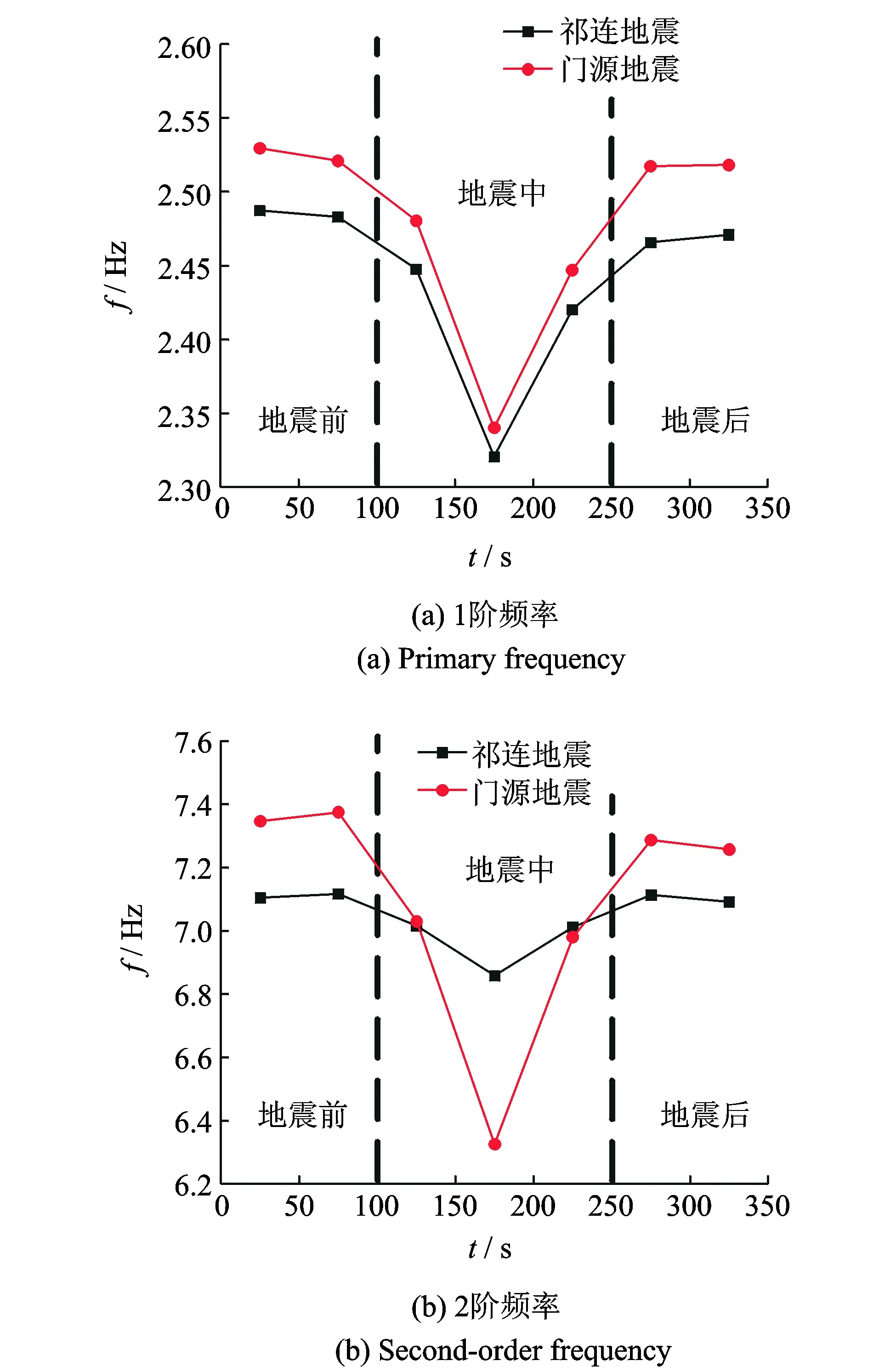
图22 频率变化分析Fig.22 Change analysis of frequency

图23 阻尼比变化分析Fig.23 Change analysis of damping ratio

由图22、图23可以看出，小震激励下，随着地震激励幅值的增加，结构自振频率减小，阻尼比增加，直到地震加速度幅值达到最大。随后，地震加速度幅值开始减小，结构自振频率增大，阻尼比减小。从两次地震激励下结构响应可知，地震激励加速度幅值越大，频率及阻尼比变化越大。但由于两次地震激励均较小，隔震层未能有效发挥作用，频率及阻尼比均未能达到设计值。

隔震结构的振动特性强烈依赖于震动强度。导致这种现象的原因有：a.隔震支座进行加载实验结果[3-4]表明，当隔震支座由静止状态开始进行实验加载时，初始为一斜率渐变的曲线，即隔震支座的初始刚度并非像理论中线性化的常数刚度；b.房屋结构中存在大量的非结构构件(填充墙、粉刷装饰及管道等)，它们不参与整体承载，但在小幅反应时提供的刚度远大于结构承载体系本身的刚度[19]，并且随着振动幅值的增加与减小，部分附属结构与主体结构会出现“松动”和“连接”现象，导致上部结构刚度与阻尼的增加与减小；c.能量耗散因素(如结构材料的内摩擦、各构件连接处的摩擦以及周围介质的阻力等)受结构振动幅值影响，建筑结构在环境激励及较小地震激励下，结构振动幅值较小，结构原有耗能机制未能有效发挥作用，随着激励幅值的增加，结构耗能机制逐渐发挥作用，结构阻尼比随振动强度的大小而改变。

5 结 论

1) 单日监测数据分析表明，人员活动是影响隔震结构的主要因素，对结构响应、模态频率及阻尼比变化有较大影响。

2) 长期监测数据分析表明，温度是影响结构模态参数的主要因素。结构频率随温度升高而降低，尤其在温度较低时，温度变化对结构自振频率影响较大。随着温度的增加，结构阻尼比有所减小，但其变化较为缓慢。

3) 地震输入加速度幅值较小时，隔震层未能完全发挥作用，隔震效果不明显。但随着激励幅值增加，频率降低，阻尼比增大，隔震结构的振动特性强烈依赖于地震动强度。

参 考 文 献

[1] 王亚楠, 李慧, 杜永峰. TMD-基础隔震混合控制体系在近场地震作用下的能量响应与减震效果分析[J]. 振动与冲击, 2014, 33(4):204-209.

Wang Yanan, Li Hui, Du Yongfeng. Energy response and anti-vibration effect analysis for a base-isolated structure with TMD under near-field earthquake[J]. Journal of Vibration and Shock, 2014, 33(4): 204-209. (in Chinese)

[2] Hijikata K,Takahashi M,Aoyagi T, et al. The behavior of base-isolated building at fukushima dai-ichi nuclear power plant during the great east Japan earthquake[C]∥ Proceedings of the International Symposium on Engineering Lessons Learned from the 2011 Great East Japan Earthquake. Tokyo, Japan:[s.n.] ,2012:1542-1551.

[3] 刘文光, 李峥嵘, 周福霖,等. 低硬度橡胶隔震支座基本力学性能及恢复力特性[J]. 地震工程与工程振动, 2002, 22(3):138-144.

Liu Wenguang, Li Zhengrong, Zhou Fulin, et al. Force-displacement relation and fundamental properties of low stiffness rubber bearings[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(3):138-144. (in Chinese)

[4] 沈朝勇, 谭平, 崔杰,等. 超低硬度橡胶隔震支座水平力学性能相关性试验研究[J]. 地震工程与工程振动, 2014, 1(5):204-216.

Shen Chaoyong, Tan Ping, Cui Jie, et al. Experimental study on dependence of horizontal mechanical property of elastomeric isolators with ultra-low hardness[J]. Earthquake Engineering and Engineering Vibration, 2014, 1(5):204-216. (in Chinese)

[5] Housner G W, Bergman L A, Caughey T K, et al. Structure control: past, present and future[J]. Journal of Engineering Mechanics, 1997, 123(9): 897-971.

[6] Auweraer H V D, Peeters B. International research projects on structural health monitoring: an overview[J]. Structural Health Monitoring, 2003, 2(4):341-358.

[7] Li Hongnan, Li Dongsheng, Song Gangbing. Recent applications of fiber optic sensors to health monitoring in civil engineering[J]. Engineering Structures, 2008, 26(11):1647-1657.

[8] 李宏男, 田亮, 伊廷华,等. 大跨斜拱桥结构健康监测系统的设计与开发[J]. 振动工程学报, 2015(4):574-584.

Li Hongnan, Tian Liang, Yi Tinghua, et al. Design and development of structural health monitoring system for long span skew arch bridge[J]. Journal of Vibration Engineering, 2015(4):574-584. (in Chinese)

[9] 李万润, 郑文智, 杜永峰,等. 基础隔震结构健康监测系统的设计与实现(I):系统设计[J]. 地震工程学报, 2016, 38(1):94-102.

Li Wanrun, Zheng Wenzhi, Du Yongfeng, et al. Design and implementation of structural health monitoring system for base-isolated structure (I):system design[J]. China Earthquake Engineering Journal, 2016, 38(1):94-102. (in Chinese)

[10] 杜永峰, 郑文智, 李万润,等. 基础隔震结构健康监测系统的设计与实现(II):系统实现[J]. 地震工程学报, 2016, 38(3):344-352.

Du Yongfeng, Zheng Wenzhi, Li Wanrun, et al. Design and implementation of health monitoring system for base-isolated structure (II):system implementation [J]. China Earthquake Engineering Journal, 2016, 38(3):344-352. (in Chinese)

[11] 杜永峰, 赵丽洁, 张韬,等. 超长复杂隔震结构施工力学及全过程监测研究[J]. 工程力学, 2015, 32(7):1-10.

Du Yongfeng, Zhao Lijie, Zhang Tao, et al. Study on construction mechanics of long complicated isolated structures and life-cycle monitoring[J]. Engineering Mechanics, 2015, 32(7):1-10. (in Chinese)

[12] 杜永峰, 赵丽洁, 李万润,等. 基础隔震结构橡胶支座时变非线性特性识别[J]. 振动、测试与诊断, 2016,36(1):86-91.

Du Yongfeng, Zhao Lijie, Li Wanrun, et al. Identification for time-varying nonlinear properties of rubber-bearings in base-isolated buildings[J]. Journal of Vibration, Measurement & Diagnosis, 2016,36(1):86-91. (in Chinese)

[13] 陈洋洋, 谭平, 陈建秋,等. 汶川灾后重建的隔震建筑远程实时监测[J]. 中山大学学报:自然科学版, 2013, 52(4):76-82.

Chen Yangyang, Tan Ping, Chen Jianqiu, et al. Remote real-time monitoring for seismic isolated buildings in the Wenchuan post-disaster reconstruction[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni:Natural Science Edition, 2013, 52(4):76-82. (in Chinese)

[14] 李惠, 欧进萍. 斜拉桥结构健康监测系统的设计与实现(Ⅰ):系统设计[J]. 土木工程学报, 2006, 39(4):39-44.

Li Hui, Ou Jinping. Design and implementation of health monitoring systems for cable-stayed bridges (I):design methods[J]. China Civil Engineering Journal, 2006, 39(4):39-44. (in Chinese)

[15] 杨福生. 小波变换的工程分析与应用[M]. 北京：科学出版社, 1999:1-5.

[16] 罗光坤. Morlet小波变换理论与应用研究及软件实现[D]. 南京：南京航空航天大学, 2007.

[17] 赵丽洁. 基于小波变换的结构模态参数识别研究[D]. 兰州：兰州理工大学, 2013.

[18] Salyards K A, Hua Y. Assessment of dynamic properties of a crowd model for human-structure interaction modeling[J]. Engineering Structures, 2015, 89:103-110.

[19] 秦权. 桥梁结构的健康监测[J]. 中国公路学报, 2000, 13(2):37-42.

Qin Quan, Health monitoring of long-span bridges[J]. China Journal of Highway and Transport, 2000, 13(2):37-42. (in Chinese)