液压机校平铝板过程中挠变形计算的探讨
2020-06-03王涛
王涛
(大连汇程铝业有限公司,辽宁 大连116105)
1 概述
在汽车、交通运输等行业,随着轻量、节能概念的需求,汽车和其他交通运输工具的制造材料开始大量采用铝及铝合金材料。在铝和铝合金材料中,铝板由于其重量轻、强度高、韧性好等特点,在汽车和交通运输工具的制造中应用量越来越大。但是在这些铝板的新增需求中,对铝板的平度要求却越来越严格。目前,铝板的平度交货标准,已经从单纯的满足欧洲标准和美国标准的平度公差要求,逐步向满足欧洲和美国标准平度公差要求的3/4~1/2 范围过渡。除此之外,用户还会根据自身需要,增加短跨距的平度检测要求。
一直以来,铝板平度公差,都是通过传统的辊式矫直和拉伸矫直来进行。辊式矫直是通过让铝板在辊间反复变形,并利用铝板的反向残余变形来消除铝板的不平度。拉伸矫直则是采用在铝板两端向外拉拽,将铝板抻平的方式。这两类矫直方式在校平过程中都难以对平直进行高精度控制,并且二者更加注重整板的平直度,而对局部的凸起和凹陷的不平度矫正效果不好。往往矫正后的板材,虽然整板能够满足标准要求的平度,但是在短跨距平度检测时,很难通过检测。因此,一些铝板的生产厂家开始采用压力机局部压平的工艺对铝板的平度进行局部平度矫正。这种方式的目的就是为了对铝板局部不平度进行精确矫正。但在校平的实际生产中发现,校正后铝板的最大变形往往偏离校平施压点一段距离,这对铝板能否准确对缺陷位置校平影响很大。因而,如何精确地确定校平位置是很多工程技术人员的研究重心。本文对铝板压弯过程和实际工况进行分析,通过铝板校平过程中挠变形进行计算,总结和归纳了铝板在校正过程中的挠度的变化规律。
2 挠变形公式的推导过程
一般来说,铝板校平的过程,类似一个两端简支的梁在承受中间集中载荷下铝板弯曲的过程。图1 为铝板在压弯工作时的受力简图。
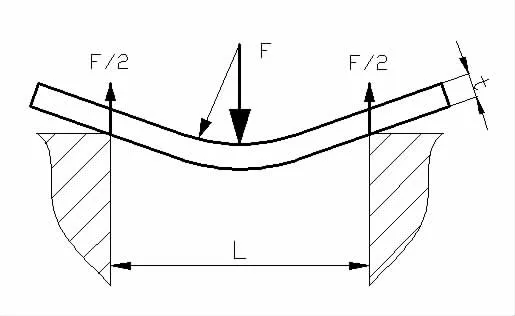
图1 压力校平示意图
首先,铝板被安放在两端的A、B 支点上,铝板上需要校平的点位于两个支点间的悬空位置,在铝板上方施加校平压力。铝板在校平压力的作用下,铝板上需要校平的局部高点被向下压弯,形成向下的挠度,当挠度达到一定程度时,铝板的内应力也将达到材料的屈服极限,铝板开始产生塑性变形。而当校平压力卸载,铝板回弹,但由于铝板塑性变形后产生的残余变形将与铝板的高点偏差相抵消,从而使铝板变得平直。由此可见,铝板校平过程,所以对铝板校平作用力的分析,可以从铝板变形的挠曲线分析入手, 通过挠曲线的近似微分方程的求解和对铝板截面的应力分析,可以获得校平压力与挠度的关系。铝板上需要校正的部位,随机分布,因而铝板的挠曲线应为图2 所示。
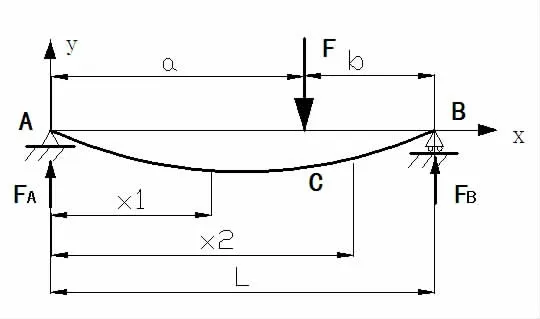
图2 铝板在矫正压力作用下挠度图
铝板可以看做是一个等截面的简支梁,抗弯刚度EI 为常量,受集中校平压力F 的作用。其弯曲变形如下:
由受力的平衡方程,可知A、B 两点的支撑力分别为:
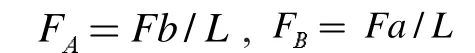
以受力点C 为分界,对铝板截面分AC、CB 两段列弯矩方程,即:
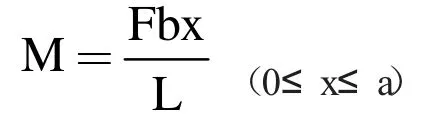
铝板上的弯矩M与铝板的挠度有如下关系,即:
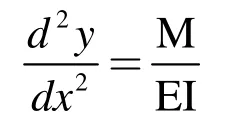
铝板挠曲线上AC、CB 两段的微分方程及其积分,并利用边界条件确定积分常量,可获得以下转角公式和挠变形公式:

在铝板横截面上截面转角θ 近似于挠曲线上一点的切线与x 轴的夹角,故截面转角公式:θ≈dy/dx
当转角θ 为0 时,板片最大挠度将发生在AC 段内,故可得
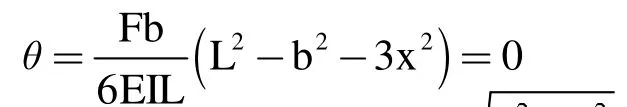
该处为最大挠度位置,可见挠曲线上并不是大多数点的最大挠度出现在板片的正中位置。只有在b=L/2 时,挠度最大值才会在板片的正中位置。
3 挠变形公式的应用
3.1 板片校平位置的确定
在实际生产中可以利用此公式设置校平点位置,例如:校平位置在距板片支撑点x=500mm,支撑跨度L=1500mm,根据公式可以求解施加校平压力的位置距另一侧支撑点的位置,即b 的宽度:
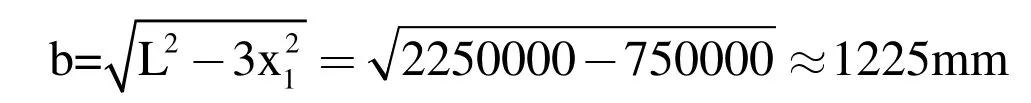
所以,应在距B 端1225mm 处施加校正力,而最大挠变形出现在x=500mm 的位置处。
3.2 板片变形量的确定
在已知校平压力和板片常数的条件下,上述公式还可对板片纠正变形量进行计算。例如:如图2 所示,校正点x 位置在距A 支撑点500mm 处,压力机输出压力F= 1.23×106N,6061 合金铝合金板的弹性模量E=68.9GPa,截面惯性矩I=2.0×10-7m4,铝板厚度h=20mm,校正区域长度B=300mm,支撑跨度L=1500mm,求校正变形量。
由3.1 可知校正力作用点C 的坐标在距B 端1225mm 处,最大变形量为:
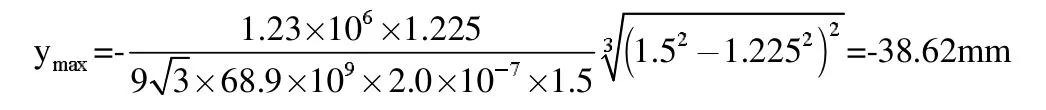
即,x 点处向下的挠变形量最大为38.62mm,此数值与现场实际基本一致。
结束语
综上所述,本文系统介绍了铝板在平度校正过程中的受力分析,并对板片挠曲变形的计算公式进行了推导。根据推导的结论,得出了在压力校正过程中板片挠曲变形的变化规律,以及最大挠变形位置和变形量的确定公式。本文还利用所得公式,结合现场实际,例举了在生产中经常使用的两个应用实例,从而验证了公式的有效性。
