性能台转动惯量在线测量系统及误差分析

杨原青，徐志刚，王军义，王清运

(1.中国科学院 沈阳自动化研究所， 沈阳 110016; 2.东北大学 机械工程与自动化学院， 沈阳 110819； 3.中国科学院大学， 北京 100049)

飞行器的转动惯量等的质量特性的变化，对于其在太空失重环境的运行状态、运动姿态有重要影响，转动惯量的准确测量对于飞行器等设计和控制具有重要的意义[1]。单轴气浮平台是用来模拟竖直方向失重运动的重要设备，同时也能够辅助测量大型飞行器的质量特性参数[2]。本文在有限元仿真软件和现场实验的基础上，研究扭摆法测量物体转动惯量，提出一种等效在线转动惯量测量方法[3]。

1 扭摆法测量转动惯量原理

扭摆法是用于测量大型不规则物体转动惯量的常用方法之一。利用扭摆法所搭建的转台系统基本结构包括：机架、扭杆、轴承和托盘。扭摆法测量原理如图1所示。托盘用来放置待测物品，扭杆通过角接触球轴承固定到机架上，在实验中利用扭杆带动托盘物体做周期性扭转。利用光栅传感器测量托盘的扭转周期，然后将测量数据经过计算机处理，输出被测物体的转动惯量[2]。

图1 扭摆法原理

扭摆法测量转动惯量主要利用扭杆提供周期性回复力使托盘与待测物品周期性振动，测得振动周期。因此在获得准确的转动惯量与扭摆杆的性质密切相关。通过微元法，可以将扭摆杆分解为由无数个二力杆组成。在理想情况下，杆受到扭转力矩使其小角度周期扭转时，变形方向发生在切向，轴向不发生形变。当扭摆杆受到扭转力矩时，分析其轴向的受力及变形。将扭杆看成由无数个理想的拉压二力杆组成，二力杆在受到扭转力矩时在轴向产生拉压应力应变具有非线性变化特性。在圆柱坐标系计算，如图2所示[4]。

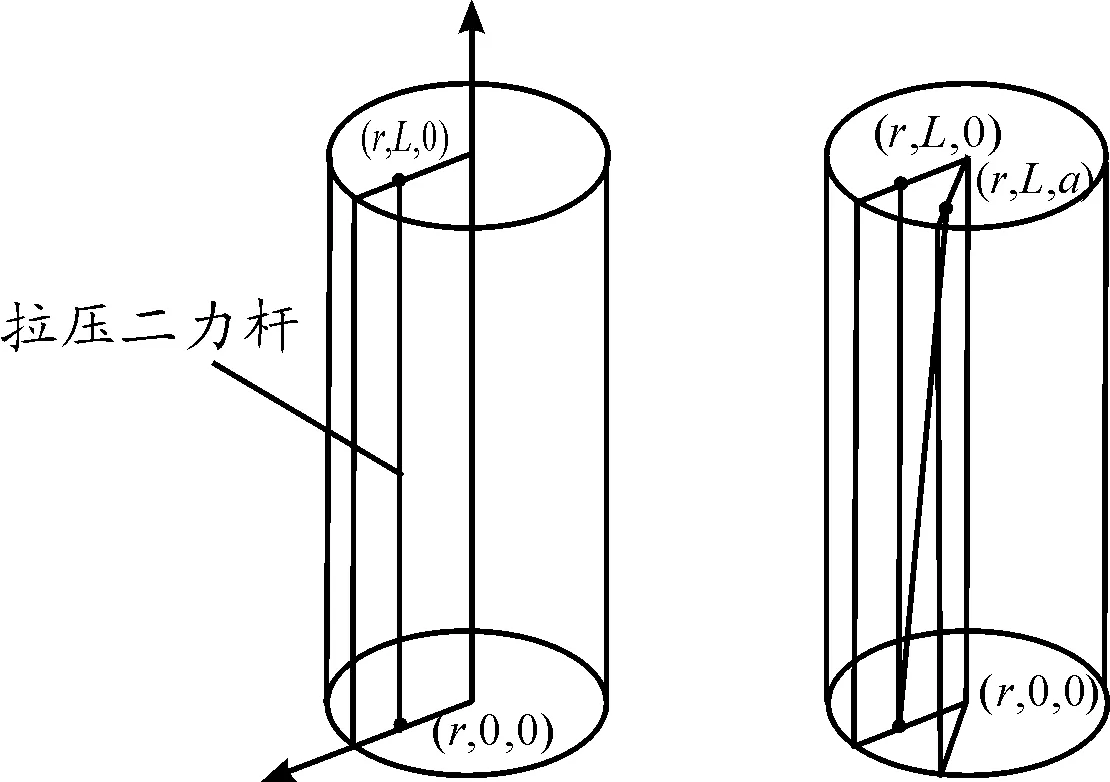
图2 拉压二力杆变形图

二力杆长度变化

(1)

通过ANSYS对3根不同的杆进行受力分析，当杆在受到扭转力矩时，其长径比参数如表1。

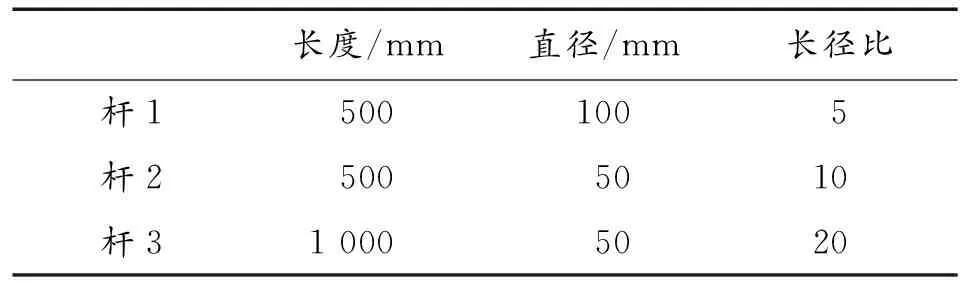
表1 拉杆长径比

通过ANSYS实验仿真分析得出：长径比越大，形变量越大，因此在实验中选择短粗型的扭摆杆。当扭摆杆发生一定角度的扭转时，各个二力杆的内部形变如图3所示。在进行航天飞行器地面仿真时，选择短粗型的扭摆杆，但是采用扭摆法的误差影响仍然较大，故本文提出一种新的方法。

图3 扭摆杆受扭转力矩形变图

2 在线转动惯量测量原理

航天飞行器偏航方向转动的失重运动状态模拟主要采用气浮原理克服摩擦阻力及阻力矩，即在飞行器底部设置气足装置，并将整个飞行器置于光滑平整的花岗岩平台上。充气后，气足底面与平台之间形成一层气膜，将飞行器浮起，飞行器只受到空气摩擦阻力及阻力矩。在偏航和滚转方向的失重模拟采用垂向配重及气浮导柱实现。航天飞行器在地面做微重力环境的物理仿真实验中，利用气浮平台实现竖直方向的重力模拟；利用单自由度弹簧振动系统配合气浮台，模拟扭摆杆；采用单自由度弹簧激振装置，设计限位机构保证系统只有一个自由度。

2.1 偏航转动惯量测量原理

将气浮平台浮起并经过水平调整后，在其两端安装两组弹簧，可将飞行器视为一个单自由度弹簧振动系统[5]。测试时保证气浮平台振幅小于5°，以满足微幅振动条件，整个系统的振动方程为：

(2)

原方程化为：

(3)

其特征方程：

(4)

特征根为：

(5)

1) 过阻尼情况ζ>1

原方程通解为：

(6)

此时系统的运动按指数规律衰减，很快就趋近于平衡位置，不会产生往复的振动现象。从物理意义上看，由于阻尼较大，由初始激励输入给系统的能量很快就被消耗掉了，系统来不及产生往复振动。

2) 临界阻尼条件ζ=1

s1=s2=-ωz

(7)

θ(t)=(C1+C2t)e-ωzt

(8)

临界阻尼的通解通过Matlab仿真如图4所示，运动规律依然按照指数形式衰减，振动特性不明显。

3) 小阻尼ζ<1

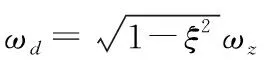
通解为：

θ(t)=e-ξωzt(C1cosωdt+C2sinωdt)

(9)

化简后得

(10)

通过Matlab仿真不同阻尼条件下的单自由度振动系统通解振动曲线可得，在弱阻尼的情况下，振动周期保持较好。

(11)

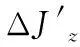
(12)

保持系统刚度一致，即Kz不变的情况，振动方程为：

(13)

测得对应的系统振动固有频率

(14)

附加配重后系统的振动周期为：

(15)

系统绕轴线Oz的偏航转动惯量的表达式：

(16)

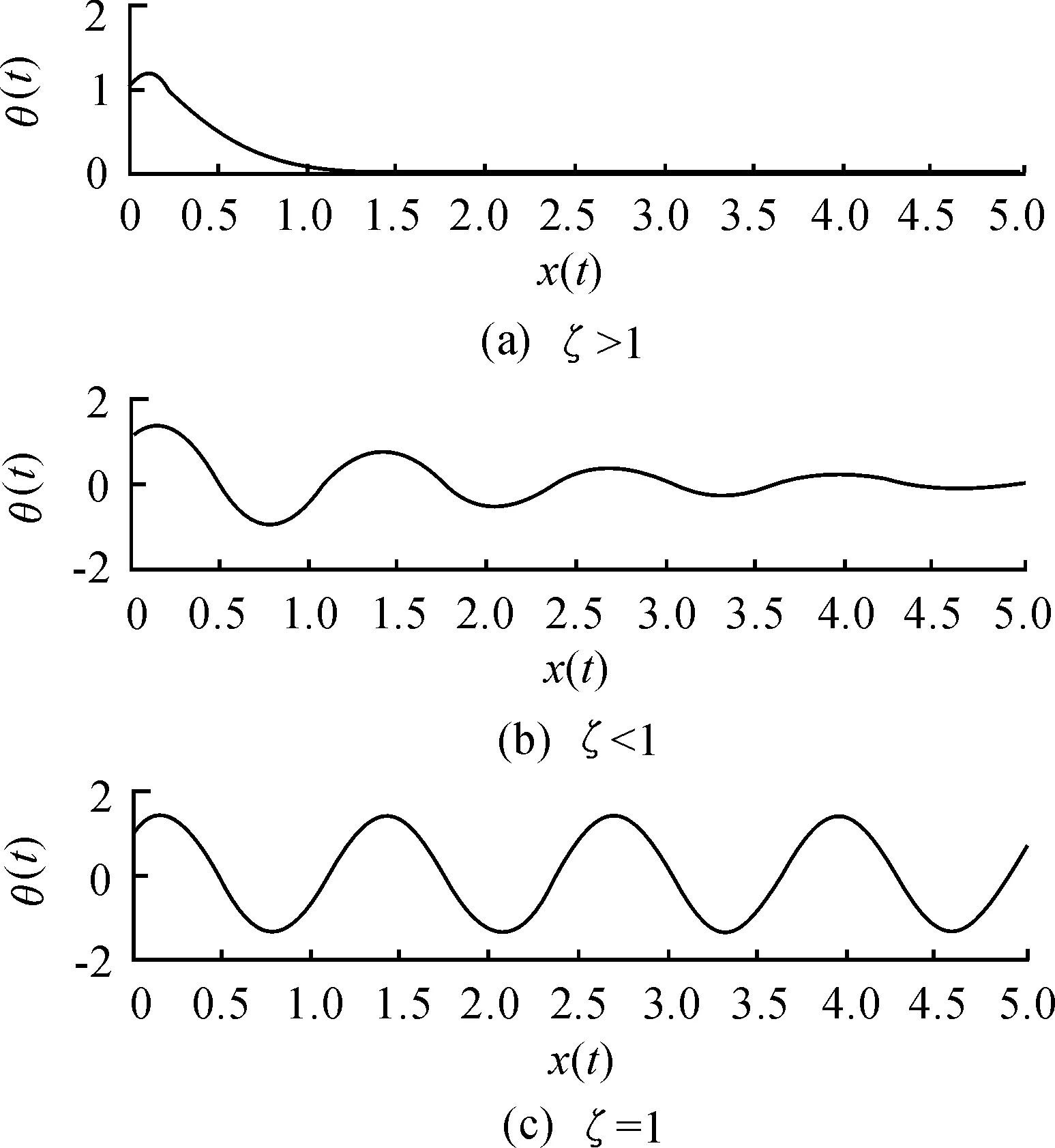
图4 不同阻尼比情况下的自由振动位移时程曲线

2.2 俯仰-滚转转动惯量测量原理

性能台航天飞行器俯仰转动惯量在线校准方案，航天飞行器的俯仰运动由二维转台和伺服电机控制。二维转台的安装位置为构件的质心位置，转台与飞行器之间由轴承连接。此外，支撑整个系统的气浮平台不作运动，对俯仰转动惯量不造成影响，实际测量中可以忽略。在弹簧振动上方设计一个转动限位机构，限制二维转台绕Ox轴的滚转运动，同时锁死气浮台等设备，使飞行器绕Oy轴进行俯仰运动的转动。根据现有结构特点，采用类似测量偏航转动惯量的弹簧振动法，得系统绕轴线Ox的滚转转动惯量的表达式：

(17)

同理可以绕轴线Oy的俯仰转动惯量表达式为：

(18)

3 在线校准装置设计

3.1 在线校准装置整体框架

转动惯量在线校准装置的工作原理为：振动单元提供激振源使性能台飞行器作微幅摆动，起振器使做均匀摆动。限位机构使飞行器能绕指定轴摆动，通过距离测量单元获得标准质量块的位置数据；通过摆动周期测量单元获取飞行器摆动周期数据。标准质量块质量特性参数通过测量机构测量得到。通过三大单元的参数获取，基于转动惯量计算式，计算相对应的转动惯量值，实现对弱撞击式对接机构对接性能试验台航天飞行器转动惯量的在线校准。图5是性能台航天飞行器转动惯量校准原理框图，虚线框中是转动惯量在线校准装置框图。

图5 性能台转动惯量在线校准装置总体框图

3.2 研建飞行器摆动周期测量单元

飞行器转动惯量测量中，摆动周期的测定是关键参数。本文测量摆动周期用光电测量法，在气浮平台等被测构件上安装遮光板，遮光板中线经过整个系统的回转中心(即飞行器的质心所在旋转轴)。当被测飞行器作摆动运动时，在构件上安装的遮光板将从光源射入光电传感器的光线档住。由于光线明暗相间的变化，使光电传感器产生一个光电脉冲信号。光电传感器输出电脉冲信号送到触发电路，经过放大器整形，输送到数字频率计，获得飞行器的摆动周期参数。摆动周期测量单元原理框图如图6所示。图7和图8所示的是性能台飞行器偏航转动惯量和俯仰/滚转转动惯量振动周期校准装置示意图。

图6 摆动周期测量单元原理框图

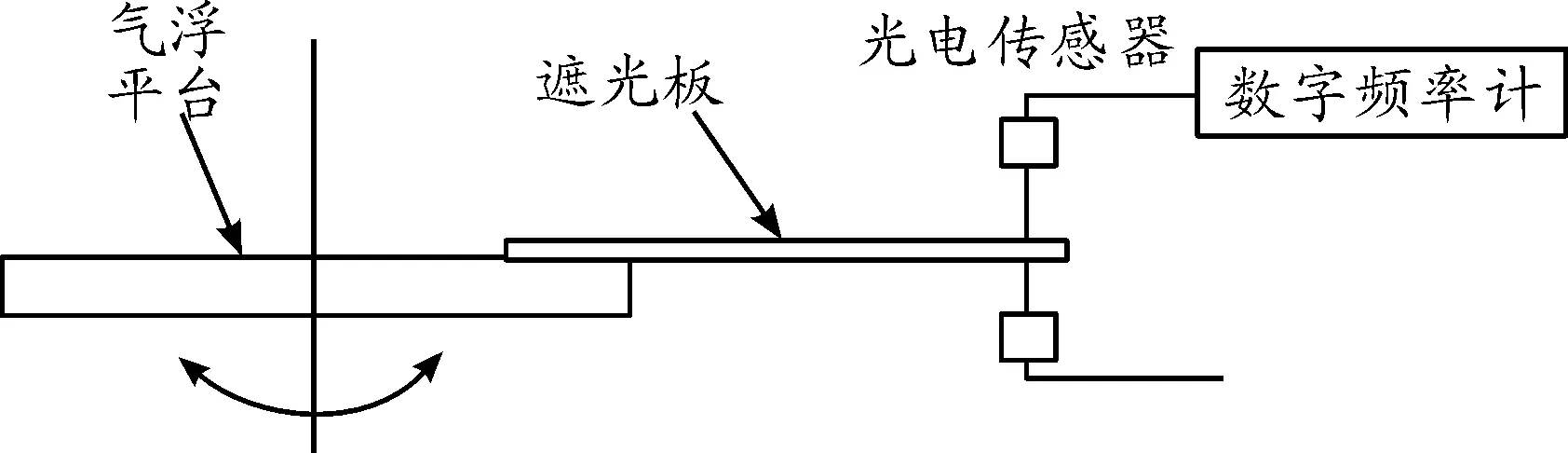
图7 偏航运动转动惯量摆动周期校准示意图

图8 滚转/俯仰运动转动惯量摆动周期校准示意图

3.3 研建飞行器距离测量单元

飞行器转动惯量在线校准中，标准质量块质心与摆动轴的距离L的测定是一项关键参数，本文拟采用位移传感器进行测量。距离测量单元的框图如图9所示。

图9 距离测量单元原理框图

3.4 研建飞行器标准质量块

飞行器转动惯量在线校准是基于附加质量配重方法，通过在性能台航天飞行器的主梁和配重杆上附加标准质量块，根据转动平行轴定理，可知飞行器构件增加的转动惯量主要由标准质量块自身转动惯量和距离回转轴距离产生的附加转动惯量组成。标准质量块安放在性能台航天飞行器的主梁和配重杆上，距离回转轴距离较大时，可以获得较大的附加转动惯量。综合考虑试验台航天飞行器质量以及主梁与配重杆的长度，选取不超过主动飞行器质量5%与不超过被动飞行器质量10%标准质量块组。根据设计的校准方法，拟转动惯量校准所用的标准质量块质量为20 kg，被动飞行器转动惯量的校准所用的标准质量块为5 kg。拟研制的标准质量块如图10所示，主要技术参数如表2所示。图10中箭头方向为计算标准质量块自身转动惯量的回转轴方向。

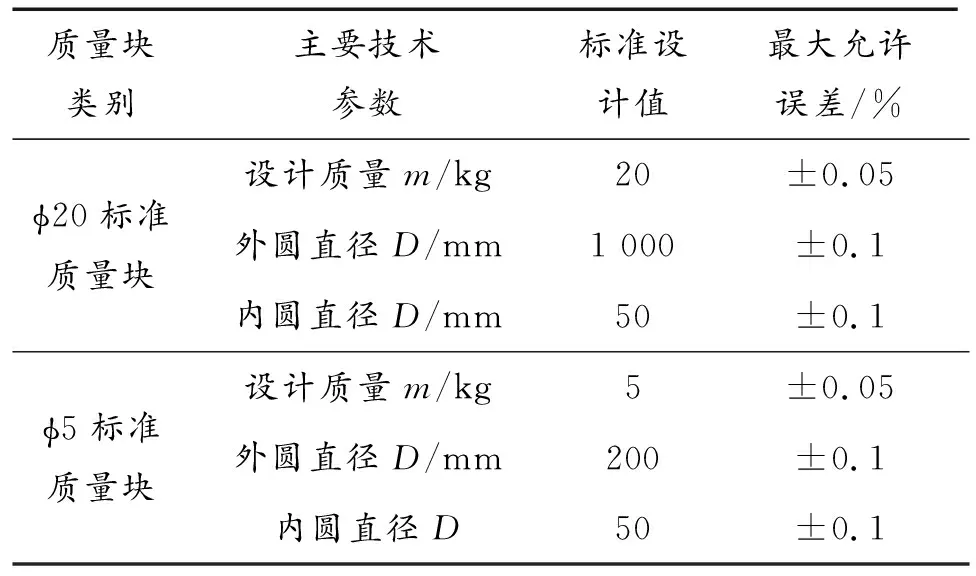
表2 标准质量块主要技术参数

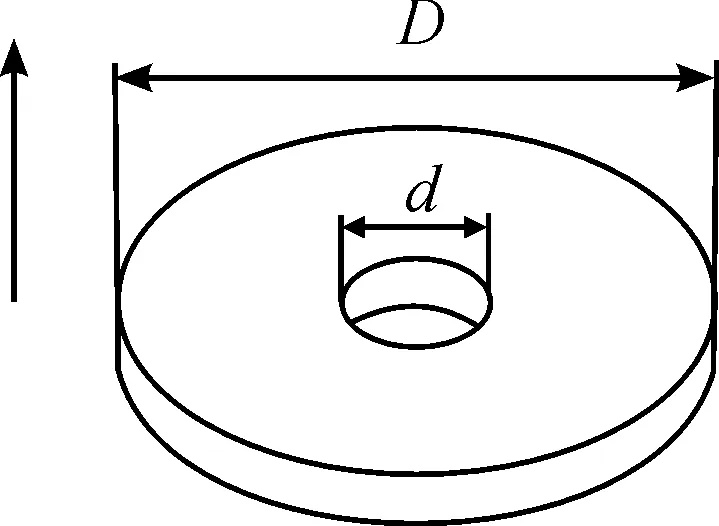
图10 标准质量块

3.5 研建飞行器运动限位机构

在对性能台测量时，必须让航天飞行器绕某一特定回转轴(回转轴经过飞行器的质心)进行微幅摆动或振动，才能进行转动惯量摆动周期的测量，计算转动惯量的值[6]。

本研究针对性能台航天飞行器的结构特性和实际安装状态，根据性能台本身的特点，研制与之配套的能够开展转动惯量测试的两套限位机构，限位机构不仅承担转动惯量在线校准装置振动单元。转动惯量摆动周期测量设备的固定和支撑，而且要确保航天飞行器能够严格按照转动惯量在线校准要求绕特定回转轴进行摆动，从而实现转动惯量的在线校准。由于飞行器本身结构复杂，是整个对接性能试验台的一大组成构件，其结构尺寸较大，而且是漂浮在气浮台上，因此限位机构的研制是本研究的一个难点。

由于航天飞行器整个系统的质心位置设置在二维转台垂直轴线上，设计一套平动限位机构限制气浮平台的二维移动，使其只做偏航运动。将限位机构的限位中心设置在二维转台处，使整个系统的质心落在回转轴线(方向铅锤)Oz上,如图11所示。

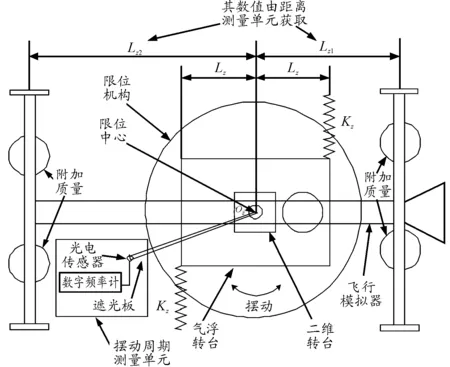
图11 偏航转动惯量在线校准示意图

在进行飞行器俯仰转动惯量和滚转转动惯量测量时，需要利用飞行器质心位置的二维转台进行绕Y轴和X轴进行微幅振动。由于二维转台能够同时进行绕Y轴和X轴的自由转动，因此需要利用限位机构将某一方向的转动进行限制，确保进行转动惯量在线校准时，飞行器只进行绕指定回转轴的微幅振动。其原理如图12、图13所示。

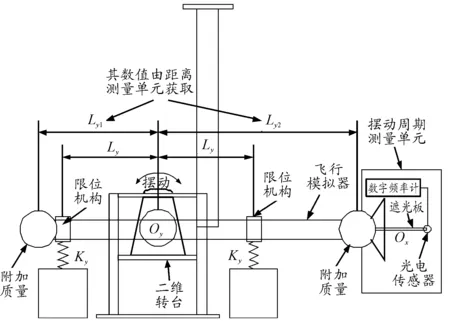
图12 俯仰转动惯量在线校准示意图

4 实验仿真及误差分析

4.1 ADAMS实验仿真

将模型导入ADAMS进行动力学仿真，在下端安装有单自由度弹簧振动系统，进行仿真，飞行器如图14所示[7]。

图13 滚转转动惯量在线校准示意图

图14 飞行器

在组建单自由度弹簧振动系统时，对于弹簧的选择尤为关键，在进行摆动时候，应该在弹性限度内进行微幅摆动，使满足胡克定律。对于不同的弹簧，应通过实验测得其弹性限度。保证在实验过程中所施加的作用力使得弹簧在弹性限度内工作。表3是对不同弹簧振动周期的动力学仿真。

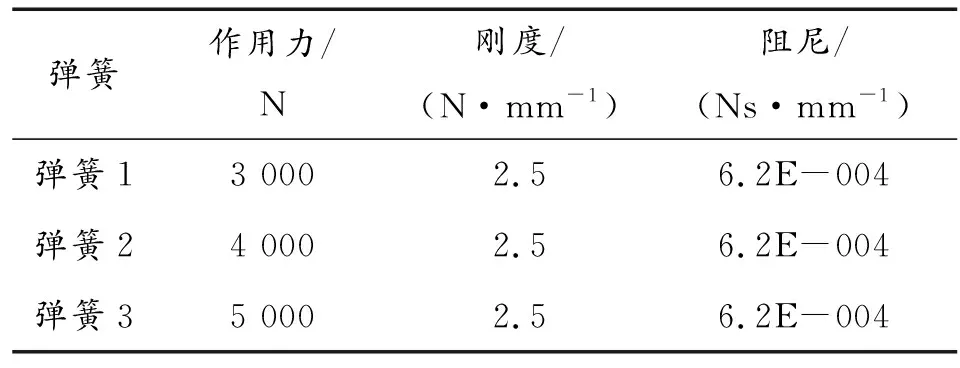
表3 不同初始力作用的弹簧参数

通过对图15曲线分析，不同的力使飞行器振幅不同，但对周期影响不明显。故选择初始力适中的值。

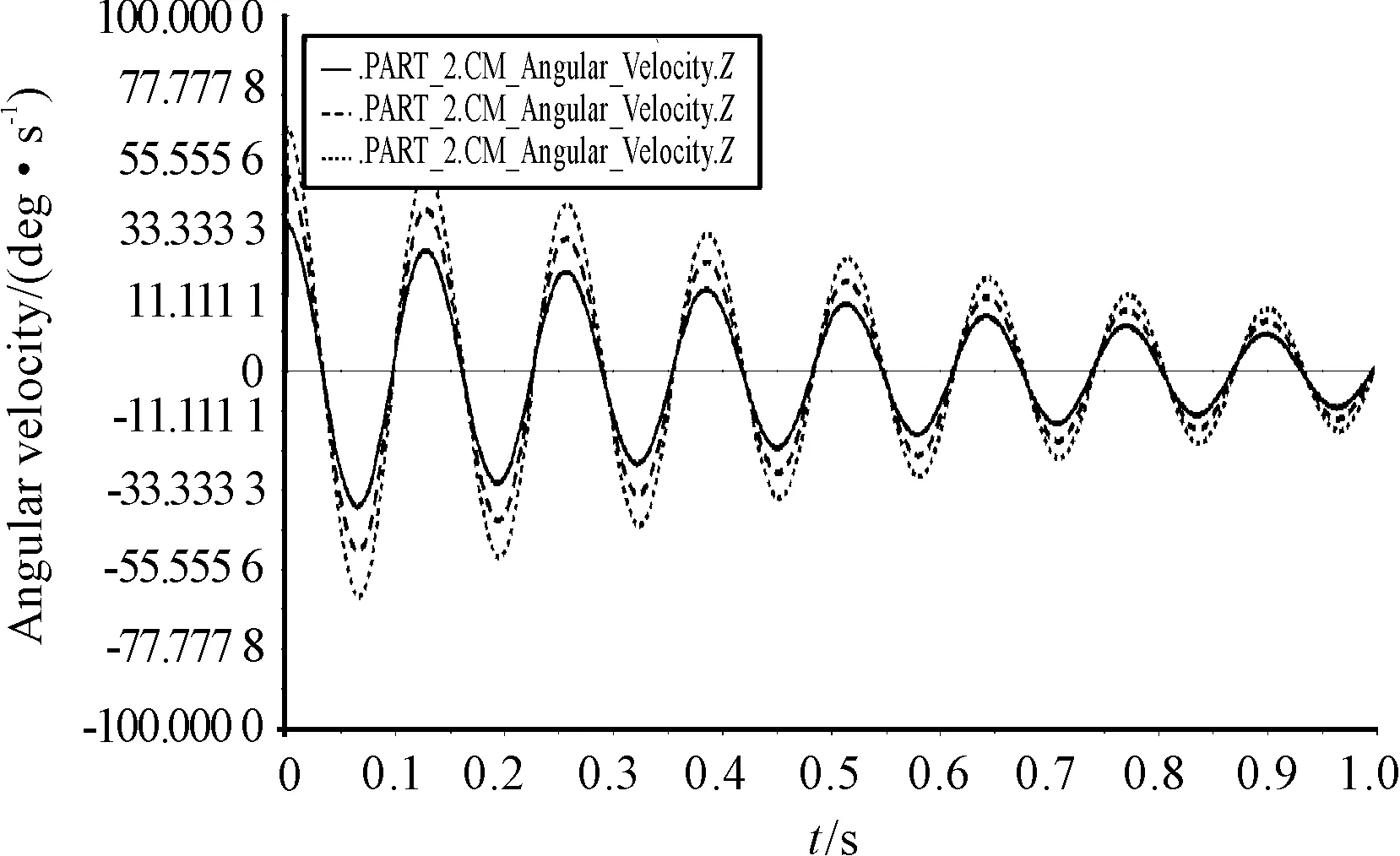
图15 飞行器振动角速度与初始力的关系

表4是不同刚度的弹簧参数。通过对图16曲线分析，不同刚度的弹簧使飞行器周期不同。刚度越大周期越短，测量误差更大，故选择刚度适中的值。

表4 不同刚度的弹簧参数

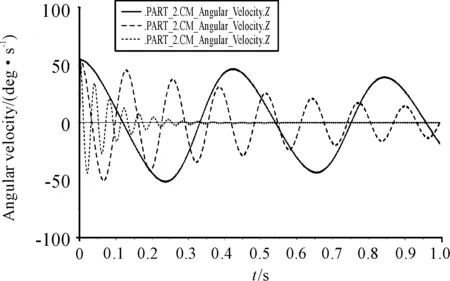
图16 飞行器振动角速度与刚度的关系

表5是不同阻尼的弹簧参数，通过对图17曲线分析，不同阻尼的弹簧使飞行器振幅不同。但对周期影响不明显。故选择阻尼较小的值。

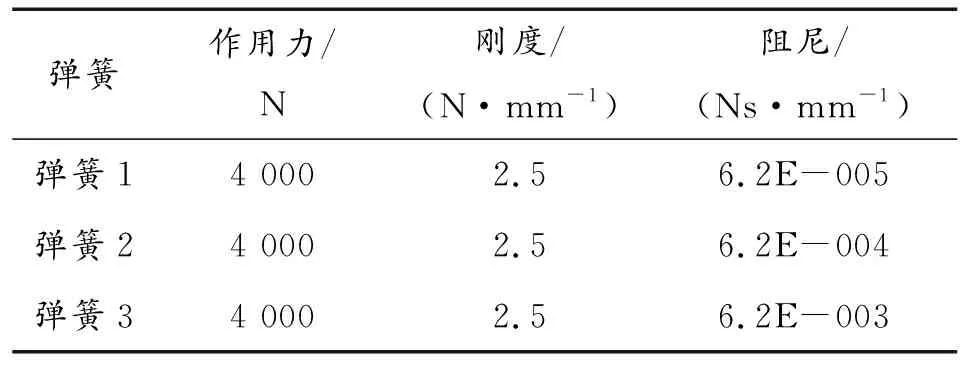
表5 不同阻尼的弹簧参数

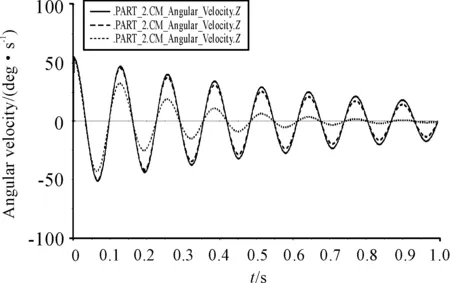
图17 飞行器振动角速度与阻尼的关系

4.2 测量不确定分析

根据上述性能台航天飞行器转动惯量的在线测量方法和数学模型可知，转动惯量校准的测量不确定度影响因素主要有标准质量块的质量偏差、标准质量块绕自身轴线转动的惯量的测量误差、摆动周期测量误差、质量块质心与回转轴距离的测量误差以及质心偏差引起的转动惯量测量误差等[8]。以偏航转动惯量为例，对式(16)所确定的转动惯量进行不确定度分析有：

(17)

即附加质量块相对回转轴的转动惯量误差引入的不确定度分量和测量摆动周期(含周期变化量)误差引入的不确定度分量。由式(12)可知，附加质量块相对回转轴的转动惯量的误差取决于质量m，距回转轴线的距离L和相对自身的转动惯量ΔJ1′。因此，ΔJz的误差为:

(18)

(19)

式中：T/2为理论半周期；T′/2为实际测量的半周期；R为光电管距回转中心的距离；θ为摆角；δ为遮光片宽度。该误差的大小与遮光片宽度δ成正比，与摆角θ和R成反比。式(19)经整理，可得摆动固有频率的理论周期为:

(20)

由于回转中心的距离R远大于δ，即误差的大小实际与摆角的大小成正比，当摆角控制在5°内时，实测周期与理论周期的误差可以确保在0.1%以内[9]。

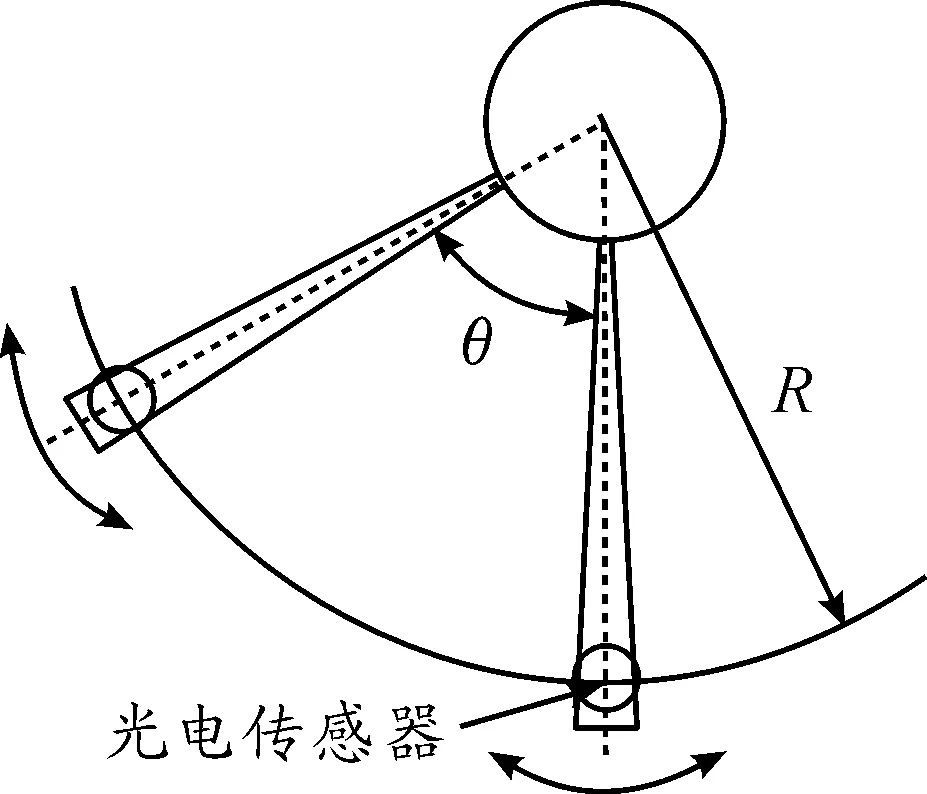
图18 遮光板误差分析简图

由式(15)可知，摆动周期Tz的误差与为弹簧至回转轴线的水平距离Lz有关(弹簧刚度的误差由附加质量法消除)，而转动惯量的测量与其无关但会影响摆动周期，因此误差主要来源于弹簧安装时与飞行器支承部件角度位置偏差。ΔLz为水平距离Lz引入的误差:

(21)

其中:α为弹簧与垂直于飞行器支承部件的法线之夹角，δ为水平距离Lz的相对减小量。由式(11)可知，摆动周期Tx与弹簧至回转轴线的水平距离Lz成正比。当α为1°以内时，误差可以控制在0.02%以内。摆动周期Tz的误差与摆动周期测量单元测量仪器设备引入的误差有关。通过以上分析可知，飞行器转动惯量的测量不确定度不会影响确保满足要求[10]。

5 结论

本研究分析了基于扭摆法的转动惯量在线测量方法,利用ADAMS有限元分析软件完成了弹簧对于转动惯量测量影响的仿真,结合具体现场实验得出以下结论:该转动惯量在线测量方法能够很好地保证测量精度，尤其针对大型非回转体有很好的适应性。本文中弹簧刚度和空气阻尼均为线性,而在实际实验中,必须防止扭摆角度过大超过弹簧线性刚度。