舰载机牵引系统的动力学建模与仿真
2018-07-31范加利朱兴动宋建华
范加利,朱兴动,宋建华,王 正
(1.海军航空大学青岛校区, 山东 青岛 260041; 2.海军航空大学训练部, 山东 烟台 264001)
转运作业是舰载机舰基保障的重要组成部分,在飞行甲板或机库甲板,舰载机的转运作业由牵引车顶推或牵引实现。目前,世界各国航母的舰载机转运主要依靠有经验的牵引车驾驶员操纵牵引车完成。随着驻舰舰载机种类和数量的增加,牵引车操纵频繁,这就对牵引的安全性和快速性提出了更高的要求。
为了便于后续开展舰载机牵引系统的路径规划和跟踪方法的深入研究,本文针对牵引系统运动速度低、牵引车、舰载机和牵引杆之间的铰接角较大,舰载机参数差异大,牵引系统同时存在完整约束和非完整约束等特点,基于物理特性和机械运动的基本概念,建立牵引系统通用模型。首先,以有杆牵引车组成的牵引系统为对象,根据非完整约束特性,引入广义速度,建立系统的运动学模型,然后,通过适当地定义质量和角速度矩阵,采用经典的牛顿-欧拉方程描述系统动力学特性,模型推导中不需考虑两个铰接点处的力和力矩。最终获得的模型可以作为使用无杆牵引车的舰载机牵引模型特例。
1 国内外研究现状
舰载机调运是航母舰载机舰基保障的重要环节,它影响着舰载机的出动强度,对航空战斗力生成具有重要作用。
近年来,国内外学者对舰载机调运问题进行了大量研究。从相关文献报道看,大致分为舰载机牵引轨迹控制与牵引技术虚拟训练[1-3]、舰载机舰面调运路径规划[4-7]以及舰载机调度[8]。这三个方面研究既有区别,又有联系。舰载机调度问题是从最顶层规划舰面保障资源,最优安排舰载机的布列、转运、机务保障等各个环节。舰载机路径规划主要研究甲板环境下,如何移动舰载机达到时间和安全性最优,它是研究调度问题的基础。舰载机牵引系统的路径控制关注舰载机路径的实现,它与路径规划问题相关。
本文的研究内容是舰载机路径规划与路径跟踪控制的基础。关于舰载机牵引系统模型方面的研究,文献[1-2]建立了舰载机牵引系统的侧向运动模型,研究了牵引系统的行驶稳定性和自动转向控制问题,文献[4],在相关假设下,建立了牵引系统的运动学模型,研究了舰载机的避碰监视,文献[5],基于舰载机的运动学模型,研究了舰载机甲板避碰路径规划。上述文献中建立的舰载机牵引系统模型均具有一定的局限性。舰载机牵引系统属于一类具有非完整约束特性的多体铰接系统,系统动力学和运动学分析较为复杂,文献[9-11]对该类系统进行了大量研究,取得可供借鉴的结论。
2 牵引系统建模
2.1 运动学模型
飞行甲板上,使用有杆牵引车牵引舰载机的示意图如图1。
取牵引车后轴中心坐标为(xt,yt),舰载机主轮中心坐标为(xa,ya),牵引杆与牵引车纵轴线间的夹角为β1,牵引杆与舰载机纵轴线间的夹角为β2,舰载机和牵引车的航向角分别为θa和θt,牵引车前轮转角为δ,牵引车纵向速度为vt,lt为牵引车前后轮轴之间的轴距,lb为牵引杆长度,lt为舰载机前轮与主轮之间的距离,c1为牵引车后轴距牵引车尾钩的距离。建模中做如下假设:
(1)整个牵引系统在甲板面做平面运动,且舰载机和牵引车各轮运动中均无滑动。
(2)牵引车和舰载机的运动和动态均关于各自的纵轴对称。
(3)牵引系统中各机轮与甲板面的接触连续,即作业过程中机轮均不离开甲板面。
(4)牵引车与牵引车和舰载机的铰接点无摩擦。
(5)忽略甲板的复合运动对舰载机牵引系统的影响。
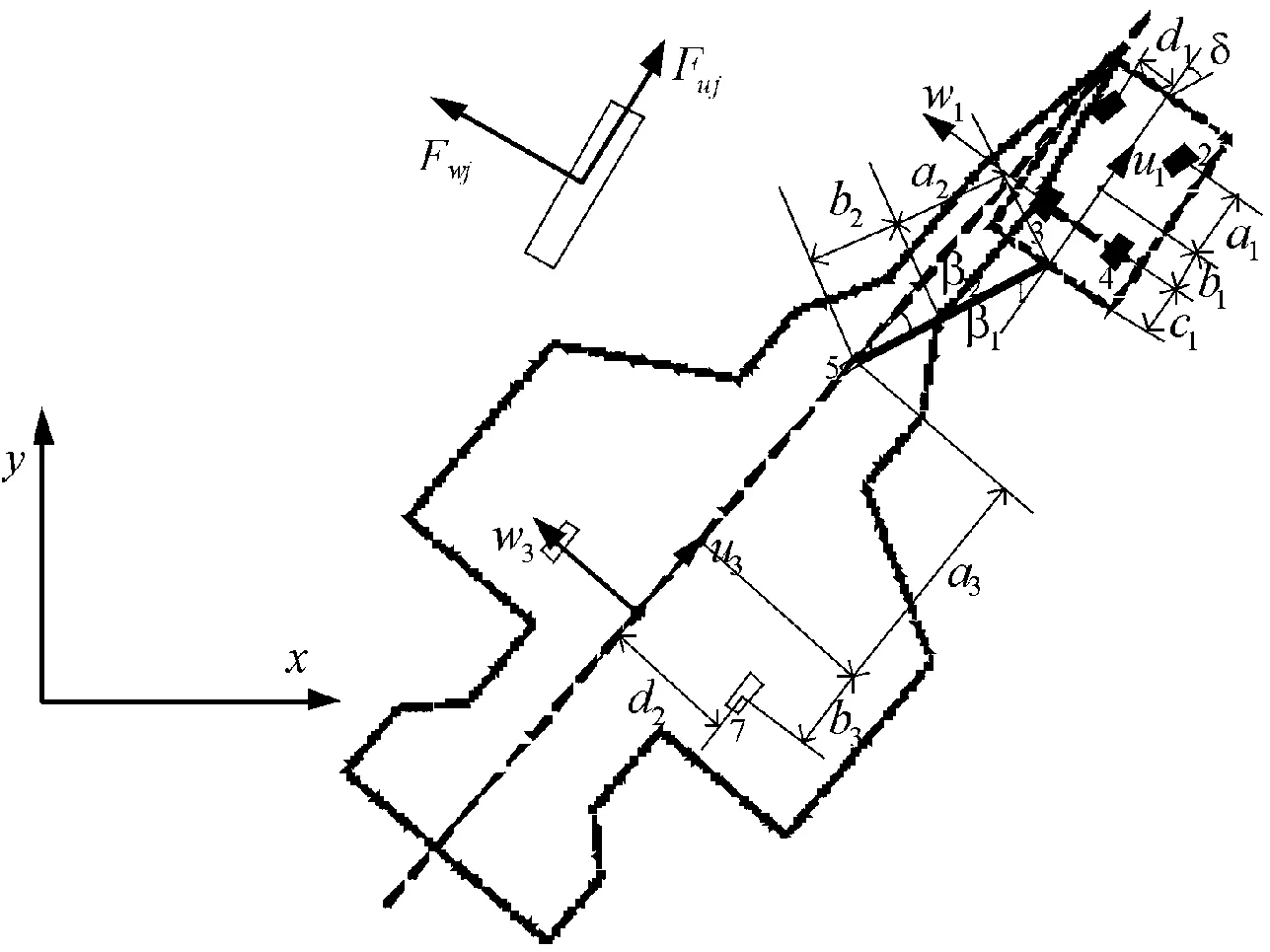
图1 舰载机牵引示意图
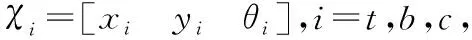
xa=xt-c1cosθt-lbcos(θt+β1)-lacos(θ+β1+β2)
ya=yt-c1sinθt-lbsin(θt+β1)-lasin(θ+β1+β2)
θa=θt+β1+β2
(1)
其中,lb=a2+b2,la=a3+b3。
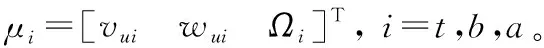
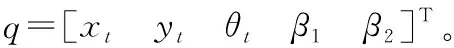
(2)
其中:
在假设式(3)条件下,根据系统的非完整约束特性,可定义标量广义速度α=vut。建立系统的运动学模型为
(3)
其中:
考虑系统实际存在的机械约束,牵引车前轮转角δ、牵引车纵轴与牵引杆之间的夹角β1以及牵引杆和舰载机纵轴之间的夹角β2均存在机械约束,即:
|β1|≤β1max,|β2|≤β2max
(4)
|δ|≤δmax
(5)
2.2 动力学模型
根据式(2)和式(3),速度向量μ和广义速度的关系即:
μ=Jh(q)Jnh(q,δ)α=J(q,δ)α
(6)
其中J(q,δ)为:
(7)
定义牵引系统中每一部分的扩展质量矩阵为Mi=diag(mi,mi,Ji),i=t,b,a,定义M=diag(Mt,Mb,Ma),其中mi是第i个部分的质量,Ji每一部分相对于各自重心的转动惯量(在平面内绕各自纵轴旋转),类似地,定义扩展的角速度矩阵:
且W=diag(Wt,Wb,Wa)。
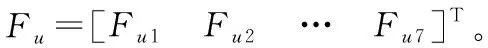
Fui=μaNi
(8)
μa是滚动摩擦因数,Ni是个轮胎承受的垂直载荷。
主动力和力矩向量见式(9)。
(9)
利用上述表达式,可计算惯性力、向心力和哥氏力分别为:
D(q,δ)=JT(q,δ)MJ(q,δ)
(10)
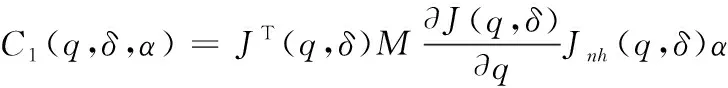
(11)
(12)
只考虑纵向速度的系统动力学模型为
JT(q,δ)Γu(δ,β2,Fu)}
(13)
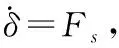
3 仿真研究
采用若干模拟设备,模拟舰载机、牵引车和牵引杆,模拟牵引车前轮转向,后轮驱动。牵引系统中各参数取值如下,a1=1 m,b1=1.4 m,c1=1.2 m,a2=b2=2 m,a3=4 m,b3=2 m,d1=1.15 m,d2=2.4 m,mt=3×103kg,mb=150 kg,ma=2.4×104kg,Ja=2 364 kg·m2,Jt=35 720 kg·m2。机械约束取值为:β1max=1.2 rad,β2max=0.78 rad,δmax=0.3 rad。
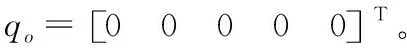
在Matlab环境下,基于文中建立运动学模型,研究牵引系统的运动学特性。牵引系统参数和初始位姿不变,对牵引车转向角取为δ=0.1δmax时,分别仿真牵引和顶推作业的系统响应,结果如图6~图8所示,从图中可以发现此时系统仍按圆弧路径机动,但圆弧半径明显增多,顶推时,β1和β2仍很快达到饱和值。令δ=0,α=±1 m/s,在20 s时对β1角加入0.1 rad的扰动,仿真结果如图9~图13所示,从仿真结果可以看出,正向牵引时,系统能够克服夹角扰动,这对应于实际系统中舰载机发生侧向滑移的情形,而对于逆向顶推,存在扰动时系统立刻发散,呈现折叠效应。
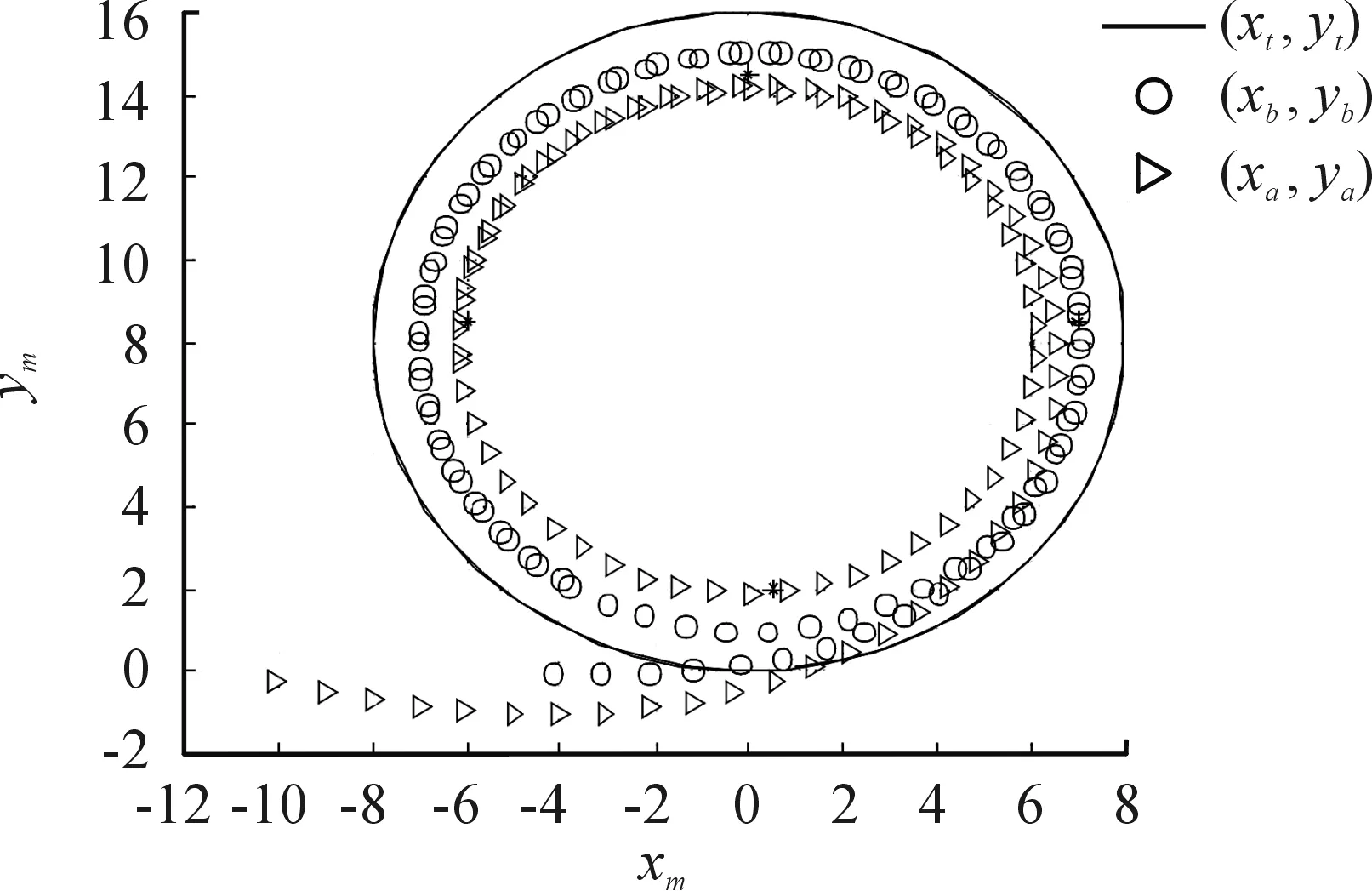
图2 正向牵引位置曲线
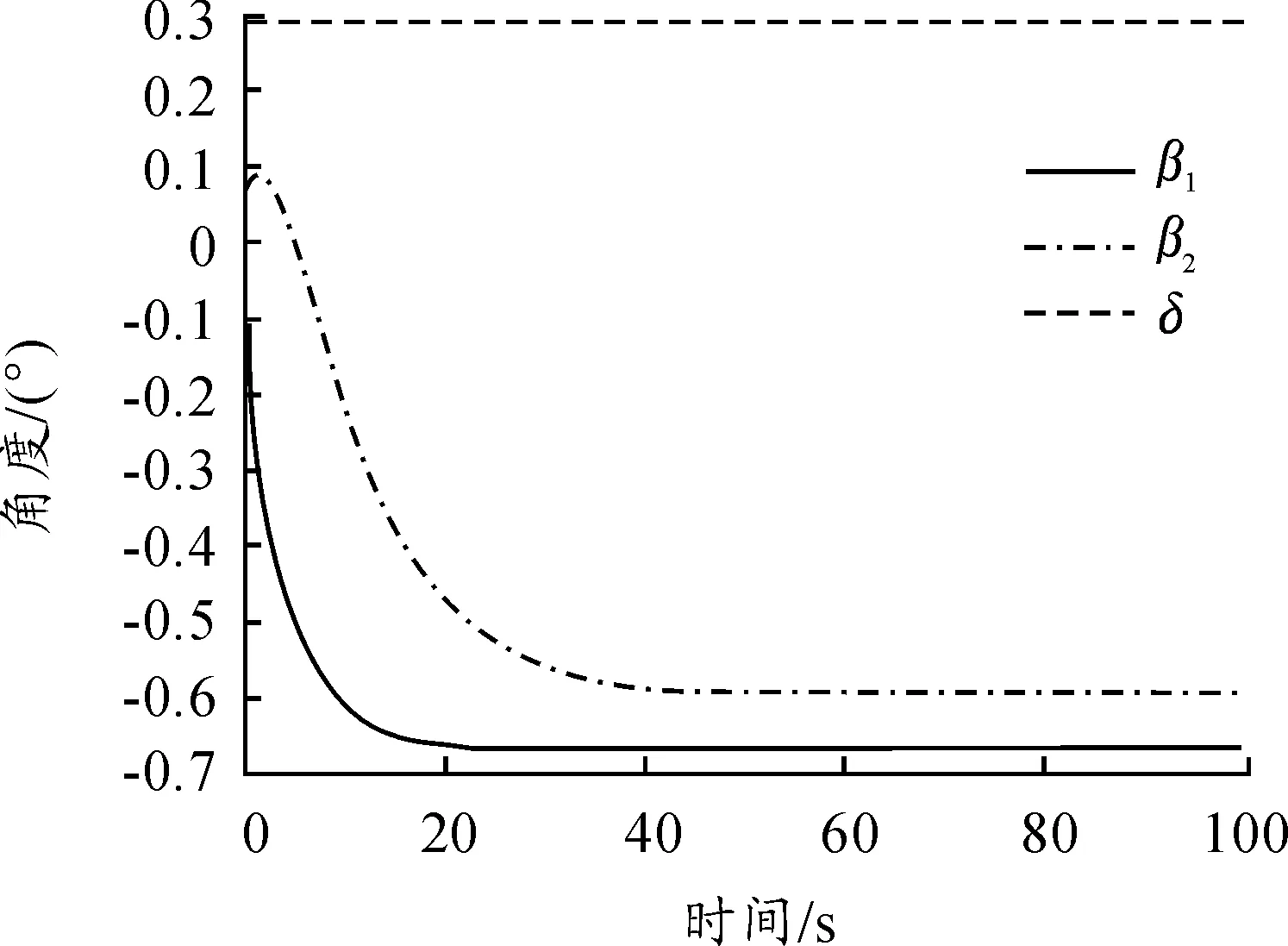
图3 正向牵引角度响应曲线
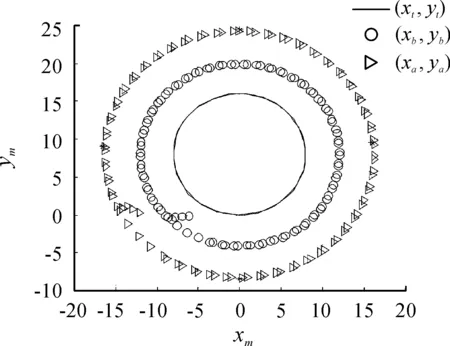
图4 逆向顶推位置曲线
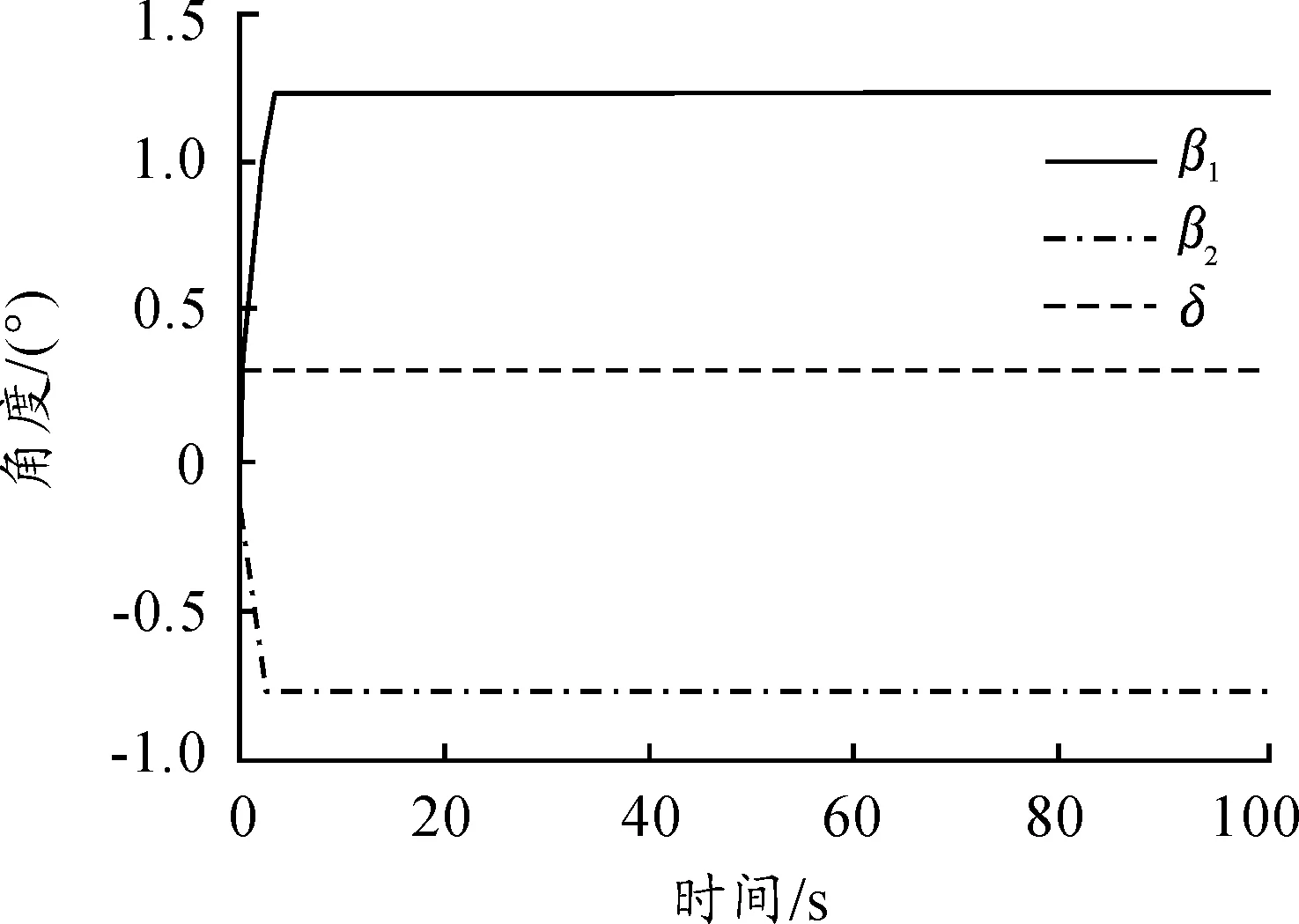
图5 逆向顶推角度响应曲线
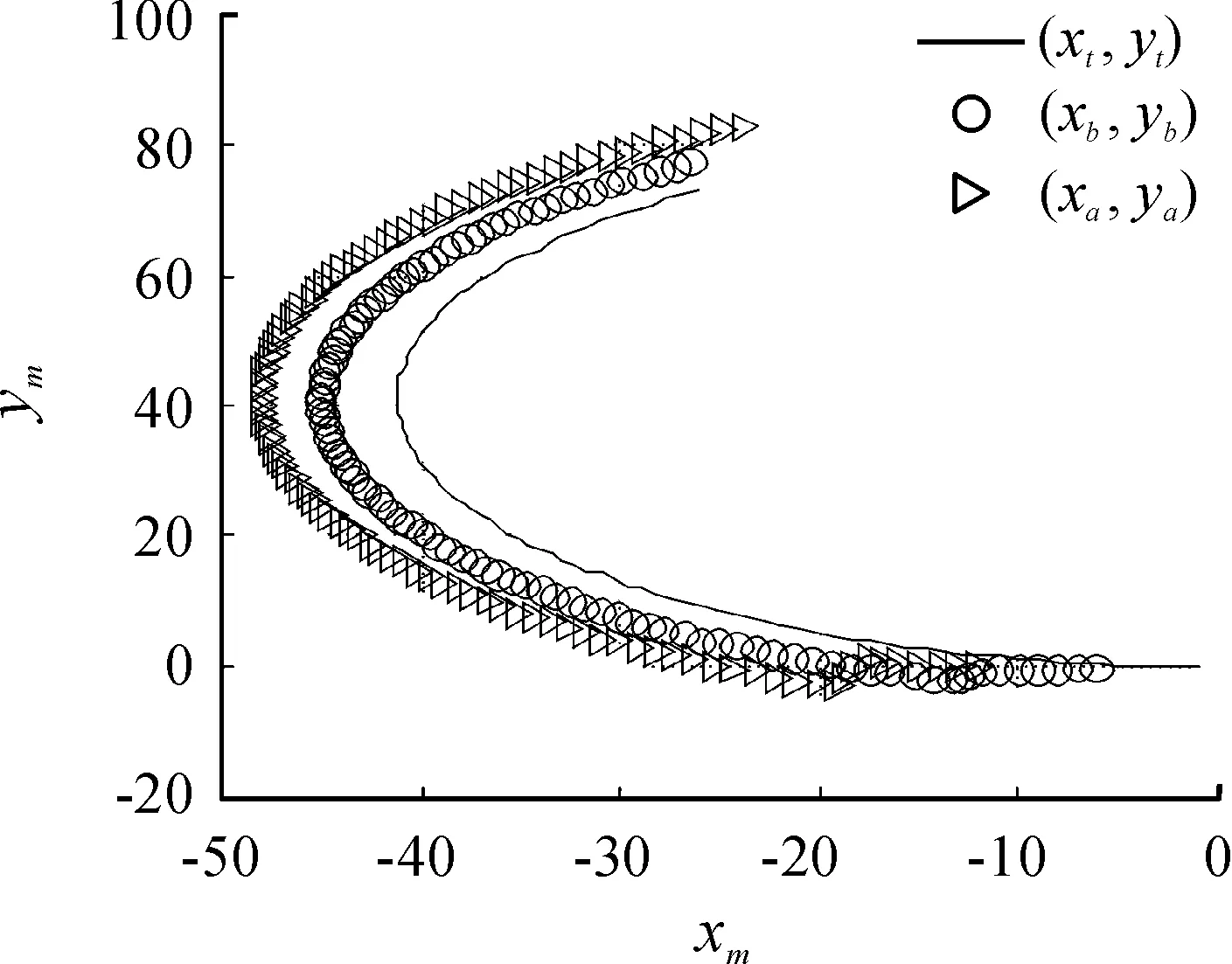
图6 δ=0.1δmax逆向顶推位置响应
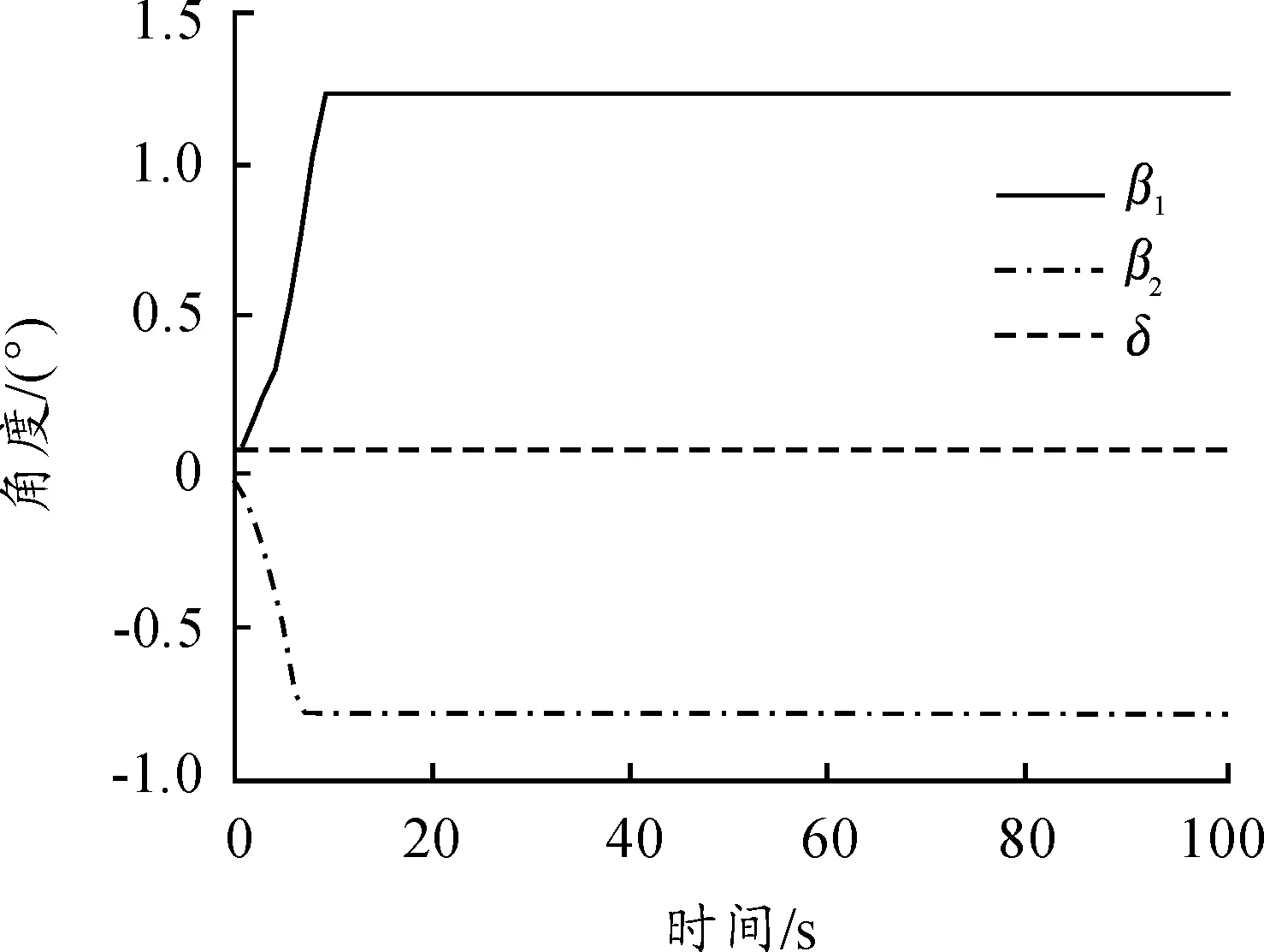
图7 δ=0.1δmax逆向顶推角度响应
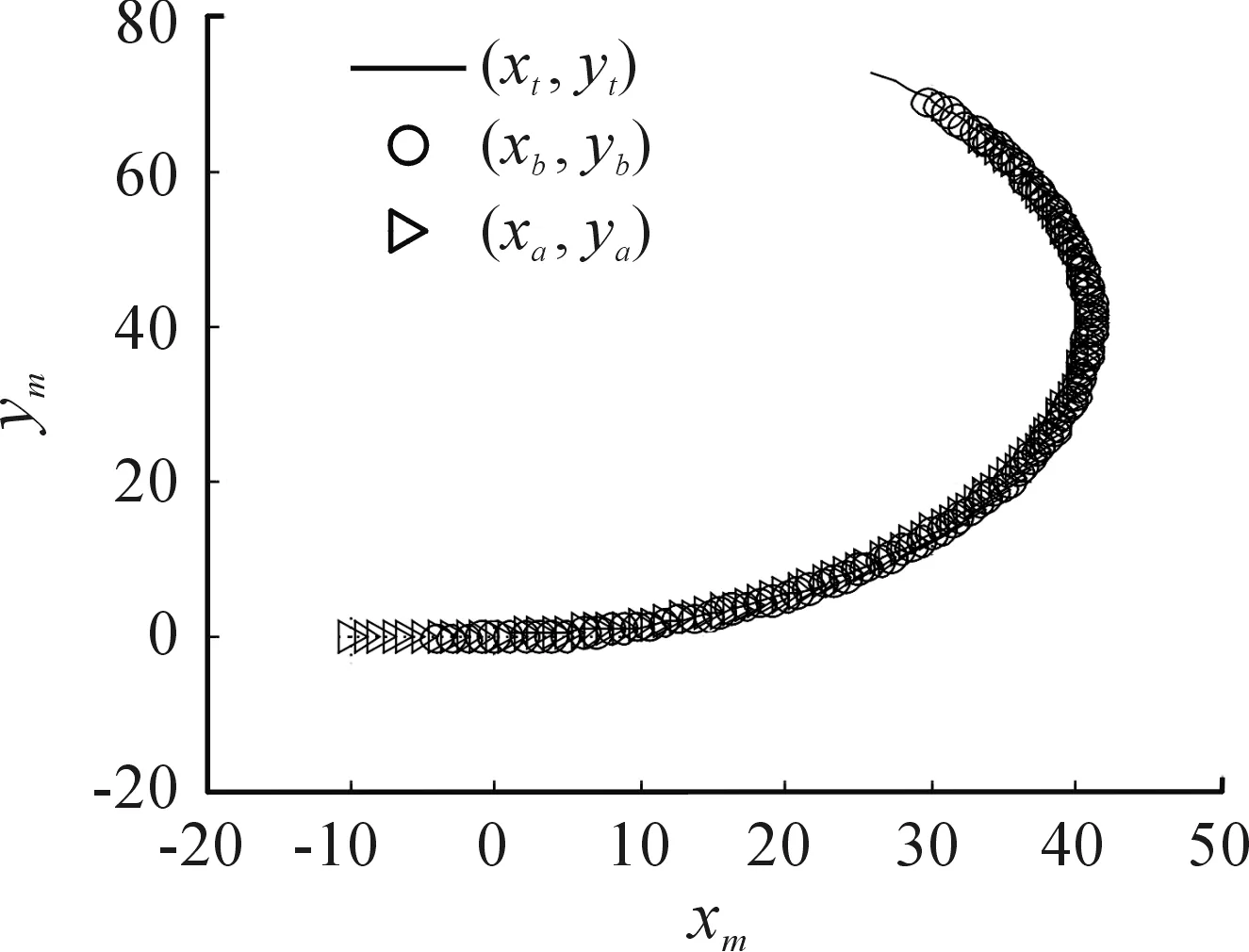
图8 δ=0.1δmax牵引位置响应
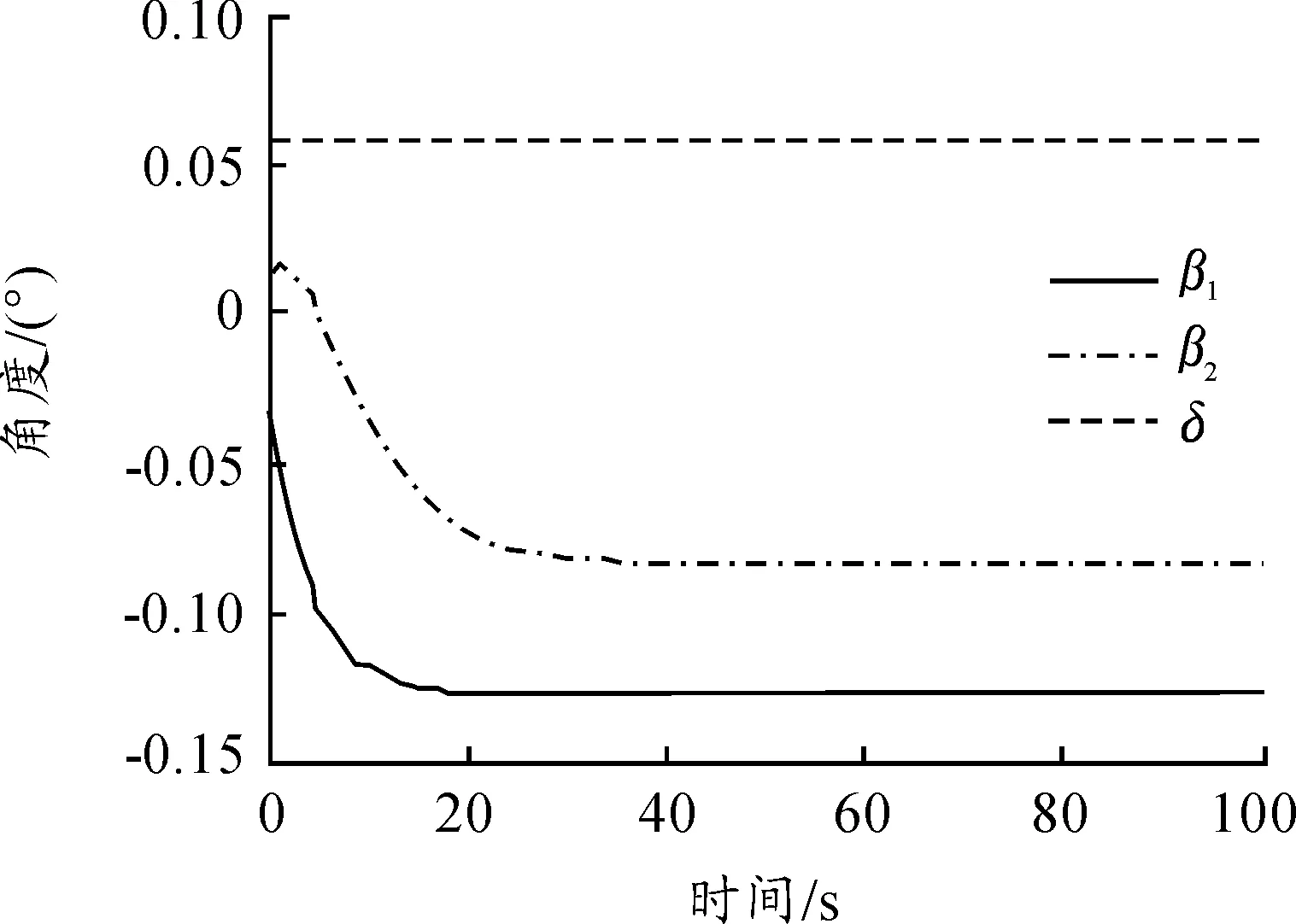
图9 δ=0.1δmax牵引角度响应
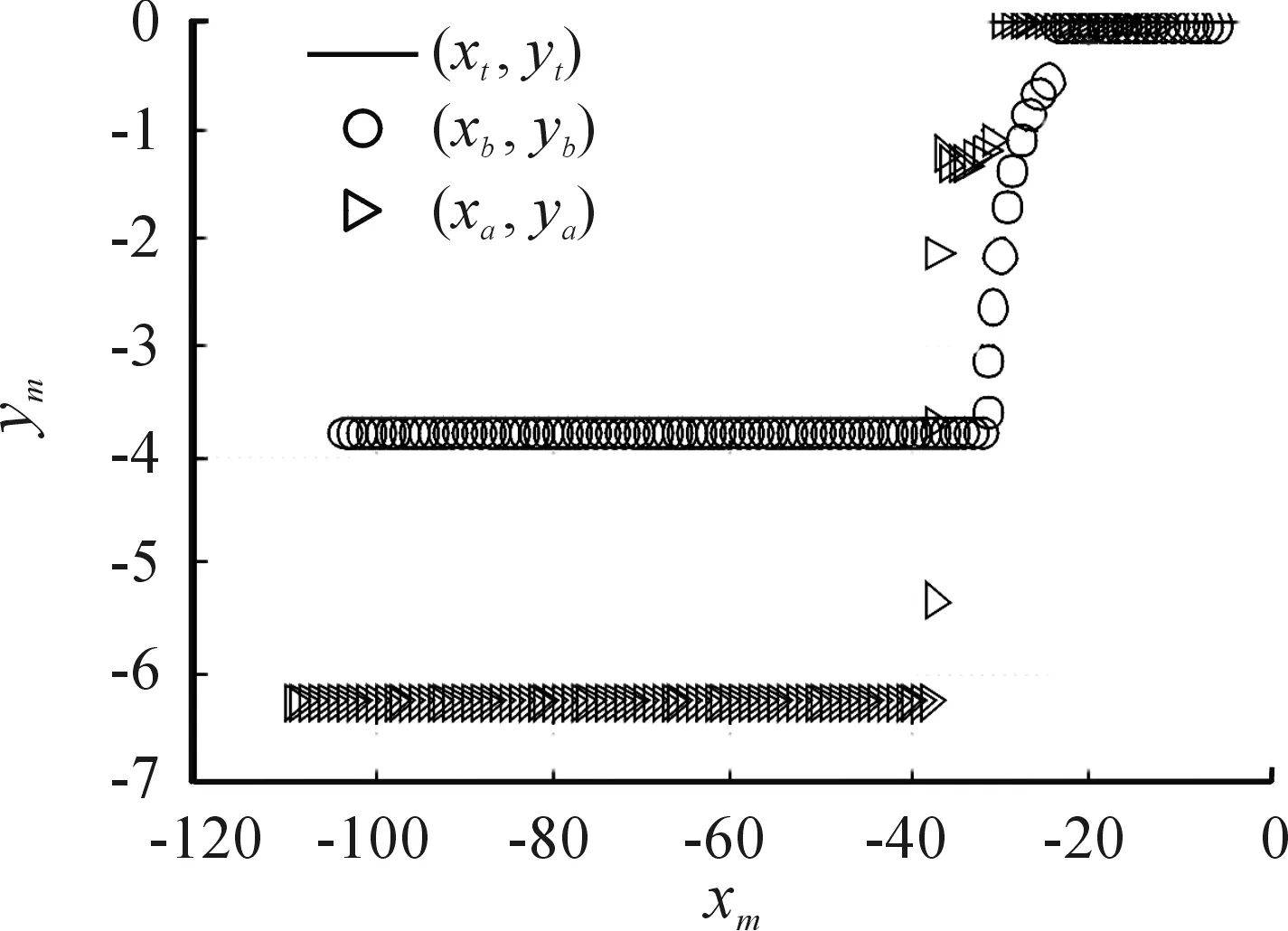
图10 δ=0顶推加扰动位置响应
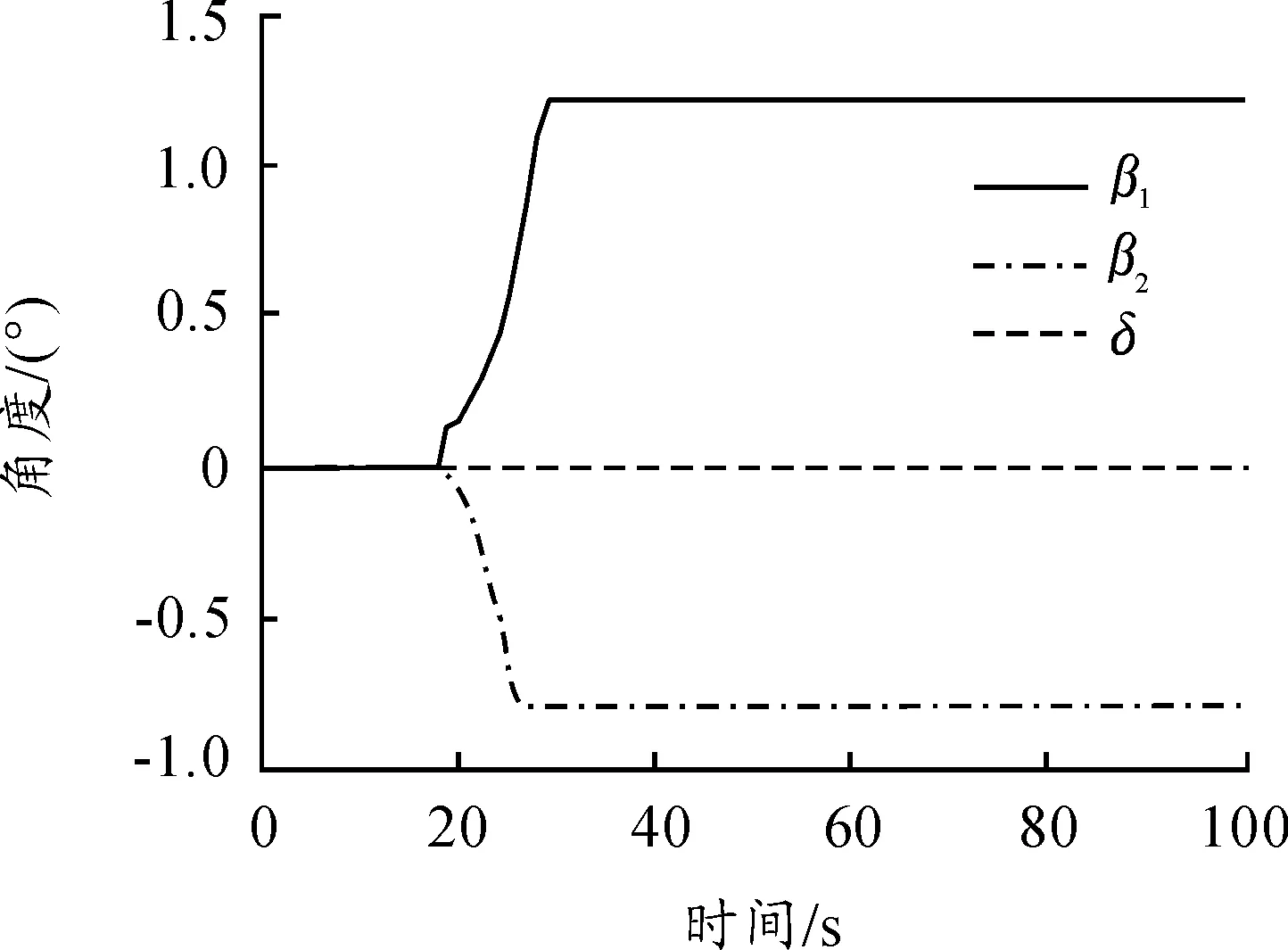
图11 δ=0顶推加扰动角度响应
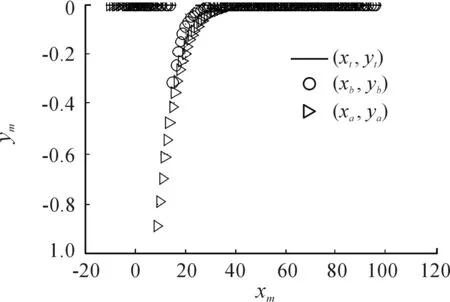
图12 δ=0牵引加扰动位置响应
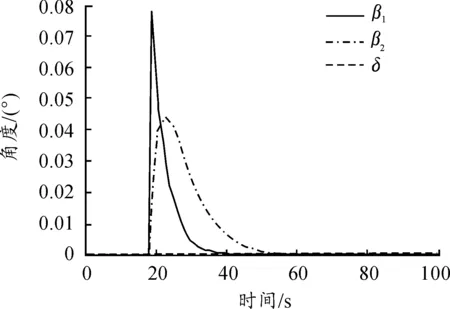
图13 δ=0牵引加扰动角度响应
4 结论
1) 验证了所建模型的正确性,该模型既适用于有杆牵引车牵引系统也适用于无杆牵引车构成的牵引系统建模。
2) 文中建立的模型适合用于舰载机牵引系统路径规划和路径跟踪的算法研究。舰载机牵引系统正向牵引时,系统处于稳定状态,可克服扰动,而逆向顶推时,由于折叠效应的影响,系统不稳定,要求牵引车驾驶员在顶推作业时必须及时调整牵引车前轮输入角,避免舰载机前轮长期处于极限转弯状态。
