欺骗干扰对防空导弹制导雷达影响分析
2018-07-31斗计华孙卫国
斗计华,孙卫国,吴 硕
(1.海军大连舰艇学院 导弹与舰炮系, 辽宁 大连 116018;2.海军91040部队教研室, 山东 青岛 266000;3.国防大学联合勤务学院 联合装备保障系, 北京 100858)
复杂电磁环境下防空导弹制导雷达工作时,其跟踪目标与制导防空导弹效果会受到欺骗干扰的影响。目前较多研究欺骗干扰[1-2]、对制导雷达的影响[3-4],较少定量研究欺骗干扰对防空导弹制导雷达的影响,本文根据防空导弹制导雷达工作过程,分析距离欺骗干扰和角度欺骗干扰对防空导弹制导雷达的影响,为研究欺骗干扰对防空导弹制导雷达影响提供依据。
1 距离欺骗干扰对防空导弹制导雷达影响分析
防空导弹制导雷达在跟踪目标时都要进行距离跟踪,当制导雷达辐射脉冲到达目标时,装载在目标上的干扰机同时接收制导雷达信号并对制导雷达信号进行复制和放大。然后干扰机经过一定的延迟发射复制的干扰信号,距离拖引开始,致使制导雷达将其作为目标回波信号进行跟踪。距离拖引干扰从类型上可分为后拖和前拖。后拖时,距离跟踪波门向距离增加的方向运动,产生目标背离制导雷达运动的假象;前拖时,距离跟踪波门向距离减少的方向运动。进行后拖干扰时,由于干扰机内部的延迟,干扰脉冲总比信号回波脉冲延迟一定量。
经一定时间的拖引后,干扰机短暂关机,拖引结束。设此时距离跟踪波门相对于目标回波信号的最大延迟时间为τmax[5],拖引时间为T,表示为:
(1)
(2)
式中:Vj为干扰脉冲移动速度;Tr为脉冲重复周期;Δt为干扰脉冲相对前一个周期的延迟时间。
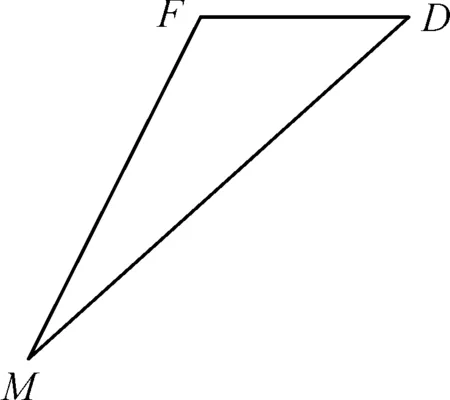
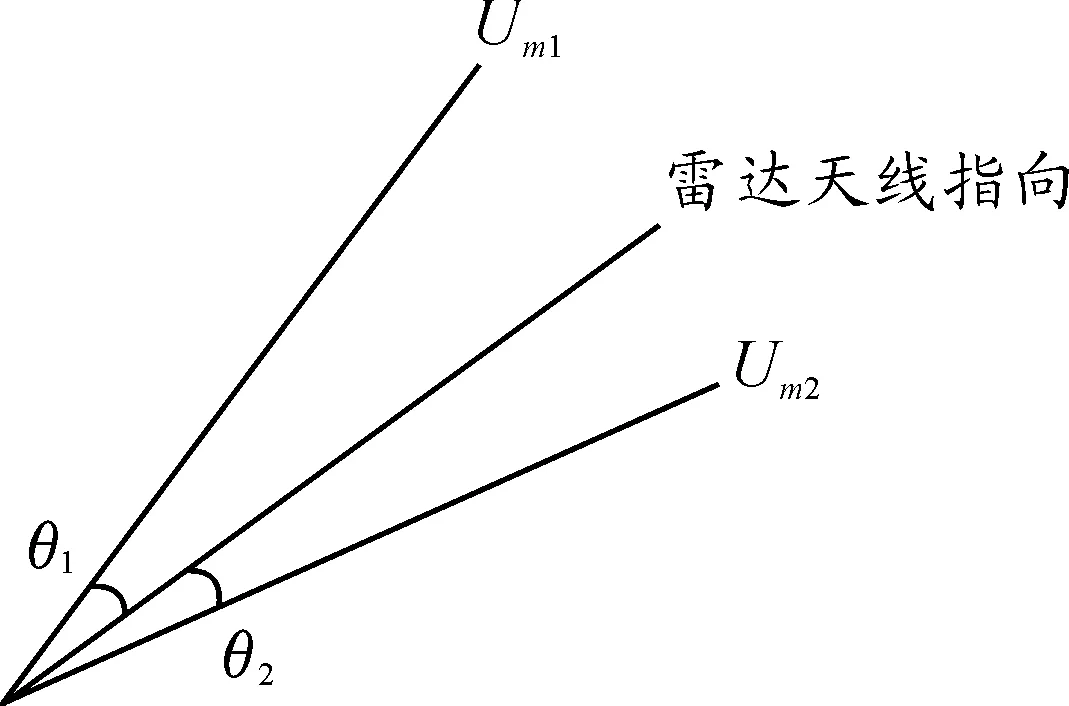
设防空导弹制导雷达距离跟踪系统的记忆跟踪时间为Tjy。当Tjy≥T时,距离欺骗干扰对制导雷达影响较小,制导雷达距离跟踪系统如果在Tjy期间能够捕获目标回波信号,就能跟踪上目标。当Tjy 角度欺骗干扰措施主要包括拖曳式诱饵干扰、交叉极化干扰等。 拖曳式诱饵干扰通常由飞机通过拖曳线缆将诱饵拖拽着飞行,拖曳式诱饵装有放大转发器和无源反射器,对制导雷达探测信号进行放大转发,与目标回波形成对制导雷达的双点源干扰,且双点源共处于防空导弹雷达导引头的瞬时波束范围内。实施干扰时制导雷达、目标、拖曳式诱饵的空间位置关系如图1所示,M为制导雷达,F为目标,D为拖曳式诱饵。 图1 制导雷达、目标和拖曳式诱饵的空间位置关系 假设双点源信号分别为Uj1、Uj2,可表示为: Uj1=Um1cos(ωt+φ1) (3) Uj2=Um2cos(ωt+φ1+Δφ) (4) 式中:Um1、Um2为两个信号的振幅;ω为信号角速度;φ1为初始相位;Δφ为两个信号相位差。 相干干扰原理是利用相隔一定距离的两个点源信号在幅度上相等,相位相差为常数时,在制导雷达天线口面空间产生极为严重的相位波前失真。当Δφ为常数时,双点源为相干干扰;当Δφ为变量时,双点源为非相干干扰。制导雷达接收到相干信号后,使制导雷达天线跟踪点偏离两个干扰源。干扰源与制导雷达天线电轴方向的空间关系如图2所示。 图2 拖曳式诱饵与制导雷达天线方向轴空间关系 当两个同频、相位相干的干扰源作用于制导雷达时,制导雷达天线电轴方向为: (5) 式中:θ1为点源1和制导雷达天线连线到天线电轴方向的角度;θ2为点源2和制导雷达天线连线到天线电轴方向的角度。 (6) 根据式(6)可得到以下结论: 1) 当Um1=Um2,即β=1时,无论Δφ为何值,恒有θ1=-θ2,制导雷达天线方向轴始终瞄准双点源的连线中心。 2) 当Um1≠Um2,且Δφ=0时,θ1=-θ2·β2,即点源1和点源2相位相同时,制导雷达电轴始终瞄准双干扰源的能量中心。 3) 当Um1≠Um2,且Δφ=π时,θ1=θ2·β,即双干扰源相位相反时,制导雷达天线电轴始终瞄准双点源之外。 4) 当Um1≠Um2,且Δφ=π,β→1时,若β从小于1的方向逼近1,则制导雷达天线电轴将瞄准双点源右边很远的方向;若β从大于1的方向逼近1,则制导雷达天线电轴将瞄准双点源左边很远的方向。 根据式(6)可画出θ1/θ2~Δφ的曲线,如图3所示。 从图3中可以看出,以β=0.5的曲线为例。在Δφ=0~120°时,θ1/θ2在-1~0,说明制导雷达天线轴线指向双干扰源之间;在Δφ=120°时,θ1/θ2=0,说明制导雷达天线轴线指向点源1;在Δφ=120°~240°时,θ1/θ2在0~1,θ1与θ2同号,制导雷达天线轴线指向双干扰源的左边;在Δφ=240°~360°时,θ1/θ2在0~-1,θ1与θ2异号,制导雷达天线又指向双干扰源之间。Δφ在0~360°变化时,制导雷达天线轴线指向在干扰源1左右变化,即在能量大的点源左右变化。β为其他值时制导雷达天线电轴方向依旧遵循此指向变化规律,只是在β=1,Δφ≠180°时,θ1/θ2=-1,制导雷达天线轴线始终指向双干扰源连线中心。因为在β=1,且Δφ=180°时,双干扰源能量在天线处相互抵消,制导雷达天线可能失去跟踪方向。根据以上分析可得,相干双点源对制导雷达作用时,随着Δφ的变化,制导雷达天线轴线方向将在能量大的干扰源左右变化。当两干扰源能量相等时,制导雷达天线轴线始终瞄准双干扰源连线的中心。 图3 不同β值下θ1/θ2~Δφ曲线 当双点源对制导雷达进行非相干干扰时,Δφ为随机变量,用Δφ(t)表示,则式(6)变为: (7) 式中:Δφ(t)为在0~2π均匀分布的随机变量;cosΔφ(t)取值在-1~1变化,均值为0。 制导雷达天线在双点源作用下的跟踪方向,取决于制导雷达的跟踪特性。如果把一次探测脉冲的回波作为计算样本,由式(7)的得到的θ1与θ2关系也是随机的。如果把N次探测脉冲的回波作为计算样本,则计算公式为 根据施工环境有针对性地选择参与的人员和机械设备等资源,依据人、机资源满足施工作业环境要求的原则,泵站深基坑作业调用经验丰富的胜建专业化队伍,单体水工构筑物按安全风险、施工难度的大小分别调用江苏、山东队伍。统筹考虑布置作业场地,依据人体作业特征,机、料位置固定合理,确定最佳作业区域、作业方法、最低安全防护范围,统一调配所有的机械设备资源,力争在有限的资源内,优化配置,通过提升人员的操作水平来最大限度地保证人和机械设备的安全。 (8) 若样本空间足够大,则cosΔφ(t)趋于其均值0,则式(8)可变为: θ1=-θ2·β2 (9) 即对于同频相位非相干双点源干扰,在测角探测脉冲的样本足够多时,单脉冲雷达的天线电轴将指向双点源的能量中心。 防空导弹制导雷达天线除辐射预定极化的电磁波以外,还辐射非期望极化的电磁波,前者称为主极化,后者称为交叉极化,二者正交。交叉极化干扰是利用雷达天线主极化和交叉极化接收矢量之间的不一致性,发射与制导雷达工作频率相同、与制导雷达天线主极化正交的电磁波信号,干扰制导雷达的角度跟踪曲线,达到角度欺骗的目的。电磁波在接收天线上感应的开路电压为[6]: V=hTEi (10) 式中:Ei为回波的电场矢量;h为制导雷达天线在该方向上的有效接收矢量。 考虑到制导雷达天线的交叉极化特性,将h分解为主极化和交叉极化两个相互正交的分量,记为: h=[m(θ)·c(θ)·ejφ]T (11) 式中:θ为方位角;m(θ)和c(θ)分别为天线主极化和交叉极化的电压方向图;φ为交叉极化接收矢量与主极化接收矢量的相对相位差。 相应的回波信号电场也分为两个正交部分: E=[sm(t)·sc(t)]T (12) 将式(11)、式(12)代入式(10)可得: V=m(θ)sm(t)+c(θ)sc(t)ejφ (13) 在无交叉极化干扰的条件下: V=m(θ)·sm(t) (14) 对于幅度和差单脉冲测角雷达而言,制导雷达测量角度θ1可表示为: (15) 式中,km为制导雷达角度鉴别曲线,这一角度与目标真实角度一致。 当存在交叉极化干扰时,交叉极化分量可表示为: sc(t)=kejσsm(t) (16) 式中:k为干扰信号与目标信号的幅度比;σ为干扰信号与目标信号相位差。 同样,由于存在交叉极化干扰,制导雷达的测量角度θ2可表示为: (17) 其中: B=2k[m1(θ)c1(θ)-m2(θ)c2(θ)] C=[m1(θ) +m2(θ)]2+k2[c1(θ) +c2(θ)]2 D=2k[m1(θ) +m2(θ)][c1(θ) +c2(θ)] (18) 由式(18)可见,交叉极化干扰实质上是使制导雷达角度鉴别曲线产生畸变,增大测角误差,从而达到干扰效果。 复杂电磁环境对防空导弹制导雷达影响过程中,需要重点关注欺骗干扰对防空导弹制导雷达影响。本文主要分析距离与角度欺骗干扰对防空导弹制导雷达的影响,构建了拖曳式诱饵干扰、交叉极化干扰对防空导弹制导雷达的影响模型,可有助于定量分析复杂电磁环境对防空导弹制导雷达影响。2 角度欺骗干扰对防空导弹制导雷达影响分析
2.1 拖曳式诱饵干扰对防空导弹制导雷达影响分析


2.2 交叉极化干扰对防空导弹制导雷达的影响

3 结论
