某型迫榴炮内弹道优化设计
2018-07-31曾宪刚乔相信姜登维
曾宪刚,乔相信,李 嘉,姜登维,吴 放
(1.沈阳理工大学 装备工程学院, 沈阳 110159; 2.辽沈工业集团有限公司 检验中心, 沈阳 110159;3.南京理工大学 能源与动力工程学院, 南京 210094)
当今世界,越来越多的陆军正在组建轻型快速反应部队,这就迫切需要一种既可间接瞄准又可直接瞄准射击的火炮武器,以适应各种条件下的多种作战任务,满足陆军营以下火力支援战斗分队的需求。迫榴炮[1]是一种介于轻重武器之间的火力支援武器,被称为“轻武器火力的延伸、重武器火力的补充”,近些年来名噪一时,受到各国军队的高度赞许。
迫榴炮是在传统迫击炮和榴弹炮的基础上演变而来的,它综合了这两种传统火炮的特点,既可直瞄射击又可间瞄射击,其机动性和战场生存能力强,非常适合现代化战场作战的需要。目前,美国、俄罗斯、德国等西方发达国家均投入大量的人力物力财力积极研制迫榴炮以装备各自的陆军。
为了提高迫榴炮的性能,研究人员针对迫榴炮的内弹道优化问题开展了研究。Acharya R等[2]深入研究了迫击炮内弹道流场的数值模拟和计算方法。张泽峰等[3]基于迫榴炮内弹道模型,提出了迫榴炮水弹试验的装水质量确定方法。赵雨馨等[4]改进了迫榴炮内弹道模型中气体流量的计算方法,通过仿真和实验证明了该模型较经典模型的优越性。程林等[5]使用MATLAB对火炮内弹道过程进行了数值模拟,分析了各内弹道参数的变化规律,并验证了模拟的正确性。在内弹道优化算法方面,李克婧[6]分析了多目标遗传算法在内弹道优化问题上的优势,提出了更加符合实际工程的优化方案。程诚等[7]建立了内弹道二维两相流模型分析不同点火因素对内弹道性能的影响。张泽峰等[8]基于改进差分进化算法进行了内弹道参数优化,优化结果满足工程要求。近些年,遗传算法也在优化设计领域广泛应用[9],陈亚军等[10]基于遗传算法对内弹道参数进行优化,验证了遗传算法用于内弹道优化的可行性。
装药设计及内弹道计算在武器弹药系统的研制中占有极为重要的地位,是整个武器系统研制的先导。本文对某迫榴炮的内弹道装药进行了优化。其优化方法和优化结果对某迫榴炮设计具有十分重要的现实意义。
1 迫榴炮内弹道计算
本文在分析迫榴炮特殊的内弹道特点的基础上,在一些基本假设的前提下,建立了某迫榴炮内弹道经典模型,并进行了数值求解。
1.1 基本假设
a) 假定基本装药和辅助装药的燃烧服从几何燃烧定律,以二项式表示火药已燃百分数ψ、火药相对燃烧面积σ及火药相对已燃厚度Z的关系式,燃速式符合指数燃烧定律。
b) 假定火药的燃烧和弹丸的运动均在平均压力下进行。这实际上也是经典内弹道模型的集总参数假设。
c) 尾管未破孔前,基本装药在尾管内定容燃烧,当尾管内压力达到破孔压力,打开传火孔后,燃气从尾管中流出并点燃辅助装药。在基本装药尚未燃完前,按照基本装药和辅助装药构成的混合装药处理。基本装药燃完后,辅助装药单独燃烧,直至燃完。
d) 假定气体从间隙流出服从气体动力学的有关规律,即满足临界状态条件。
e) 热散失通过减小火药力的方法间接修正热散失系数。
f) 在射击过程中,炮管与弹丸定心部之间的间隙本来是偏心圆环,但为计算流量简单起见,视作同心圆环,即
SΔ=S-S1
(1)
式中:SΔ为弹炮间隙面积,S为炮管截面积,S1为弹丸定心截面积。对于某些装有闭气环的情况,可令SΔ=0。
1.2 迫榴炮经典模型
1) 尾管喷口未打开前,基本装药定容燃烧阶段模型[11]
(2)
式中:χ为火药形状特征量,u1为燃速系数、e1为火药弧厚,p1为尾管内压力,相当于高压室压力,f为火药力,ω为装药质量、Vd为尾管容积。
当尾管内燃气达到破孔压力pTK时,尾管的喷口全部打开,喷口的衬纸被剪切破坏,破孔压力可按材料力学理论确定,为
(3)
式中:b为衬纸的厚度;d1为尾管喷口的直径;τK为衬纸材料的剪切强度。
将式(3)代入到方程组(2)中的状态方程,则可以求出破孔时的火药相对已燃百分比ψ0,即
(4)
根据ψ0,由方程组(2)可求出Z0和t0,作为下一阶段的初始条件。
2) 基本装药和辅助装药混合燃烧阶段模型
本文根据火药燃烧、气体生成、状态变化、能量转换等燃烧和热力学过程,分析弹丸在膛内受力状态,建立包括燃烧方程、状态方程、流量方程、能量方程和弹丸运动方程等在内的经典内弹道模型[11]如下
(5)
初始条件为
t=0,v=l=η=0,τ=1,p=p0
ψ=ψ0=α1ψ10+α2ψ20
其中
式中 ΔT=ω1/V0;Δ2=ω2/V0;V0为药室容积;CT为热损失修正系数。
式中 Δ1=ω1/Vd。
式中 Δ2=(ω1+ω2)/V0。
1.3 计算结果及分析
内弹道曲线见图1、图2、图3和图4。图中可以看出,由于迫榴炮使用的火药很薄(4/1单基药),曲线表现非常陡直,以致最大压力点位置和火药燃烧结束点位置非常接近。文献[11]中同样条件的计算,得到了最大压力点和火药燃烧结束点完全重合的结果。从压力曲线的变化规律表明,迫榴炮的弹道性能应该具有较大的装药利用系数ηω和较小的炮膛工作容积利用系数ηg。
根据文献[11]中提供的某迫榴炮内弹道实验数据,用铜柱测压器测得的最大压力为40 MPa左右,按通常的铜柱测压和压电测压的换算系数N′=1.12,换算成压电测压的最大压力约为44.8 MPa。初速实际测量值为202~205 m/s。计算的最大压力为50.246 MPa,初速为204.618 m/s,计算值与实际测量值符合较好。
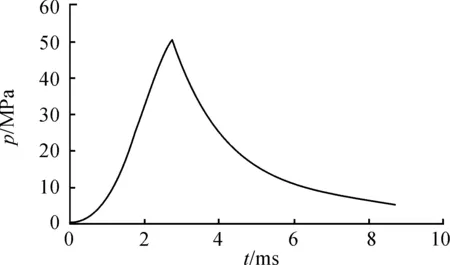
图1 某迫榴炮的压力-时间(p-t)曲线
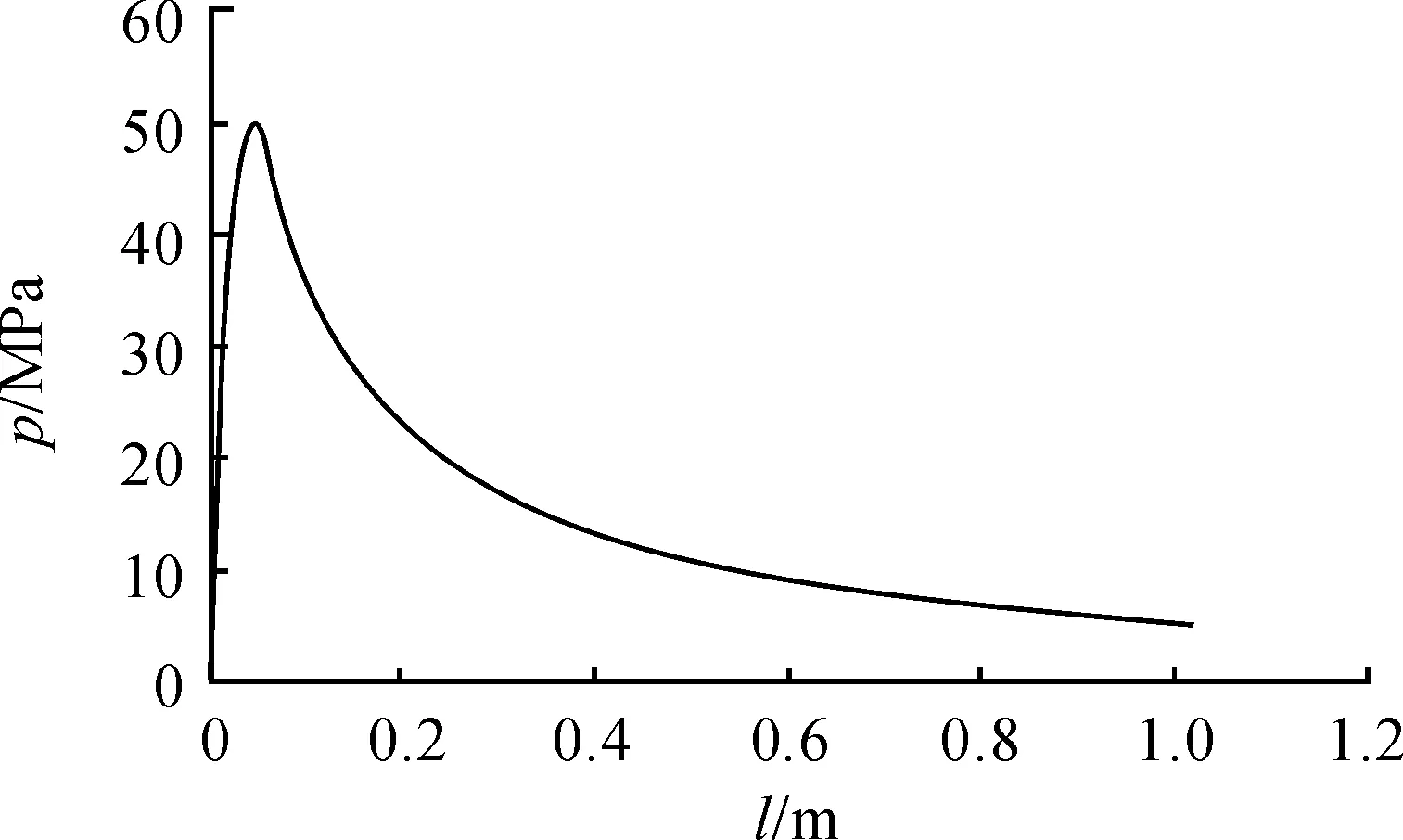
图2 某迫榴炮的压力-行程(p-l)曲线
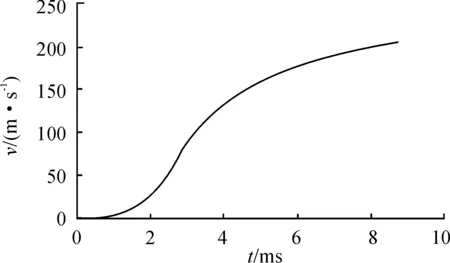
图3 某迫榴炮的速度-时间(v-t)曲线
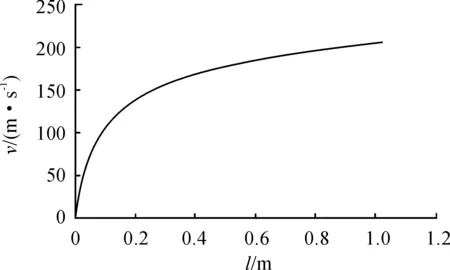
图4 某迫榴炮的速度-行程(v-l)曲线
1.4 不同因素对内弹道性能的影响
为研究不同因素对迫榴炮内弹道性能的影响,在保证其他条件不变的条件下,分别变化装药量、弹重、炮管间隙及药室容积,研究不同因素与迫榴炮最大膛压和炮口初速的关系。所得结果如表1所示。
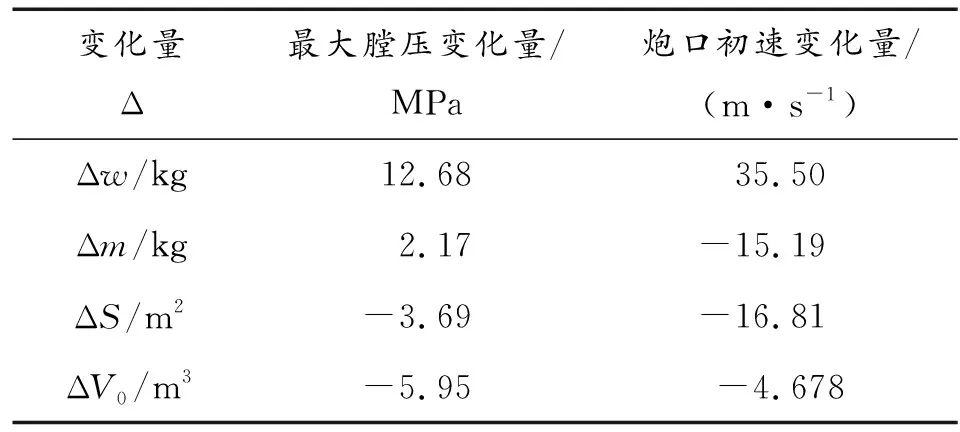
表1 最大膛压和炮口初速与各因素的关系
表1中装药量变化量Δw为0.01 kg,弹重变化量为1 kg,炮管间隙面积变化量为0.000 1 m2,药室容积变化量为0.000 1 m3。由表1可以看出,迫榴炮的装药量、弹重、炮管间隙及药室容积对其弹道性能的影响显著,且最大膛压和炮口初速对不同因素的敏感度也不一样,具体结果为:
a) 初速比压力对于装药量的大小更加敏感;
b) 初速比压力对于弹重的大小更加敏感;
c) 初速比压力对于炮管间隙的大小更加敏感;
d) 压力和初速对于药室容积大小的敏感度相近。
2 迫榴炮内弹道过程装药优化设计
内弹道优化设计的对象是内弹道过程,即在满足内弹道性能指标的条件下,寻求设计目标函数的装填条件和火炮结构诸元。
本文针对传统内弹道装药设计浪费大、效率低、周期长的缺点进行内弹道装药优化设计,以达到提高设计质量、缩短设计周期的效果。
2.1 优化问题的建立
本文根据一般的优化设计理论,结合迫榴炮的经典内弹道模型,选取最大压力pm作为约束条件,即pm≤[pm]许用。对于装填密度的约束,由于药室容积已认为为设计参数,所以它主要体现在装药量上,又考虑到辅助装药量占比很大,可把对装填密度的约束考虑到设计变量ω2的取值范围中,即把设计变量ω2的取值范围作为常量约束,最大压力pm作为函数约束,建立优化问题如下:
(6)
本文选择炮口初速vg作为最优化问题的目标函数,炮口初速vg是已选取的设计变量辅助装药的装药量ω2和辅助装药的火药半弧厚e12的函数。本文将在膛内最大许用压力pm许用的约束条件下,求解设计变量值,使炮口初速vg达到最大。
本文考虑到迫榴炮内弹道方程组的复杂性,选用复合形法优化求解。复合形法可求解的数学模型如下:
(7)
2.2 优化结果分析
根据上节所述的复合形法调优过程,在Visual Basic中编制复合形法的计算程序,求解方程组(6)。初始条件:ω2的优化范围0.040 5~0.1 kg,e12的优化范围为0.000 2~0.000 3 m,约束条件为pm≤75 MPa。计算结果如下:
a)ω2=0.072 829 04 kg,e12=0.000 274 94 m;
b) 约束条件下的最大速度vg=266.70 m/s;
c) 优化运行的迭代次数为37次。
图5为优化前后炮口初速曲线图。由图5可知,通过优化计算,弹丸速度整体增大,炮口初速有了较为明显的提高,较优化前速度提高了24.44%,较好地满足优化要求。
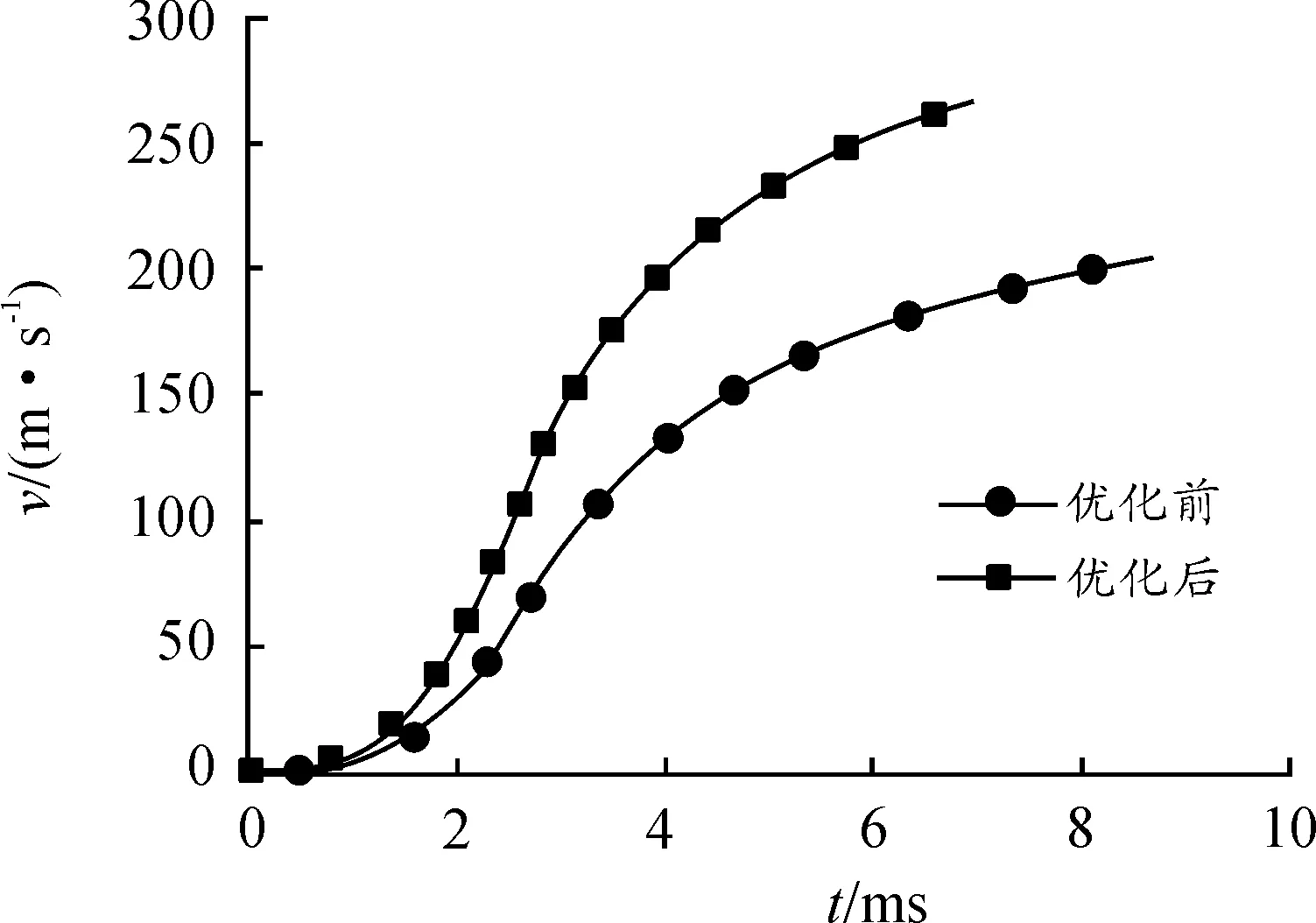
图5 优化前后炮口初速曲线
由以上优化分析结果可知,在满足约束条件下,能够实现对对炮口初速的优化设计,且优化过程所需的迭代次数较少。因此,通过优化设计,可以得到了更加合理、科学的内弹道参数设计方案。
3 结论
本文针对某迫榴炮进行了内弹道计算,分析了不同因素对弹道性能的影响;又采用复合形法对其进行了内弹道装药优化设计,得出了较为理想的优化设计结果,证明了复合形法用于内弹道优化的合理性、可行性。本文工作得出的结果对迫榴炮的研制与改进具有一定的指导意义。
