多EFP拦截整体设计及多角度下交汇概率计算
2018-07-31史庆杰池朋飞
史庆杰,曹 兵,池朋飞
(南京理工大学 机械工程学院, 南京 210094)
随着近年来精确制导弹药技术的发展,越来越多的重要军事目标受到威胁,如重要军事设施、大型军事舰艇等。为实现对各种精确制导弹药等现代化来袭目标的高效拦截,给作战防御系统提出了更高战术技术要求。
为了提高重要军事目标的生存能力,就必须加大对拦截武器系统的进一步研究,各个国家在武器拦截方面都做出了极为深度的研究。不论是远距离拦截还是近距离防御都是需要研究的课题,利用爆炸成型弹丸的特点设计多爆炸成型弹丸(EFP)拦截结构能够有效阻止来袭目标的破坏。多爆炸成型弹丸能够产生多个毁伤元,形成一个拦截弹幕,可以有效击毁来袭目标,成为近距离防御的杀手锏。
本文设计的拦截弹面共布置了间距40 mm的200个EFP弹丸,形成一个圆形的拦截弹幕,拦截一定高度的来袭导弹,来袭导弹和拦截弹幕形成一个交汇的投影面积,通过编写交汇程序计算拦截概率。由于来袭导弹具有角度不确定性,本文计算了导弹侵入角0°~90°间隔10°变化的交汇概率以及在拦截系统的随动误差下对交汇概率的影响。
1 单个EFP结构及拦截整体结构
1.1 单个EFP结构
拦截弹面上布置的200个EFP装药采用圆柱形装药。结构如下(图1):
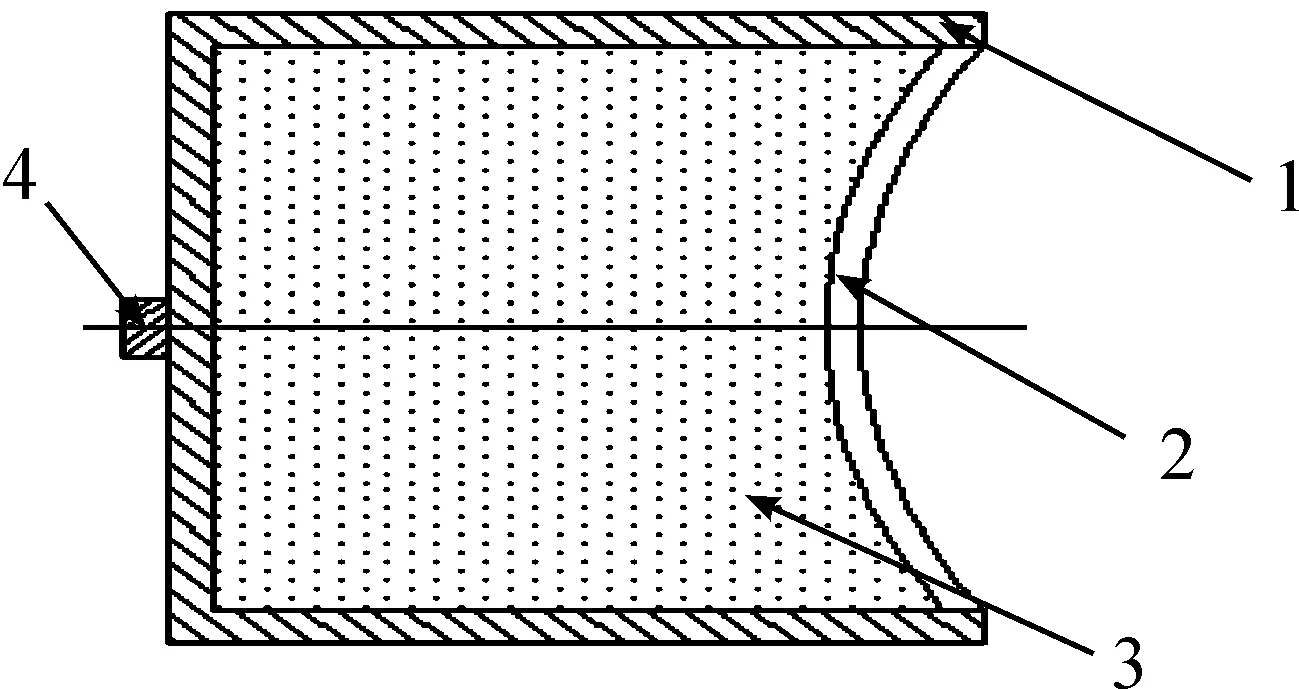
1.壳体; 2.药型罩; 3.炸药; 4.传爆药柱
EFP速度经验关系式:影响EFP速度的主要因素有装药的种类、装药的形式、药型罩的材料和厚度,通常采用试验方法研究,在试验基础上获得的经验关系式为
其中,η=(16/17)(ρelp/ρmζ);lp为药型罩中心点处装药厚度;ζ为药型罩厚度;ρe为装药密度;ρm为药型罩的材料密度。
1.2 拦截系统整体结构模型
由于来袭目标的方向不确定性,这就要求拦截系统具有各个方向的机动性,不仅要在一定角度内做俯仰运动,而且还要能够在圆周方向360°旋转。利用SolidWorks软件进行装配建模,整体结构示意图如图2。
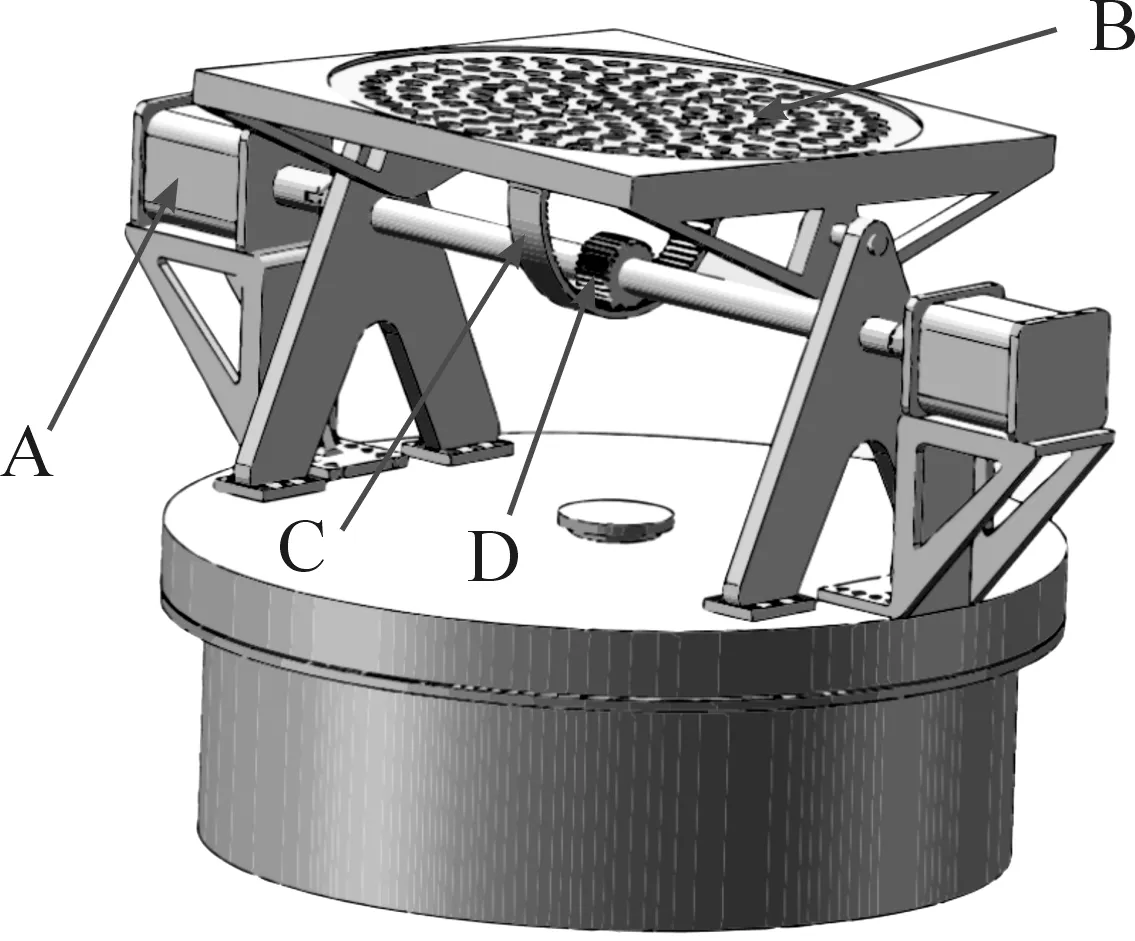
A.步进电机; B.装药平面; C.弧形齿条; D.齿轮
整个拦截系统分成上下两部,上部通过螺栓固定在下部的旋转圆盘上,两侧的步进电机在支架的支撑下也固定在旋转圆盘上,上部机构所形成的俯仰运动主要通过两侧的步进电机带动传动轴,传动轴上的D齿轮投影弧形齿条C啮合,在电机的带动下控制载弹圆盘的运动,最终实现拦截系统的俯仰运动,如图3到图4。
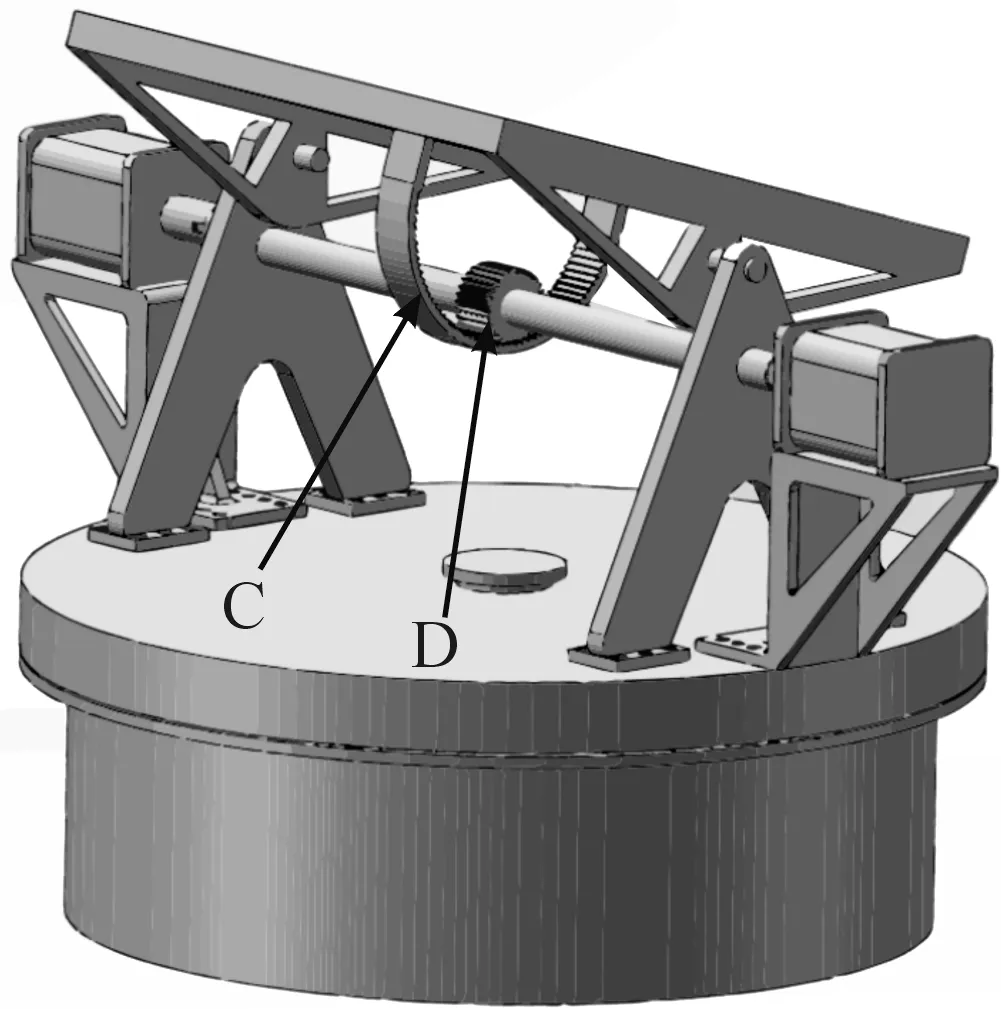
图3 载弹圆盘的俯仰运动一
图4 载弹圆盘的俯仰运动二
拦截系统的下部为一旋转底盘,旋转底盘的运动主要是靠内部的电机带动齿轮a与内齿轮和齿轮b啮合,通过旋转轴带动圆盘转动,实现圆周方向360°运动,如图5到图6,下半部分结构示意图如图7。
1.3 拦截系统形成弹幕拦截
当来袭目标进入拦截范围以后,拦截系统接受指令发射拦截弹丸形成一个圆形拦截弹幕,由于属于近距离防御,所以必须击中来袭导弹的战斗部确保其丧失毁伤能力。拦截系统形成拦截弹幕拦截导弹示意图如图8。
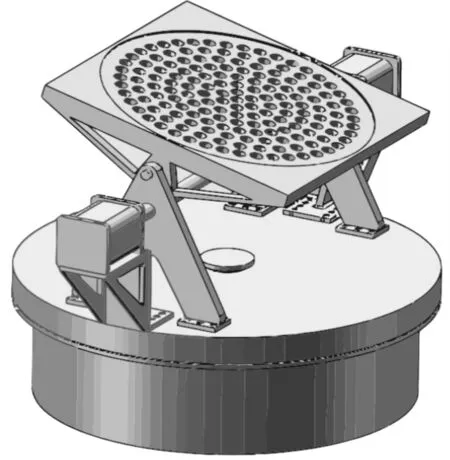
图5 底盘圆周转动运动方向一
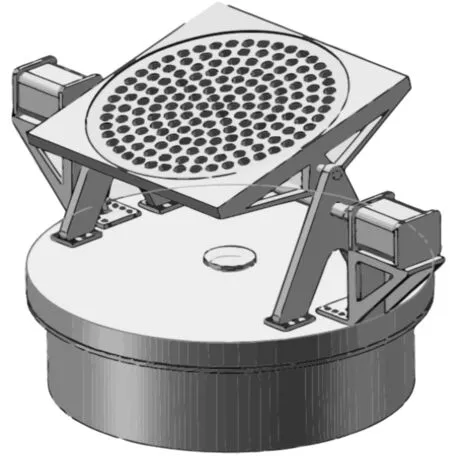
图6 底盘圆周转动运动方向二
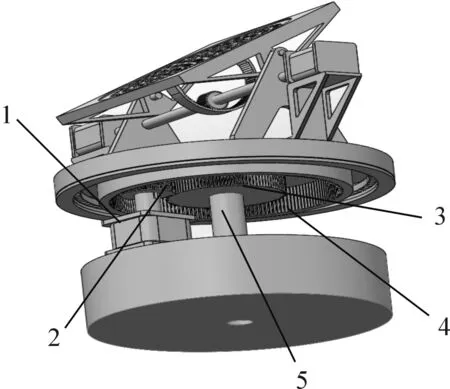
1.步进电机; 2.齿轮a; 3.齿轮b; 4.内齿轮; 5.旋转轴
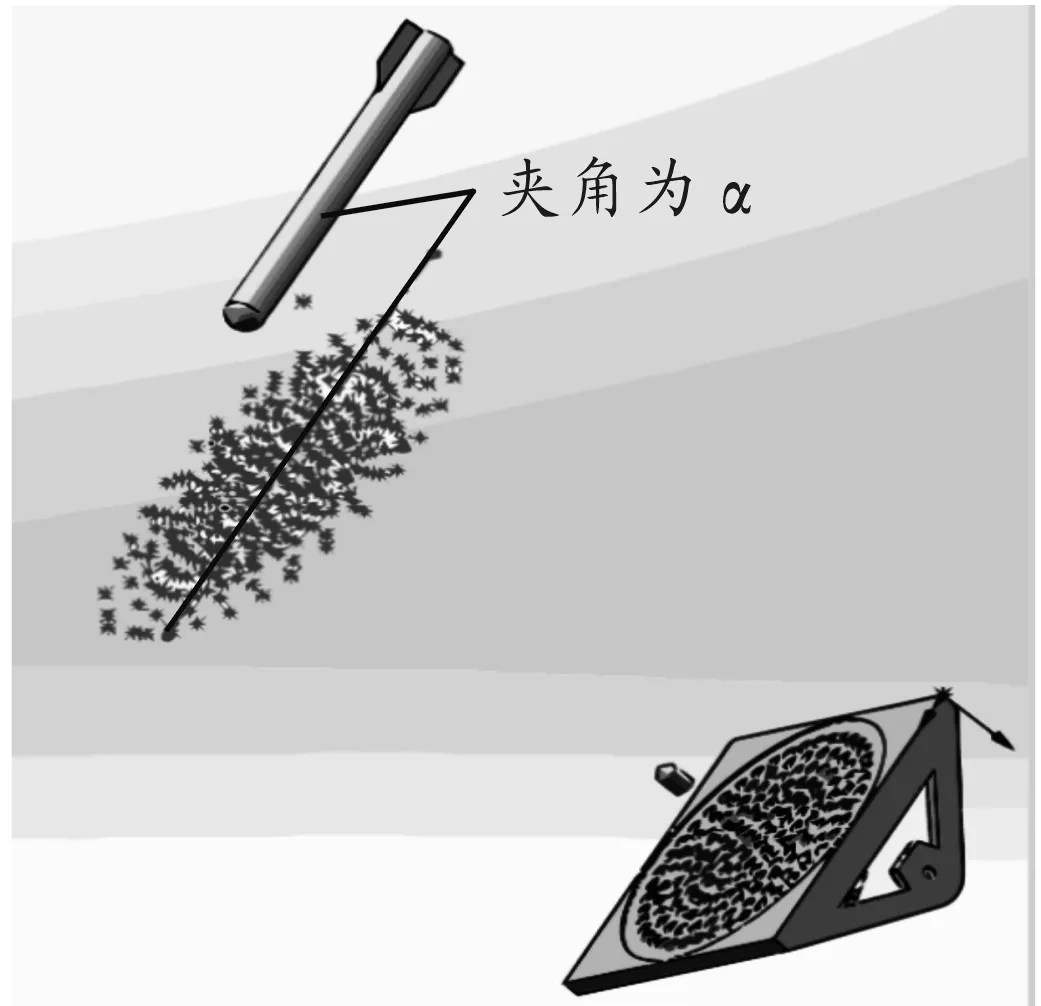
图8 拦截弹幕拦截示意图
2 多角度下交汇概率计算
2.1 交汇概率计算原理
来袭导弹与拦截弹幕在同一平面内形成投影面积,在一定高度上拦截弹丸在相对应的散布面积内随机分布,此时来袭目标的位置也随机出现在该散布面积内,本文研究的条件为拦截指定高度,进入拦截区域1 m的来袭导弹,导弹总长不考虑,程序每运行一次,统计在来袭导弹的投影面积中的弹丸点数,汇总成表。不同角度的来袭目标在散布面积内的投影面积有所变化,本文研究了在无误差及0.1°~0.3°系统的随动误差内分别计算了α为0°、10°、20°、30°、40°、50°、60°、70°、80°以及90°的交汇概率。在随动误差的影响下,导弹进入长度发生偏移,从而导致在拦截平面上的投影面积发生改变,导弹进入拦截区域长度变化如表1所示。
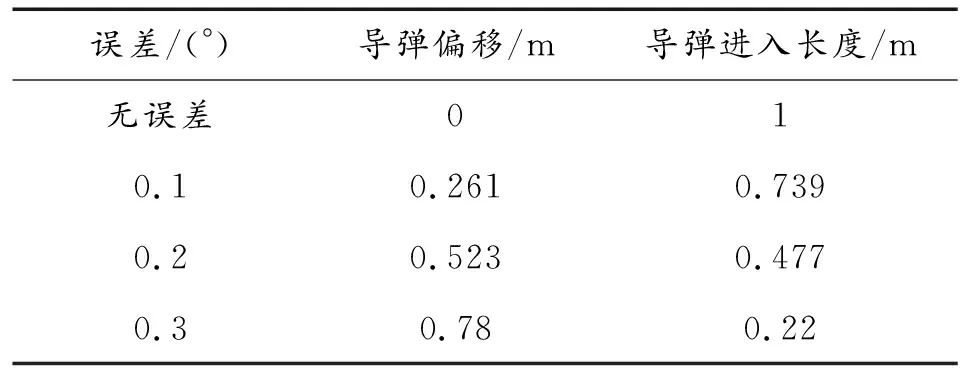
表1 0.1°~0.3°误差下导弹长度变化
在散布面积内每种角度下做了100次随机分布的交汇仿真试验共计1 000次。本文仅考虑来袭导弹进入拦截弹幕的最前部分与弹丸交汇情况,某次典型交汇程序运行如图9所示。
图9 某次典型交汇程序运行图
2.2 交汇概率计算结果及分析
本文考虑了随动误差为0.1°、0.2°、0.3°及无误差带来的拦截概率影响,拦截系统的随动误差直接影响拦截弹幕相对于来袭导弹的偏移,从而导致来袭导弹进入拦截范围的长度变化以及投影面积的改变,影响交汇概率。图10和图11显示了无误差以及0.1°~0.3°误差条件下随交汇角度的变化,交汇概率以及交汇时击中来袭目标弹数的变化趋势。
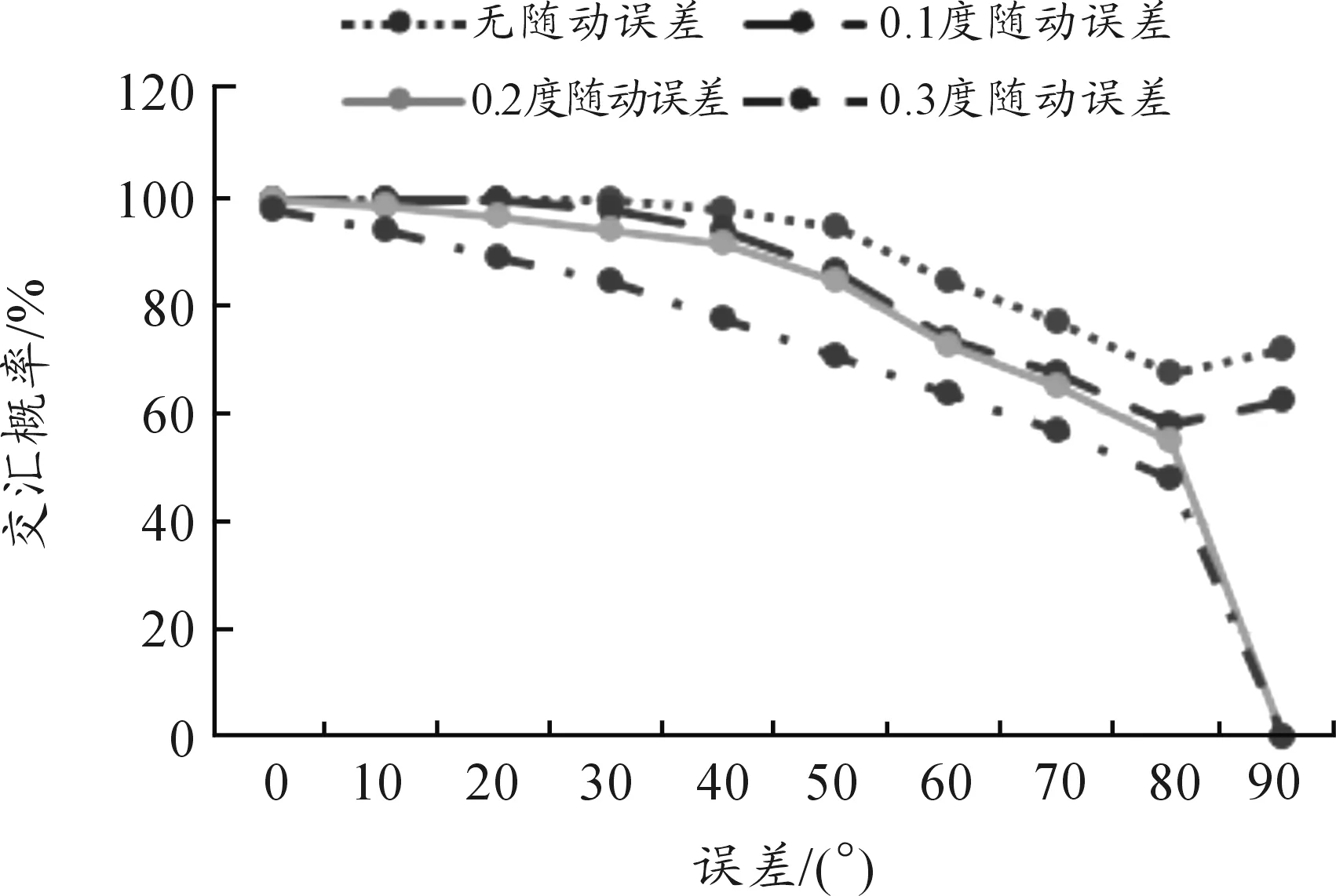
图10 不同角度下随动误差对交汇概率的影响
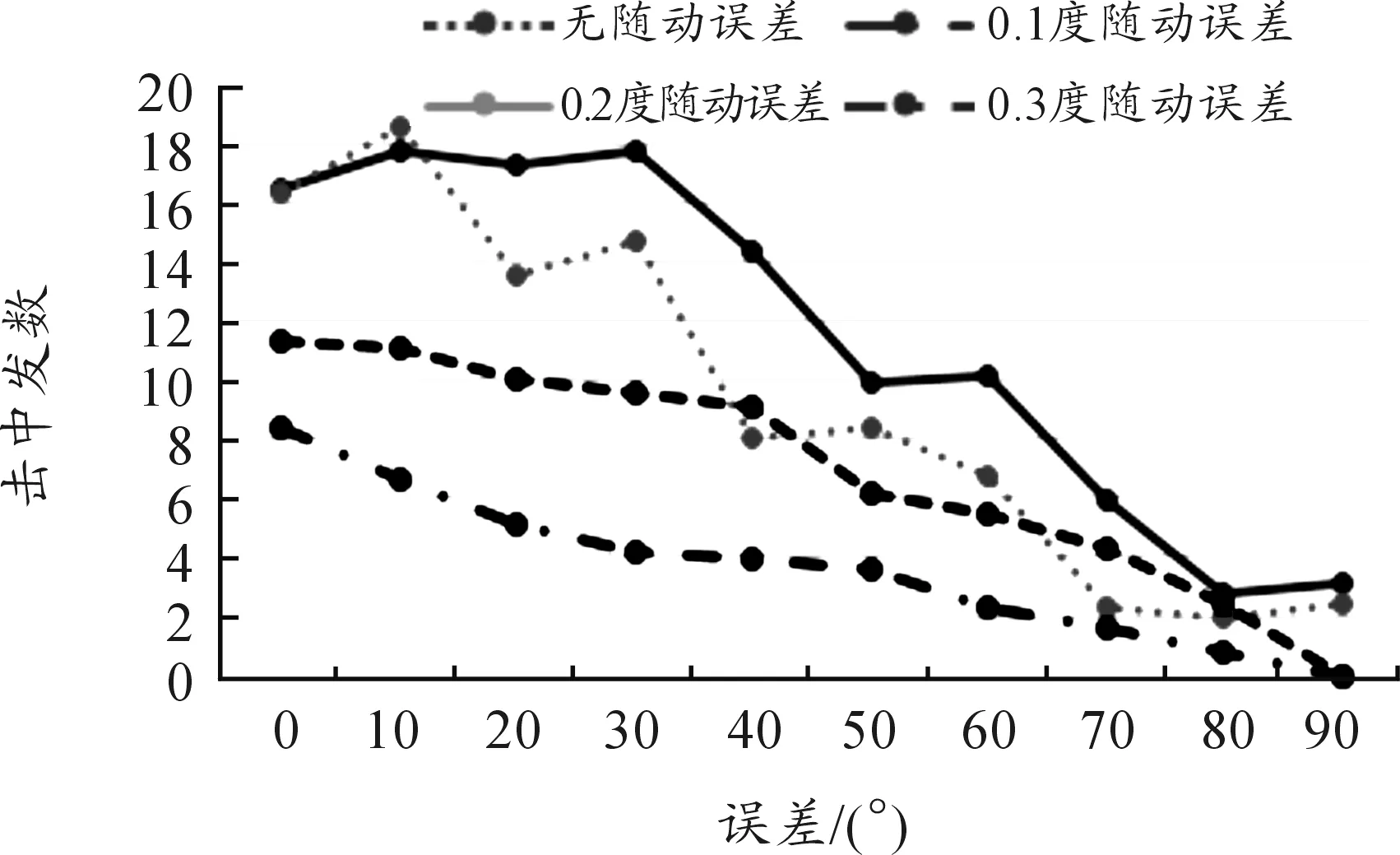
图11 不同角度下随动误差对击中发数的影响
3 结论
1) 随着交汇角度α从0°变化到90°过程中,交汇概率整体呈下降趋势,击中发数也随着交汇角度的增加而降低。
2) 在0.3°的随动误差中交汇概率下降最为急剧,当交汇角度到达90°时,即来袭目标与拦截方向垂直时,理论交汇概率为0,因为此时误差导致的偏移量已经超出拦截范围。
3) 由表1和表2可知,当随动误差不超过0.2°时且交汇角度在0°~50°范围内的拦截交汇概率至少为71%,此时至少3发拦截弹丸击中目标,拦截交汇概率和击中发数均为最佳。
