基于表面织构的高超声速飞行器舵翼热防护技术研究
2018-07-31常秋英蔡礼港段晓亮
常秋英,蔡礼港,杨 超,段晓亮
(1.北京交通大学 机械与电子控制工程学院, 北京 100044;2.中国兵器工业导航与控制技术研究所, 北京 100089)
飞行器以高超声速飞行时,由于激波压缩、粘性摩擦等作用,高温空气不断向壁面传热,会导致壁面温度快速升高,存在气动加热现象[1]。飞行器温度过高会影响内部器件的正常工作,甚至会导致表面材料变形、烧蚀等。对飞行器的控制面而言,由于其前缘尖锐且厚度一般较薄,飞行时需经受在高马赫气流下严酷的气动加热环境,承受极大的气动力载荷和操纵机构的机械载荷,还要在极高温度下保持其外形和刚度,因此控制面的热防护是影响高超声速飞行器设计成败的关键[2]。目前热防护系统可分为被动式、半被动式和主动式[3]。由于控制面的热容量有限且难以布置主动式热防护系统,同时又有保持外形不变的要求,不能采用半被动式热防护系统[4]。因此控制面一般采取被动式热防护系统,使用耐高温材料制成,并在表面涂覆热防护涂层[5-6]。与航天器不同,高超声速火箭弹作为军事上用于集群打击的单次消耗品,首先要求其维修保养简单、采购方便,其次要求造价适宜、制造工艺成熟、适合量产[7]。而目前热防护涂层仍存在制备工艺繁琐、涂层的高温结合能力不足等问题[8],因此,仍要寻求一种适合高超声速火箭弹控制面(舵翼)的符合工程应用实际的热防护方案。
表面织构(Surface Texture)是指借助一定的加工设备和手段在物体表面生成一系列具有一定分布规律和尺寸的微小结构,用以改善表面的摩擦学或其他方面的性能[9]。表面织构作为一种减小摩擦、磨损的有效手段已被得到广泛认可和应用,如在轴承和机械密封等处于流体润滑状态的部件,可产生附加的动压效应提高表面承载能力[10-11]。近年来,表面织构的应用范畴也被逐渐推广到其他领域和学科,沟槽型表面织构以其显著的减阻效果与良好的工程应用前景而备受关注,试验结果表明合理设计的沟槽可以显著降低亚音速飞行器的壁面摩擦阻力[12],也有学者对鲨鱼皮[13]和鸟类羽毛表面[14]沟槽结构的减阻性能进行研究。
气动加热的热源主要来自空气的剧烈压缩和粘性摩擦,沟槽型表面织构既然能够降低飞行阻力,能否降低高速气流的粘性摩擦,进而在一定程度内降低舵翼表面的温度?目前表面织构在高超声速工况下的研究仍少见报道。为研究沟槽型表面织构在高超声速飞行器上的热防护效果,基于某型号高超声速火箭弹,在其舵翼表面添加三角形沟槽表面织构,使用有限元方法对其进行数值仿真,以此探究沟槽对舵翼表面温度分布的影响。
1 仿真模型
1.1 控制方程
飞行器在高超声速飞行时,在近壁面形成附面层,由粘性力产生的气动热就是通过附面层传入飞行器结构内部的。研究气动加热的情况需要求解边界层内气动流动状态的基本方程。气体边界层方程是由Navier-Stokes方程、气体状态方程以及湍流补充方程构成的方程组。在不考虑体积力和外部热源,直角坐标系下的三维非定常可压N-S方程是连续性方程、能量方程、气体状态方程,可表示为:
(1)
式中,x,y,z分别为三个直角坐标方向变量,t为时间变量,Q为流场守恒变量,Ec,Fc,Gc分别为三个坐标方向上的无粘对流通量,Ev,Fv,Gv分别为三个坐标方向上的粘性耗散通量,其具体表达式详见文献[15]。
理想气体状态方程
ρ=ρRT
(2)
对于动力粘度的计算,当考虑湍流时,使用湍流粘性系数来模拟,粘性系数为:
μ=μl+μt
(3)
其中μl为层流粘度,由Sutherland公式近似给出:
(4)
式中:μ0为粘性系数,T为环境温度,TS为苏士南常数,TC=273.16 K。
而μt为湍流粘度,由湍流模型给出。湍流模型采用Spalart-Allmaras湍流模型:
(5)
Spalart-Allmaras模型是单方程模型,主要用于求解有关涡粘性的运输方程。利用雷诺类推概念,湍流传质和传热模型如下:
(6)
式中:(τij)eff为粘性发热项。建立模型时作以下基本假设:(1) 材料的热物性参数,如导热系数、定压比热容、密度取为常数;(2) 舵翼材料为钛合金,视为各向同性,其导热系数为15.1 W/(m·K),比热容取为650 J/(kg·K);(3) 无内部热源。采用有限体积法求解以上方程,无粘通量采用Roe的FDS格式,捕捉激波算法采用TVD格式,粘性通量采用二阶中心差分格式,时间推进采用LU-SGS隐式方法。
1.2 网格划分
根据实际舵翼尺寸,建立了舵翼的三维模型,如图1所示。使用Gambit对舵翼与计算域划分非结构网格,来流空气从图1(a)中自左向右流动。。所建立的计算域如图2所示。
根据舵翼实际尺寸,建立舵翼的三维模型,如图1。随后建立计算域并划分非结构网格,计算域的尺寸为2 200 mm×840 mm×840 mm,舵翼前缘距计算域进口距离为770 mm,如图2所示,所划分的网格质量均大于0.2。
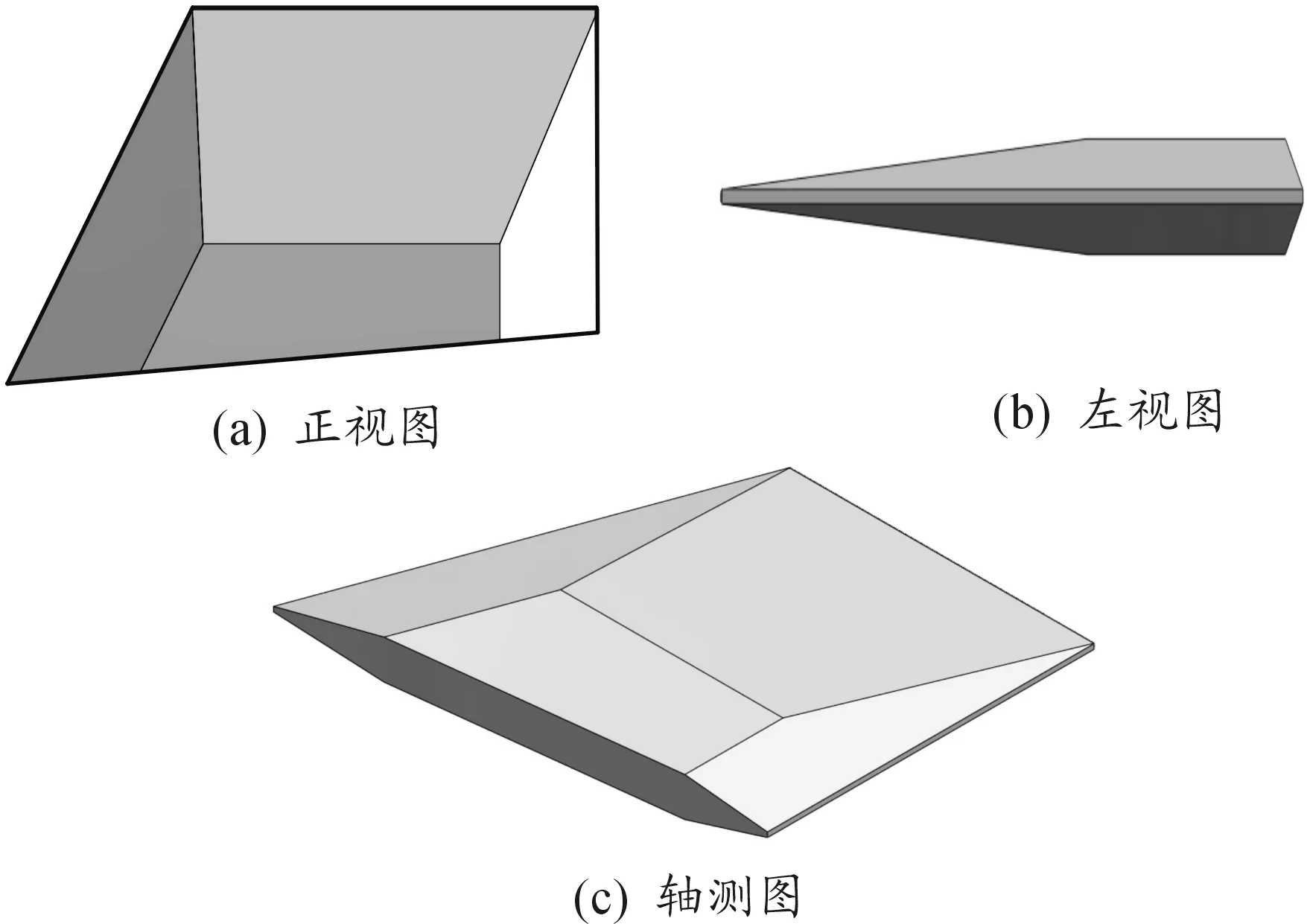
图1 舵翼立体图

图2 计算域
为使舵翼与流场网格的过渡合理,节省计算资源同时保证计算精度,需要控制网格的生成过程与分布规律,建立舵翼表面以及整个流场的网格分布模型。计算域中贴近壁面的区域各项物理参数变化较大,设置了附面层网格。沟槽的截面形状为等腰直角三角形,其斜边边长为1或2 mm。通过控制沟槽附近网格的节点分布,达到网格加密效果。沟槽附近网格划分情况如图3。
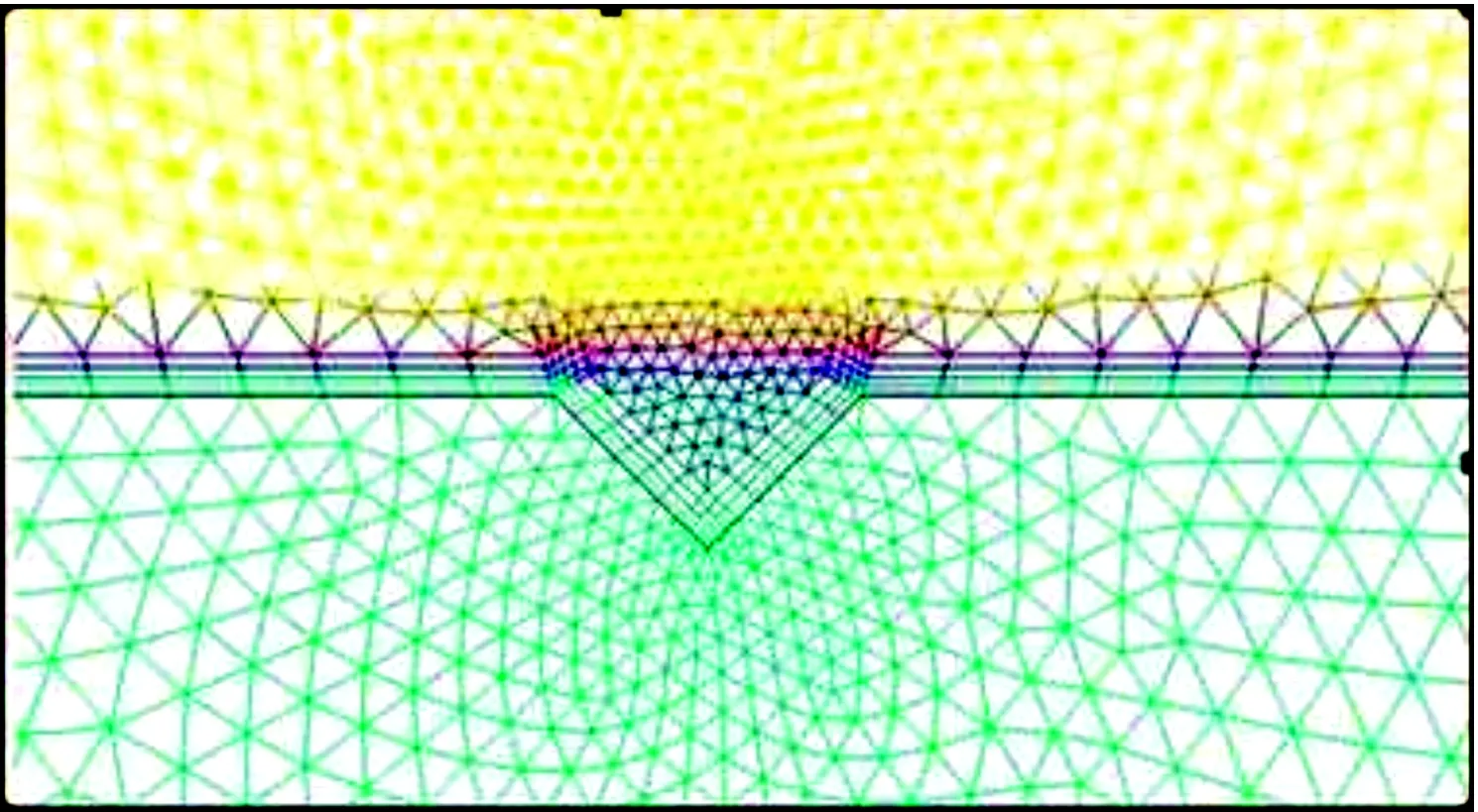
图3 三角形沟槽网格剖视图
综合考虑飞行器的实际飞行工况,使用FLUENT进行数值模拟,设置来流参数为海拔20 km处,大气温度为216.65 K,大气压力5529 Pa,大气密度为8.891×10-2kg/m3,大气动力粘度为1.421×10-5N·s/m2,热传导率为1.953×10-2W/(m·K),舵翼以6马赫速度飞行30 s。
2 仿真结果分析
2.1 无表面织构舵翼仿真结果分析
为定量分析舵翼表面温度,在舵翼表面取四个温度检测点,温度监测点的位置和编号如图4所示。舵翼表面的平均温度为933 K,4个检测点的温度变化情况如图5所示,其中上尖点(1)和下尖点(2)的最高温度分别为1 276.5 K和 1 263.8 K。舵翼前缘温度已经超出一般金属的温度耐受范围,而舵翼主体温度保持在900 K左右。
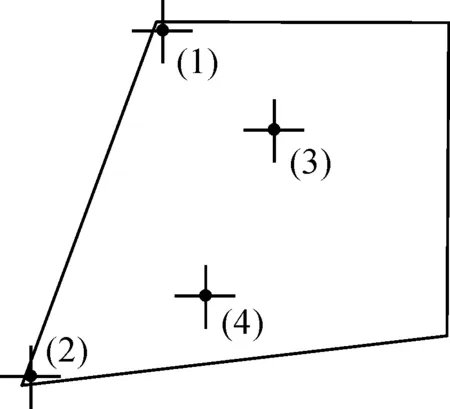
图4 舵翼表面4个监测点位置
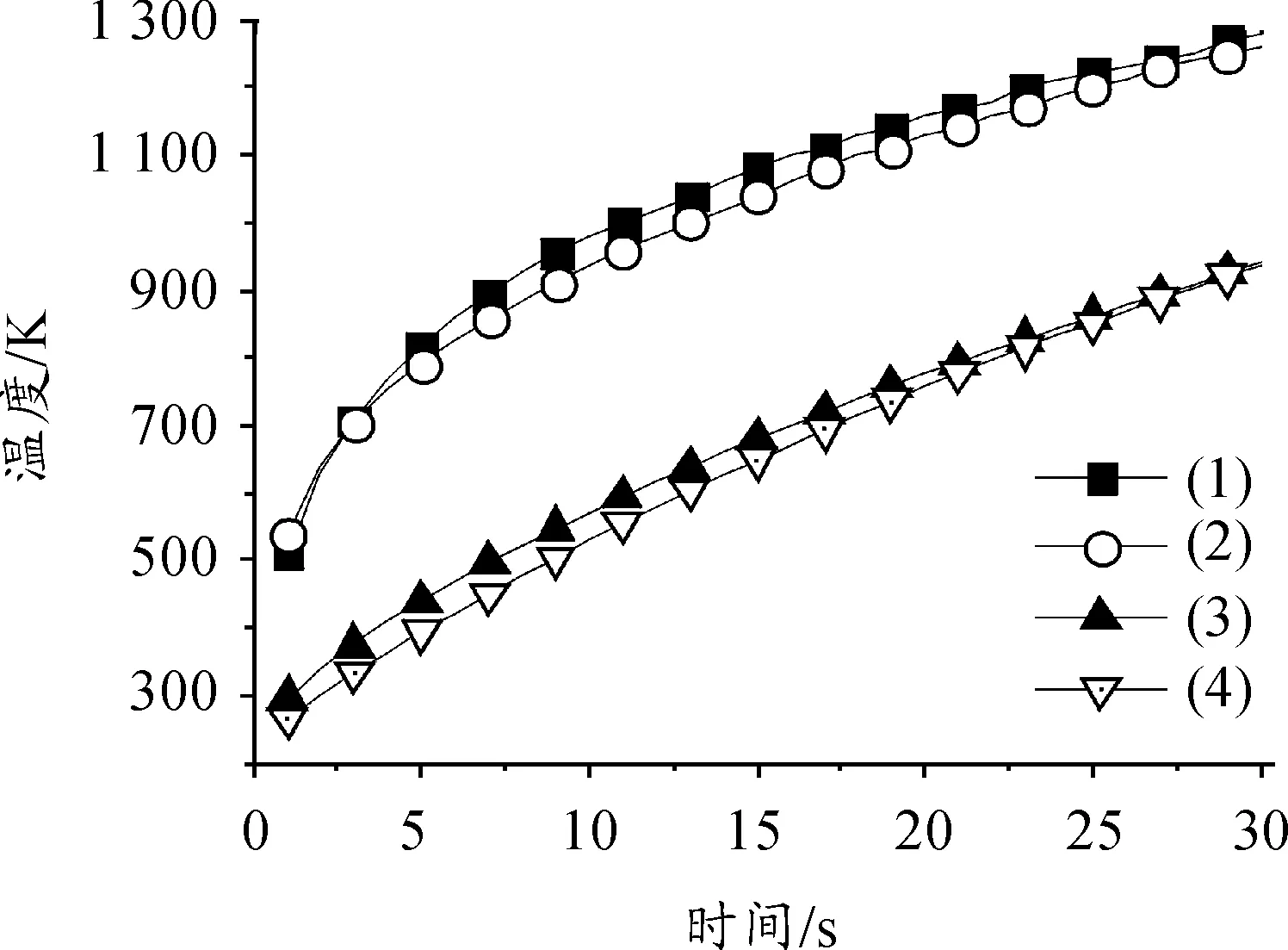
图5 无表织构舵翼4监测点温度变化情况
2.2 不同方向沟槽仿真结果
先探究横向、斜向(与来流方向夹角为45°)和纵向(顺流向)沟槽对舵翼温度分布的影响。选择在舵翼中间区域添加沟槽,所添加的沟槽在舵翼表面的分布如图6所示。
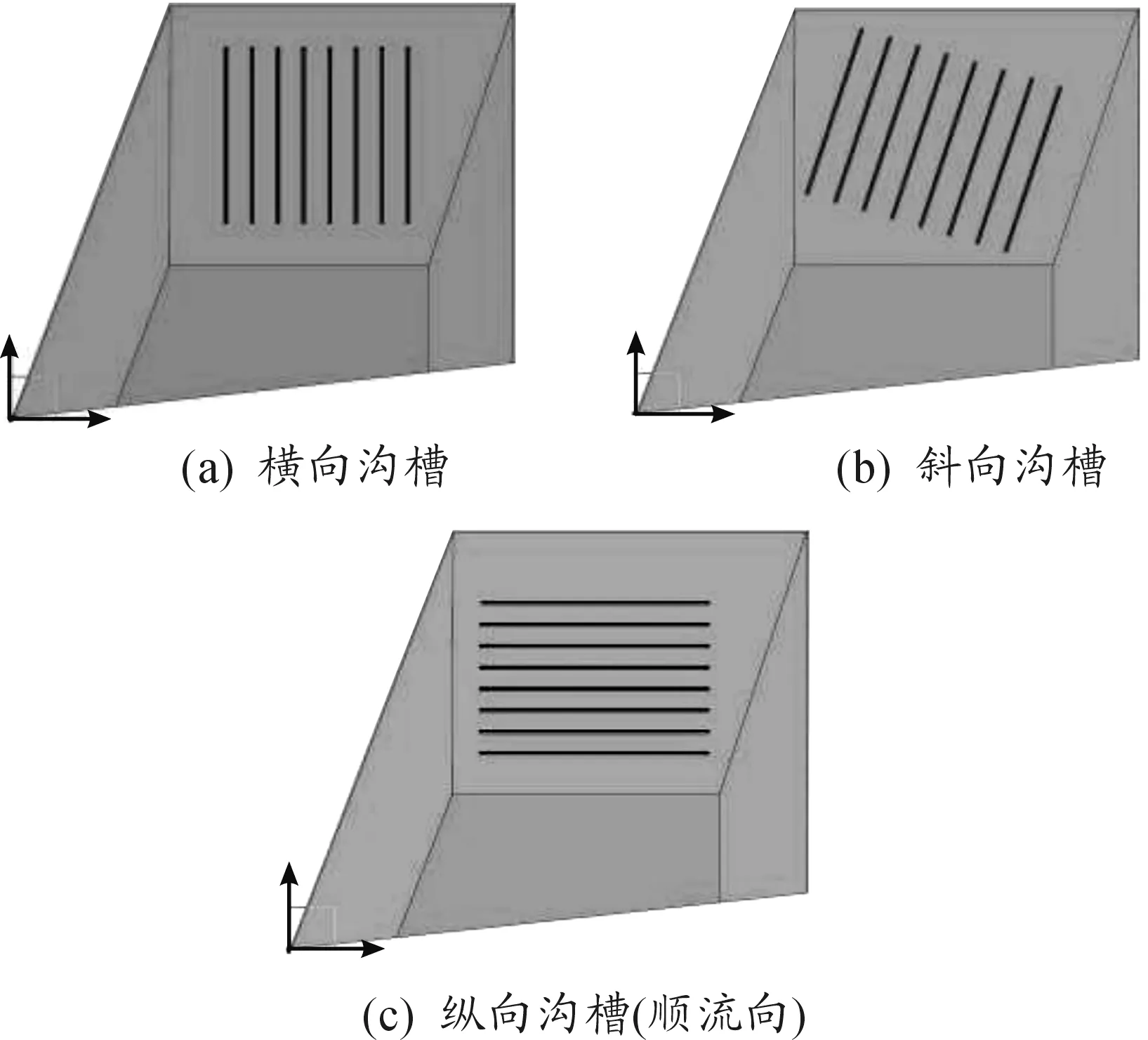
图6 舵翼表面添加不同方向的沟槽型表面织构
所添加的横向、斜向和纵向沟槽的舵翼表面平均温度和前缘最高温度如表1,只有纵向沟槽降低了舵翼的平均温度和前缘最高温度。为分析表面沟槽的温度分布情况,沿来流方向截取舵翼剖面,如图7所示。
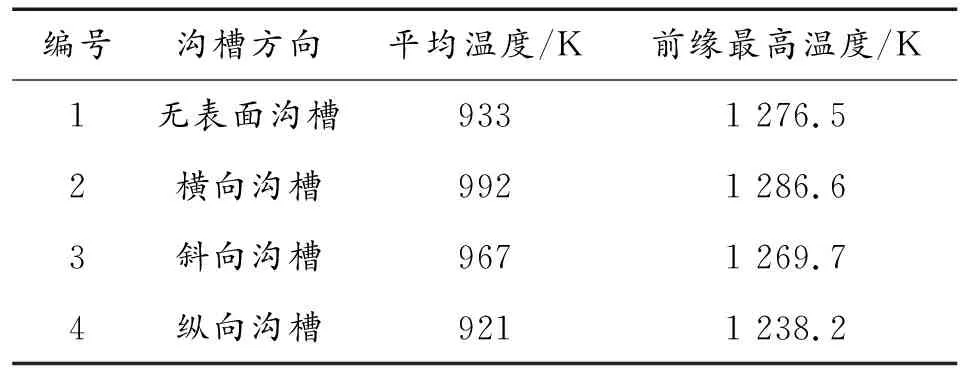
表1 不同方向沟槽仿真结果
对于纵向沟槽,在起始位置形成局部高温区域,随着流动状况的改变,纵向沟槽的下游区域不存在局部高温区。纵向沟槽降低了舵翼表面平均温度和前缘温度,可以将其设置为贯通形式,避免热量在沟槽的起始位置聚集。
对于横向和斜向沟槽,热量集中在沟槽内部不能很好地发散出去,横向沟槽的截面速度分布如图8。沟槽内部壁面的气流流动速度明显降低,气流在横向沟槽内部形成微漩涡,其本身产生的涡能如同空气轴承一样起到降低摩擦阻力的作用[16]。但是在高超声速的状况下,这种微旋涡结构会导致高温空气在沟槽内难以发散,形成局部高温区域。
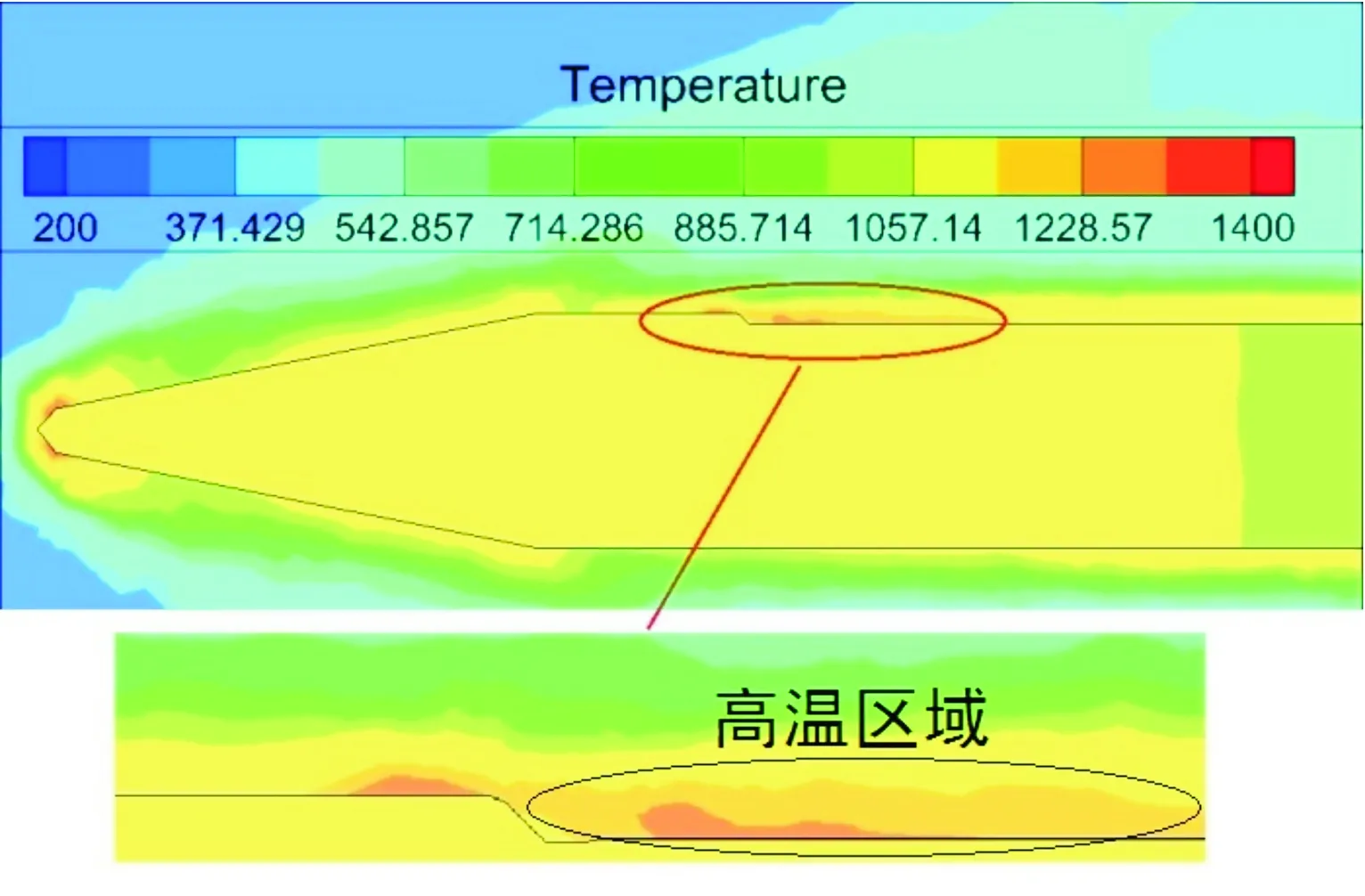
图7 纵向沟槽剖面的温度分布彩色印刷
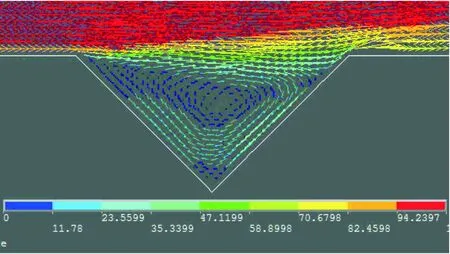
图8 横向沟槽剖面流动速度分布彩色印刷
2.3 纵向贯通沟槽降温效果优化
沟槽的数量与尺寸会影响舵翼表面的温度分布。为探究纵向贯通状沟槽的最佳降温效果,分别改变纵向贯通沟槽的数目与宽度,如表2所示,图9给出表2中第3组和第4组的沟槽形貌。

表2 不同纵向贯通沟槽的平均温度
图9 贯通的纵向沟槽形貌
表2中各类型沟槽对应的监控点温度变化情况如图10所示。纵向贯通沟槽对各监控点均有降低温度的效果。各个监测点温度的下降程度不同,其中上下尖点监测点的温度下降较明显。仿真中最低温度为1220 K和1210 K,最大的降温值为55.8 K和53.4 K,均出现在第四组。而在舵翼内部,3号和4号监测点降温幅度较小。结合图10和表2可以看出,降温结果最好的是第4组。
3 结论
1) 舵翼前缘处温度最高,是气动热现象发生的重要部位,随着位置的向后推移,温度逐渐降低。
2) 在横向和斜向沟槽内会产生微涡旋,存在局部高温区域,在舵翼表面布置纵向贯通的沟槽能够得到较好的降温效果。
3) 本研究中纵向贯通沟槽型表面织构获得最好降温效果的参数为:条数8以及宽度1 mm,其中舵翼前缘尖点的最佳降温幅度约为50 K,而舵翼内部降温幅度不大,舵翼的平均温度从933 K降低到909 K,温度降低率为2.57%。
4)通过对高超声速火箭弹舵翼进行建模以及数值模拟,发现纵向贯通的沟槽型表面织构具备一定的降温效果,但仍需进一步优化和验证。
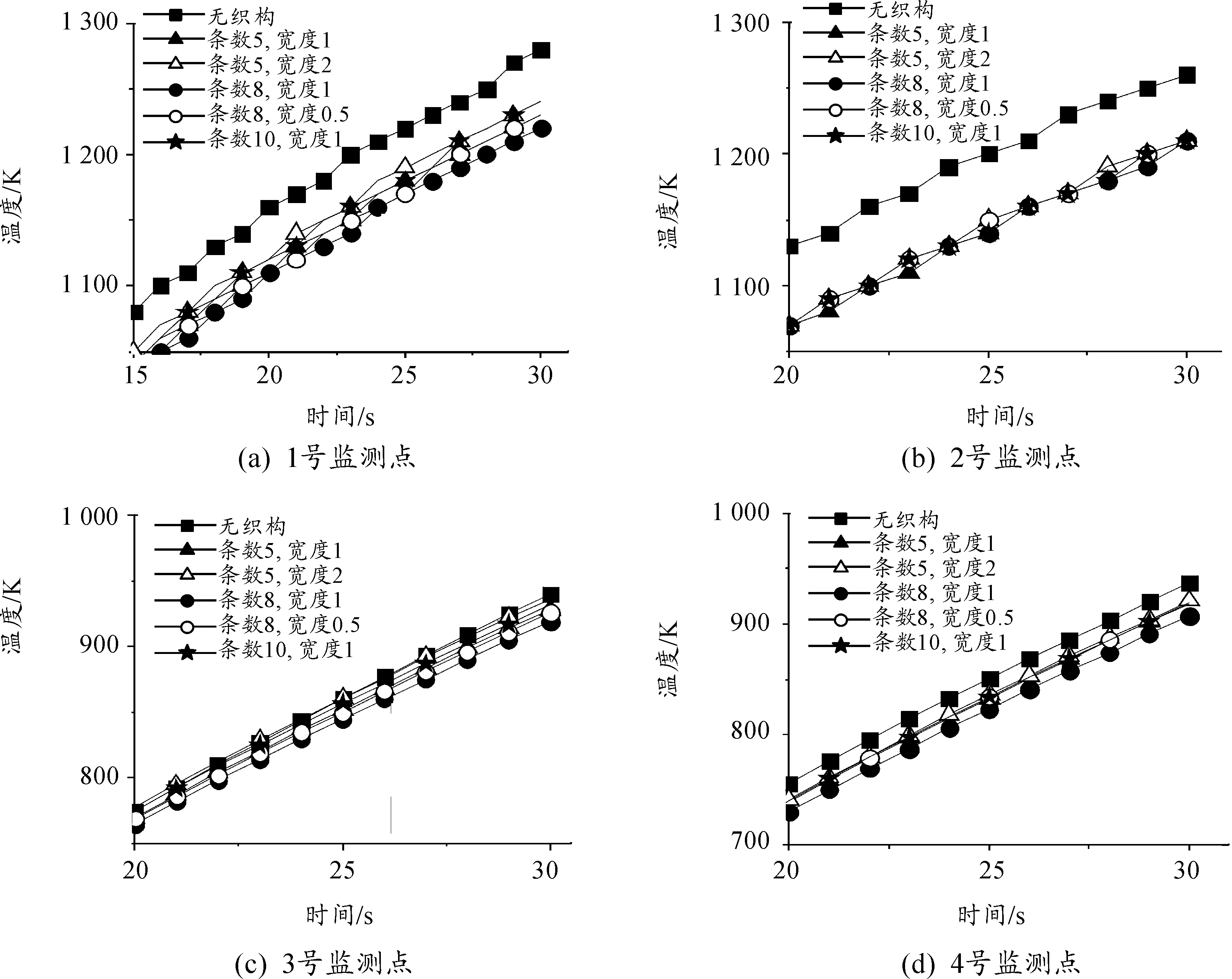
图10 系列沟槽监测点温度变化情况
