一种混合路径规划方法在装甲车辆CGF中的应用

邓 青，薛 青，陈 琳，陈 俊

(1.陆军装甲兵学院， 北京 100072； 2．陆军指挥学院，南京 210045)

装甲车辆计算机生成兵力(Computer Generated Forces,CGF)面临的虚拟战场环境异常复杂，包含了真实战场环境的大部分要素[1]，例如地形地貌、道路、建筑、水系、植被、障碍物、弹坑等等。规划约束条件多，并且战场环境具有不确定性，例如某一时刻，装甲车辆CGF在沿着规划好的路径行进时，前方出现了新的弹坑，构成车辆前进的障碍，为避开障碍物就需要重新进行路径规划。目前常用的路径规划方法有图搜索算法、遗传算法、人工势场法、快速扩展随机树法[2-5]，但也存在一些不足，比如搜索空间大、局部寻优能力不强、搜索速度慢、实时性能力不足等。基于此，结合分层[6]思想，本文提出一种混合路径规划方法，将装甲车辆CGF路径规划分为全局路径规划层和局部路径规划层，运用IGA和几何算法搜寻路径，通过仿真实验验证该方法具有全局搜索和快速灵活的特点，能够达到仿真的实时性要求。

1 规划空间模型

规划空间建模就是运用环境表示方法，将虚拟战场环境中与路径规划有关的要素由其原始形式转化为适合规划的内部模型，从而量化成可通行与不可通行区域。规划空间建模是路径规划的前提。

可视图法以多边形障碍物模型[7]为基础，将路径规划问题转化为路径点组合寻优问题。其具体构造过程：任意形状障碍物用多边形近似代替，用线段将装甲车辆CGF的起始点s和障碍物的顶点以及目标点g连接，并要求起始点和障碍物各顶点之间、目标点和障碍物各顶点之间以及各障碍物顶点与顶点之间的连线均不能穿越障碍物，对虚拟战场环境中的所有顶点都执行完这个操作后，就得到了该环境的可视图，如图1所示。

用可视图法建立规划空间模型后，装甲车辆CGF的路径可由起始点、路径点、目标点构成，其中路径点用障碍物的顶点来表示。如图1中，节点序列{s,A,B,g}用来表示一条路径，s为起始点，A、B为路径点，g为目标点。

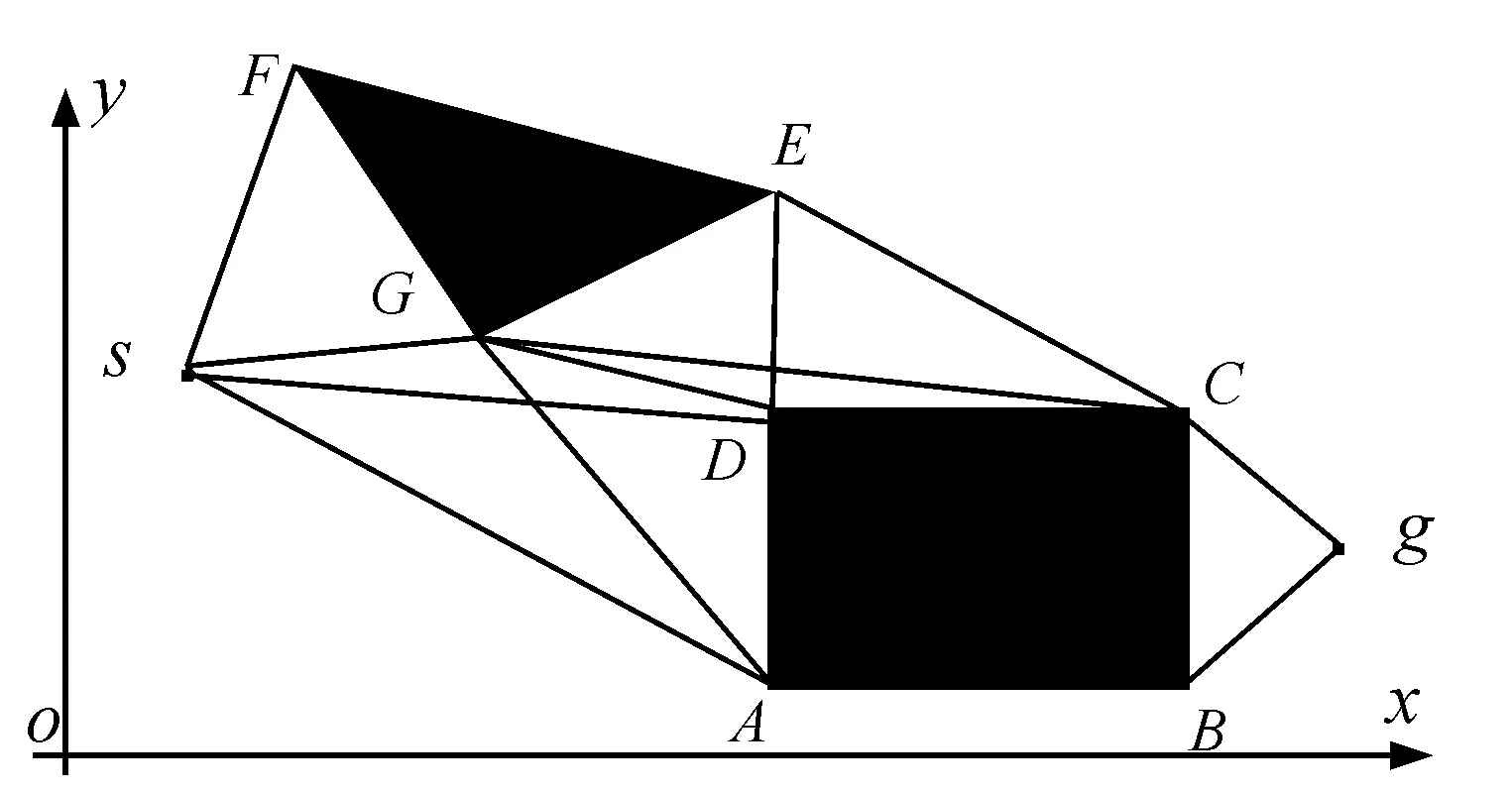
图1 可视图

2 混合路径规划方法

基本思想是在完成路径规划预处理后，将轮式装甲车辆CGF路径规划分为两层：全局路径规划层和局部路径规划层。其中，全局路径规划层主要用于仿真前生成初始全局路径，采用的算法具有全局搜索性能；局部路径规划层是在初始全局路径的基础上，主要用于仿真中实时避开一些视界内或者车辆所能探测范围内新出现的障碍物，规划算法的效率越高越好。

2.1 基于IGA的全局路径规划

装甲车辆CGF全局路径规划需要完成大部分路径规划的计算工作，搜索算法要求具有较强的搜索能力。免疫遗传算法(Immune Genetic Algorithm,IGA)具有遗传算法的全局性和免疫算法的自我调节功能[8-9]，提高传统遗传算法的总体搜索能力，最终找到最优解。介于IGA的优势，将其用于全局路径规划，重点研究抗体编码、适应度、选择算子。

本文中的抗体编码采用符号编码，对所有顶点按横坐标值从小到大进行排序确定顶点编号(v1,v2,…,vn)，用这些编号来表示路径点，则装甲车辆CGF的路径表示可简化为一维编码，具有编码长度短、简单直观的优点。

装甲车辆CGF路径的适应度主要考虑路径长度和路径偏离起始点目标点连线sg的距离，采用各项评价函数相乘的形式确定适应度函数。根据规划空间模型，可求路径长度适应度为：

(1)

式(1)中，n表示路径中包含的顶点数量；d表示起始点至目标点的距离；dij表示两路径点的距离。

路径偏离适应度为：

(2)

由式(1)、(2)得到适应度为：

fit=fit1×fit2

(3)

选择是模仿自然选择现象，目的在于把优化的抗体直接遗传到下一代或通过配对交叉产生新的抗体再遗传到下一代。选择算子采用比例选择算子，其基本思想建立在群体中抗体的适应度和浓度的评价基础上，各个抗体被选中的概率P与其适应度大小成正比，而与浓度大小成反比，表示如下：

(4)

2.2 基于几何算法的局部路径规划

当装甲车辆CGF按照初始规划的全局路径机动，如果虚拟战场环境出现了新的障碍物，基于两点之间直线距离最短的思想，首先会判断这个障碍物是否在当前行进方向上，如果没有在当前行进方向上，则直接按照预先规划路径行进，不用考虑该障碍物；如果在当前行进方向上，则要分析怎样绕过这个障碍物，即选择一个可行路径点避开障碍物。这是局部路径规划的内容。为便于描述，给出以下几个定义：

定义1：装甲车辆CGF的当前位置为r，下一个子目标点为g，其中g为初始全局路径中r的下一个路径点，则rg连线的方向称为装甲车辆CGF的目标方向。

定义2：装甲车辆CGF的运动方向与目标方向之间的夹角称为路径方向角，记作δ。

本文提出几何算法的基本思路如下：如图2所示，以装甲车辆CGF的当前位置r为原点，以目标方向rg为横轴建立相对坐标系x′o′y′，则相对坐标系的横轴将障碍物顶点分为上、下两个集合，考虑视觉局限性，选择CGF当前位置r所能观察到的障碍物顶点A、F、E、D作为备选路径点，求取并比较上、下两个顶点集中备选路径点的路径方向角，分别找到上、下两个顶点集中路径方向角最大的两个点A、D，然后选择这两个点中路径方向角较小的点A作为“最佳路径点”行进。具体流程见图3。

3 实验验证

3.1 算法对比分析

为了验证本文提出的混合路径规范算法的性能，选择遗传算法和A*算法进行对比实验。算法参数设置如下：遗传算法的种群大小为150，交叉概率、变异概率分别取0.8、0.1，终止进化代数为200；A*算法的启发函数h(n)代表从当前节点到目标点的估计路径长度。选择算法的运行时间、路径长度两个指标来评价算法优劣。为消除实验误差，每种算法各进行5次实验，并对实验结果进行平均处理。结果如表1、表2所示。

图2 几何算法示意图

图3 几何算法流程

12345遗传算法1.0251.2521.3251.4551.345A*算法0.0330.0750.1540.2480.187混合算法0.0130.0250.0280.0450.030

表2 三种算法的路径长度比较

通过对比实验结果可知：

运行时间方面，混合路径规划算法的运行时间最少，而遗传算法和A*算法的运行时间多。混合路径规划算法的运行时间最少的原因在于路径规划时，仅判断与起始点和目标点连线相交的障碍物，规划空间中障碍物多边形顶点数量减少，路径方向角计算简单，提高了算法运行效率。A*算法通过计算启发函数估价待扩展节点的值，需要扩展到整个规划空间才能搜索到理想路径。遗传算法在进行路径规划时，需要循环迭代计算，运行时间最长。

路径长度方面，混合路径规划算法通过改进抗体编码和算子设计，可以避免不可行路径的产生，改善路径质量，路径长度最小。A*算法对启发函数的依赖性强，不能保证每次都搜索到最优路径，有可能是次优路径。遗传算法由于本身参数优化问题，容易陷入局部最优。

3.2 仿真实例

以某型装甲分队作战仿真系统山地作战仿真实验为背景，将装甲车辆CGF加入到具有逼真地形地貌、地表特征和自然景象的虚拟三维战场环境中，检验混合路径规划方法在作战仿真系统中的实用性。装甲车辆CGF路径规划过程如图4所示，图4(a)中A、B两点是装甲车辆CGF通过全局路径规划搜寻的两个路径点，当机动至路径点A时，探测到前方新出现一个弹坑，此时再调用局部路径规划模块，运用几何算法规划得到新的路径点H，并机动至该点，如图4(b)所示。待装甲车辆绕过弹坑后，继续回到路径点B上按照初始全局路径行进，如图4(c)所示。

实验表明，应用混合路径规划方法的装甲车辆CGF能够在虚拟战场环境里根据地形信息选择机动路线，实现良好的路径规划，满足作战仿真系统的实时性要求。

图4 装甲车辆CGF路径规划场景

4 结论

1) 提出一种混合路径规划方法，分别运用IGA实现全局路径规划和几何算法实现局部路径规划并应用在一个具体的作战仿真实验中。

2) 该方法能够规划出合理的路径，满足作战仿真系统的实时性要求。