演化折现Hamilton-Jacobi 方程粘性解收敛问题的一个反例

李 霞， 陈苏婷

（苏州科技大学 数学科学学院，江苏 苏州 215009）

令M 是一个连通、光滑的流形，对于M 上的演化Hamilton-Jacobi 方程

考虑其粘性解在t→+∞时的收敛情况，其中g（x）∈C（M）是初始值，R+=[0，+∞）。 对演化Hamilton-Jacobi 方程粘性解长时间渐近行为的研究是粘性解理论的一个重要方向，其粘性解在给定初值的情形下是否收敛，以及收敛后的函数的性质都是重要的研究内容。

若Hamilton 函数含有未知函数u，称之为接触Hamilton-Jacobi 方程，与之相关的接触Hamilton 动力系统是Hamilton 动力系统（Hamilton 函数不含未知函数u）的自然推广。 接触Hamilton 动力系统被广泛运用于耗散力学系统[1-2]、热力学系统[3]、平衡统计力学[4]等各个领域。 近年来，研究Hamilton-Jacobi 方程粘性解的PDE 方法与研究Hamilton 动力系统的变分法相互作用， 产生了许多重要且深刻的研究结果。 而Hamilton-Jacobi 方程粘性解的长时间渐近行为是粘性解理论的一个重要研究分支， 如果流形M 是紧的，Hamilton-Jacobi 方程和接触Hamilton-Jacobi 方程粘性解的收敛性结果可参见文献[5－12]。 当底空间M 非紧时，Fathi近期的一篇文章探讨了Hamilton-Jacobi 方程粘性解的存在条件以及在此条件下解的存在唯一性[13]；而在初始值g（x）∈W1，∞（R）的情形下，Barles 构造了Hamilton-Jacobi 方程粘性解的一个发散反例[14]。 对于非紧空间上接触Hamilton-Jacobi 方程粘性解的表达式以及有限性讨论可参见文献[15]。 关于非紧空间上接触Hamilton-Jacobi 方程粘性解的收敛性，笔者研究的结果初步表明，自治的折现演化Hamilton-Jacobi 方程的粘性解在t→+∞时收敛[16－17]。 因此，文中将构造非自治情形下的反例，说明非紧空间上接触Hamilton-Jacobi 方程的粘性解可能发散。

文中研究的演化折现Hamilton-Jacobi 方程

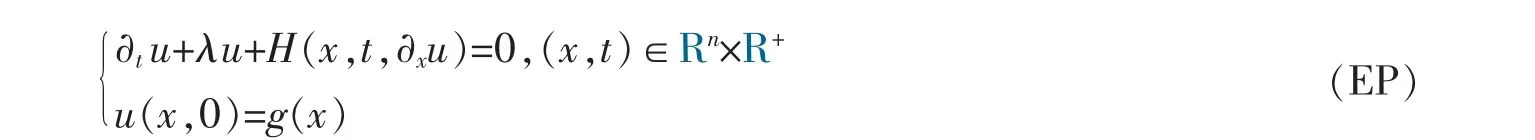
是接触Hamilton-Jacobi 方程的一种特殊形式。 如果不对H 做任何限制， 其解一般不能收敛到稳定情形，例如：u（x，t）＝sin（x+t）是方程ut-ux=0，（x，t）∈R×R+的解，尽管u（x，t）有界，然而t→+∞时，解并不收敛。 由于上述一系列的收敛性结果都需要对H（x，p）有所限制，如H 光滑，关于p 严格凸以及关于p 超线性增长等（Tonelli 条件），笔者也在类似框架下考察非紧空间上折现Hamilton-Jacobi 方程粘性解的敛散性。 由于不需要考虑极小轨道的动力学行为，因此，只需要对H（x，t，p）做出如下限制：

（1）H（x，t，p）在Rn×R+×Rn上连续；

令AC（[0，t]，Rn）＝{γ（t）|γ:[0，t]→Rn，γ（t）是绝对连续}，文中的主要结论如下：在第一节中，将给出（EP）粘性解的表达式。

定理1 令

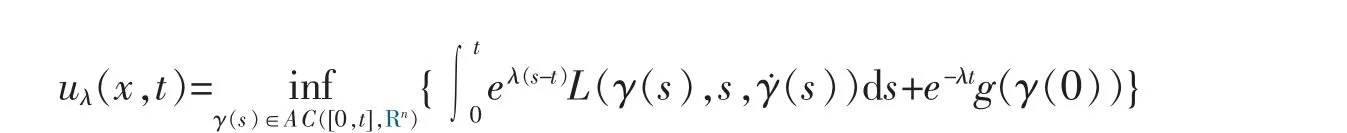
其中γ（t）=x，若uλ（x，t）有限，则uλ（x，t）是演化折现Hamilton-Jacobi 方程（EP）的粘性解。

因为该文的目的在于构建反例，所以只需考虑uλ（x，t）有限时的情形，与文献[15]相比，此处不需要考虑接触Hamilton 系统的动力学性质，所以对H 有较弱的假设。 在第二节通过构造一个具体的例子

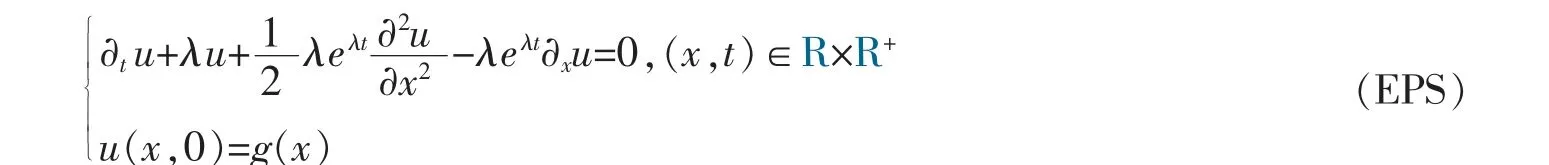
说明存在g（x）∈C（R），使得（EPS）的粘性解在t→+∞时不收敛。

1 粘性解的表达式

下面证明uλ（x，t）是（EP）的粘性下解。 令φ∈C1（Rn×R），（x^，t^）∈Rn×R 使得

2 折现演化Hamilton-Jacobi 方程粘性解的发散反例

定理得证。