巧用“一题多解”渗透数学核心素养

吉林 刘彦永

在传统的接受式教学中，学生的思维往往习惯于求同性、定向性.“一题多解”恰恰是克服学生思维定势的一种有效途径，也是培养学生发散思维和灵活思维的有效方法.通过长期“一题多解”的训练，学生可以从多角度、多途径寻求解决问题的方法，开拓解题思路，并从多种解法的对比中选出最佳解法，总结解题规律，使分析问题、解决问题的能力提高，使思维的发散性和创造性增强，进而提升数学核心素养.数学核心素养离不开具体的情境，只有在解决实际问题中数学的核心素养才能体现出来，没有具体的情境，就无法判断一个人的数学素养的高低.下面以一道高考试题的“一题多解”为载体，浅谈在解题教学过程中如何渗透数学核心素养及其必要性和重要性.

一、试题呈现

试题是以单位圆为载体、向量为背景的最值问题.平面向量是融数形于一体，是代数、平面几何、三角函数、解析几何等知识的交汇点，因而解决此类问题主要是根据向量的数和形的双重特征，并以此为切入点寻求已知与未知之间的内在联系，探究解题的思路和方法.

二、试题解法研究

利用化归思想将向量形式转化为代数中的数量关系，建立关于x+y的函数关系式，从函数的角度来解决问题.

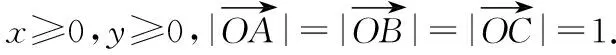
视角1：基本不等式

由(x+y)2≥4xy，

当且仅当x=y=1时取等号，所以x+y的最大值为2.

视角2：对称双换元

令x=a+b,y=a-b，

代入x2+y2-xy=1得a2+3b2=1，

故a≤1，x+y=2a≤2.

当且仅当a=1,b=0，即x=y=1时，x+y的最大值为2.

视角3:三角换元

当α=60°时取等号(经检验符合题意)，故x+y的最大值为2.

视角4:判别式法

令x+y=n(n≥0)，则y=n-x，代入x2+y2-xy=1，

整理得3x2-3nx+(n2-1)=0，

Δ=9n2-12(n2-1)≥0，解得0≤n≤2，

故x+y的最大值为2(经检验符合题意).

【点评】将条件等式两边平方，化向量问题为关于x2+y2-xy=1的代数问题，再从多个角度进行适当处理，解决问题，其中不等式取等号的条件必须加以检验.教师在试题讲解过程中要渗透学生从多角度深刻剖析问题.只有让学生的思维在“多角度”上下功夫，才能取得事半功倍的良好效果，学生的思维在不断的展开中得到充分的训练和培养.

视角1：三角换元

视角2：柯西不等式

也就是(x+y)2≤4，又x≥0,y≥0,即0≤x+y≤2．

【点评】通过建立适当的平面直角坐标系，将向量坐标化，再利用三角换元和柯西不等式求得最值.事实上，建系设C(cosα,sinα)可以直接得到视角1.解法2也可以从线性规划和判别式等视角解决问题，此处不再赘述.因此，教师要培养学生用规律解题，思维线路短，过程简洁，大大提高解题的速度，“触类旁通”的“巧思”也就一定会自然产生.

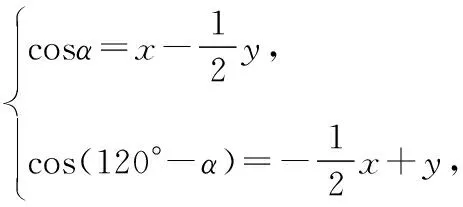
解法4：如图所示，连接AB交OC于点D.

因为A，B，D三点共线，所以λ+μ=1.

所以x=nλ,y=nμ，x+y=nλ+nμ=n(λ+μ)=n.

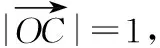
要使x+y最大，必有线段OD最短，

则n=2，故x+y的最大值为2.

【点评】通过建立斜坐标系，将原问题转化为线性规划问题，解法新、方法活，充分地体现了平面向量的代数和几何的双重特征.我们在教学过程中可以渗透给学生敢于打破常规、勇于尝试和探索的精神，让学生在亲身实践中寻求变通，悟出其中的来龙去脉，掌握科学的解题规律和法则.

三、一点感悟

美国著名数学教育家波利亚说过：“掌握数学就意味着要善于解题.”而想要学会解题，好的数学题目是关键.一道好的试题之所以能引起大家的共鸣，不是因为其独特的解题技巧，而是其中所蕴含着的数学思想和方法.本文中的试题就是素材平朴，但求解过程精彩纷呈，妙趣横生，真可谓是一道平中见奇的好题.在日常教学中，教师精心选择这样极具代表性的一题多解题目作为练习，通过一题多解、多题一解的训练，增强学生的数学核心素养.正如波利亚说：“一个专心的认真备课教师能拿出一个有意义的但不复杂的题目，去帮助学生发展问题的各个方面，使得通过这道题，就好像通过一道门户，把学生引入一个完整的领域.”