诊断数列问题中的七种典型错解
2018-07-27四川蔡勇全刘海军
四川 蔡勇全 刘海军
数列是高中数学的重要内容,也是历年高考经久不衰的热点.由于本部分内容所涉及到的概念、公式、性质较多,而且极易混淆,因而在解题时容易出现“会而不对、对而不全、常做常错、一错再错”的现象.本文结合实例诊断数列问题中的七种典型错解,供大家参考.
一、因忽视an=Sn-Sn-1的适用前提而致误
【例1】已知数列{an}的前n项和Sn=2n2-3n+1,求数列{an}的通项公式.
错解由题意,an=Sn-Sn-1=(2n2-3n+1)-[2(n-1)2-3(n-1)+1]=4n-5.
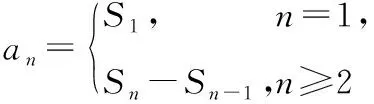
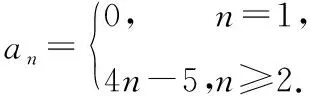
变式1 已知数列{an}的前n项和Sn=3n+2,求该数列的通项公式,并判断数列{an}是否为等比数列.
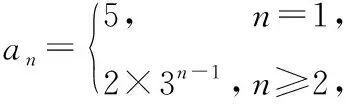
变式2 已知数列{an}的前n项和Sn=aqn(a≠0,q为非零常数且q≠1),则数列{an}为
( )
A.等差数列
B.等比数列
C.既不是等差数列也不是等比数列
D.既是等差数列又是等比数列
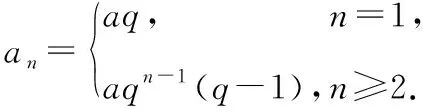
评注上述案例可引申得到如下特殊结论:设数列{an}的前n项和为Sn,若Sn=An2+Bn(A,B为常数),则数列{an}为等差数列(反之亦成立);若Sn=An2+Bn+C(A,B,C为常数且C≠0),则数列{an}从第二项起为等差数列;若Sn=Aqn+B(A,B为非零常数且A+B=0),则数列{an}为等比数列;若Sn=Aqn+B(A,B为非零常数且A+B≠0),则数列{an}从第二项起为等比数列.
二、因忽视隐含条件而致误
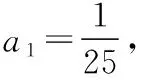
( )
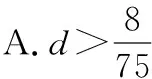
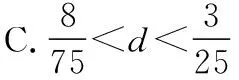
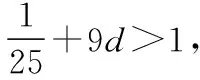
剖析上述解法仅利用到a10>1这一条件,而忽视了关键词中“开始”所隐含的“a9≤1”这一信息,从而造成错解.
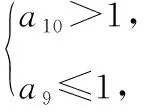
变式1 在等比数列{an}中,a6,a10是方程x2-8x+1=0的两根,则a8等于
( )
A.1 B.-1
C.±1 D.不能确定
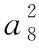
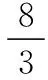

评注在解答变式1时,挖掘出的隐含条件是“a8>0”,在解答变式2时,挖掘出的隐含条件是“y>0”.在数列问题中,由于众多性质、规律的存在,许多特殊的条件常常会隐含在待解的题目中,解答时,要注意根据数列的性质、规律去挖掘出这些隐含的条件.
三、因对数列中有关概念的理解不透彻而致误




变式1 若a,b,c是实数,则“b2=ac”是“a,b,c成等比数列”的
( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
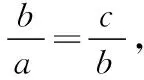
变式2 已知x,2x+2,3x+3成等比数列,且x+1,x+5分别是等差数列{an}的第2项,第4项,求数列{an}的通项公式.
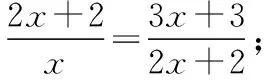
评注解答变式1与变式2,皆需建立在对等比数列的定义“如果一个数列从第二项起,每一项与它的前一项的比值等于同一个常数,那么该数列叫等比数列”有透彻的理解的基础上,尤其是要抓住“比值”这一关键词,否则仅靠“内项之积等于外项之积”得到的结果往往是不完全符合要求的.
四、因对等差数列前n项和公式的理解不到位而致误


剖析上述错解主要体现在忽视了对“在等差数列中,如果公差d≠0,那么前n项和是关于n的二次函数(常数项为0)”这一结论的理解,而在上述解法中,当k是与n无关的常数时,Sn与Tn都是关于n的一次函数,因此得到的结论就必然是不正确的.



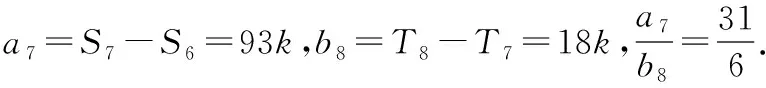
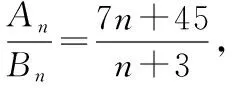
( )
A.3 B.4 C.5 D.6

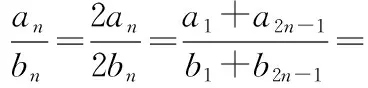
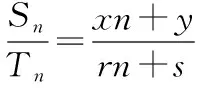
五、因忽视项数n的特殊性而致误
【例5】已知{an}的前n项和Sn=2n2-18n+9,则Sn的最小值为_______.
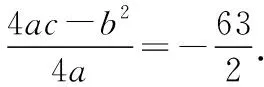
剖析上述解答忽视了n是正整数这一特殊背景,同时,Sn在取得最小值时n的取值也一定是某一个正整数值,而上述解法根本没有考虑到这一点,因此造成错解.
正解因为当x=4.5时,y=2x2-18x+9取得最小值,而n∈N*,由抛物线的对称性可知,n=4或5时,Sn最小,最小值为S4=S5=-31.

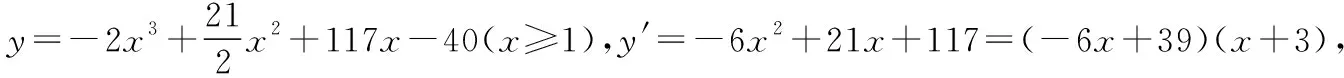
变式2 已知数列{an}的通项公式为an=n2+λn(n∈N*),若数列{an}是递增数列,求实数λ的取值范围.
提示因为数列{an}是递增数列,所以an+1-an>0对于任意n∈N*恒成立,即(n+1)2+λ(n+1)-(n2+λn)>0对于任意n∈N*恒成立,也即λ>-(2n+1)对于任意n∈N*恒成立,因为-(2n+1)的最大值为-3,所以λ>-3,故λ的取值范围是(-3,+∞).
评注从上述案例可以看到,忽略项数n为正整数这一背景,实质就是忽略了数列的离散性,从而用连续代替离散,那么无疑会扩大相应函数的定义域,求出的函数最值或参数的取值范围就会出现偏差.
六、因未实施分类讨论而致误
【例6】已知数列{an}是等比数列,Sn是其前n项之和.
(Ⅰ)求证:S7,S14-S7,S21-S14成等比数列;
(Ⅱ)设k∈N*,试问:Sk,S2k-Sk,S3k-S2k是否能组成等比数列?
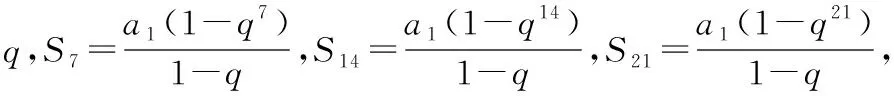
(Ⅱ)类似(Ⅰ)题可证:Sk,S2k-Sk,S3k-S2k一定能组成等比数列.
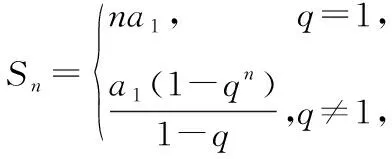
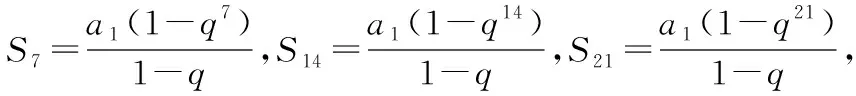
(Ⅱ)①当q≠-1时,对任意k∈N*,Sk,S2k-Sk,S3k-S2k一定能组成等比数列;②当q=-1时,若k为正奇数,则Sk,S2k-Sk,S3k-S2k一定能组成等比数列;若k为正偶数,则Sk=0,S2k-Sk=0,S3k-S2k=0,此时Sk,S2k-Sk,S3k-S2k不能组成等比数列.
变式1 对于数列{rn},若存在常数M>0,对任意的n∈N*,恒有|rn+1-rn|+|rn-rn-1|+…+|r2-r1|
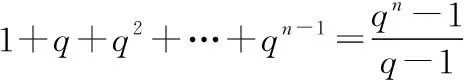
综上所述,当0
变式2 已知正数a,b,且a,x1,x2,…,xn,b成等比数列,求x1x2·…·xn的值.
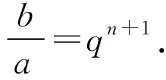

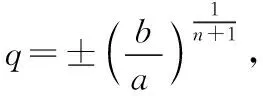
评注数列问题中,当所研究的对象或结果在题目背景下存在多种可能性时,公差、公比、项数或其他参数常常需要进行分类讨论,其中,公比往往是从等于1与不等于1两个角度来讨论的,公差往往是从正、负两个角度来讨论的,项数往往是从奇、偶两个角度来讨论的.
七、因主观臆断、思维定势而致误
【例7】已知数列15,5,16,16,28,试问:该数列的通项公式存在吗?若存在,请指出;若不存在,请说明理由.
错解因为该数列没有任何规律,所以它没有通项公式.
剖析主观上,不少解题者认为,没有规律的数列是没有通项公式的,事实上,对于任意有限数列而言,它都是存在通项公式的,它的各项(共n项)可以看作一个一元n次方程的根.