浅谈“数形结合”思想在高考数学中的应用
2018-07-27甘肃谢彦仁
甘肃 谢彦仁
数形结合,就是根据数与形之间的对应关系,通过把数量关系的问题转化为图形的性质问题去讨论或者把图形的性质转化为数量关系来研究,从而解决数学问题的一种重要的思想方法.
纵观近年来的高考试题,数形结合思想作为一种重要的数学思想方法已成为解答高考数学试题的一种常用方法与技巧,特别是在解决选择、填空题时发挥着奇特功效.巧妙运用数形结合的思想方法解决一些抽象的数学问题,以形助数、以数辅形,可以使抽象的问题直观化、代数的问题几何化、复杂的问题简单化,收到事半功倍的效果.下面根据笔者十几年的教学经验,结合近几年各省市高考题中的实例谈谈自己对巧用数形结合思想解决高考数学问题的一些认识.
一、代数问题“几何化”——以形助数
(一)方程问题中的数形结合
在研究某些方程的根的个数、根的大小以及根的取值范围等问题时,都可以借助于数形结合思想,将抽象的数学语言转化为直观的几何图形来观察方程根的情况.
【例1】(1)已知0 ( ) A.1个_____________________ B.2个 C.3个 D.1个或2个或3个 解析:判断方程的根的个数就是判断图象y=a|x|与y=|logax|的交点个数,画出两个函数图象,易知两图象只有两个交点.故方程有2个实根,故选B. (2)已知α是方程x+log2x=4的根,而β是方程x+2x=4的根,那么α+β=________. 解析:由方程x+log2x=4得log2x=4-x, 由2x+x=4得2x=4-x,作出y=log2x,y=2x,y=4-x的图象,由图象可知直线与两曲线交点坐标为A(α,4-α),B(β,4-β), 而A,B关于直线y=x对称,∴α=4-β,∴α+β=4. (二)不等式问题中的数形结合 在解决一些不会解的抽象不等式时,若利用常规方法无从下手,则可以考虑不等式的两边分别构造函数,在同一平面直角坐标系中作出它们的函数图象,结合图象,数形结合得到它们的解集. 【例2】若不等式|2x-m|≤|3x+6|恒成立,求实数m的取值范围. 解析:在同一坐标系中分别画出函数y=|2x-m|及y=|3x+6|的图象,如图,由于不等式|2x-m|≤|3x+6|恒成立,所以函数y=|2x-m|的图象应总在函数y=|3x+6|图象的下方,因此,函数y=|2x-m|的图象也必经过点(-2,0),所以m=-4,即m的取值范围为{m|m=-4}. 此题属于不等式恒成立问题,先利用图象的上、下位置关系确定直线的位置,然后再还原即可.解不等式或证明不等式问题经常联系函数的图象,根据不等式中量的特点,选择适当的两个(或多个)函数,利用两个函数图象的上、下位置关系来确定不等式的解集或证明不等式. (三)函数问题中的数形结合 【例3】已知函数f(x)=|lg(x-1)|,若a>b,且f(a)=f(b),则a+2b的取值范围是 ( ) C.[4,+∞) D.(4,+∞) 解析:作出函数f(x)=|lg(x-1)|的图象, ∵a>b,且f(a)=f(b),∴1 又由f(x)=|lg(x-1)|得|lg(a-1)|=|lg(b-1)|, 而a-1≠b-1,∴lg(a-1)=-lg(b-1), ∴ab-a-b=0,∴a+b=ab, (四)集合问题中的数形结合 在解决高考中的集合问题时,常常借助于数轴、韦恩图化抽象为具体,化复杂为简单,把集合的交、并、补的关系直观、形象的显示出来,使问题得以简化,运算简洁明了. 【例5】某校先后举行数理化三科竞赛,学生中至少参加一科的:数学807人,物理739人,化学437人;至少参加两科的:数理593人,数化371人,理化267人;三科都参加的213人,试计算参加竞赛总人数. 解析:我们用圆A,B,C分别表示参加数理化竞赛的人数,那么三个圆的公共部分正好表示同时参加数理化小组的人数.用n表示集合的元素,则有n(A)+n(B)+n(C)-n(A∩B)-n(A∩C)-n(B∩C)+n(A∩B∩C)=807+739+437-593-371-267+213=965,即参加竞赛总人数为965人. (五)解析几何中的数形结合 解析几何的基本思想就是数形结合,在解题中要善于将数与形的对立统一巧妙运用于对点、线、曲线的性质及其相互关系的研究中. ∴该抛物线焦点F(0,1),准线l的方程为y=-1, 取P为抛物线上的任一点,过点P作PP′⊥l,垂足为P′, 则P点在x轴上的射影为M(如图所示). 欲使|PA|+|PM|最小,则|PA|+|PP′|最小, 即|PA|+|PF|最小, 解本题时,不少同学可能会依常理“出牌”——构造函数,将问题转化为求函数的最值,然而其最值很难求得.事实上,求抛物线的焦点(或准线)相关的最值问题,更多的是考虑数形结合,利用抛物线的定义进行转化,然后利用三点共线或三角形的三边关系加以处理. 【例7】函数f(x)的图象如图所示,f(x)为奇函数,其定义域为(-∞,0)∪(0,+∞),则不等式x[f(x)-f(-x)]<0的解集是 ( ) A.(-3,0)∪(0,3) B.(-∞,-3)∪(0,3) C.(-∞,-3)∪(3,+∞) D.(-3,0)∪(3,+∞) 解析:x[f(x)-f(-x)]<0,即2x×f(x)<0.当x<0时,则f(x)>0,由图象知-3 从上面的例子可知,在题设情境为图象时,常常需要进行由“形”向“数”的转化,即将形所含的信息转化为数和式的表达式或关系式,以数析形,然后推理求解. ( ) A.2 B.4 C.6 D.8 解析:依题意,两函数的图象如图所示, 由两函数的对称性可知交点A1,A2,A3,A4,A5,A6,A7,A8的横坐标满足x1+x8=2,x2+x7=2,x3+x6=2,x4+x5=2,即x1+x2+x3+x4+x5+x6+x7+x8=8, 故选D. 【例9】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)=f1(x)+f2(x). (Ⅰ)求函数f(x)的表达式; (Ⅱ)证明:当a>3时,关于x的方程f(x)=f(a)有三个实数解. 解析:(Ⅰ)由已知,设f1(x)=ax2,由f1(1)=1,得a=1, 它的图象与直线y=x的交点分别为 (Ⅱ)证明:(方法一)由f(x)=f(a), ∴当a>3时,在第一象限f3(x)的图象上存在一点(2,f3(2))在f2(x)图象的上方. ∴f2(x)与f3(x)的图象在第一象限有两个交点, 即f(x)=f(a)有两个正数解. 因此,在a>3时,方程f(x)=f(a)有三个实数解. 由a>3,Δ=a4+32a>0,得 ∴x1≠x3.故原方程有三个实数解. 在解答此类问题时,教师就要注意引导学生将方程f(x)=g(x)转化成函数,然后在同一坐标系下画出函数y=f(x)和y=g(x)的图象,通过研究函数图象交点的个数,来确定方程解的个数或函数零点的个数. 从以上的内容及分析可知,数形结合思想是高中数学教学中的重要思想之一,而且是一种常用的教学方法.数形结合的重点在于“以形助数”,通过“以形助数”,将抽象的数学语言与直观的几何图形巧妙结合起来,使得复杂的问题简单化,抽象的问题具体化,从数的“定量”和形的“定性”上统一的来解决问题.
















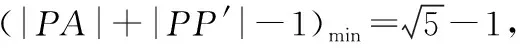
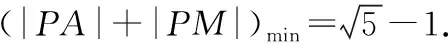
二、几何问题“代数化”——以数辅形



三、数形互化、相得益彰