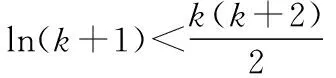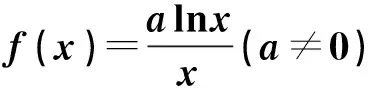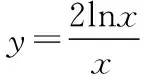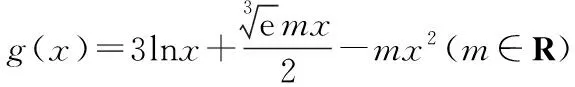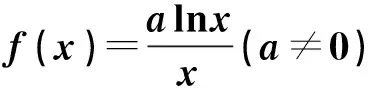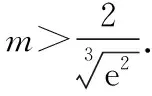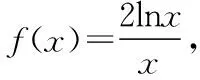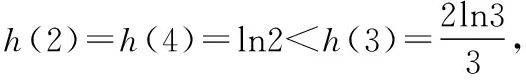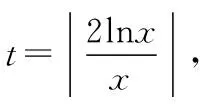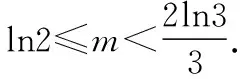以教材的一个常见函数为背景命制原创试题

安徽 张 威 蒋玉芳

我们知道原创试题是教师的一项重要的、经常性的工作．原创一份高质量的数学试题，不仅能让教师准确地了解教学效果，还有利于提高学生的数学能力．每位教师原创试题的手段又是多种多样的,对于笔者来说，原创的试题主要有两个来源：一是通过教材的重要知识点新编试题；二是通过经典的高考或模拟题进行改编．本文主要介绍“通过教材的重要知识点新编试题”.以下是笔者通过教材上的一个重要函数进行原创试题的一些感悟.

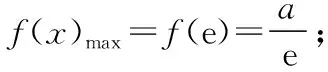
又当x>1时，f(x)>0；当0

又当x>1时，f(x)<0；

当00.

故大致的图象如下：

我们的目标是要证明:

由归纳假设,我们得到了①,下面我们用分析法来证明②式.

只需证ln(k+1)2

因为lnx≤x-1,

令x=(k+1)2,即ln(k+1)2≤(k+1)2-1,

也就是ln(k+1)2

学生反思过程中，对上题的思路过程进行进一步的整理和提炼，可以应用上面题的一些思路，一些方法.对比两题的结果，大家可以知道其实是同一个题型以不同的形式呈现给了学生，倘若学生停留在解决这个题，那只能是愚公移山，费时费力，这样学生会后劲不足，学习动力欠缺，只有不断反思思路过程,解题方法，才能举一反三，思维敏捷，事半功倍.

数学经典函数lnx≤x-1及其应用同样出现在2017年普通高等学校招生全国统一考试(全国卷Ⅲ)理科数学中.

(作者单位：广东省中山市第二中学)

【点评】实数a的大小及正负决定该函数的单调性和最值，在原创和该函数有关的试题时，可以根据需要对a进行赋值，使得数据或者其它方面更完美.

接下来笔者以该函数为背景,以函数零点问题和含参不等式问题为命题点进行命题.

1.考查分离参数法和数形结合思想

【原创1】若函数g(x)=2lnx-mx(m∈R)存在两个不同的零点，则m的取值范围是________.

2.考查分离函数法和数形结合思想

【原创3】已知函数f(x)图象与函数g(x)=-2ln(-x)+mx2+2的图象关于点(0,1)对称，若函数y=f(x)有两个不同的零点，则实数m的取值范围是________.

【命题思路】此题是以【原创2】为背景，把函数对称性与函数零点交汇考查，那么可能读者会问，函数g(x)=-2ln(-x)+mx2+2是怎么想到的呢？其实很简单，是在题目“若函数f(x)=2lnx-mx2有两个不同的零点，则实数m的取值范围是________.”基础上填充交汇的知识点，即求函数f(x)=2lnx-mx2关于(0,1)的对称函数即可.通过此题的命制思路，可进一步命制考查轴对称、奇偶性等试题.

【命题思路】了解此题的本质为“设函数y=-mx2(x<0)关于原点对称的函数为g(x)，若方程g(x)=2lnx有两个不同实根，则实数m的取值范围是________.”再根据【原创2】、【原创3】即可进一步了解此题的来龙去脉.

3.考查二次函数型函数零点和数形结合思想

【原创5】已知函数g(x)=8e(lnx)2-(2e+8)x|lnx|，f(x)=-2x2，则方程g(x)-f(x)=0的实数根个数是________.

【本题答案】4.

【原创6】已知函数g(x)=4e(lnx)2-(2em+4)x|lnx|+2mx2，若函数g(x)有5个不同的零点，则实数m的取值范围是________.

1.考查分离函数法和导数的几何意义及数形结合思想

【原创8】已知函数f(x)的图象与函数g(x)=-4ln(-x)-kx+2的图象关于点(0,1)对称，若存在有且只有两个整数x满足不等式f(x)>kx2，则实数k的取值范围是

( )

【本题答案】D.

2.考查一元二次不等式、数形结合思想和分类讨论思想

【命题思路】利用一元二次不等式解法和函数图象及性质命制.

【本题答案】m>-2e.

【原创10】已知函数g(x)=4e(lnx)2-(2em+4)x|lnx|+2mx2，若关于x的不等式g(x)<0恰只含有一个整数解，则实数m的取值范围是________.

综上所述，命制新题时需要注意以下几个方面：

(1)选择命题点，只有命题点确定，才有命题的方向；

(2)构造实质性的基础题目并研究其可行性，通过对基础题目的研究，才能更清晰、更准确、更完美的命制出需要难度的新题；

(3)填充需要的交汇的知识点，对于交汇知识点的填充，要根据题目难度、高考以及基础题目的本身进行填充；

(4)对题目进行重组和变化基础题目的形式，因为基础题目一般很容易就能看出题目的本质，所以需要对基础题目和交汇知识点进行重组和变化，使得题目的本质被掩盖，这样更能考查学生的分析和解决题目的能力;

(5)进一步对题目进行打磨，主要从科学性、逻辑性、独立性以及语言表达等方面做最后的审定和修改．