基于四参数-ICP的点云配准研究

刘 盈 吕开云

（东华理工大学测绘工程学院 江西南昌 330013）

1 引言

目前，三维激光扫描技术已经在各个领域得到了广泛的应用，在利用该设备对目标物进行扫描的过程中，需要设置不同的站点来获取目标物整体点云，而不同站点就需要点云的配准，而对点云的配准有两种方法，一种是基于标靶的配准，一种主要是利用ICP的无标靶配准，而无标靶配准方法主要有四元素法、罗德里格矩阵法及六参数法等，这三种方法只有在获取高精度的标靶中心情况下，才能得到精度较高的配准。基于ICP算法的无标靶配准，该方法的核心是搜索同名区域点云的对应点，并将搜索到的对应点引入到四元素算法中，从而完成配准，该方法的缺点是在对应点搜索的过程中容易陷入局部最小，且消耗时间很长，并且容易受噪声的影响。在利用ICP算法进行配准的过程中，其中一个非常关键的问题是对应点的搜索，而对应点的搜索往往是需要消耗时间的关键因素，针对此，采用了多维二元搜索树算法，该算法一方面可以降低搜索时间，另一方面也具有抗粗差性。对于特殊目标物，如建筑物，存在大量平面特性，可以利用几何特征约束的建筑物点云配准算法，该算法有效的利用了共面信息，并将共面的约束条件作为六参数配准的约束条件，从而提高了配准的精度。在同时考虑平面特点和对应点搜索速度的情况下，可以利用平面特征和最邻近点搜索算法（KNNS）提高点云配准效率。

以上方法虽然对现有的ICP配准算法进行了改进和优化，但是无法保证对应点搜索的过程中不会出现重复，同时没有初始配准作为支撑，则很难保证ICP对应点搜索不会陷入局部最小。针对此，本文将四参数算法和改进的ICP算法进行组合，该算法一方面考虑了初始配准的作用，另一方面考虑了ICP算法配准过程中容易出现同名点重复的问题，同时考虑了整体配准精度的均匀性。因此，该算法即能解决基于标靶配准的配准精度不均匀问题，又能解决ICP配准算法效率问题。

2 四参数坐标转换模型

假设扫描的过程中，有两个控制点A、B两点，由于在扫描的过程中三维激光扫描进行整平，所以可以不考虑z轴的旋转，则测站1扫描两个控制点得到 A 点坐标为（xA，yA），B 点坐标（xB，yB），测站 2扫描两个控制点得到 A 点坐标为（x′A，y′A），B 点坐标（x′B，y′B），按照平面坐标系进行转化。

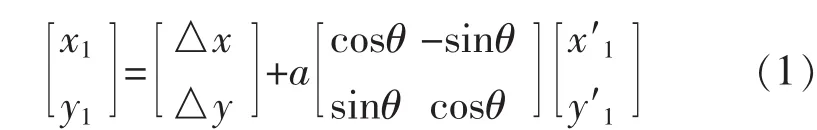
式中：a为尺度变换参数，x′1y′1为转换后坐标，为转换前坐标。当采用三维激光扫描时，由于扫描区域较小，取a=1。

令 cosθ=c，sinθ=d，带入式（2）得到：

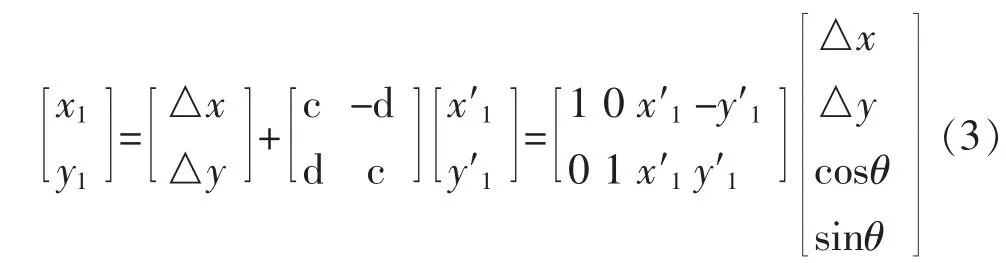
方程L=BX，利用平差公式V=BX-L，求解：

可以解出三个参数△x、△y、旋转角度θ。

两期点云在Z轴上的差值△Z可用下式计算：

从而可以求出四个参数△x、△y、△Z、旋转角度θ。

3 改进的ICP算法

ICP算法的核心是先利用初始的同名点进行初始配准，然后再利用同名区域进行两期邻近点的寻找，从而根据目标函数进行算法迭代，直到函数值不发生变化。假设两个坐标下的点集为和，求取配准参数的过程就是确定两个点集同名点之间距离平方和最小，如式（6）所示

式中：R为旋转矩阵，T为平移矩阵

战略柔性是企业技术创新的源泉，是企业高效利用资源的重要保障。通过增强战略柔性，提高资源柔性和协调柔性水平，增强中小企业自主创新能力，提高生产效率，先于竞争对手进入新市场。

设定Ui为目标点集，Mi为参考点集，则改进的ICP算法如下

（1）初始化旋转矩阵R0和平移参数T0。

（2）利用公式（6）对点集Ui进行配准，得到点集Uˆi。

（3）按顺序计算Uˆi中的每个点集到 Mi中的所有点集之间的距离，根据距离最小原则对Mi进行重采样，得到一组新的点集Mi，新Mi满足的条件如下式所示：

根据式（8）可知，在进行点集采样的过程中，不仅会落入局部最小的陷阱，而且也会影响搜索速度，即

为了避免点集搜索重复的问题，可以对每次搜索到最邻近点进行删除，如下式所示：

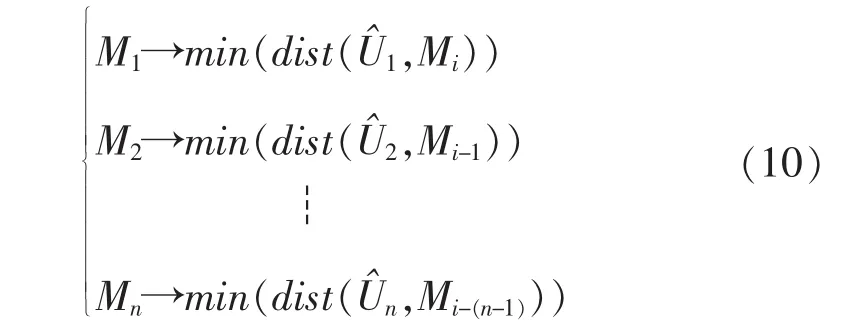
（4）利用四元素算法对新的对应点集Mi和Uˆi求解得到新的旋转矩阵R和平移参数T，并将新得到的旋转矩阵R和平移参数T代入到步骤 （1），继续计算，形成迭代过程，直到满足两点集目标函数式（6）的同源点间距离的平方和最小的要求，迭代停止。

改进的ICP算法如图1所示

4 固定同名区域的确定

图1 改进的ICP流程

在利用四参数-ICP进行点云配准的过程中，ICP配准的关键是固定同名区域的确定，传统的该区域的确定方法是手动的确定，虽然可行，但是影响效率，同时也无法保证两期点云的完全同名区域，另外手动方法确定的点云还有可能夹带噪声，从而影响ICP的精配准精度，针对此，本文提出了固定同名区域确定方法，该方法的主要步骤是首先对两期点云数据进行粗配准，然后计算两期点云的邻近点距离，假设第一期点云数据表示为（xi，yi，zi），经过粗配准后的第二期点云数据表示为（x′i，y′i，z′i），两期点云邻近点距离，如式（11）所示

由式 （11）计算得到的两期点云数据邻近点距离，即为经过配准后两期点云数据邻近点的偏差，造成该偏差的主要原因是配准。而如果两期点云没有发生变形，则两期点云邻近点距离也存在着限差，根据限差公式，即邻近点距离不会超过3倍中误差，超过的部分视为变形引起的或粗差引起的，小于限差的视为固定同名区域，基于此原理，根据式（11）计算得到两期点云邻近点偏差的中误差为

根据式（11）便可得到邻近点偏差阈值为

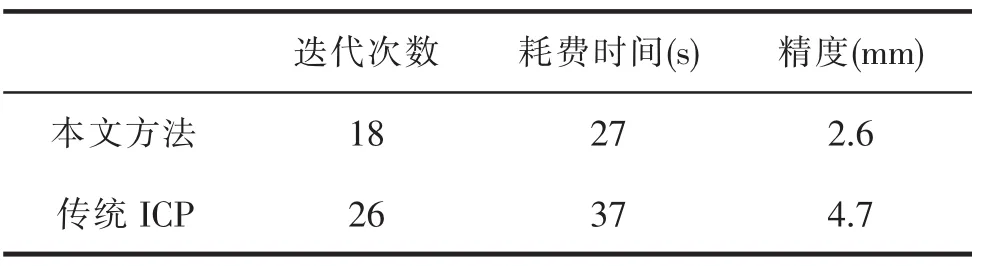
将di与Threshold进行比较，提取di

5 实例分析

5.1 采集点云数据

本文使用Leica-P40扫描仪对球型标靶及可能发生变形的区域进行扫描，进行四参数-ICP点云配准验证实验。扫描现场布置四个球型标靶，如图2中矩形框所示，分别在两期进行扫描，得到两期的点云数据。

图2 布设的标靶球

为了验证本文提出的算法的效果，需要采集四个标靶点云，如图3所示。

图3 采集的球心标靶点云数据（第一行是第一期，第二行是第二期）

为了对该配准算法进行验证，利用三维激光扫描进行目标物扫描的时候，获取了不同期区域点云数据，如图4所示

图4 现场扫描点云数据

5.2 配准结果对比

利用本文方法对两期点云进行对比分析并将配准结果和传统四元素及ICP方法进行比对，以确定本文提出的配准方法的有效性。

利用本文方法对两期不同坐标系统下的点云进行配准，并将配准结果与传统ICP算法进行比较，结果如图5所示。

图5 本文和ICP配准方法对比

由图5矩形方框中的细节可以明显的发现，本文提出的配准方法能够将两期点云很好的融合，而ICP方法出现了两期点云契合偏差现象，造成该现象的原因是在邻近点搜索的过程中陷入了局部极小。同时本文方法在进行ICP迭代计算的过程中，其迭代的次数及耗费的时间明显优于传统的ICP方法，且配准精度要高于传统ICP方法，如表1所示

表1 不同方法不同配准结果参数对比

6 结束语

本文主要研究了三维激光扫描的配准，首先分析了传统点云配准的优缺点，针对传统的六参数、四元素等基于标靶的配准方法存在区域配准精度低及ICP配准时间长等问题，研究了四参数配准的基本条件，分析了ICP算法中存在的缺点，通过逐步搜索逐步剔除的方法实现搜索重复的避免，并进一步加速了ICP的配准，在仪器粗整平的基础上，利用四参数进行点云坐标的粗转换，利用同名区域，结合改进的ICP算法，在只有两个标靶的情况下，实现点云的精配准。