球形标靶的固定式扫描大点云自动定向方法

姚吉利，马 宁，贾象阳，徐广鹏，谢建春

1.山东理工大学建筑工程学院，山东 淄博255000；2.山东省地质测绘院，山东 济南250014

1 引 言

自2000年初以来，地面扫描技术（terrestrial laser scanning，TLS）由研究阶段发展成为顶级的商业化地理数据技术［1］。随着三维激光扫描仪硬件性能的提高，3D扫描技术日趋成熟［2］。在地形测量应用方面，文献［3］于1992年尝试将其用于地形测绘并建立DEM；文献［4］用GNSS、TLS和TSS（Total Station Survey）联合技术进行1.6km2地形测量。TLS地形测量的首要任务是将每站扫描点云坐标转换到地形测量指定的坐标系中（国家或地方坐标系统，以下称为指定坐标系）［1－5］。坐标转换要用到6个坐标转换参数（6DOF）［6－7］，其几何意义如图1所示。

图1 点云定向参数Fig.1 Orientation byφ、ω、κ

坐标系o－xyz原点为扫描仪光电中心，z轴是仪器的竖轴，即仪器旋转轴，y轴为仪器扫描平面的起始方向，x轴与前两轴垂直并构成一个右手系。扫描仪中心o在指定坐标系O－XYZ中的坐标（XS，YS，ZS），表示扫描站的位置；φ（rolling）是x轴与x轴在XZ平面上投影之间的夹角，ω（pitch）是y轴与y轴在YZ平面上的投影之间的夹角，κ（yaw）是x轴与x轴在XY平面内投影的夹角。φ、ω、κ确定了点云在O－XYZ的姿态，称为姿态参数。点云在指定坐标系的位置称为定向参数。从几何意义上讲，确定点云位置参数XS、YS、ZS和姿态参数φ、ω、κ的过程，称为点云的定向与定位［2，8－9］，简称点云定向。对于扫描坐标 系到指定坐标系的变换，目前有间接定向法和独立模型定向法两种途径。间接定向法就是先对各站刚性点云进行拼接形成整体点云（此过程称为点云相对定向），然后选出至少3个标准控制点，对相对定向后的点云进行绝对定向［4，9－10］，拼接方法是已经发展成熟的ICP及改进的ICP算法［11－16］，绝对定向是常用的7参数三维坐标转换模型；独立模型点云定向法以标靶中心为标准控制点（每站3个以上标靶），用全站仪/GNSS/水准仪测量标准点在指定坐标系中的三维坐标，在点云中识别并获取标靶中心的扫描坐标，平差求解点云定向参数，实现点云定向［1，8－9］。

为了获取标准控制点坐标，往往布设人工标志或定向标靶［1，4］，如平面反射标靶、球形标靶等。球形定向标靶相对于反射片的优点是：①识别距离远，反射片是根据强反射率高密度点或影像识别标靶，识别距离不超过200m；球有固定形状，用4个以上球面扫描点便可计算球心坐标，可放置得更远；②无论从什么方向扫描球形标靶，球心坐标都可拟合出来，而反射片要求与扫描激光束基本垂直；③制作方便，专用标靶造价昂贵，球形标靶可用普通材料（白色塑料）制作；④球形标靶可用于高精度的仪器指标检测。文献［16］用直径为76.2mm和145mm的白球测定扫描仪的测角误差和距离误差，认为单个点云无法测量其误差，只能通过对球面进行拟合得到球心坐标，再通过球心之间的已知距离比较来评定，由此测定了Leica ScanStation、Trimble GX、Z＋F Imager 5006和FARO LS880 4种仪器的精度；文献［17］也用白球测定10多种扫描仪在扫描方向上的距离误差；文献［18］也用大小不同的球对高分辨率扫描数据进行误差分析。因此，选择圆球作为定向标靶效果最好。

根据目前地面三维激光扫描数据获取速度快、数据量大、测量距离远、点云定向数据处理相对滞后、自动化程度低、不能适应远距离地形测量的现状，提出一种基于远距离标靶识别的点云自动定向方法：主要根据远距离标靶表面点稀少，误差较大的特点，以远距离标靶自动识别为主要研究目标，结合标准控制点在指定坐标中的信息，使标靶扫描坐标与指定坐标系坐标一一对应，自动解算点云定向参数，进行坐标转换。

2 大点云的标靶探测原理

2.1 确定标靶所在点云环、点云带

根据扫描站和标靶控制点在工程测量坐标系的最远距离和最近距离，计算点云环的内径R1和外径R2，从原始点云（图2（a））中提取标靶所在的点云环，如图2（b）所示。根据野外用GNSS/全站仪测量的扫描站坐标和N个标靶中心坐标，计算各标靶到扫描站在工程测量坐标系的距离Si（i＝1，2，…，N），按式（1）计算每个标靶所在点云带的内径和外径

式中，Δ为标靶所在点云带的宽度，依照最大球形标靶的半径的2～3倍。

2.2 点云扇形等距空间索引

现有的点云空间索引建立的方法有k－d树索引结构［19］、十叉树空间索引［20］和球形空间索引等［7］。环形点云带按等距离分区，建立点云扇形等距平面索引数据库，如图2（d）所示，无论标靶离扫描站多远，设扇形小区的内弧的长度与点云环的宽度相等（为Δ），这样就使离扫描站不同距离的扇形区的大小基本一致，只有外弧长稍大一点。在同一个点云环上，各扇形小区对应一个相同的圆心角θ，用各点方位角除以θ，得到各点的区号，然后对点进行编码，编码长度为5位，第1位是标靶号，后4位是扇形区号，同一个区内的点具有相同的编码。该方法与矩形分区［21］的不同在于，矩形分区时，球面上的点最多可能分布在4个区域，而扇形结构搜索时，则球上的点最多分布在两个区域。

图2 标靶所在点云Fig.2 Point cloud with targets

2.3 候选标靶点确定

要探测的球形标靶如图3（c）所示，以一个点云带为一个搜索区，以每个扇形为探测单元进行探测；图3（a）和图3（b）为有标靶的单元点云。把每个单元的Z坐标按d＝1.95r0（r0为标靶球的已知半径）等分成若干个格，d的大小基本就是标靶表面点云直径，用每格内的点进行球面拟合［22］。标靶表面点满足

式中，x、y、z是球面扫描观测点三维坐标；a、b、c、r表示球心三维坐标和球的半径（称为未知几何参数），展开成二次多项式

式中，A、B、C、D是拟合参数，由用4个扫描点可唯一解得。实用时球面点多于4个，由于扫描点坐标误差的影响，式（3）变为

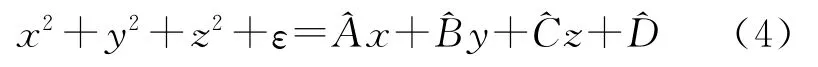
在最小二乘原则εTε＝min下，求解拟合参数平差值，不用计算拟合参数的初值。按式（5）由拟合参数平差值，计算未知几何参数平差值

当与已知半径r0之差在2σ（σ为扫描仪的三维点位中误差，由仪器厂家给出）之内，则该点云带内可能有标靶，此时标靶为候选标靶，并记录拟合半径和球心坐标（如本案例中有18个候选标靶），而后将圆球度在85%以上的候选标靶记为可信标靶（6个），圆球度C定义如下

式中，dist（O，pk）为球面点到球心的无符号距离函数。

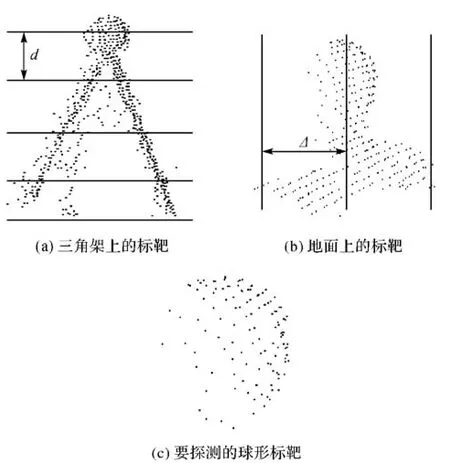
图3 标靶Fig.3 Spherical target

2.4 确定真标靶

一个点云带中，可信标靶可能多于1个，原因有二：其一是球可能分布在相邻扇形区，或相邻格子内（图2（a）和2（b）中出现重复球的现象）；其二是点云环内有与标靶大小基本相等的假标靶球，因而需要删除重复的标靶和假标靶，并重新拟合真球心坐标。

2.4.1 删除重复标靶

假设球面上的点分布在相邻扇形区或上下格内，要拟合的球心坐标基本相等，如果两个球之间的距离之差在一定范围（如3σ）之内，则应保留圆球度高的一个。

2.4.2 删除假标靶

删除假标靶的方法是用全组合距离匹配法，设真标靶有n个，以图3（n＝4）为例，删除一个假标靶的步骤是：

（1）计算任意两个标靶在指定坐标系的全组合距离，记为

式中，i＝1，2，…，n；j＝1，2，…，n；i≠j。

（2）计算每个可信标靶扫描距离匹配系数ρT。一个扫描距离DS的匹配值T定义为

标靶k扫描距离匹配系数ρTk按式（9）计算

（3）当ρTk＜0.5时，标靶k为假标靶。图4中标靶5的扫描距离匹配系数ρT5＝0，其他扫描距离匹配系数均为1。

图4 标靶距离Fig.4 Distance between targets

2.4.3 标靶球心坐标计算

同一标靶表面点可能分布在相邻两个格内，所以从点云带中提取完整表面点进行第2次拟合，计算各点拟合误差dn

拟合误差σn为

式中，N是拟合点个数。为了提高标靶中心拟合精度，应删除误差大的噪声点，如图5（a）的红色点，噪声点可以认为是dn＞2σn的点，用去噪后的点云（图5（b））进行第3次拟合，求解标靶球心坐标。

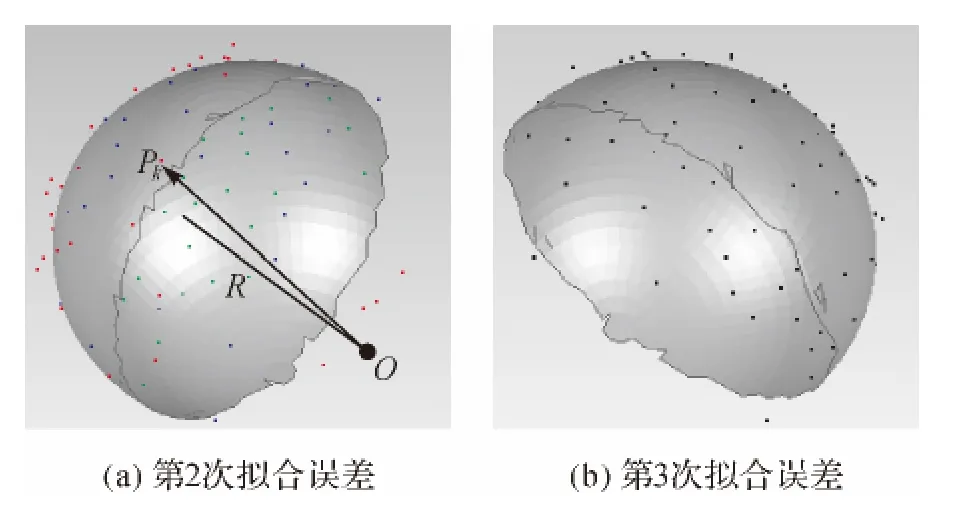
图5 拟合误差Fig.5 Fitting sphere

3 点云定向

用标靶中心的指定坐标和拟合坐标平差计算的点云定向参数，组成定向矩阵P定义为

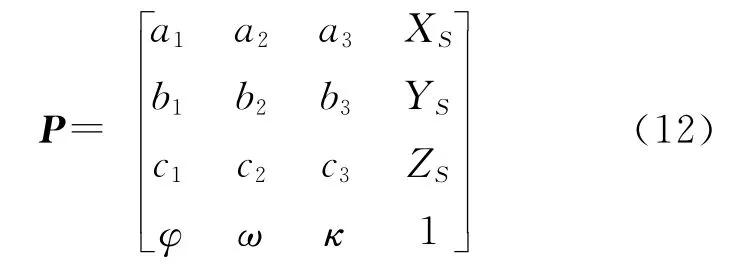
式中，XS、YS、ZS为扫描仪中心在指定坐标系的坐标；a、b、c是反对称矩阵［23－25］中3个元素；λ是缩放因子，一般取1。其他9个元素是点云绕3个坐标轴3个旋转角的函数，构成旋转矩阵，表达了扫描时仪器在扫描时的姿态。

而后将扫描仪坐标系坐标转换到工程指定坐标系下。

4 试验及分析

4.1 试验数据介绍

本试验所用数据来自某矿山，矿区大小为3.2km×2.8km，扫描仪器为 Riegl VZ－1000。共扫描47站点云，每站布设4个定向标靶，2个为检核标靶，标靶到扫描站的距离在70～273m之间。球形标靶放在有水准管的三角基座上，如图6所示，用GNSS RTK测量地面点坐标，量取标靶高后将指定坐标系坐标引入到球心。每站约得到1亿个扫描点，数据处理使用IDL语言开发的基于激光点云的EEXLT（地图要素提取）软件。工程指定坐标系采用1980西安坐标系，以高斯东坐标为X，高斯北坐标为Y，85高程为Z，构成右手三维坐标系。

图6 球形标靶Fig.6 Spherical targets

4.2 标靶自动探测结果分析

以第2站扫描数据为例，来说明本方法的可行性。建立等距离扇形索引后，对每个扇形区点云进行探测和球面拟合，拟合半径与标靶球理论半径相差不大于1cm时，则认为该区可能有标靶（候选标靶）。计算结果显示共有18个候选标靶，见表1。

表1 候选标靶Tab.1 Candidate targets

然后计算候选标靶的圆球度，圆球度大于85%的可信标靶有6个，见表2。根据删除重复标靶的原理，删除重复标靶后，得到5个标靶，其坐标数据列于表3。

表2 可信标靶中心坐标Tab.2 Trusted ball center coordinates

表3 标靶中心扫描坐标成果Tab.3 Target center scan coordinate results

4.3 精度及实用性分析

4.3.1 三项误差分析

将标靶中心扫描坐标转换到指定坐标系的坐标称为转换坐标，用GNSS RTK/全站仪测量的球心坐标称为观测坐标，转换坐标与观测坐标之差称为坐标转换误差。根据坐标转换误差计算的每个标靶的平面误差和三维空间误差及高程误差（统称三项误差）。前6站20个定向标靶的三项误差见图7。

图7中横坐标为标靶序号，纵坐标为误差（单位为m）。由图7中三项误差分析可以看出，高程误差整体上低于平面点位误差和空间点位误差。根据三项误差可以计算出，6站整体的平面点位中误差为12.6mm，空间点位中误差为16.0 mm，高程中误差为10.0mm。

图7 定向标靶三项误差分析Fig.7 Three errors analysis of targets

4.3.2 实用性分析

为了证实本方法的实用性，笔者用不同大小的点云，在不同配置的计算机上进行自动定向，对运行时间（读取时间、探测标靶时间、坐标转换时间、写二进制数据文件时间的总和）进行了统计，结果见表4。

表4 运行时间Fig.4 Running time

RiSCAN PRO和Geomagic Studio 9打开3000万个点（内存2GB的计算机），要用5min以上的时间，所以本文方法明显是更有效率的。

5 结论与展望

通过本文的研究得出如下结论：

（1）扫描时，布设3个以上的球形标靶，标靶表面上落的点多于4个时，就能实现标靶的自动探测、单站定向参数计算和坐标转换。文献［20］认为在交互式点云拼接等处理中需要大量人工干预（60%以上），而本文定向方法不需要人工干预。

（2）独立模型法定向对计算机的硬件配置没有特殊要求，方便普通电脑使用。

（3）球形标靶有固定形状和大小，并能进行较远距离的自动几何识别，平面反射片标靶是根据反射率来识别的，其点云形状随其表面上的点数量变化会发生变形，因此不能远距离使用。

（4）根据GNSS/全站仪测量的标靶和扫描站数据，通过点云分段读取107 151 326（占磁盘空间2.85GB）个点，标靶在可能的点云环上的128万个点中找出，这样就使标靶搜索率从100%提高到了1.2%；建立各点云环扇形索引，自动探测标靶、平差计算坐标转换参数，实现了绝对定向的自动化。

（5）实用中，球形标靶放置在点云中等密度区，一般离扫描站0.1～0.3D（D为有效测程），标靶均匀分布在扫描站四周、高低错落，相邻站重叠区域至少有2个标靶连接。

（6）点云定向精度会直接影响到点云处理［26］，标靶球的自动探测将为后续的光束法区域网平差的点云定向作好准备［27－28］。今后将在扫描站和标靶构成图形结构、分布标靶表面去噪、坐标参数高精度求解等方面作更深入的研究，全面提高自动定向精度。

［1］LEMMENS M.Terrestrial Laser Scanning［M］∥LEMMENS M.Geo－information.Netherlands：Springer，2011：101－121.

［2］WANDA M，BERNER A，BOKELOH M，et al.Processing and Interactive Editing of Huge Point Clouds from 3D Scanners［J］.Computers ＆ Graphics，2008，32（2）：204－220.

［3］ROHRSCHNEIDER K，BURK R O，VÖLCKER H E.Reproducibility of Topometric Data Acquisition in Normal and Glaucomatous Optic Nerve Heads with the Laser Tomographic Scanner［J］.Graefe’s Archive for Clinical and Experimental Ophthalmology，1993，231（8）：457－464.

［4］CASULA G，MORA P，BIANCHI M.Detection of Terrain Morphologic Features Using GPS，TLS，and Land Surveys：“Tana Della Volpe”Blind Valley Case Study［J］.Journal of Surveying Engineering，2010，136（3）：132－138.

［5］BARNEA S，FILIN S.Key Point Based Autonomous Registration of Terrestrial Laser Point－clouds［J］.ISPRS Journal of Photogrammetry ＆Remote Sensing，2008，63（1）：19－35.）

［6］JEŽO.3DMapping and Localization Using Leveled Map Accelerated ICP［C］∥Bruyninckx H，Prˇeucˇil L，Kulich M.European Robotics Symposium 2008.Berlin Heidelberg：Springer，2008：343－353.

［7］MANDOW A，MARTÍNEZ J L，REINA A J，et al.Fast Range－Independent Spherical Subsampling of 3DLaser Scanner Points and Data Reduction Performance Evaluation for Scene Registration［J］.Pattern Recognition Letters，2010，31（11）：1239－1250.）

［8］KENNER R，PHILLIPS M，DANIOTH C，et al.Investigation of Rock and Ice Loss in a Recently Deglaciated Mountain Rock Wall Using Terrestrial Laser Scanning：Gemsstock，Swiss Alps［J］.Cold Regions Science and Technology，2011，67（3）：157－164.

［9］BRENNER C，DOLD C，RIPPERDA N.Coarse Orientation of Terrestrial Laser Scans in Urban Environments［J］.ISPRS Journal of Photogrammetry ＆ Remote Sensing，2008，63：4－18.

［10］ZHAO Xu，ZHOU Keqin，YAN Li，et al.3DReconstruction Method for Large Scale Relic Landscape from Laser Point Cloud［J］.Geomatics and Information Science of Wuhan University，2008，33（7）：684－687.（赵煦，周克勤，闫利，等.基于激光点云的大型文物景观三维重建方法［J］.武汉大学学报：信息科学版，2008，33（7）：684－687.）

［11］BESL P J，MCKAY N D.A Method for Registration of 3－D Shapes［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（2）：239－256.

［12］BORNAZ L，LINGUA A，RINAUDO F.A New Software for the Automatic Registration of 3DDigital Models Acquired Using Laser Scanner Devices［C］∥CIPA WG 6 International Workshop on Scanning for Cultural Heritage Recording，Corfu：［s.n.］，2002：52－57.

［13］PARK S Y.A Fast Point－to－Tangent Plane Technique for Multi－view Registration［C］∥Fourth International Conference on 3－D Digital Imaging and Modeling，2003.3DIM 2003，Banff，Alta：IEEE，2003：276－283.

［14］ZHENG Dehua，YUE Dongjie，YUE Jianping.Geometric Feature Constraint Based Algorithm for Building Scanning Point Cloud Registration［J］.Acta Geodaetica et Cartographica Sinica，2008，37（4）：464－468.（郑德华，岳东杰，岳建平.基于几何特征约束的建筑物点云配准算法［J］.测绘学报，2008，37（4）：464－468.）

［15］ZHANG Jianqing，ZHAI Ruifang，ZHENG Shunyi.Automatic Seamless Registration of 3DMultiple Range Views［J］.Geomatics and Information Science of Wuhan University，2007，32（2）：100－103.（张剑清，翟瑞芳，郑顺义.激光扫描多三维视图的全自动无缝镶嵌［J］.武汉大学学报：信息科学版，2007，32（2）：100－103.）

［16］MECHELKE K，KERSTEN T P，LINDSTAEDT M.Comparative Investigations into the Accuracy Behaviour of the New Generation of Terrestrial Laser Scanning Systems［J］.Optical 3－D Measurement Techniques VIII，2007，1：319－327.

［17］BOEHLER W，VICENT M B，MARBS A.Investigating Laser Scanner Accuracy［J］.The International Archives of the Photogrammetry，Remote Sensing and Spatial Information Sciences，2003，34（5）：696－701.

［18］HODGE R A.Using Simulated Terrestrial Laser Scanning to Analyse Errors in High－resolution Scan Data of Irregular Surfaces［J］.ISPRS Journal of Photogrammetry and Remote Sensing，2010，65（2）：227－240.

［19］JOCHEM A HÖFLE B，WICHMANN V，et al.Area－Wide Roof Plane Segmentation in Airborne LiDAR Point Clouds［J］.Computers，Environment and Urban Systems，2012，36（1）：54－64.）

［20］SANKARANARAYANAN J，SAMET H，VARSHNEY A.A Fast All Nearest Neighbor Algorithm for Applications Involving Large Point－Clouds［J］.Computers ＆ Graphics，2007，31（2）：157－174.

［21］MA H C WANG Z Y.Distributed Data Organization and Parallel Data Retrieval Methods for Huge Laser Scanner Point Clouds［J］.Computers ＆ Geosciences，2011，37（2）：193－201.

［22］FLÖRY S，HOFER M.Surface Fitting and Registration of Point Clouds Using Approximations of the Unsigned Distance Function［J］.Computer Aided Geometric Design，2010，27（1）：60－77.

［23］YAO Jili.SARC Model of Three－dimensional Coordinate Transformation［J］.Geomatics and Information Science of Wuhan University，2005，30（9）：825－828.（姚吉利.三维坐标转换的静态滤波模型［J］.武汉大学学报：信息科学版，2005，30（9）：825－828.）

［24］YAO Jili.Rigorous Formula for Direct Calculating Parameter in 3DTransformation［J］.Bulletin of Surveying and Mapping，2006（5）：7－10.（姚吉利.3维坐标转换参数直接计算的严密公式［J］.测绘通报，2006（5）：7－10.）

［25］YAO Jili，HAN Baomin，YANG Yuanxi.Applications of Lodrigues Matrix in 3DCoordinate Transformation［J］.Geomatics and Information Science of Wuhan University，2006，31（12）：1094－1096.（姚吉利，韩保民，杨元喜.罗德里格矩阵在三维坐标转换严密解算中的应用［J］.武汉大学学报：信息科学版，2006，31（12）：1094－1096.）

［26］PU Shi，LI Jingwei，GUO Siqing.Registration of Terrestrial Laser Point Clouds by Fusing Semantic Features and GPS Positions［J］.Acta Geodaetica et Cartographica Sinica，2014，43（5）：545－550.（浦石，李京伟，郭四清.融合语义特征与GPS位置的地面激光点云拼接方法［J］.测绘学报，2014，43（5）：545－550.）

［27］YAO Jili，JIA Xiangyang，MA Ning，et al.Auto－registration for Terrestrial Laser Scanning Multi－stations Point Clouds with Bundle Block Adjustment Method［J］.Acta Geodaetica et Cartographica Sinica，2014，43（7）：711－716.（姚吉利，贾象阳，马宁，等.光束法区域网平差的地面激光扫描多站点云自动定向方法［J］.测绘学报，2014，43（7）：711－716.）

［28］YAO Jili，JIA Xiangyang，MA Ning，et al.Auto－Orientation of Multi－stations TLS Point Clouds with Bundle Block Adjustment［J］.Acta Geodaetica et Cartographica Sinica，2014，43（8）：835－841.（姚吉利，贾象阳，马宁，等.地面激光扫描多站点云整体定向平差模型［J］.测绘学报，2014，43（8）：835－841.）