道路冲刷机构动力学分析、动应力分析及仿真

（武汉工程大学 机电工程学院，武汉 430205）

0 引言

随着我国经济的发展对道路要求越来越高，而路面基层中的半刚性材料抗冲刷性能的不足是道路损坏的重要因素之一，因此研制一台能够良好的模拟路面基层实际工况的设备来检测半刚性材料的抗冲刷性能显得尤为重要。

国外在路面基层冲刷作用这方面作了较多的研究工作。美国的蒂阿（Tia，1986），邓普西叩（Dempsey，1982），冯威吉克（Van Wijk，1985，1989），亨森（Hansen，1991）等人采用观察和现场试验方法[1]，对道路脱空区滞留水的压力和流速进行研究。法国道路部门利用旋转刷盒振动台试验装置开展道路冲刷试验[2]等等。我国的沙爱民、郝培文就半刚性基层材料抗冲刷性能探究了一些实验方法[3,4]，胡立群[4]、关增智[5]、朱唐亮[6]等人就半刚性基层材料抗冲刷性能也纷纷做出了自己的贡献，另外沙爱民教授开发了用于道路基层材料的抗冲刷性能试验机，对国外的冲刷设备有了较好的改进，但是压头直接作用在试件表面,与实际中荷载是作用面层表面和细集料被挤出或者被吸出的情况不符，而且实验平台较大，推广不易，因此设计研制了一台与实际工况较为符合且实验平台较小的设备用以检测半刚性材料的抗冲刷性能。

结合机械设计软件SOLIDWORKS的帮助，新型道路冲刷模拟实验设备主体如图1所示。

图1 新型道路冲刷机构主体三维模型

1 理论分析

1.1 驱动力矩分析

道路冲刷机构的动力学分析主要研究冲刷机构在动载荷作用下的驱动力矩的变化情况。

道路冲刷机构的执行部分可以简化为如图2所示的对心曲柄滑块装置，其中驱动力矩大小为M，方向为顺时针，曲柄OA的长度是偏心轴的偏心位移，长度为r，转速为n，曲柄AB的长度为LAB。当曲柄OA越过水平位置时，压头将受到由于压头向下运动挤压橡胶垫产生的方向竖直向上的变形力。

假设橡胶变形程度为小变形，在小变形范围内，橡胶垫可视为一线性弹性元件，具有大小为K的刚度系数，大小为E的弹性模量。

已知橡胶垫直径为R，厚度为L，工作过程中需要在橡胶垫上产生最大为P的压力，因此可以得到作用在压头上的力Fp的大小为：

由于当橡胶垫压缩量为r时，橡胶垫将产生大小为Fp的变形力，因此橡胶垫的弹性模量E至少为：

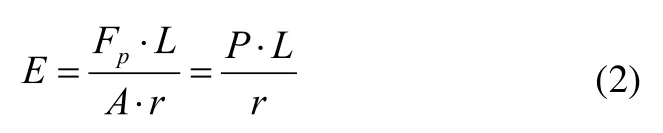
刚度系数K为：

如图2所示，假设曲柄运动到图示位置时，系统处于平衡状态。因此，曲柄OA，曲柄AB，压头B的受力情况如图3～图5所示，压头受到冲压阻力F、导轨约束力FN以及连杆的作用力FB作用。

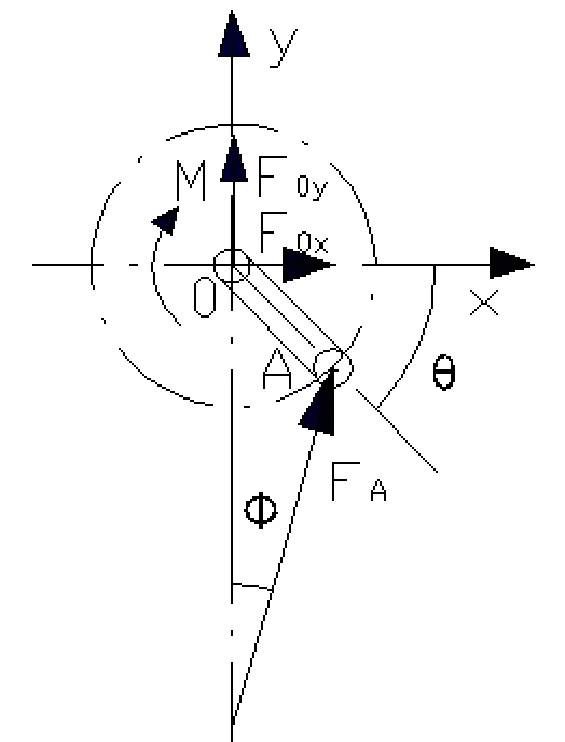
图2 平衡位置

图3 曲柄OA受力示意

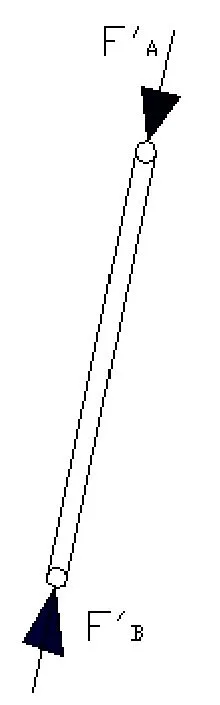
图4 曲柄AB受力示意

图5 压头B受力示意

此时曲柄OA转动角度为θ，连杆与直线OB间的夹角为Φ，因此橡胶压缩量为：

故冲压阻力F大小为：

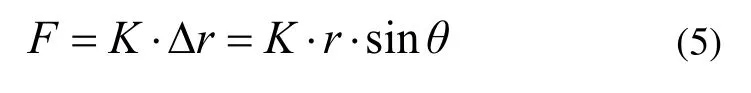
由经典力学分析，对于图3，有：

对于图4，有：

其中F'A和F'B分别为FA和FB的反作用力。

对于图5，有：

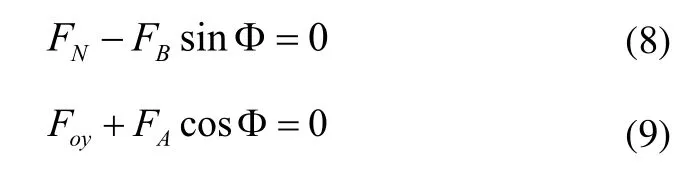
联立式(1)～式(9)，可得知，驱动力矩M的表达式为：

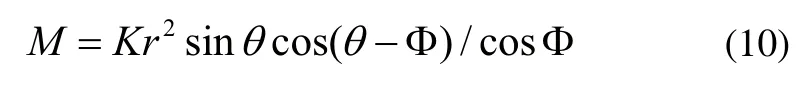
式(10)即为冲刷机构在动载荷作用下驱动力矩的变化情况，其中如图2所示从曲柄OA越过右边水平位置向下运动至脱离左边水平位置的范围内。

由已知工程实际数据，R=150mm，r=2mm，n=600r/min，LAB=45mm，P=0.7MPa，L=22mm。

由于：

由Φ值的变化情况，因此驱动力矩M的表达式可以简化为：

上式当且仅当Φ值变化较小时成立。

因此，当sin2θ=1即θ=45°时，曲柄OA上的驱动扭矩M最大为：

1.2 关键零部件（偏心轴）动应力分析

偏心轴是冲刷机构中的关键零部件，材料为45号钢，由于冲刷机构的压头部分整个都悬挂在偏心轴的偏心段，而且工程要求冲刷机构压头冲击频率为10Hz，因此，在高速冲击下，有必要校核偏心轴的动强度，确保偏心轴在工作过程中能够安全稳定的运行，避免发生断轴的危险。

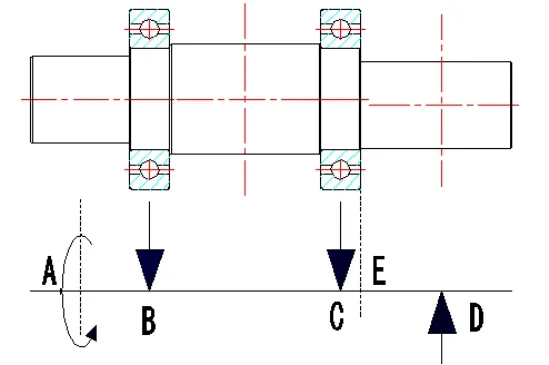
图6 偏心轴受力图

图6各段间距离分别为：

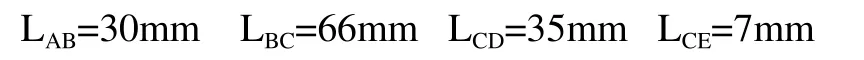
由之前的理论动力学分析可知，在运动过程中，偏心轴A处受到的驱动扭矩最大为：T=12.37N·m，在偏心轴D出受到阻力Fp，其中Fpmax=12370N。因此偏心轴在运动过程中的受力情形属于弯扭组合，下面仅以最大动载荷Fpmax来计算轴承的约束力。

因为偏心轴只受到径向约束力，设轴承在B、C处施加的约束力分别为F1，F2。

由平衡方程：

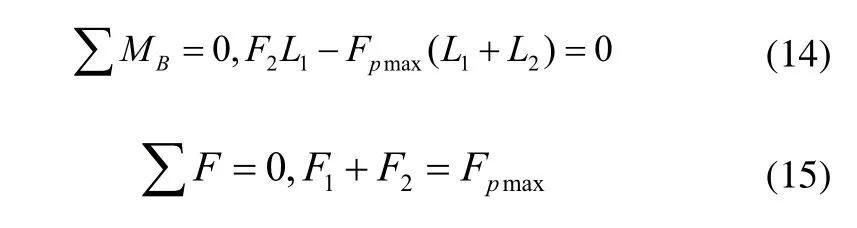
代入数据可得：

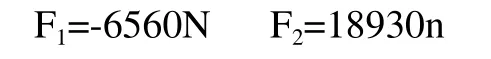
因此，可以得知，在F2所在的右轴承中心平面上，弯矩最大值为：

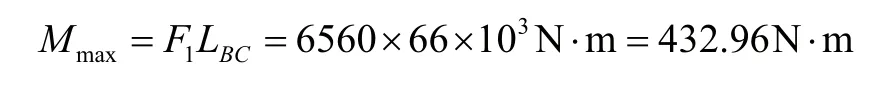
由于在偏心轴属于阶梯轴，在右轴承端面E处存在尺寸突变，而相距7mm的位置弯矩有最大值，因此需要确定突变截面上（即E处）上的弯矩以及强度。

突变截面E处：

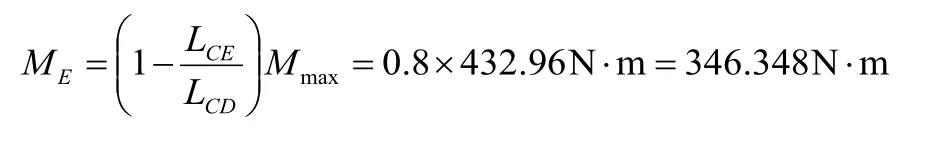
由于偏心轴受到的载荷类型属于动载荷，需要确定偏心轴的动荷系数Kd。

理论上，动荷系数Kd的表达式为：

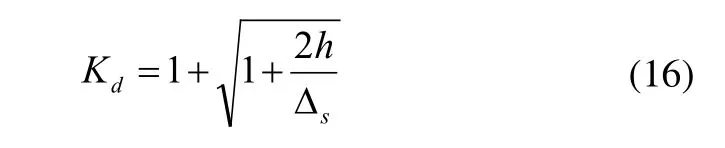
在这里，由机构的运动分析可知，当偏心轴偏心段转动到最下方时受到的载荷最大，而载荷次最大变化到载荷最大的时间段Δt（Δt→0）内，偏心轴偏心段最下端与施力点的距离为Δh（Δh→0），因此可以得到，h=0，意即可以视为突加载荷。

由上分析，动荷系数为：

动载荷时的应力为：

由材料力学知识，有：

其中已知dC=35mm，dD=30mm，因此计算可得：

由上分析，可以知道突变截面E上的正应力和切应力均大于最大弯矩C处。所以，在突变截面E上，由畸变能密度准则，有：

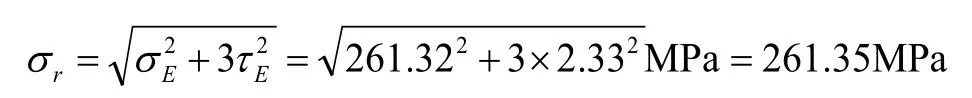
2 仿真实现

在SOLIDWORKS中经过建模→装配→去除冗余约束→修改部件材料属性→设置引力→添加驱动电机→添加力等一系列步骤后，便能够进行冲刷机构的动力学仿真和动应力仿真。

零部件装配完成后，通常都存在冗余约束，所谓冗余约束，即对配合机构上的某一指定的自由度添加了多余的约束，而当装配模型存在冗余约束时，SOLIDWOKS在求解时将会产生两种错误，一是求解时仿真了错误的零件载荷传递路线；二是错误的力的计算。为了避免后续动力学分析和动应力分析结果的失真，必须确保整个装配件的冗余约束数目为零。

去除冗余约束后，由SOLIDWORKS中自带的计算自由度功能，可以知道冲刷机构模型的冗余约束为零。

2.1 动力学仿真

设置完毕并且SOLIDWORKS运算完成后，可以得如图7所示的压头的位移变化图像、如图8所示的压头的加速度变化图像，以及如图9所示的驱动力矩的变化图像。

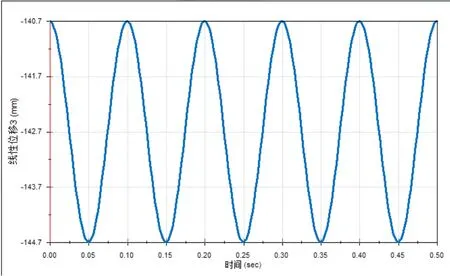
图7 压头的位移

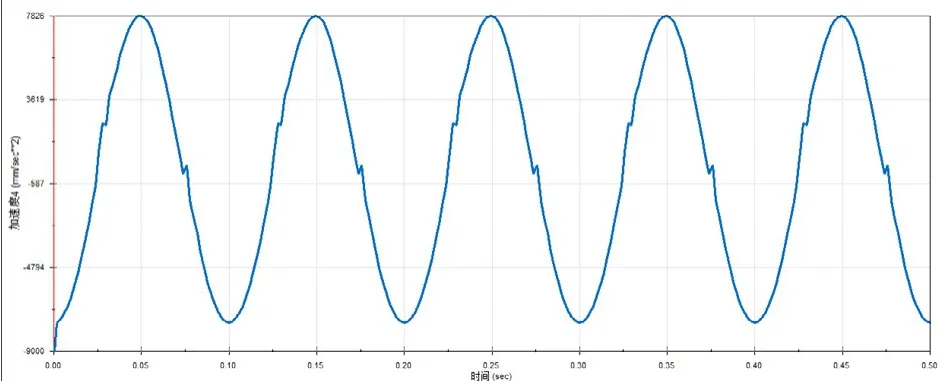
图8 压头的加速度

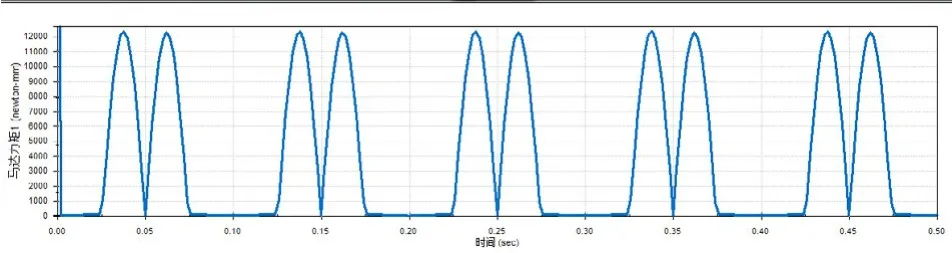
图9 驱动力矩

由图7压头的位移图像，可以得到压头运动的总位移为4mm，并且周期为0.1s，符合实际工程要求。

通过对图8压头的加速度图像的分析，可以知道，压头在运动过程中的最大加速度为7.826m/s2，在运动过程中由于受到突加负载和惯性的影响，因此存在短暂的冲击，但对整个运动过程而言，这种冲击所带来影响微乎其微。

从图9驱动力矩图像中可知，驱动力矩最大值为12483N·mm，即12.483N·m，此时θ=43°，这与之前的理论计算结果12.37N·m和θ=45°相比，误差分别为1%和4.4%，因此仿真结果可信度高，并且证明了在SOLIDWORKS中建立的装配模型必须为零冗余约束装配模型的必要性。

2.2 关键零件的动强度仿真

SOLIDWORKS中的Simulation插件相比于其他有限元分析软件而言，特点在于能够直接调用SOLIDWORKS Motion的运算结果，然后对所需要进行强度仿真分析的零件单独打开进行分析即可。

在进行动强度仿真分析时，主要步骤是：1）在动力学分析过程中指定零件载荷平面；2）导入动力学计算结果到Simulation中；3）设定零件材料属性；4）划分网格；5）运算求解；6）导出运算结果。

Simulation中设置网格密度为5mm，网格参数选择基于曲率的网格，高级设计中草稿品质网格不勾选。

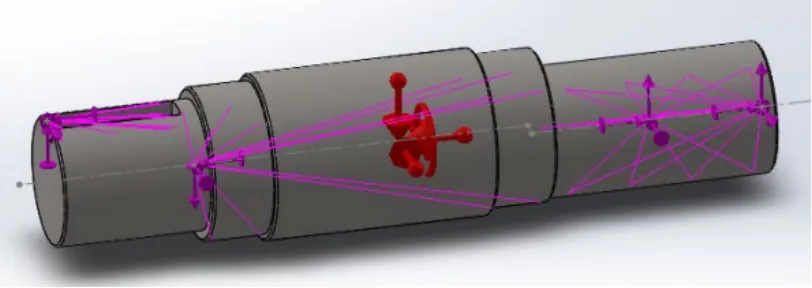
图10 偏心轴的载荷平面

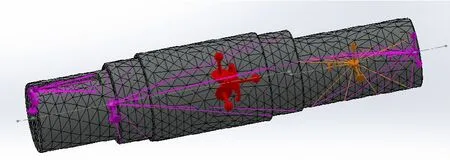
图11 偏心轴网格划分效果

在0.1s内，SOLIDOWKRS Simulation划分了50个等时段不同载荷的计算情形来求解计算。设置并运算完毕后，偏心轴的动应力变化如图12所示，变形量曲线如图13所示。

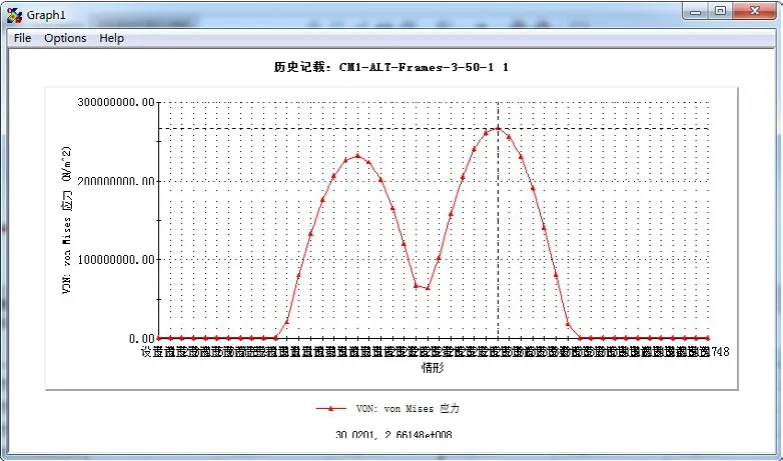
图12 动应力变化曲线

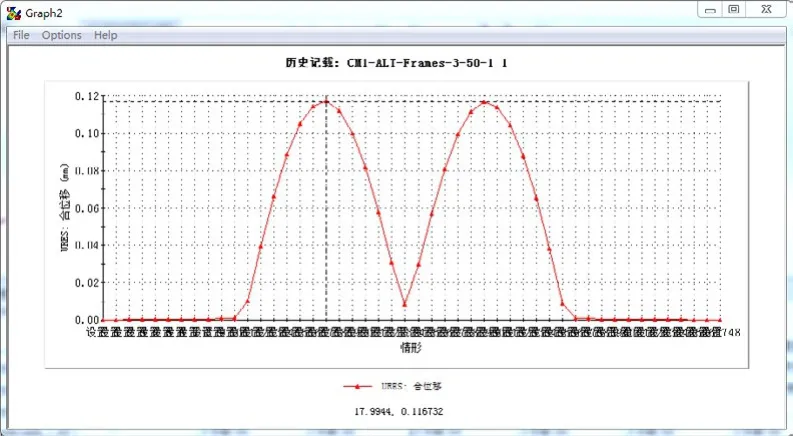
图13 变形量变化曲线图

从图12、图13可以看出，情形30出存在最大应力以及最大变形。因此调取情形30偏心轴的动应力分布图和变形量图，效果如图14、图15所示。

图14 偏心轴计算情形30处的应力分布

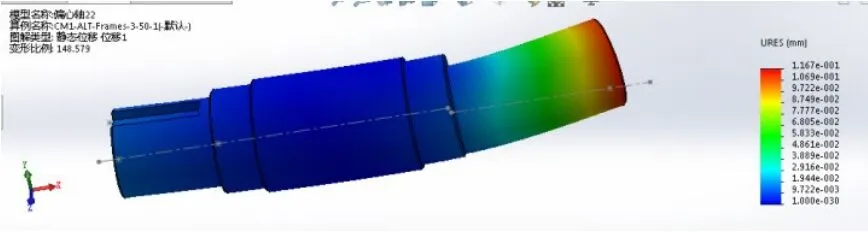
图15 偏心轴计算情形30处的变形分布

从图14中可以看出，偏心轴工作中的最大应力为266.8MPa，与之前理论计算值261.35MPa相比，误差为2.09%，因此结果可信度高，由图15可得偏心轴最大变形量为0.116mm。因偏心轴材料为45号钢，故屈服应力为355MPa，因此偏心轴在运动过程中，安全系数最小为：355/266.8=1.33，最大应力小于屈服应力，所以偏心轴能够安全稳定地运行。

3 结论

本论文从理论和仿真两方面具体阐述了冲刷机构在动载荷作用下的扭矩变化情况，以及对于关键零件即偏心轴在动载荷作用下的动应力变化。基于SOLIDWORKS的动力学仿真分析结果和偏心轴的动应力仿真分析结果对冲刷机构的实际运行状况具有一定的参考价值，其中动力学仿真的驱动力矩仿真结果和动应力仿真分析结果分别与理论分析结果相比，误差仅为1%和2.09%，可信度高。

通过利用SOLIDWORKS进行虚拟样机研制并进行相关的分析计算，区别于ADAMS和ANSYS，SOLIDWORKS提供了一种全新的工业机械虚拟样机研制方法，尤其是当模型较为复杂，理论建模困难时，在确保装配为零冗余约束的情况下，SOLIDWORKS能够较好的完成仿真工作，而且整个操作过程较ADAMS和ANSYS相比要简单，顺畅，能够为设计人员节省大量的精力以及时间。