真空炉炉门混合建模方法研究与检验
2018-07-21
(中南大学 机电工程学院,长沙 410083)
0 引言
作为一种真空热处理设备,真空炉具有无氧化脱碳,高效节能等特点,被广泛应用于航空、航天、兵工、核工业等领域零部件生产制造。炉门组件是真空炉关键组件,用于实现炉门与炉体的密封配合。大型真空炉炉门结构复杂,尺寸变化大,且载荷工况恶劣,按常规方法进行设计分析较为困难。目前多采用有限元法进行设计分析[1,2],原晓刚等[3]采用壳单元研究了外压圆柱壳体容器稳定性问题。壳单元的使用具有一定局限性,无法在危险截面进行厚度方向的应力线性化分析,且厚度较大的局部结构处,无法使用壳单元进行建模。李志刚等[4]采用全实体建模的方法,研究了水下分离器结构总体塑性变形。而大型设备FEM建模时,采用全实体单元会导致网格数量过多,计算资源消耗大。当设备结构复杂时,还会给模型的建立带来较大困难。
针对上述问题,本文以某型号卧式真空炉炉门组件为研究载体,结合其实体、薄壁组合的结构特点,采用体-壳组合模型、全实体模型两种不同建模方法对其进行仿真分析。体-壳组合模型建立时,门体法兰与内、外封头连接区域附近的封头及法兰采用实体单元建模,其余部分采用壳单元建模。通过此种方式建立模型,有利于模拟仿真封头与法兰连接处应力集中等真实情况。但体、壳单元节点自由度不同[5],建模时需解决体-壳单元在连接界面处节点自由度匹配问题。谢最伟等[6,7]运用刚度叠加法和MPC法对体-壳组合模型进行了仿真分析,并且与全实体单元模型进行对比,得到较为理想的模拟结果,但并未进行相应的实验验证。
本文将分别采用体-壳组合模型与全实体模型两种不同建模方法研究真空炉炉门应力状态分布。同时利用电测法进行应力测试实验。将结果进行对比分析,以验证体-壳单元组合建模方法在此类真空炉炉门仿真分析上的可行性和精确性。
1 有限元仿真分析
1.1 几何模型及材料参数
本文所研究真空炉炉门由内、外封头、门体法兰等焊接而成。炉门内、外封头为JB/T4746EHA型碟形封头,公称直径分别为φ1200mm、φ1300mm,壁厚分别为16mm、8mm,真空炉常规工况下,在炉门内、外封头之间通入绝对压力0.25MPa冷却水后,将进行抽真空处理,炉内极限真空度为5Pa。真空炉炉门组件几何模型如图1所示。

图1 几何模型图
炉门内、外封头所用制造材料为Q235B,门体法兰为Q345。材料力学性能参数[8,9]如表1所示,ρ为材料密度,E为弹性模量,σ0.2为屈服强度,σb为强度极限,μ为泊松比。
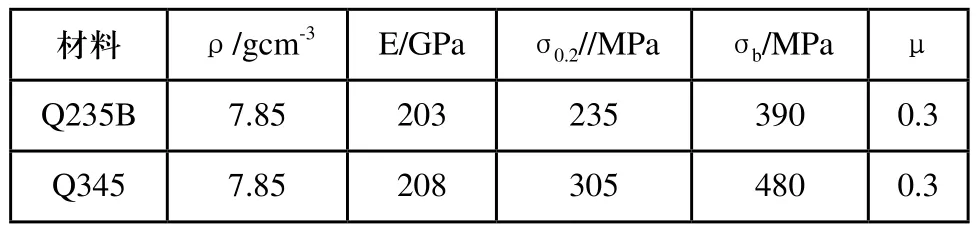
表1 材料参数
1.2 有限元模型建立
为便于对比分析,本文建立以下两种仿真模型:
1)体-壳混合单元模型,即采用壳单元与实体单元进行组合建模;
实体单元与壳单元在连接处易出现应力情况失真,为保证求解精度,体-壳连接处应避开应力集中部位。为避免连接处对关心区域应力场干扰,封头与法兰连接区域及法兰采用solid186单元建模,其余部分采用shell181。焊接处依据焊缝等强度原则,将焊缝结构简化为倒角。如图2所示。由于炉门结构与载荷分布具有对称性,因此运用workbench的symmetry功能建立1/2模型。

图2 体-壳混合单元模型
2)全实体单元模型,即整个炉门全采用实体单元建模。
为保证模型的统一性,结合门体法兰结构特点,对其进行slice切分后,同样采用实体单元solid186进行网格划分,建立1/2模型,如图3所示,运用slice功能进行切分后可获得十分规整及较高质量网格。两种分析模型具体参数对比如表2所示。
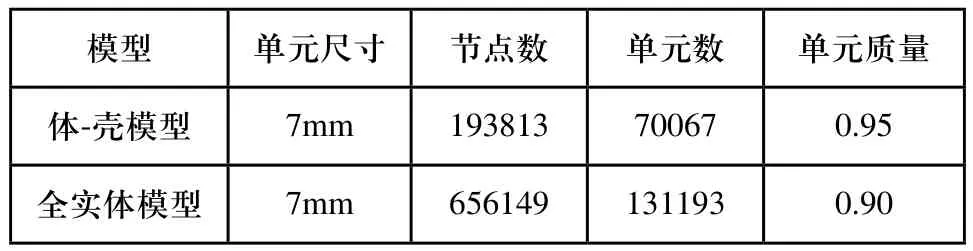
表2 网格参数

图3 全实体模型
1.3 体-壳混合单元模型连接处理
由于体、壳单元节点自由度不同,采用共节点法处理两种单元的连续将不可避免地导致交界处应力情况失真,而多点约束方程法不需要连接处的节点一一对应,即可将不同类型单元进行耦合连接,操作十分便利,同时具有较高的计算精度[10]。为保证求解精度,采用多点约束(MPC)法连接体、壳单元。MPC法是通过一个节点某几个自由度为标准值,建立指定节点的自由度与标准值的约束关系,从而实现体-壳单元的耦合。其一般关系式如下:
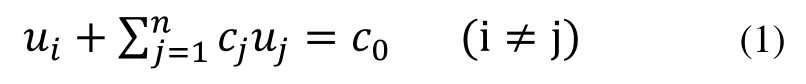
式中:ui为从自由度;cj为权系数;uj为主自由度;c0为常数项;i为从节点某自由度下标;j为主节点某自由度下标。
1.4 仿真结果及对比
根据真空炉炉门真实载荷工况,两种模型水冷夹套内部施加内压0.25MPa,炉门外表面施加0.1MPa外压,对炉底部表面进行固定约束。两种模型整体位移云图如图4所示。从图中可以很直观地发现,体-壳模型变形趋势与全实体模型基本保持一致。以全实体模型等效位移数值为基准,体-壳模型最大总变形相对误差为1.78%。

图4 总位移云图
图5为两种模型von-Mises等效应力云图。从图中可看到,两者等效应力最大值均出现在外封头内壁过度区域,其数值大小也基本相同。体-壳模型等效应力最大值为45.811Mpa,全实体模型为46.61Mpa,相对误差仅为1.71%。两种模型应力分布状态也基本一致。体-壳模型与全实体模型仿真结果基本一致,有着较高准确度。
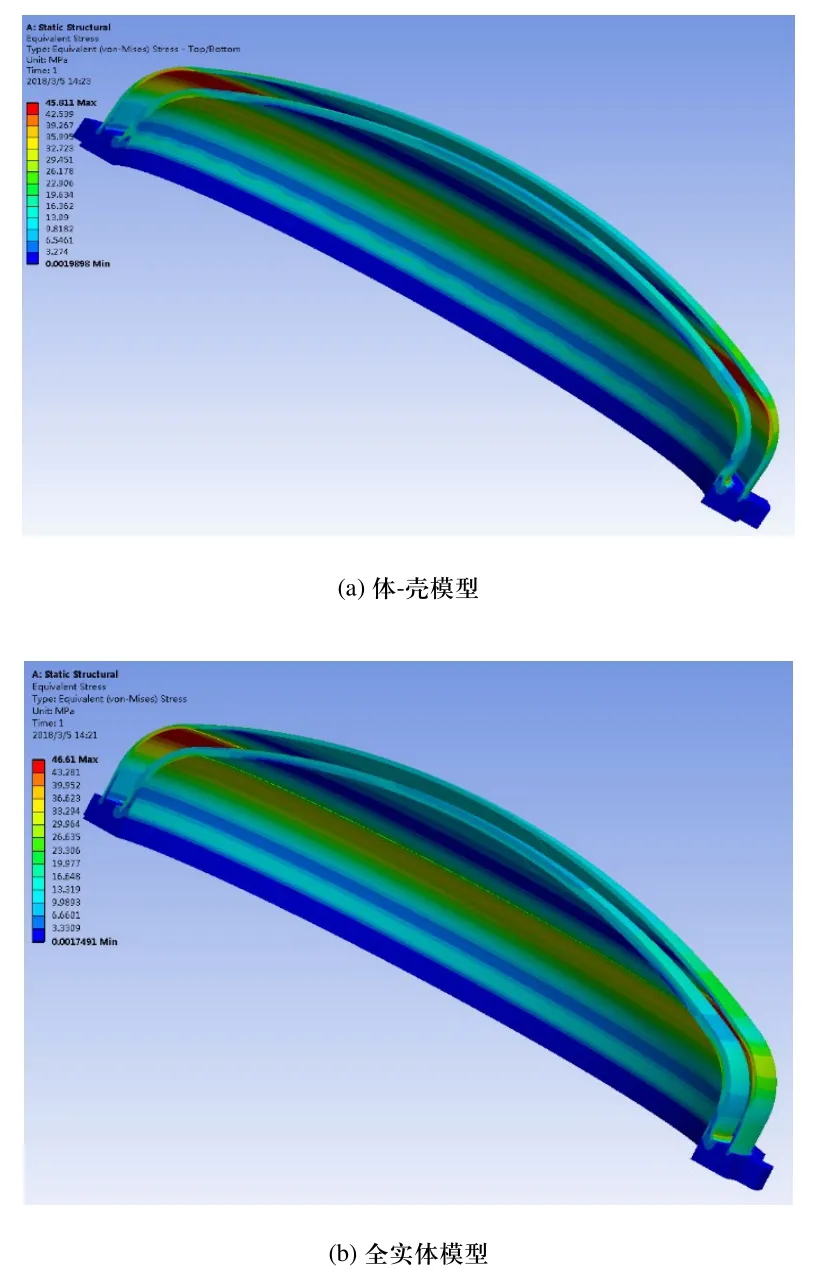
图5 von-Mises等效应力云图
2 试验验证
2.1 试验原理及装置
为验证不同有限元方法分析结果的准确性,本文采用电测法对真空炉炉门内壁进行应力测试实验。实验采样设备为DH5925动态信号分析仪,检测元件为BA120-3BA的直角双轴应变花。根据模型几何结构特点,于真空炉炉门内壁布置8个测试点。具体测点位置和实验现场图分别如图6、图7所示。

图6 测试点布置图

图7 测试现场图
采集各测点应变信号后,根据广义胡克定律可推导出内封头内壁表面应力σm、θ。

式中:εm为经向应变;εθ为周向应变;σm为经向应力;σθ为周向应力;μ为材料泊松比;E为材料弹性模量。
2.2 试验与有限元结果对比
将两种建模方法下的数值模拟结果与电测法得到的结果制成折线图,可直观地对比分析不同方法下炉门应力分布异同。由图8、图9可以观察到三种方法所得经向、周向应力趋势均十分一致。经向应力最大值出现在内封头与法兰焊接处,而最小值处在过度环中间区域。最大周向应力位于过度环与球壳连接处,而最小值出现在靠近内封头球面附近。应力值的波动与极值的产生是内封头直边与法兰焊接处、内封头过度环与直边、过度环与球壳等连接处边缘应力导致的。
体-壳混合单元模型中,经向、周向应力值在体-壳单元接触界面节点上均存在一定偏差,经向、周向应力最大相对误差在13%左右,节点应力值失真[11]。在分析连接处应力值时因以相邻节点平均应力进行代替。其他节点位置数值与实验值、全实体结果基本一致,经向、周向应力相对误差处在4%~10%之间。采用此种混合建模技术进行数值模拟相比全实体建模有着更高的计算效率,同时有着较高的计算精度。

图8 经向应力分布图

图9 周向应力分布图
3 结论
本文分别采用体-壳混合单元与全实体单元两种不同建模方法,对某型号真空炉炉门组件进行有限元分析,最后对比了有限元计算结果与实测结果,得出以下结论:
1)多点约束(MPC)法能较好处理体-壳模型中自由度匹配问题时。相对全实体模型,体-壳混合单元模型的节点数仅为全实体模型的1/3,有着更高的计算效率且建模更简便。两种模型的应力分布基本一致,最大von-Miss应力均位于封头内壁过度区域,相对误差仅为1.71%。
2)壳单元与体单元接触界面节点上,经向、周向应力值均存在一定偏差,经向、周向应力最大相对误差在13%左右,节点应力值失真。建模时需避免体-壳连接处建立在结构应力集中处或分析的重点区域,在分析连接处应力值时因以相邻节点平均应力进行代替。
3)对比分析表明,体-壳混合单元模型仿真结果与实测轴向、周向应力变化规律一致,且经向、周向应力最大相对误差均在13%左右,平均相对误差处在4%~10%之间,计算精度满足工程要求。体-壳混合建模方法具备壳单元计算效率高和实体单元计算精准度好的特点,为大型复杂真空炉设备仿真分析等工程问题提供了可行的参考方案。
